基于不連續脈寬調制永磁同步電機邊帶聲振響應數值預測

張黎明，邱子楨，陳 勇，成海全，武一民，張志金

(1.河北工業大學 天津市新能源汽車動力傳動與安全技術重點實驗室，天津 300130；2.艾迪捷信息科技（上海）有限公司，上海 200120）

當前，作為電驅動系統的關鍵部件，永磁同步電機因其寬調速范圍、高能量密度和高可靠性等優點，在電動汽車領域得到了廣泛的應用。電驅動系統的噪聲、振動與聲振粗糙度(Noise，Vibration &Harshness，NVH)對于整車系統的性能開發至關重要。與傳統內燃機汽車相比，由于缺少了發動機的掩蔽效應，永磁同步電機驅動系統所輻射的高頻聲振響應更為顯著[1]，逐漸成為整車與部件級NVH 性能開發與優化的研究熱點。

永磁同步電機逆變驅動系統通常采用空間矢量脈寬調制(Space Vector Pulse-width Modulation，SVPWM)策略，以實現較高的直流母線電壓利用率[2]。然而，由SVPWM所引入的高頻邊帶電流諧波主要集中在載波頻率及其整數倍頻附近，不僅對電驅動系統的聲振特性造成嚴重影響，而且還會輻射出刺耳的高頻電磁噪聲[3]。因此，在電驅動控制系統設計開發階段，對邊帶諧波成分進行快速、準確分析尤為重要，并且對邊帶聲振響應抑制優化大有裨益。

為了研究邊帶電流諧波對電磁力的影響規律，文獻[4]對PWM(Pulse Width Modulation，PWM)所引入的電流諧波特性進行了分析，并推導了相應的徑向電磁力解析模型。文獻[5-7]通過建立永磁同步電機邊帶諧波分量解析模型，揭示了徑向電磁力的時空分布規律。文獻[8]對比分析了SVPWM 內、外轉子永磁同步電機的邊帶電磁力頻譜分布，分析了不同極槽配合對邊帶電磁力的影響，為永磁同步電機的噪聲識別與優化提供了理論基礎。

為了研究脈寬調制技術對電機聲振響應的影響，文獻[9]研究了由逆變器驅動的感應電機電磁激勵與電磁輻射噪聲之間的關系，并對電流諧波與聲振響應進行了頻譜分析，結果表明電磁激勵與輻射電磁噪聲具有強相關性。文獻[10]研究了在線與離線脈寬調制技術的基本特征及其對電機電磁噪聲的影響，并通過變速工況實驗驗證了理論解析的準確性。文獻[11]采用聯合仿真的分析方法，研究了寬調速范圍內，逆變器電流諧波對弱磁調速與恒轉矩調速電機振動噪聲的影響，結合仿真結果與實測數據得出逆變器供電永磁同步電機的振動噪聲頻譜增量主要體現在載波頻率附近。文獻[12]分析了不同載波頻域的邊帶電流諧波與機械振動噪聲之間的關系，為永磁同步電機的聲振預測提供了理論依據。

上述有關電流諧波及聲振響應的研究均基于連續脈寬調制(Continuous Pulse-width Modulation，CPWM) 策略[13－14]，對于不連續脈寬調制(Discontinuous Pulse-width Modulation，DPWM)策略產生的邊帶諧波特征規律研究尚不完善。DPWM能夠顯著提高逆變效率，已經廣泛應用于高功率型電壓源逆變器中[15－16]，然而其產生的邊帶諧波成分更加豐富。為此，本文以一臺12 槽-10 極永磁同步電機為研究對象，對DPWM策略所引起的邊帶電流諧波及聲振響應進行了特征識別與分析，基于DPWM的空間矢量原理與實現方法，建立了“機-電-磁-控”多物理場協同仿真模型，通過Simulink &JMAG 仿真預測了DPWM 策略對邊帶電磁力以及高頻振動噪聲的影響，分析了邊帶電流諧波及徑向電磁力的頻譜特征，并基于模態疊加與完全積分法計算了實驗樣機的聲振響應。最后，通過搭建12槽-10極永磁同步樣機邊帶電流諧波與聲振響應實驗，對邊帶成分的頻譜特征進行分析，驗證了理論解析與協同仿真模型的準確性。

1 DPWM原理與實現方法

1.1 DPWM基本原理

作為典型的CPWM 策略，SVPWM 的工作原理是根據U所在扇區的空間位置，確定要輸出的基本空間電壓矢量[17]。圖1 為SVPWM 的電壓空間矢量扇區圖，以第一扇區為例，SVPWM的開關序列如圖2(a)所示。在一個載波周期內，SVPWM將有效空間矢量居中放置，兩個零矢量邊沿對稱放置，逆變器各相橋臂根據載波頻率不斷地進行開關切換。

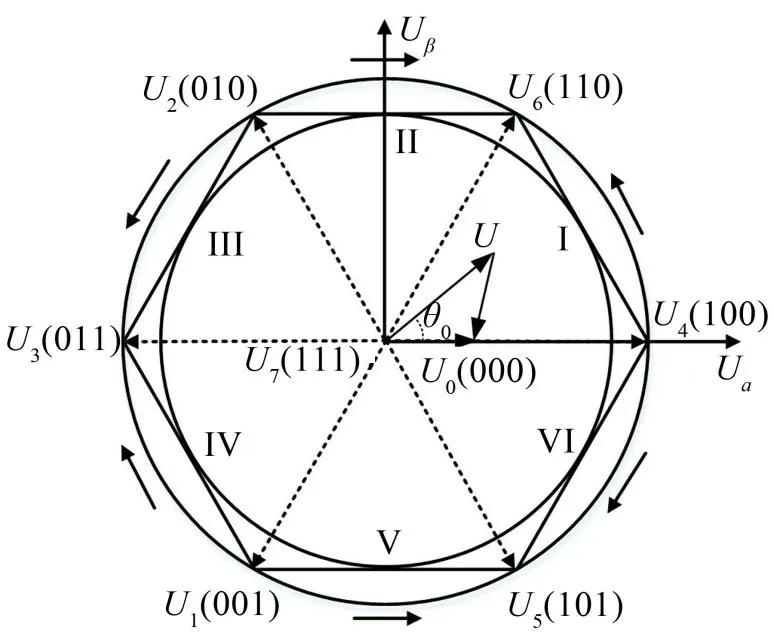
圖1 電壓空間矢量扇區圖

由CPWM 轉化為DPWM 最為直接的方式是將相鄰半個載波周期內的有效空間矢量彼此相連，通過摒棄一個零矢量使得A 相橋臂被鉗位在特定狀態[18]，如圖2(b)所示。通過不同的鉗位方式，可以得到6 種典型的DPWM 方案，即DPWMMIN、DPWMMAX、DPWM0、DPWM1、DPWM2 和DPWM3。

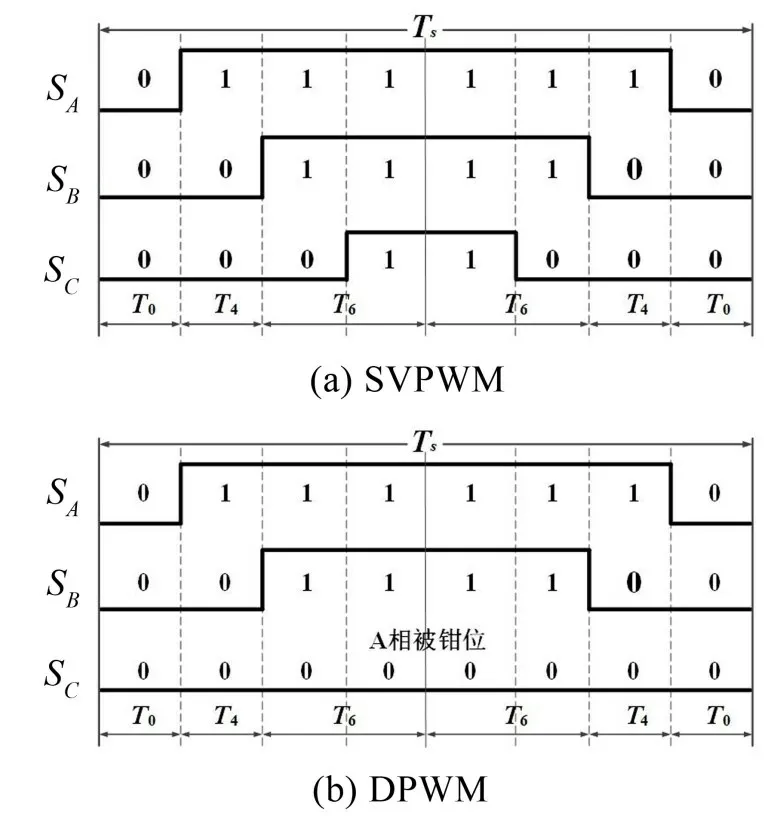
圖2 開關序列圖

1.2 DPWM實現方法

DPWM 的實現方式與SVPWM 類似，本質上都是通過對正弦調制波注入共模電壓信號的方式來實現，其共模電壓Uz計算公式為：

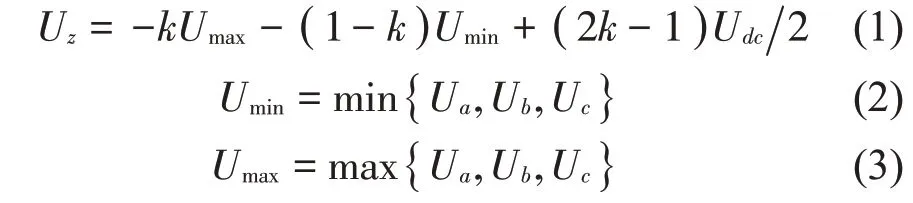
式中：Ua、Ub、Uc分別為三相相電壓；Umax、Umin分別為最大和最小輸出電壓；k為零矢量分配因子，取值為0或1，具體取值如表1所示。

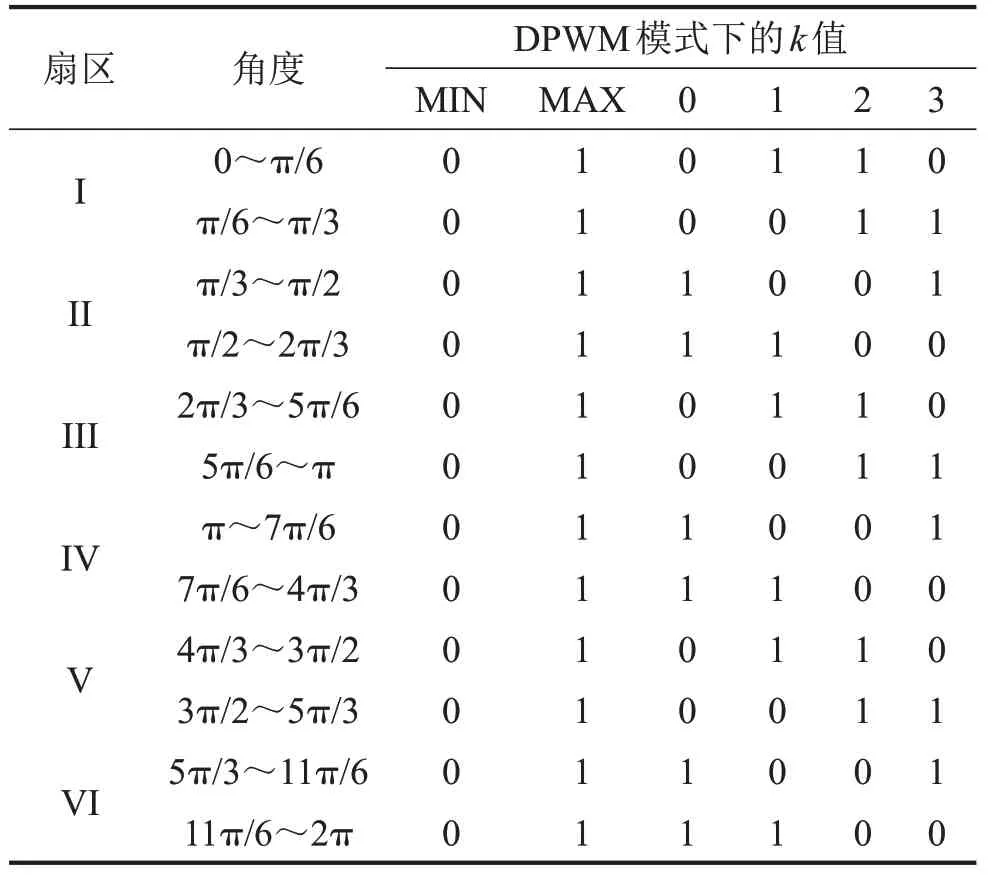
表1 不同DPWM模式下k的取值

(1)DPWMMIN和DPWMMAX

當整個開關周期滿足k值恒取1或0時，即僅有一個零矢量U7(1 1 1)或U0(0 0 0)與相鄰矢量進行組合，對應DPWMMIN和DPWMMAX模式，相應調制波波形如圖3所示。各相橋臂依次被鉗位到最大值或最小值，諧波性能較差。

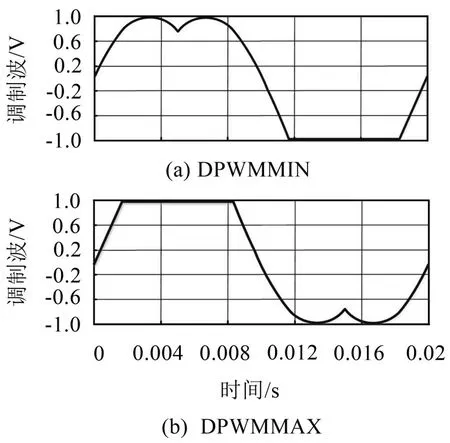
圖3 DPWMMIN與DPWMMAX調制波波形

(2)DPWM0和DPWM2

當k在第一、三、五扇區值取為0，第二、四、六扇區值取為1 時，對應DPWM0 模式，調制信號在鉗位區間內超前π/6輸出電壓峰值；反之則為DPWM2模式，相應調制波波形如圖4 所示。相比于DPWMMIN/MAX 策略，該類型下的調制波波形趨于對稱，諧波性能有所改善。

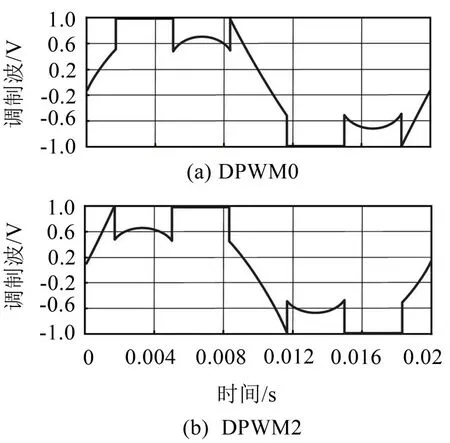
圖4 DPWM0與DPWM2調制波波形

(3)DPWM1和DPWM3

將原始的6 個扇區對稱劃分成12 個扇區，各扇區零矢量U7(111)或U0(000)交替進行工作，將k的取值在每個扇區內分別賦予0 和1 兩個值，即可獲得DPWM1和DPWM3模式，相應調制波波形如圖5所示。相比于其他類型DPWM，該類型下的調制波波形呈現對稱性，諧波性能最優。

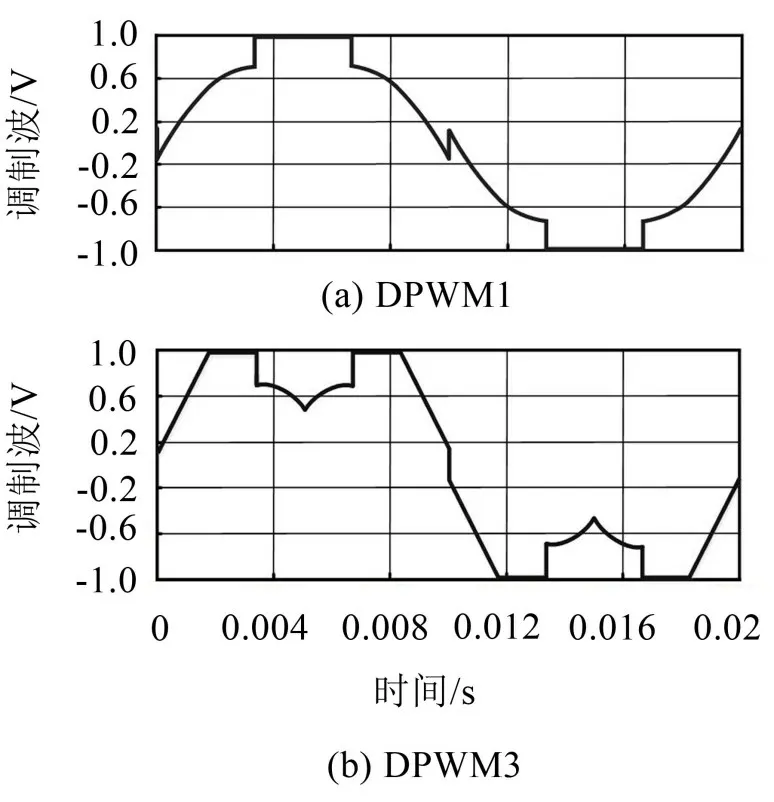
圖5 DPWM1與DPWM3調制波波形

2 邊帶電磁成分特征解析

2.1 徑向電磁力分析

在徑向磁通永磁同步電機中，作用在定子上的徑向電磁力是引起電機振動的主要因素。電磁力密度可由麥克斯韋應力張量法定義：

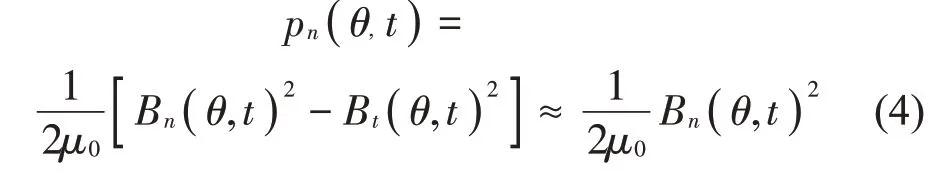
式中：Bn為徑向氣隙磁密，Bt為切向氣隙磁密；μ0為真空磁導率；由于Bn遠大于Bt，因此，忽略了切向氣隙磁密所產生的電磁力影響。

由于基波電樞場與諧波電樞場的幅值較小，為簡化計算，僅考慮永磁體磁場與諧波電樞場相互作用產生的邊帶電磁力[12]。因此，邊帶徑向電磁力密度可以表示為：

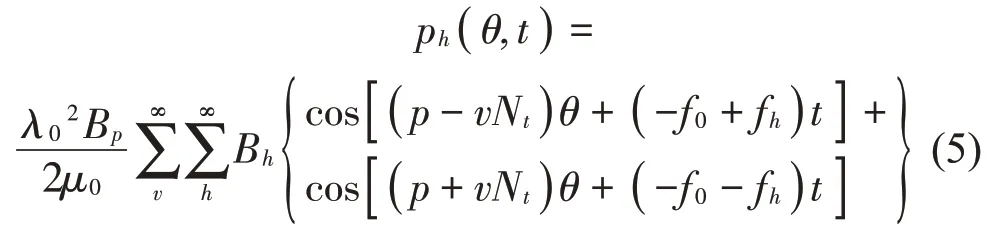
式中：Bp和Bh分別為永磁場磁密和諧波電樞場磁密。可以看出邊帶電磁力具有明顯的空間階次p±vNt和頻率次數f0±fh，其共同決定了邊帶諧波分量的分布特征。為進一步解析載波頻率附近的邊帶電磁力，還需對邊帶電流諧波進行分析。

2.2 考慮電流諧波的邊帶電磁力特征

DPWM 中的載波頻率可以表示為fc，調制波頻率可以表示為f0。邊帶電流諧波的解析表達式可以從轉子和定子坐標系中推導得出[5]。主要邊帶諧波的頻率分布可以表示為nfc±kf0，其中n和k由不同的奇偶校驗組成。以第一載波頻域為例，n為1。忽略幅值較小的高次諧波，DPWM中的邊帶電流諧波可以表示為：

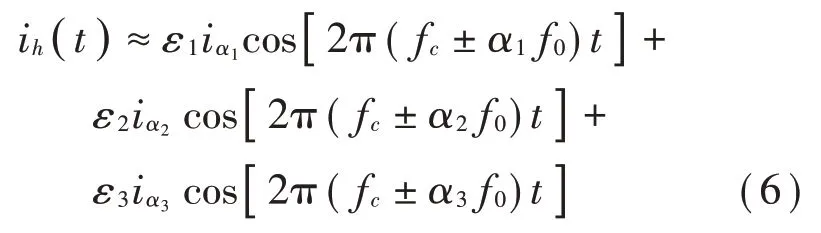
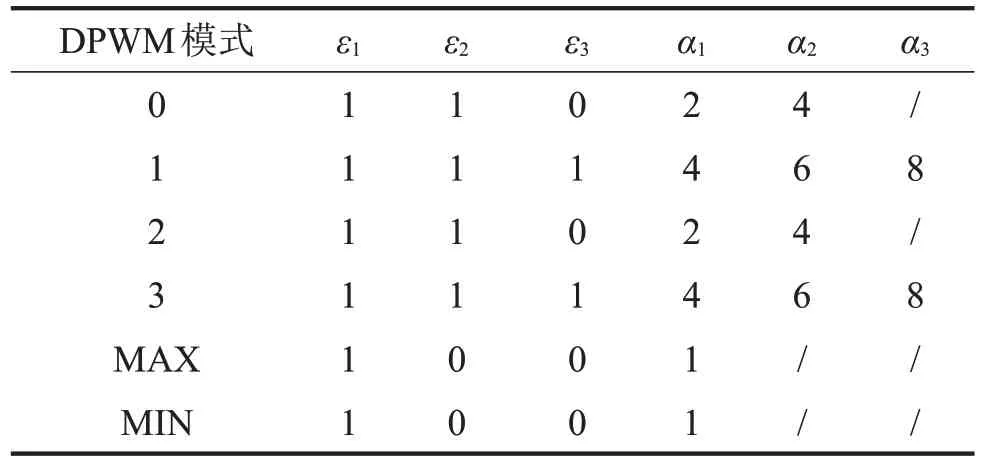
表2 不同DPWM模式對應的ε1、ε2、ε3、α1、α2、α3

邊帶電流諧波的幅值大小取決于電機的調制比與轉速[6]。不同DPWM模式下的電流諧波分布可根據式(6)與表2得出。

為分析邊帶電流諧波引起的電磁力，可將邊帶電流諧波分量轉化為對應特征頻率的磁通分量，通過計算得出邊帶電磁力。以特征頻率為fh=fc+2f0的電流諧波分量為例，其引起的邊帶電磁力特征頻率可表示為：

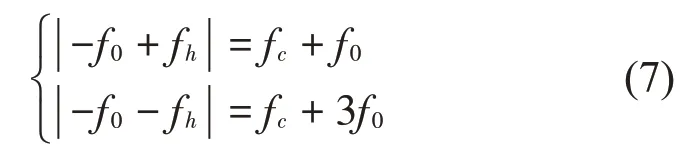
載波頻域附近邊帶電磁力的頻率分布如表3所示[19]。由此可進一步地對永磁同步電機聲振響應進行分析與識別。

表3 DPWM邊帶諧波分量頻率分析

3 電磁振動響應預測與驗證

3.1 邊帶電流諧波分量

本文以一臺12 槽10 極永磁同步電機為研究對象，分析了6種DPWM策略下電機的高頻聲振響應，電機主要參數如表4所示。

表4 永磁同步電機的主要參數

由于測試樣機的工作環境為500 r/min～1 500 r/min 和2 N?m～6 N?m，故選擇1 000 r/min 和4 N?m作為穩定工況，對6種DPWM的邊帶成分進行特征頻率識別與分析。圖6為1 000 r/min和4 N?m工況下6 種DPWM 策略的仿真與實測電流頻譜，載波頻率fc=8 000 Hz，電流基頻f0=83.33 Hz。為驗證電磁分析模型的準確性，對DPWM控制下的電機模型進行了仿真分析，并參照實驗數據對模型進行修正。從圖中可以看出，仿真結果相對實測數據幅值略低，但頻率特征基本吻合且與上述理論分析一致，驗證了電磁解析模型的準確性。

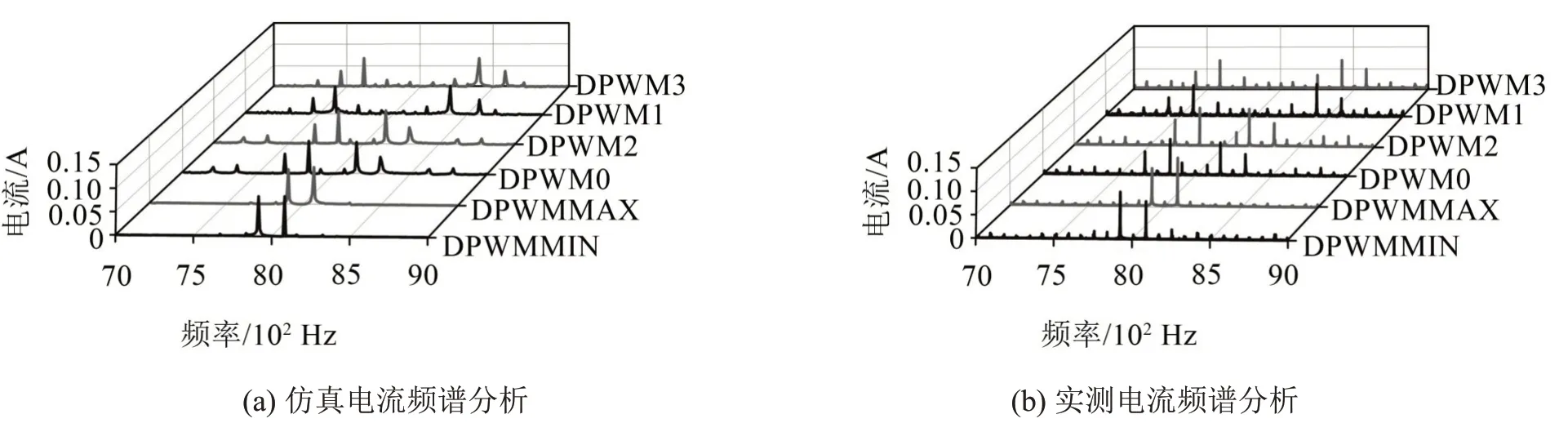
圖6 DPWM邊帶電流諧波頻譜分析

同一類型、不同模式的DPWM具有相似的頻率特征。DPWMMIN與DPWMMAX主要邊帶分量集中在中心頻率fc附近，位于fc±f0處。對于DPWM0與DPWM2，主要邊帶分量對應的特征頻率為fc±2f0和fc±4f0。DPWM1 與DPWM3 的主要邊帶分量距中心頻率fc較遠，位于fc±5f0和fc±7f0處。

3.2 邊帶電磁力有限元分析

通過有限元計算，可以得出1 000 r/min 和4 N?m工況下電機的徑向電磁力密度。分解得到邊帶電磁力頻譜如圖7 所示。圖7(a)為電機在DPWMMIN與DPWMMAX策略下的邊帶電磁力頻譜，從圖中可以看出，邊帶電磁力主要集中在中心頻率fc與fc±2f0。對于圖7(b)中的DPWM0與DPWM2，其主要邊帶成分特征頻率為fc±f0、fc±3f0和fc±5f0。圖7(c)中DPWM1與DPWM3主要邊帶成分位于fc±4f0、fc±6f0和fc±8f0。圖7 中所示的邊帶電磁力特征頻率與表3 中的結論相符，驗證了邊帶電磁力理論分析的準確性。

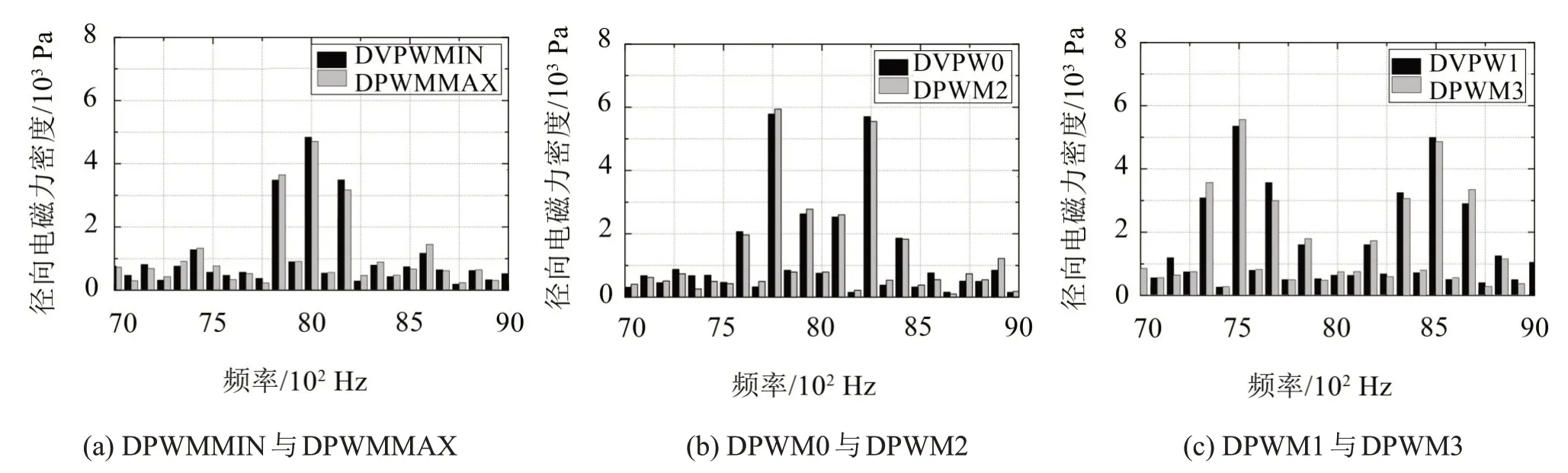
圖7 邊帶電磁力頻譜分析

3.3 模態分析

在JMAG-Designer中進行有限元分析以獲取樣機的模態參數。由于電磁力沿軸向幾乎均勻分布，因此周向模態對振動的貢獻量最大。為驗證有限元模型的準確性，本文采用移動力錘法進行了模態實驗。實驗過程中，采用彈力繩將樣機進行懸掛，同時放置了5個加速度傳感器以獲取殼體表面的振動響應。表5 列出了實測與仿真的模態振型及頻率，并將仿真結果中的前端蓋隱藏，以此來更加直觀地體現各階振型。結果表明，實測與仿真相對誤差均在5%以內，表明了有限元模型的準確性。

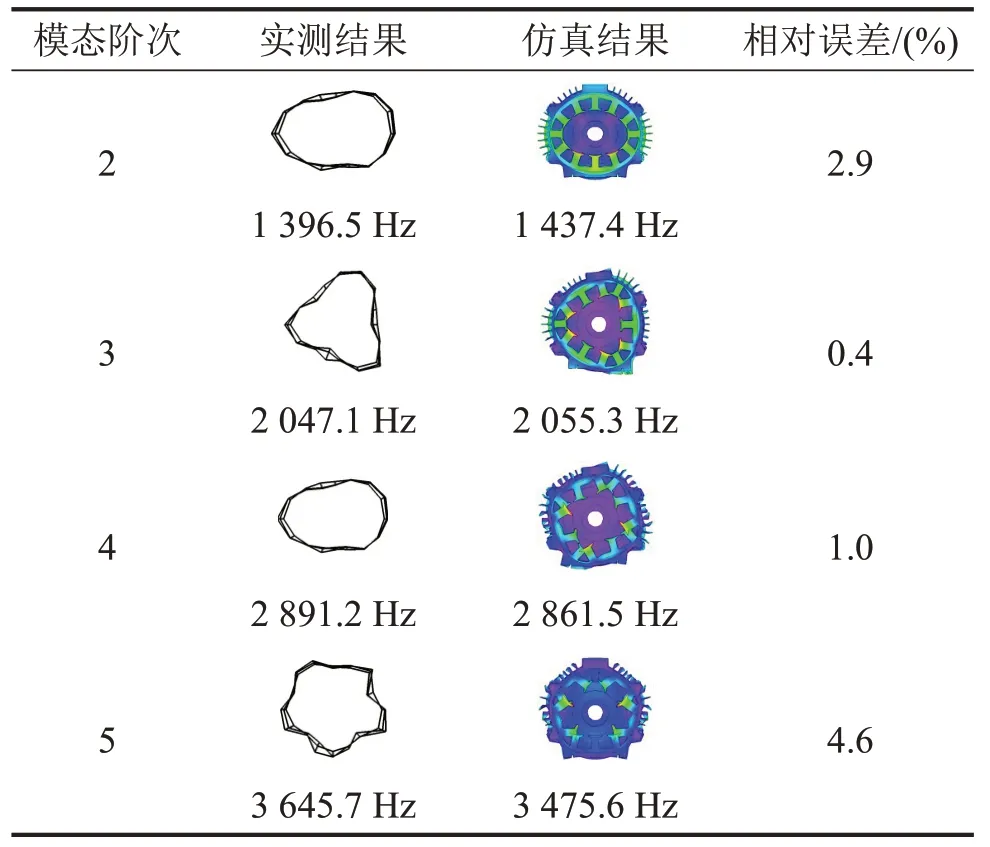
表5 模態參數實驗驗證

電機的結構特性對其振動噪聲影響較大，當電磁力頻率與固有頻率接近時會引起共振，進而惡化電機的振動噪聲[20]。本文主要分析高頻部分，即載波頻率附近的邊帶分量。結合圖7 可知，邊帶電磁力的頻率在8 000 Hz 附近，與結構的前5 階固有頻率相差較大，因此不易產生共振現象。

3.4 振動響應

為計算樣機的振動噪聲響應結果，建立了多物理場仿真模型，計算流程如圖8所示。首先，基于二維電磁模型得到作用在定子齒表面的節點力，并將節點力映射到結構模型中作為激勵，最后通過模態疊加法計算樣機的振動響應。

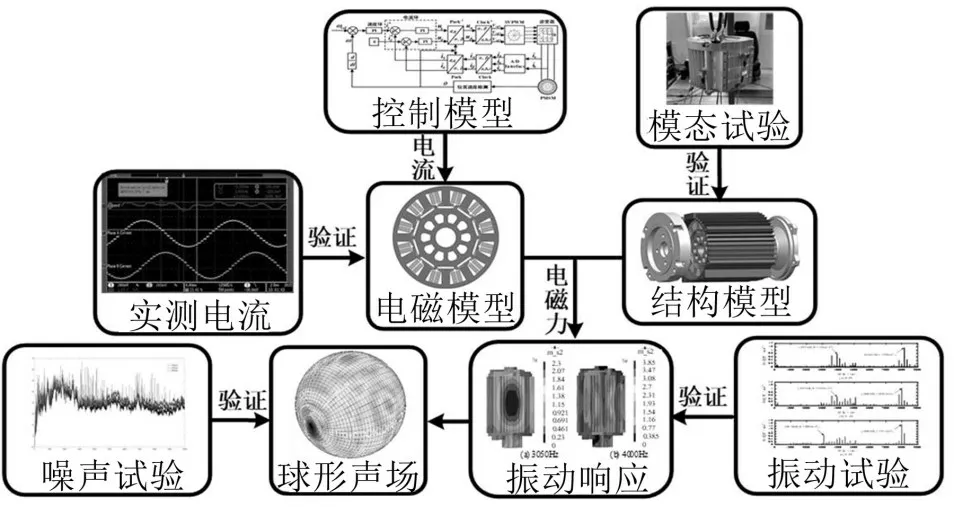
圖8 電機振動噪聲分析流程

模態疊加法的公式可表示為[21]：

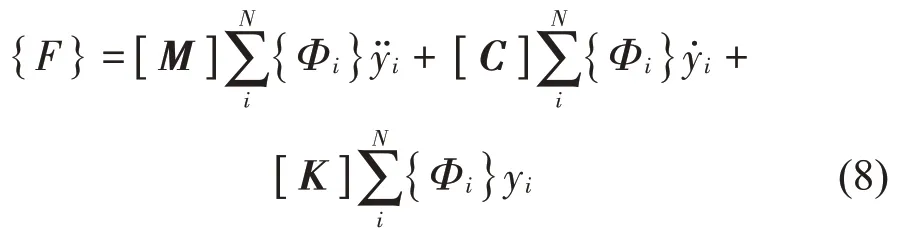
式中：[M]、[C]和[K]分別為質量、阻尼和剛度矩陣；N為疊加的模態階次；Фi為第i階模態振型；yi為節點模態坐標系中的位移。

為驗證計算結果的準確性，本文進行了實驗驗證，振動噪聲實驗臺架如圖9所示。

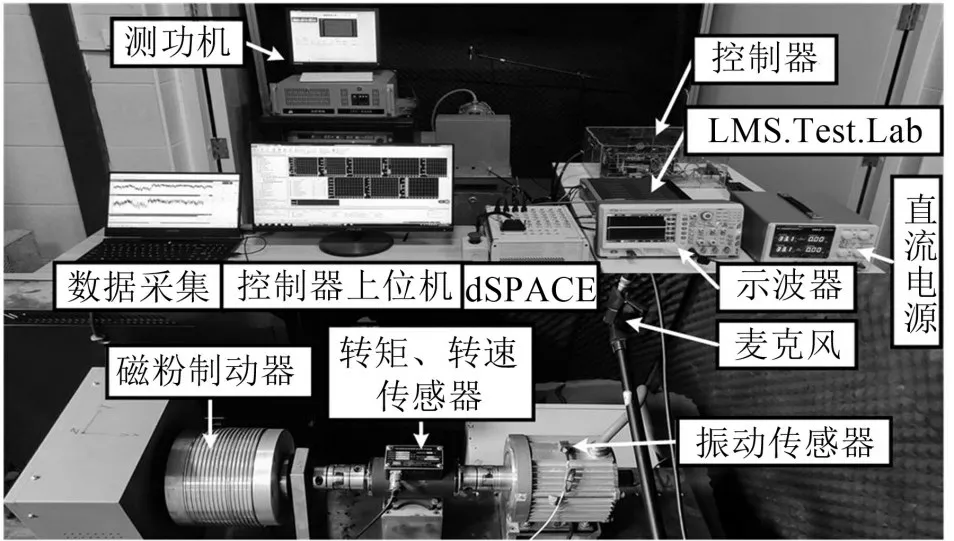
圖9 電機振動噪聲實驗臺

基于dSPACE 半實物仿真系統，利用Simulink和電機控制器來實現PWM 信號發波及調制策略的實時切換。圖10 為6 種DPWM 模式下樣機的振動加速度頻譜，可以看出,邊帶特征頻率較為明顯，仿真結果與實測數據基本吻合。DPWMMIN 與DPWMMAX 的振動峰值頻率為fc，由于該類型DPWM的邊帶電流諧波幅值較大，導致電機的振動特性有所惡化。對于DPWM0與DPWM2，其峰值頻率為fc±3f0，相比于DPWMMIN與DPWMMAX，該類型DPWM的振動特性有所改善。DPWM1與DPWM3的邊帶振動加速度峰值位于fc±6f0，相比于其他DPWM類型，其振動加速度幅值最低。結合邊帶電磁力頻譜可知，邊帶振動分量與邊帶電磁力的頻率特征基本一致，表明邊帶電磁力是產生電機高頻邊帶振動的主要原因。

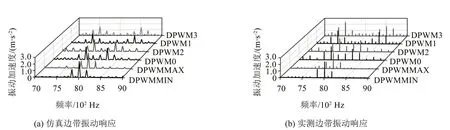
圖10 1 000 r/min和4 N·m工況下DPWM邊帶振動響應分析

4 電磁噪聲預測與驗證

基于前文振動響應分析結果，預測了6 種DPWM 策略下的樣機噪聲。為更好地反映人耳對實驗中所測噪聲的真實感受，采用A 計權dB(A)法對實驗所得聲學結果進行處理。圖11 所示為1 000 r/min和4 N?m工況下，樣機高頻邊帶噪聲A計權聲壓級的仿真結果與實測數據對比。可以看出，由邊帶電磁力所引起的高頻電磁噪聲具有明顯的頻率特征。DPWMMIN與DPWMMAX的邊帶噪聲峰值為59.2 dB，對應特征頻率為fc，其邊帶噪聲幅值是6 種DPWM 中最高的。相比于DPWMMIN 與DPWMMAX，DPWM0 與DPWM2 的噪聲特性有所改善，其邊帶噪聲峰值為57.5 dB，對應特征頻率為fc-3f0。DPWM1 與DPWM3 的邊帶噪聲幅值最低，其值為56.1 dB，對應特征頻率為fc-6f0。可以看出，這些邊帶噪聲分量都是由邊帶電流諧波所引起的，驗證了用于電磁噪聲計算的多物理場協同仿真模型的準確性。由于仿真計算只考慮電磁力對振動噪聲的影響，忽略了實驗臺架裝配誤差及控制器諧波豐富等非理想因素，進而導致部分頻率的仿真結果略低于實驗值。

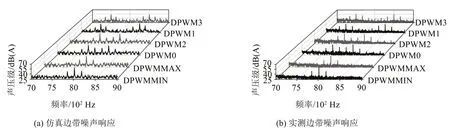
圖11 1 000 r/min和4 N·m工況下DPWM邊帶噪聲響應分析

5 結語

本文研究了基于DPWM 策略的永磁同步電機邊帶振動聲學特性，分析了邊帶電流諧波與徑向電磁力之間的關系；建立了“機-電-磁-控”協同仿真預測模型，對6 種DPWM 策略邊帶聲振響應的頻譜分布與幅值特征進行了數值預測。通過12槽-10極的永磁同步樣機穩態工況實驗，驗證了理論分析和協同仿真預測模型的準確性，得出結論如下：

（1）基于多物理場構建的協同仿真模型能夠準確預測各DPWM方案的邊帶聲振響應；通過模態試驗獲取了結構本身的固有特性并對有限元模型進行修正，實測與仿真振型及頻率誤差均在5%以內。

（2）6 種DPWM 策略中，DPWMMIN 與DPWMMAX策略的邊帶聲振響應幅值最高，峰值集中在中心頻率fc處；DPWM0與DPWM2策略的聲振響應幅值相對DPWMMIN 與DPWMMAX 較低，峰值位于fc±3f0；DPWM1 與DPWM3 策略的聲振響應幅值最低，峰值位于fc±6f0。

（3）本文所提出的分析方法可適用于多種PWM策略下永磁同步電機的邊帶聲振預測分析，可為永磁同步電機的邊帶聲振特征識別與優化提供新思路。