基于接觸有限元的斜齒輪副嚙合動態(tài)響應(yīng)及頻譜特性分析

陳彥齊，黃修長,2，華宏星,2

（1.上海交通大學(xué) 振動沖擊噪聲研究所，上海 200240；2.上海交通大學(xué) 機(jī)械系統(tǒng)與振動國家重點(diǎn)實(shí)驗室，上海 200240）

齒輪傳動裝置是機(jī)械傳動系統(tǒng)中的關(guān)鍵設(shè)備之一，被廣泛運(yùn)用于航空、船舶等領(lǐng)域。隨著實(shí)際運(yùn)用要求的提高，對齒輪的振動噪聲水平以及傳動系統(tǒng)的動態(tài)特性提出了更高的要求。齒輪嚙合過程中由于嚙合沖擊、轉(zhuǎn)速波動、時變嚙合剛度、輸入波動、基礎(chǔ)振動等因素具有強(qiáng)烈的非線性特征。發(fā)展準(zhǔn)確的齒輪系統(tǒng)的建模及計算方法，研究齒輪系統(tǒng)的動態(tài)特性及影響規(guī)律，對明確齒輪系統(tǒng)的振動機(jī)理及齒輪系統(tǒng)減振降噪具有重要意義。

針對齒輪系統(tǒng)的較為常用的建模方法是集中參數(shù)法。Tuplin[1]提出了采用質(zhì)量-彈簧模型模擬齒輪模型，以嚙合剛度等效齒輪間的嚙合作用，成為集中參數(shù)法建模的理論基礎(chǔ)。王峰[2]基于集中質(zhì)量法建立了人字齒輪的12自由度模型，模型中考慮了時變剛度、嚙合沖擊以及齒面摩擦等因素，研究結(jié)果表明，嚙合剛度激勵占振動的主要成分。集中參數(shù)法將軸與軸承的剛度直接等效為彈簧，未能考慮包含軸、軸承在內(nèi)的轉(zhuǎn)子系統(tǒng)的動力學(xué)特性。常樂浩[3]采用子結(jié)構(gòu)法推導(dǎo)了平行軸齒輪傳動系統(tǒng)通用建模方法，較之于前人工作添加了箱體單元，采用Newmark積分法與傅里葉級數(shù)法分別求解，驗證了該建模方法的有效性以及相較于集中質(zhì)量法建模的優(yōu)越性。Ouyang等[4]建立了考慮時變剛度與接觸非線性特性的齒輪-滾子-軸承系統(tǒng)動力學(xué)模型，結(jié)果表明齒輪傳動系統(tǒng)產(chǎn)生的動態(tài)激勵是高速條件下的主要振動源。

隨著有限元商業(yè)軟件的發(fā)展，逐步采用有限元軟件如ABAQUS、ANSYS 等建立了完整的齒輪傳動系統(tǒng)有限元模型，具有更高的準(zhǔn)確度，在建模過程中不需人為考慮非線性因素，求解更為簡便，并且能得到齒輪副在嚙合過程中的動態(tài)接觸力等實(shí)驗難以測得的量。Chen等[5]通過有限元方法研究了行星齒輪外圈厚度對嚙合剛度的影響，并與集中參數(shù)法結(jié)合求解得到齒輪系統(tǒng)的動態(tài)響應(yīng)，發(fā)現(xiàn)會出現(xiàn)調(diào)制現(xiàn)象，但未對調(diào)制現(xiàn)象做出詳細(xì)解釋。Stoyanov等[6]通過ABAQUS建立了行星齒輪的有限元模型，并計算得到各齒輪中心的響應(yīng)，表明接觸有限元方法對了解系統(tǒng)動態(tài)特性的有效性。吳勇軍等[7－8]基于ANSYS軟件建立了齒輪-軸-軸承耦合系統(tǒng)的動力學(xué)模型，求解得到了系統(tǒng)的動力學(xué)特性，結(jié)果表明轉(zhuǎn)子系統(tǒng)響應(yīng)中不僅包含嚙合頻率及其倍頻，還包含齒輪系統(tǒng)平均等效頻率、彎曲振動固有頻率等成分。張濤等[9]在齒輪副的基礎(chǔ)上，引入軸與軸承，采用ABAQUS軟件對人字齒輪進(jìn)行動力學(xué)仿真，研究了系統(tǒng)阻尼、輸入轉(zhuǎn)速等因素對齒輪沖擊嚙合特性的影響。Ericson等[10]通過接觸有限元對行星齒輪彈性體進(jìn)行仿真，仿真結(jié)果與實(shí)驗結(jié)果較為吻合，結(jié)果表明采用有限元方法能夠獲得集中參數(shù)法沒有的模態(tài)，且彈性體振動與嚙合力激勵高度耦合。曹茂鵬等[11]采用有限元方法對直齒面齒輪動態(tài)嚙合力進(jìn)行仿真，得到了動態(tài)嚙合力的時域變化結(jié)果，研究了轉(zhuǎn)速等因素對嚙合力的影響。上述研究大都集中于驗證有限元軟件方法的計算正確性，在時域方面開展齒輪系統(tǒng)的動態(tài)響應(yīng)規(guī)律分析，在頻域方面未對齒輪系統(tǒng)的頻域特征做出詳細(xì)分析，通常頻率分辨率較低、頻譜特征不夠豐富、頻譜圖中僅有嚙合頻率及其倍頻的峰值、邊頻帶等特征被忽略的研究，不能詳細(xì)分析齒輪系統(tǒng)的振動機(jī)理。

基于ABAQUS商業(yè)有限元軟件，采用三維接觸有限元，建立了考慮軸及軸承剛度的一對斜齒輪副-軸-軸承系統(tǒng)動態(tài)嚙合有限元模型，發(fā)展對齒輪系統(tǒng)的一般性有限元分析方法。從多種工況下分析齒輪系統(tǒng)的動態(tài)響應(yīng)，驗證該方法的有效性，并且相較于現(xiàn)有研究結(jié)果，得到較高頻率分辨率、較為豐富的頻域特征。

1 有限元模型建立

對斜齒輪副采用Solidworks軟件進(jìn)行三維模型建模，斜齒輪副參數(shù)如表1 所示。然后進(jìn)行有限元網(wǎng)格劃分，為得到高質(zhì)量純六面體網(wǎng)格，將斜齒輪三維模型導(dǎo)入Hypermesh 進(jìn)行網(wǎng)格劃分。

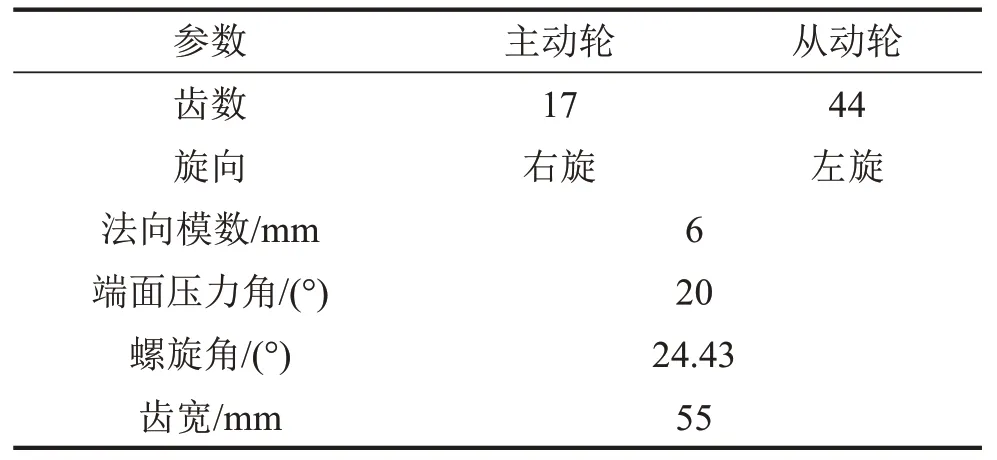
表1 齒輪副參數(shù)

將上述網(wǎng)格模型導(dǎo)入到ABAQUS，進(jìn)行有限元仿真設(shè)置和計算。軸-軸承參數(shù)及運(yùn)行仿真參數(shù)如表2所示。采用647 992個C3D8單元對齒輪進(jìn)行建模、采28個B31梁單元對軸進(jìn)行模擬、采用4個賦予剛度屬性的Wire 單元對軸承進(jìn)行模擬。采用Dynamic/Implicit求解器進(jìn)行求解，設(shè)置分析時間總長為1 s，時間增量步長設(shè)為自動調(diào)整，最小增量步長設(shè)置為1×10-8。將主動輪與從動輪設(shè)為接觸對，采用面-面接觸類型，齒輪接觸選用有限滑動接觸，并設(shè)置其接觸屬性的法向行為為硬接觸，在此不考慮齒面間的摩擦作用，因此切向設(shè)置為無摩擦。

表2 軸-軸承參數(shù)及運(yùn)行仿真參數(shù)

在齒輪內(nèi)孔面與軸的中點(diǎn)建立運(yùn)動耦合約束，以對主動輪及從動輪的邊界條件及載荷進(jìn)行控制；在從動輪中心添加扭矩，在主動輪中心添加轉(zhuǎn)速，以模擬齒輪系統(tǒng)運(yùn)轉(zhuǎn)工況。為保證計算模型分析收斂，共設(shè)置2 個分析步，第一個分析步固定從動輪，主動輪轉(zhuǎn)動0.05 rad，保證兩個齒輪充分接觸；第二個分析步釋放從動輪的自由度，如前所述添加主動輪角速度與從動輪扭矩。

根據(jù)釋放從動輪自由度的個數(shù)，共劃分3 種工況：

(1)從動輪軸與從動輪內(nèi)孔面耦合的節(jié)點(diǎn)只釋放繞軸旋轉(zhuǎn)自由度；

(2)對從動輪軸與從動輪內(nèi)孔面耦合的節(jié)點(diǎn)不作約束，此時靠軸端的彈簧單元約束系統(tǒng)的自由度；

(3)對從動輪軸與從動輪內(nèi)孔面耦合的節(jié)點(diǎn)不作約束，并且在此節(jié)點(diǎn)上添加大小為1 000 N的軸向靜推力。其中第一種工況齒輪旋轉(zhuǎn)中心只有旋轉(zhuǎn)自由度，是較為理想的工況，模擬軸、箱體、基座的剛度都較大的情況；第二種工況是一般性工況，考慮軸、軸承的剛度；第三種工況是研究軸向靜推力負(fù)載下齒輪系統(tǒng)動力學(xué)特性。系統(tǒng)有限元模型如圖1所示。

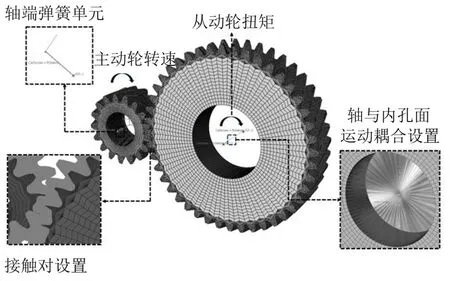
圖1 斜齒輪副-軸-軸承系統(tǒng)有限元模型

2 動態(tài)響應(yīng)結(jié)果及分析

計算完成后，導(dǎo)出大齒輪中心的角速度、角加速度和齒輪副的動態(tài)接觸力。齒輪副在嚙合點(diǎn)處的加速度可作為評估齒輪系統(tǒng)的動態(tài)性能指標(biāo)之一[10]，其定義為：

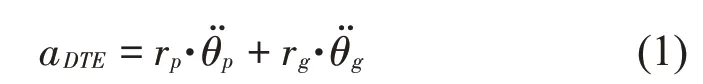
式中：rp、分別為主動輪的基圓半徑與角加速度；rg、分別為從動輪的基圓半徑與角加速度。仿真中，主動輪的角加速度為0，因此根據(jù)從動輪加速度即可評估系統(tǒng)的動態(tài)性能。

主動輪轉(zhuǎn)頻為20.0 Hz，從動輪轉(zhuǎn)頻為7.7 Hz，系統(tǒng)的嚙合頻率為340 Hz，理論角速度為48.550 5 rad/s，理想平穩(wěn)狀態(tài)下齒輪的法向接觸力可用式(2)進(jìn)行計算：

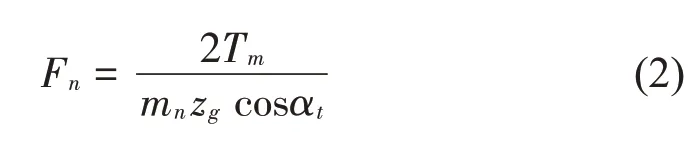
式中：Tm為負(fù)載扭矩，mn為法向模數(shù)；zg為從動輪齒數(shù)；αt為端面壓力角。將仿真模型參數(shù)代入公式進(jìn)行計算，得到理論法向接觸力為2 419 N。

2.1 從動輪中心僅釋放旋轉(zhuǎn)自由度工況

從動輪中心僅釋放旋轉(zhuǎn)自由度工況下從動輪的角速度、角加速度及齒輪副動態(tài)接觸力時域結(jié)果如圖2所示。由圖2可知，由于時變嚙合剛度等非線性因素存在，時域結(jié)果存在明顯周期性波動與峰值，角速度的均值與均方根值都為48.550 8 rad/s。峰值的間隔周期約為0.05 s，與主動輪的轉(zhuǎn)動周期較為接近，伴隨明顯的沖擊現(xiàn)象。角加速度的均方根值為70.692 0 rad/s2，動態(tài)接觸力的均方根值為2 453.6 N。相較平穩(wěn)狀態(tài)理論值增加1.4%，表明在從動輪中心僅釋放旋轉(zhuǎn)自由度工況下，齒輪系統(tǒng)的非線性因素對于齒輪動態(tài)接觸力的影響不大。

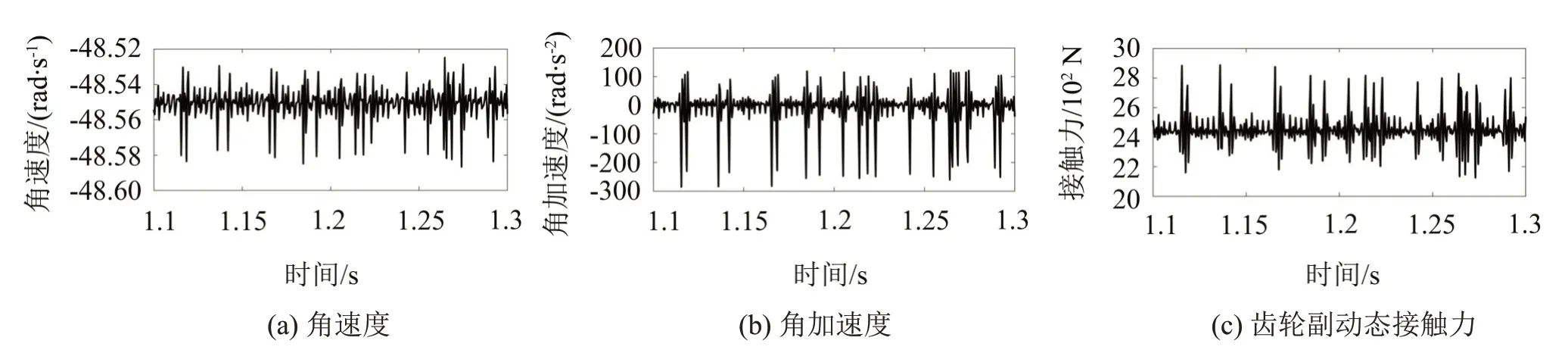
圖2 從動輪中心僅釋放旋轉(zhuǎn)自由度工況下從動輪時域結(jié)果

對信號進(jìn)行去均值處理之后采用傅里葉變換將時域結(jié)果變換至頻域，頻率分辨率為1 Hz，得到角速度、角加速度、動態(tài)接觸力的脈動量頻譜結(jié)果如圖3所示。可見，主要成分為主動輪轉(zhuǎn)頻20 Hz 及其倍頻；頻譜的突出峰值為340 Hz、680 Hz、640 Hz、720 Hz 等頻率，其中340 Hz 是該齒輪系統(tǒng)的嚙合頻率，680 Hz 為嚙合頻率二倍頻，其余頻率皆為主動輪轉(zhuǎn)動頻率的多倍頻。在從動輪中心僅釋放旋轉(zhuǎn)自由度工況下，響應(yīng)頻率主要由主動輪轉(zhuǎn)頻及其多倍頻與嚙合頻率及其倍頻組成。

2.2 從動輪中心不作約束工況

從動輪中心不作約束工況下的角速度、角加速度、齒輪副法向接觸力時域結(jié)果如圖4所示。

將圖4 與圖2 比較，當(dāng)齒輪中心浮動，引入軸的剛度與軸承的剛度，角速度、角加速度及動態(tài)接觸力沒有呈現(xiàn)明顯的沖擊現(xiàn)象，依舊保持明顯的周期特性伴隨著波動幅值增加。在此工況下，角速度的均方根值為48.556 3 rad/s，與理論角速度相差0.005 8 rad/s，但中心固定時的角速度均方根值僅為0.000 3 rad/s。角加速度的均方根值增至143.695 4 rad/s2，反映系統(tǒng)的振動加劇。動態(tài)接觸力均方根值增至2 677.5 N，動態(tài)接觸力相較于靜態(tài)接觸力或中心固定工況下的接觸力增加了約258 N，增加了10%。3個物理量均能反映在引入軸剛度與軸承剛度之后，齒輪系統(tǒng)的振動加劇。

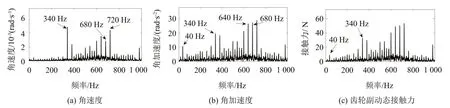
圖3 從動輪中心只釋放旋轉(zhuǎn)自由度工況下從動輪頻域結(jié)果

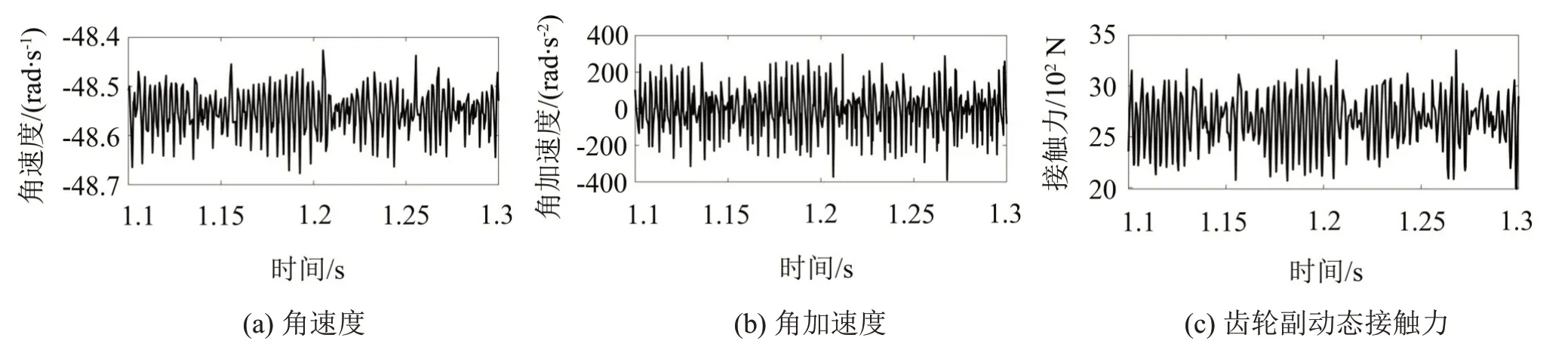
圖4 從動輪中心不作約束工況下從動輪響應(yīng)時域結(jié)果

將時域結(jié)果進(jìn)行傅里葉變換，頻域結(jié)果如圖5所示。為與中心只有旋轉(zhuǎn)自由度的工況進(jìn)行對比，將幅值范圍與圖3 統(tǒng)一，其中嚙合頻率附近的幅值較大，此部分的頻譜圖如框線中的頻譜所示。由圖5(a)可知，300 Hz 以內(nèi)存在主動輪轉(zhuǎn)頻20 Hz 及其多倍頻。與圖3(a)相比，400 Hz 及以上的頻率成分減少，嚙合頻率及其附近的幅值顯著增大。圖3(a)中嚙合頻率處的幅值大小為0.005，圖5(a)中嚙合頻率處的幅值增至0.03。此現(xiàn)象也同樣存在于角加速度與動態(tài)接觸力的頻譜中，較高頻段處的幅值減小，嚙合頻率及其附近頻段的幅值顯著增大。

除此之外，對比圖3 與圖5 可知，考慮系統(tǒng)的軸剛度及軸承剛度時，在嚙合頻率處的幅值大幅增加同時，會出現(xiàn)以從動輪轉(zhuǎn)頻為調(diào)制頻率的邊頻帶。如圖5(a)中的332 Hz是由嚙合頻率340 Hz減去從動輪轉(zhuǎn)頻所得，其幅值為0.01；353 Hz是由嚙合頻率加上從動輪二倍轉(zhuǎn)頻，其幅值為0.008；此現(xiàn)象同樣也存在于角加速度與法向接觸力的頻譜中。

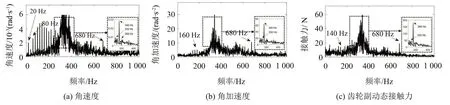
圖5 從動輪中心不作約束工況下從動輪響應(yīng)頻域結(jié)果

丁康等[12]發(fā)現(xiàn)齒輪嚙合過程中，會出現(xiàn)以嚙合頻率及其倍頻為載波頻率、齒輪的轉(zhuǎn)動頻率為調(diào)制頻率的調(diào)制現(xiàn)象并對其進(jìn)行定性分析。可從幅值調(diào)制與頻率調(diào)制兩方面進(jìn)行分析。從幅值調(diào)制的角度認(rèn)為齒輪系統(tǒng)的動態(tài)響應(yīng)如式(3)所示：

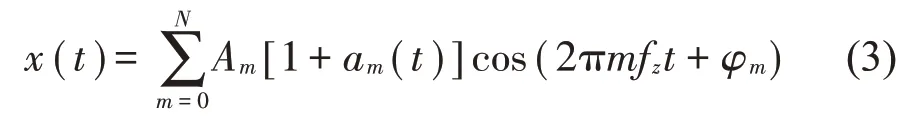
其中：Am是第m階幅值，fz是嚙合頻率，[1+am(t)]是與齒輪轉(zhuǎn)動頻率有關(guān)的調(diào)制信號，可以被表示為am(t)=βmcos(2πmfnt)，其中fn為從動輪的轉(zhuǎn)頻。利用積化和差公式將式(3)的第m階展開可得：

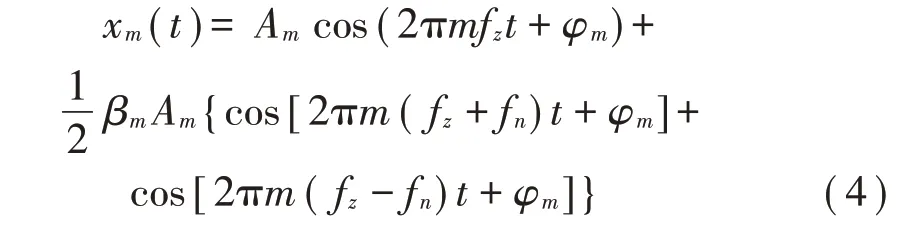
式(4)表明，除了嚙合頻率成分外，還會出現(xiàn)頻率為fz+fn與fz-fn的成分。

楊小青[13]提出齒輪動態(tài)響應(yīng)的調(diào)頻現(xiàn)象可從齒輪的轉(zhuǎn)速波動對嚙合頻率的影響進(jìn)行分析，將齒輪副的嚙合剛度以嚙合頻率為基頻進(jìn)行傅里葉展開：

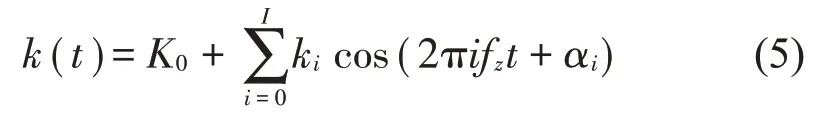
其中：K0為平均嚙合剛度，fz為嚙合頻率，ki和αi為第i階分量的幅值與相位。較為普遍的集中參數(shù)模型建模方法中假設(shè)嚙合頻率是一個在穩(wěn)定轉(zhuǎn)速下計算出來的恒定值，但是由于齒輪實(shí)際上為彈性體，齒輪在轉(zhuǎn)動過程中包含摩擦、沖擊等非線性因素，如圖2、圖4 所示，從動輪轉(zhuǎn)速會存在波動。將轉(zhuǎn)速的波動成分以傅里葉級數(shù)形式表示，波動轉(zhuǎn)速表示如下：

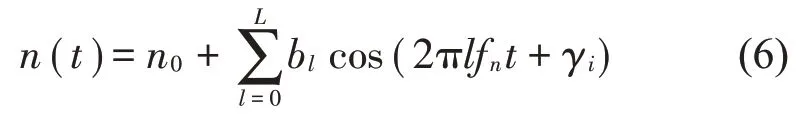
其中：n0為理論轉(zhuǎn)速，fn為從動輪轉(zhuǎn)頻，考慮轉(zhuǎn)速波動時嚙合頻率計算公式為：

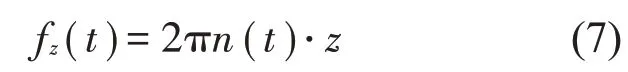
將式(6)與式(7)代入式(5)，可得到考慮波動轉(zhuǎn)速的嚙合頻率表達(dá)式：

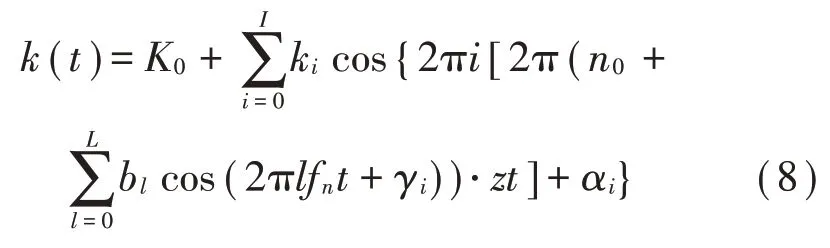
將式(8)的第i階分量的相位記為Φi(t)，則Φi(t)表達(dá)如式(9)所示，對其相位進(jìn)行求導(dǎo)，如式(10)所示，即可得到頻率表達(dá)式：

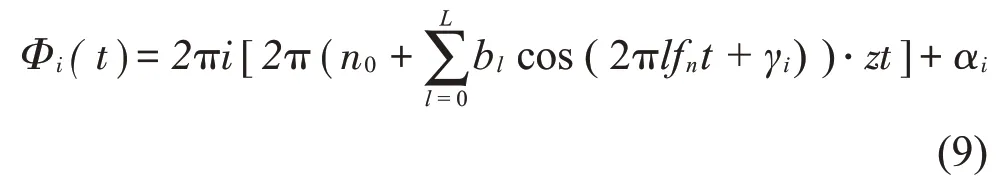
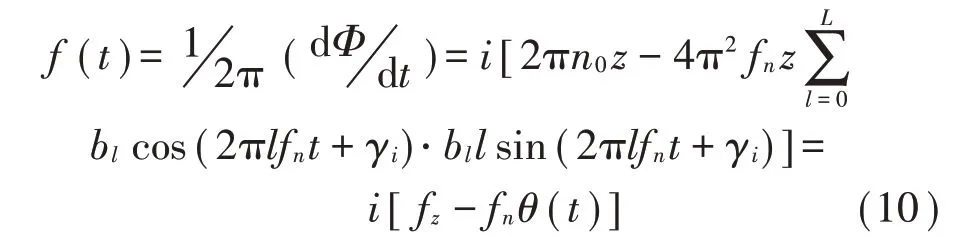
由式(10)發(fā)現(xiàn)考慮轉(zhuǎn)速波動時，除理論的嚙合頻率以外，嚙合剛度會出現(xiàn)與轉(zhuǎn)頻相關(guān)的頻率成分。通過對調(diào)制現(xiàn)象進(jìn)行定性分析，說明了仿真結(jié)果中出現(xiàn)調(diào)制現(xiàn)象的合理性，同時也證明采用有限元方法能夠得到更詳細(xì)的頻率特征。

2.3 從動輪中心不作約束且添加軸向靜推力工況

從動輪中心浮動且在從動輪中心添加軸向1 000 N 靜推力工況下的角速度、角加速度、齒輪副法向接觸力時域結(jié)果如圖6所示。添加軸向靜推力之后的時域響應(yīng)相較于沒有添加軸向靜推力的結(jié)果沒有明顯差異，呈現(xiàn)周期性波動特征。其角速度均方根值為48.557 4 rad/s，與理論角速度相差0.006 9 rad/s；其角加速度均方根值為153.968 5 rad/s2，相較于不添加軸向靜推力的工況增加10.273 1 rad/s2；動態(tài)接觸力均方根值增至2 680.8 N，相較于不添加軸向靜推力工況增加約3 N，可以忽略不計。

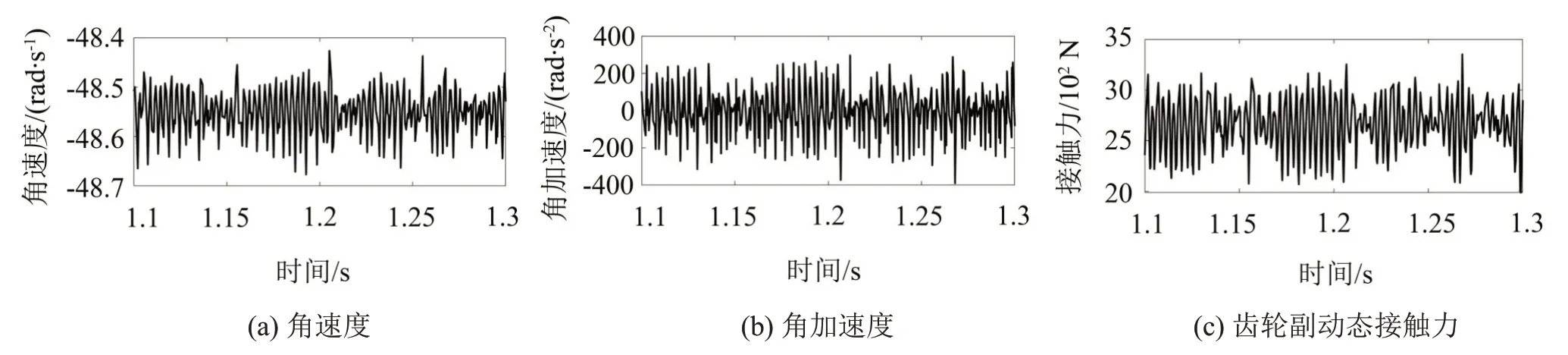
圖6 從動輪中心不作約束且添加軸向靜推力工況下從動輪響應(yīng)時域結(jié)果

3種工況下各指標(biāo)的時域結(jié)果比較如表3所示，從表中可以看出，引入軸及軸承的剛度之后，系統(tǒng)的振動加劇，各指標(biāo)的均方根值都有所增加，其中角加速度與動態(tài)接觸力的增加較為明顯；添加1 000 N軸向靜推力對系統(tǒng)的動態(tài)響應(yīng)特性影響較小。

表3 3種工況下各指標(biāo)均值、均方值比較

將時域結(jié)果通過傅里葉變換至頻域，如圖7 所示。從圖7 可知，添加軸向力的頻譜圖與未添加軸向力的頻譜圖較為接近。與未添加軸向力的頻譜相比較，3個指標(biāo)的頻率特征沒有明顯變化，保持以嚙合頻率為主，嚙合頻率附近出現(xiàn)以從動輪轉(zhuǎn)頻及其倍頻為調(diào)制頻率的調(diào)制現(xiàn)象。

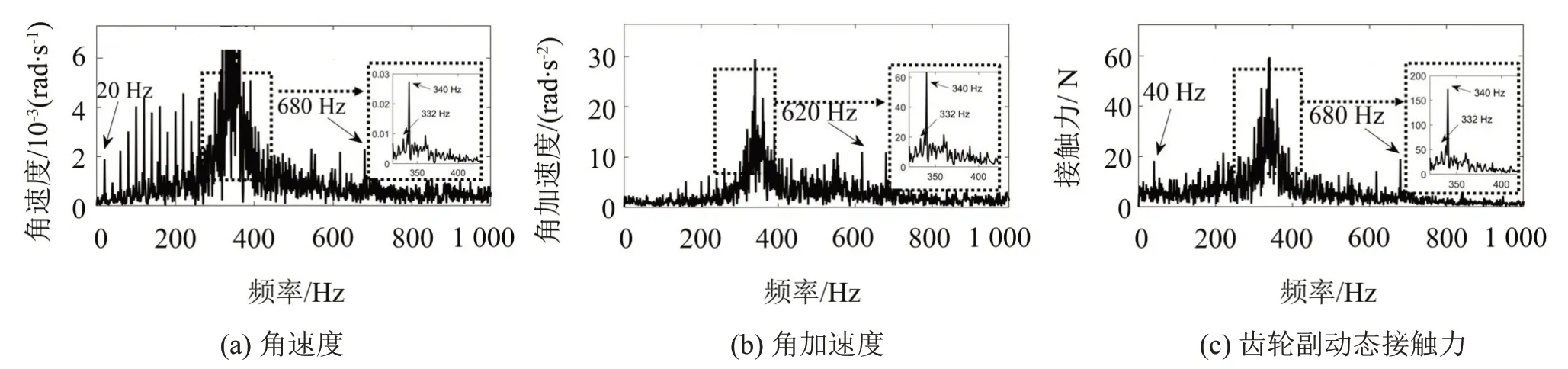
圖7 從動輪中心不作約束且添加軸向靜推力工況下從動輪響應(yīng)頻域結(jié)果

時域結(jié)果以及頻域結(jié)果都能表明，在從動輪中心添加大小為1 000 N 的靜推力對于齒輪系統(tǒng)的動態(tài)響應(yīng)影響很小。

3 結(jié)語

基于接觸有限元方法，建立了齒輪副-軸-軸承耦合系統(tǒng)，發(fā)展了更精確地分析齒輪系統(tǒng)動態(tài)響應(yīng)及特性的方法，研究了從動輪中心僅釋放旋轉(zhuǎn)自由度、從動輪中心不作約束、從動輪中心不作約束且添加軸向靜推力3 種工況下的動態(tài)響應(yīng)，得出了以下結(jié)論：

(1)從動輪中心僅釋放旋轉(zhuǎn)自由度工況下的系統(tǒng)角速度、角加速度、動態(tài)接觸力的波動要小于其余兩種工況，反映了在考慮軸、軸承的剛度之后系統(tǒng)的振動加劇，且存在較為明顯的周期性沖擊現(xiàn)象；添加1 000 N 軸向靜推力與未添加軸向靜推力相比對系統(tǒng)的動態(tài)響應(yīng)影響不大；

(2)從動輪中心僅釋放旋轉(zhuǎn)自由度工況下的頻譜特征以主動輪轉(zhuǎn)頻及其倍頻為主；對從動輪中心不作約束時，頻譜特征呈現(xiàn)以嚙合頻率載波頻率，以從動輪轉(zhuǎn)頻及其倍頻為調(diào)制頻率的調(diào)制現(xiàn)象，并從幅值調(diào)制和頻率調(diào)制兩方面定性分析了頻譜出現(xiàn)邊頻帶的原因。