板式擴散焊矩形微通道換熱器中S-CO2 流動與傳熱特性的數值模擬

李 洪， 任 燕， 章立新， 高 明， 劉婧楠， 楊其國

(1.上海理工大學 能源與動力工程學院，上海 200093； 2.上海市動力工程多相流動與傳熱重點實驗室，上海 200093)

發展新型高效發電技術是提高能源利用效率、實現節能環保最直接有效的方式[1]。相對于傳統工質的動力循環系統，超臨界二氧化碳(S-CO2)布雷頓循環系統具有效率高、潔凈度高、靈敏度高、成本低以及結構緊湊等優點[2]，被認為是新興能源利用方式中最具應用前景的能源轉換系統之一，得到了國際學術界和工業界的廣泛關注[3]。

目前，S-CO2布雷頓循環已成為第四代先進核能系統的備選熱力方案之一[4]。循環系統中的熱交換器(如預冷器、回熱器等)是系統中的重要部件，直接影響著整個系統的高效性和緊湊性。印刷電路板式換熱器(PCHE)自面世以來，由于性能優勢，且契合我國能源技術轉型升級和未來碳中和的需求[5]，在太陽能工程、液化天然氣工程和核反應堆工程等領域得到了廣泛的關注[6]。研究表明，使用條件、流體流態及通道結構等因素均會影響PCHE的流動與傳熱特性，且在確定的應用背景下，通道結構的影響最為顯著。PCHE通道結構分為連續型和非連續型，涵蓋直線型、折線型、S形和翼型等多種形式；通道截面包括圓形、半圓形、矩形、三角形和梯形等多種形狀。受制于蝕刻加工技術，目前半圓形截面通道的研究應用較為廣泛[7]。Geyer等[8]在恒定熱流密度的邊界條件下，對比分析了半圓形截面直線型通道與S形通道的傳熱效果，結果表明對于充分發展的層流流動而言，S形通道能夠達到強化傳熱的目的，同等工況下的強化效果可達2.5～3倍。Gupta等[9]探索了恒定熱流密度時通道截面形狀對傳熱特性的影響，結果表明在雷諾數(Re)低于200時，不同截面形狀的傳熱效果為三角形>矩形>半圓形>圓形。Lee等[10]對比了折線型通道不同截面形狀對傳熱特性和壓降特性的影響，證實矩形通道同時具有最佳的傳熱特性和最大的阻力損失。范凌灝等[11]的研究發現，在保持矩形微通道當量直徑不變的情況下，隨著截面高寬比的增大，通道表面的平均努塞爾數逐漸升高，傳熱性能得到提升，但壓降也隨之增大，流動惡化，微通道換熱器的綜合性能降低。Cui等[12]對翼型翅片通道的分析結果表明，將形狀適宜的翅片交錯排布可以使得近壁邊界層周期性發展和消失，削弱邊界層對流動傳熱的影響，實現強化傳熱。綜上可知，優化通道的截面形狀及擾流部件有助于實現強化傳熱、改善流動特性，但往往會造成生產工藝復雜、生產成本高昂等問題。因此，加工工藝便捷高效的矩形通道型PCHE在實現其流動與傳熱綜合性能優化之后，將會擁有廣闊的應用前景。

此外，S-CO2布雷頓循環系統中PCHE內的工質為超臨界流體，超臨界流體是當CO2的溫度和壓力均高于臨界點(31 ℃和7.4 MPa)之后的一種狀態，其基本物理性質(包括密度、黏度及擴散性等)均處于氣體與液體之間，具有氣液的雙重特性：其黏度和擴散系數接近氣體，因此具有良好的流動性能、滲透性能和傳遞性能[13]。

隨著對PCHE研究的不斷深入，以S-CO2為循環工質的實驗和理論研究在流動范圍、應用領域等方面仍然存在以下不足之處：通道內S-CO2流動與傳熱局限于低雷諾數范圍，且冷側和熱側通道內工質均為S-CO2的研究尚不充分等[14]。為此，筆者以S-CO2為循環工質，對板式擴散焊矩形微通道換熱器內的流動與傳熱特性展開數值模擬，建立了適用的流動與傳熱數學物理模型，探索不同Re條件下擾流格柵對微通道內流動與傳熱特性的影響機理，從微通道的流動特性、傳熱特性及綜合性能等角度進行分析，以提高微通道換熱器的流動換熱綜合性能，并為換熱器的結構優化提供理論依據。

1 板式擴散焊矩形微通道換熱器的數學物理模型

1.1 物理模型及邊界條件

傳統PCHE的加工是通過在金屬板片上進行光電化學刻蝕形成通道，其工藝復雜、成本高昂[15]。筆者選用的新型板式擴散焊矩形微通道換熱器結構如圖1所示。該換熱器利用激光切割316L不銹鋼金屬板片，隨后以擴散焊方式將9片金屬板按照一定次序堆疊形成一組冷熱通道，其中第1、第5、第9片為冷熱流體換熱界面，第2、第3、第4和第6、第7、第8片分別形成熱流體通道和冷流體通道(以下分別簡稱為熱通道和冷通道)，每3片金屬板的厚度為矩形微通道的高度，而冷熱通道中格柵分別位于第3和第7片，堆疊而成的逆流換熱單元如圖1(b)所示，經換熱單元周期性重復排列，最終組成一個完整的換熱器。

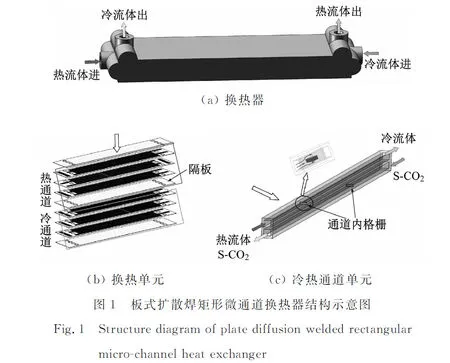
換熱器包含18個換熱單元，換熱器外觀尺寸長×寬×高為411.0 mm×112.0 mm×43.6 mm，其中矩形通道斷面尺寸為3.00 mm×2.85 mm，格柵高度為0.95 mm。格柵高度是本文換熱器結構中的最小幾何尺寸(即板片的厚度)，本文數值模擬所使用的網格在壁面附近需設置細密的邊界層，因此不宜直接選用完整的換熱器或者換熱單元作為數值模擬對象，以免影響數值模擬的效率和精度。為此，對換熱單元的結構進行了簡化，建立了如圖1(c)所示的冷熱通道單元的幾何模型，其中矩形通道與格柵等的幾何尺寸均為換熱器的實際尺寸。

此外，建立了總長度和當量直徑相同的半圓形直通道與矩形通道幾何模型，如圖2(a)所示，其中g為重力加速度。研究表明，在通道內增設擾流格柵，可以起到強化傳熱的效果[16]。因此，在圖2(c)所示的矩形通道基礎上，設置了如圖2(d)～圖2(g)所示的不同的擾流格柵，探索其對換熱單元流動與傳熱特性的影響。圖2(e)中的冷熱通道幾何模型即為圖1(c)所示的冷熱通道中部設置水平格柵的換熱器幾何模型。各個模型的相關幾何尺寸見表1。

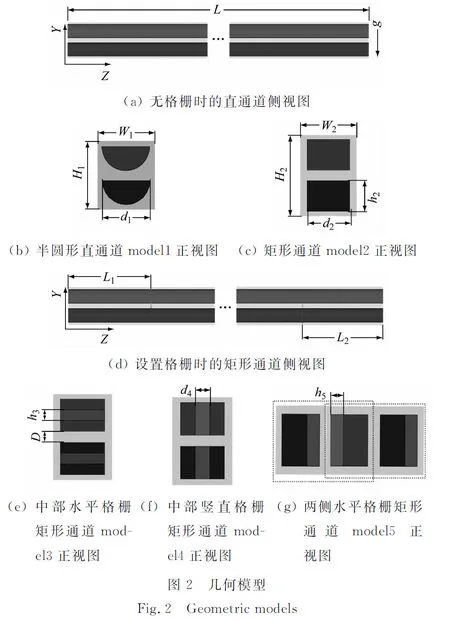
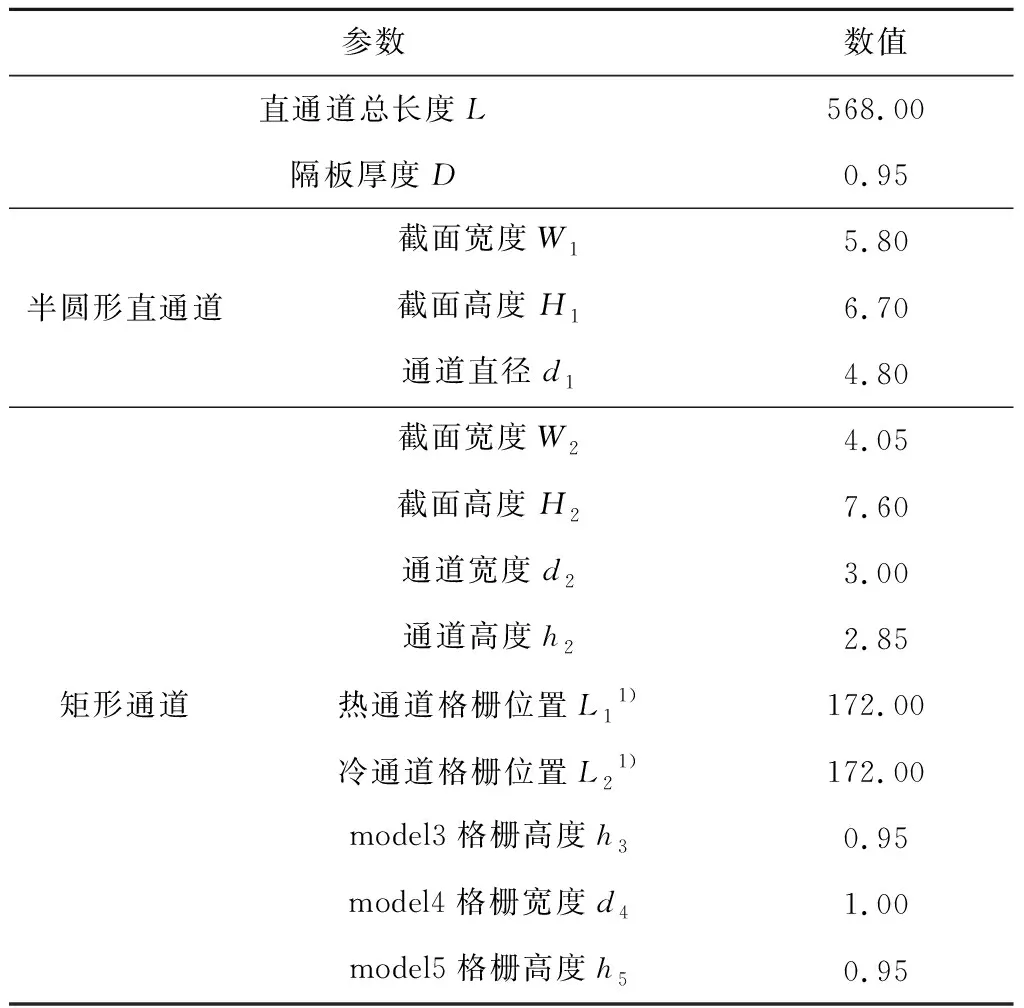
表1 冷熱通道結構參數

利用Ansys Fluent 18.0軟件展開數值模擬研究，其中S-CO2熱物性參數來自于REFPROP V9.1，并通過引入實際氣體模型(NIST Real Gas)實現動態求解。數值模擬邊界條件見表2，其中計算域固體區域材料為316L不銹鋼，其密度、比定壓熱容和導熱系數分別為8 360 kg/m3、0.417 kJ/(kg·K)和0.021 kW/(m·K)。

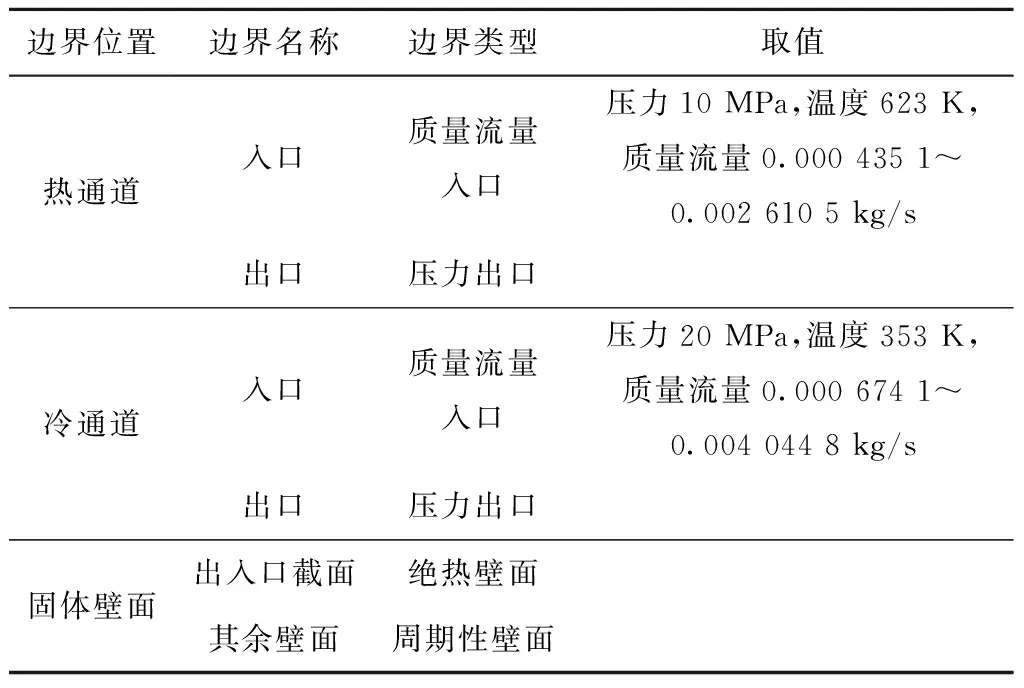
表2 數值模擬邊界條件

1.2 流動與傳熱模型

板式擴散焊矩形微通道中S-CO2流動與傳熱特性研究的數值模擬控制方程[17]如下：

連續性方程

div(ρu)=0

(1)

動量方程

(2)

ρg+Sv

(3)

(4)

能量方程

(5)

式中：ρ和μ分別為流體的密度和動力黏度；p和T分別為壓力和溫度；K和c分別為流體傳熱系數和比熱容；u、v和w分別為流體沿x、y和z方向的流速分量；S為廣義源項；μt為湍動黏度，本文選用SSTk-ω湍流模型進行湍流計算，因此μt根據式(6)[18]計算。

μt=ρk/ω

(6)

式中：k和ω分別為湍動能和湍動頻率，計算方法詳見式(7)和式(8)。

Yk+Sk

(7)

Yω+Sω

(8)

式中：Gk為由層流流速梯度而產生的湍動能；Gω為由ω方程產生的湍動能；Γk和Γω分別為k和ω的有效擴散率；Yk和Yω分別為k和ω的發散項；Sk和Sω為自定義源項。

數值模擬選用穩態計算，求解方法采用基于壓力-流速耦合的SIMPLE算法，壓力項采用二階迎風離散格式，梯度項采用格林-高斯離散格式，動量和能量均采用二階迎風離散格式。

1.3 流動與傳熱特性評價指標

選取努塞爾數(Nu)和流動摩擦阻力系數(f)表征S-CO2在不同通道內的傳熱特性和流動阻力特性。Nu越大表明流體與壁面之間的傳熱系數越大；f越大表明流體在通道內的流動損失越大[19]。Nu和f的計算方法如下：

(9)

(10)

式中：qw為監測得到的冷熱通道壁面熱通量；De為通道的當量直徑；λ為通道內流體的導熱系數；Tf和Tw分別為流體和壁面的溫度；Δp為通道進出口處流體之間的壓差；uc為流體流速。

為了兼顧傳熱特性和流動特性，以綜合傳熱增強因子(PEC)θ作為表征流動與傳熱特性的綜合指標，計算方法見式(11)。當PEC大于1時，表示綜合性能優于比較基準(以圖2(c)所示的無格柵矩形通道為比較基準，其努塞爾數和流動摩擦阻力系數分別為Nu0和f0)。

(11)

2 模型驗證

2.1 網格無關性驗證

通過Ansys ICEM在幾何模型計算域生成六面體結構化網格，網格質量在0.9以上。為準確反映通道內流體真實的流動與傳熱狀態，在冷熱通道壁面處設置了細密的邊界層網格。邊界層網格的初始高度為0.001 6 mm，增長率為1.2，以確保靠近壁面第一層網格節點處的y+小于1。

為驗證網格無關性，選取65萬、91萬、126萬和214萬4種網格數展開數值模擬。其中，冷、熱通道S-CO2的入口質量流量分別為2.022 4×10-3kg/s和1.305 2×10-3kg/s，其余參數見表2，數值模擬結果如圖3所示。

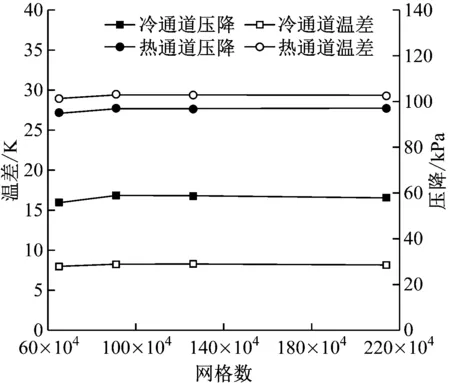
圖3 不同網格數下冷熱通道內的流動與傳熱特性

由圖3可知，在相同的工況條件下，冷熱通道中的壓降和溫差均隨著網格數的增加而變化，并在網格數超過91萬時基本趨于穩定，表明此時網格數增加對計算結果的影響可以忽略。因此，為提高計算效率，選用126萬網格方案進行數值模擬。

2.2 模擬準確性驗證

以Meshram等[20]的研究結果為參考標準，在相同的邊界條件下驗證所建物理模型的準確性，幾何模型采用半圓形直通道模型(即model1)。驗證結果見表3，其中誤差為(模擬值-參考值)/參考值。

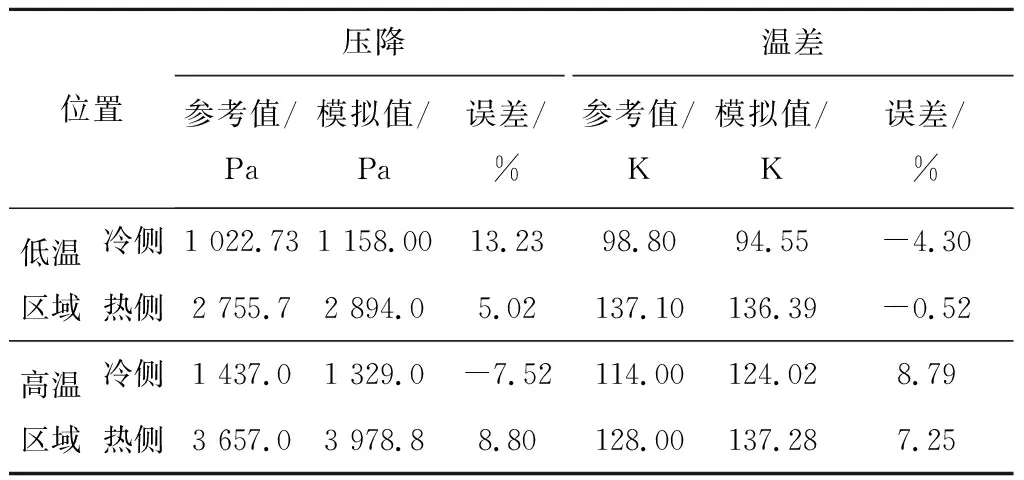
表3 模擬準確性驗證結果

由表3可知，數值模擬得到的冷熱通道內的壓降及溫差與參考值基本一致，壓降的誤差范圍為-7.52%～13.23%，溫差的誤差范圍為-4.30%～8.79%。綜上所述，所建立的冷熱通道換熱單元數學物理模型可以滿足S-CO2流動與傳熱特性數值模擬的準確性要求。

3 結果與分析

3.1 無格柵時直通道內S-CO2的流動與傳熱特性

首先研究了通道截面為半圓形(圖2(b))和矩形(圖2(c))時冷熱通道換熱單元中S-CO2的傳熱特性和流動阻力特性，Nu和f隨Re的變化情況如圖4所示。由圖4可知，當5 000≤Re≤30 000時，隨著Re的增大，無格柵的冷熱通道內Nu增大，而f則減小。這是由于當Re增大時，通道內流速升高、湍流加劇，增強了S-CO2與壁面之間的對流換熱，因而表現出更好的傳熱特性；同時，流速升高使得近壁面附近的層流邊界層變薄，通道中流動摩擦阻力相應減小。對比相同Re工況下的數值模擬結果不難發現，截面為半圓形的直通道傳熱性能較弱但流動摩擦阻力較小，而截面為矩形的直通道傳熱性能較好，但流動摩擦阻力較大。

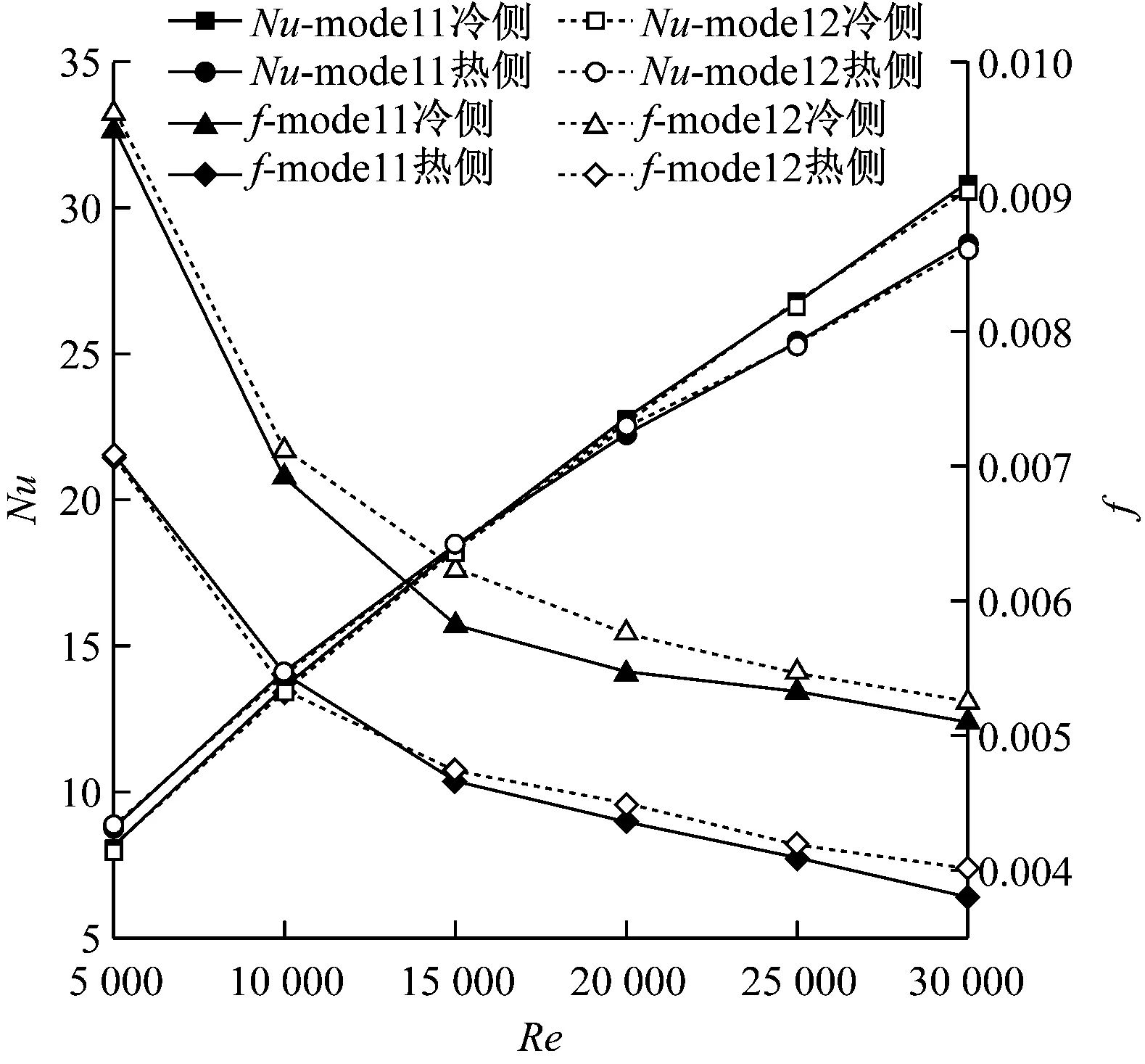
圖4 無格柵時直通道內Nu和f隨Re的變化情況

圖5給出了無格柵半圓形直通道PEC隨Re的變化情況。由圖5可以看出，當Re>5 000時，在無格柵情況下，半圓形冷熱直通道的PEC均略大于1，且在相同Re條件下，熱通道內流速大于冷通道內流速，因而熱通道的PEC均大于冷通道的PEC。此外，半圓形直通道內的PEC隨著Re的增大先升高后降低，當Re為25 000左右時，綜合傳熱效果最好。

圖5 無格柵半圓形直通道PEC隨Re的變化情況

綜上所述，半圓形直通道的綜合傳熱性能雖然優于矩形通道，但優勢并不明顯。因此，考慮到半圓形直通道加工工藝復雜、生產成本高昂，優化矩形通道結構、實現通道強化傳熱、提升綜合傳熱性能更具實際意義。

3.2 設置格柵時矩形通道內S-CO2的流動與傳熱特性

為了分析通道內熱流場情況，沿幾何模型Z軸方向選取了4個取樣面，取樣面與熱通道入口之間的距離分別為60 mm、175 mm、393 mm和508 mm，即第2個取樣面位于熱通道格柵下游3 mm處，第3個取樣面位于冷通道格柵下游3 mm處。圖6給出了Re為20 000時，3種擾流格柵設置方式對矩形通道內溫度分布的影響。由圖6可知，在相同Re條件下，熱通道內的溫度梯度大于冷通道內的溫度梯度，且對比Z=175 mm和Z=393 mm處的溫度云圖不難發現，熱通道內擾流格柵對溫度場的影響更加顯著。

圖6 矩形通道內不同位置處的溫度分布云圖

Fig.6 Contours of temperature distribution at different positions in the rectangular channel

此外，由圖2(b)可以看出，將擾流格柵設置在通道中部，對通道壁面處溫度邊界層的影響較小；而將擾流格柵設置在通道兩側，對通道壁面處溫度邊界層的影響則較大。將圖6(a)與圖6(d)、圖6(e)對比可知，S-CO2經過位于通道兩側的水平格柵后，其對側近壁處溫度邊界層變薄，近壁處流體與壁面之間的溫度梯度減小，實現了熱通道與冷通道之間的強化換熱，其中圖6(d)及圖6(e)同為兩側水平格柵模型，不同的是圖6(d)反映的是遠離水平格柵換熱界面處的溫度分布，圖6(e)反映的是緊靠水平格柵換熱界面處的溫度分布。考慮到湍動能是衡量流體混合能力的重要指標，冷熱通道內S-CO2在流經擾流格柵后湍動能會發生急劇變化，以熱通道為例，圖7給出了通道中心截面處3種擾流格柵設置方式對熱通道內S-CO2湍動能分布的影響。 以圖7(a)為比較基準可知，圖7(b)及圖7(c)中在通道中設置擾流格柵可以顯著增強流體擾動、促進流體混合，且圖7(d)中擾流格柵下游流體的湍動能峰值最高、湍動程度最強、湍動范圍最大。因此，將擾流格柵水平設置在通道兩側(即model5)時，擾流效果最好，可以有效改善近壁面流體與壁面之間的流動與傳熱。

圖7 矩形熱通道內S-CO2的湍動能分布云圖

Fig.7 Contours of turbulent kinetic energy distribution of S-CO2 in the hot rectangular channel

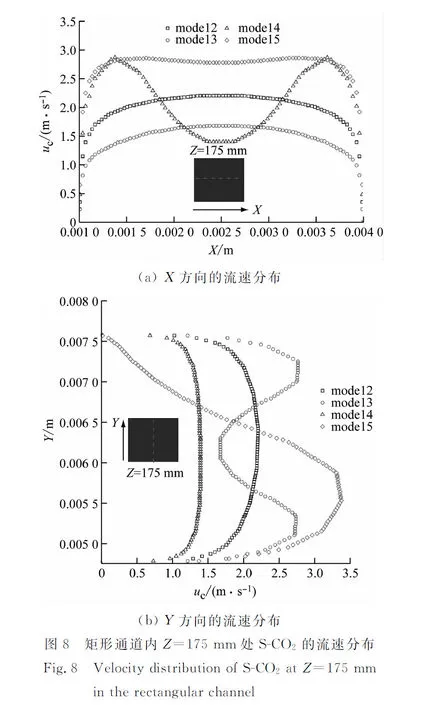
圖8給出了Z=175 mm處矩形熱通道內S-CO2的流速分布。由圖8可知，無格柵時矩形通道(即model2)內S-CO2在X方向和Y方向的流速分布均呈梯形狀，近似于管內完全發展的湍流流速分布；設置格柵后，隨著格柵設置方式的變化，矩形通道內S-CO2在不同方向的流速分布呈不同V形駝峰狀。在相同邊界條件下，將擾流格柵水平設置在通道兩側(即model5)時，矩形通道內S-CO2在X方向的平均流速和Y方向的峰值流速分別為2.71 m/s和3.38 m/s，均為最大值，可以有效促進流體換熱，但同時也會影響矩形通道內的阻力特性。

以無格柵矩形通道為比較基準，對比分析了不同格柵設置方式對通道內流動與傳熱特性的影響，如圖9所示。由圖9可知，在本文研究范圍內，設置格柵后矩形通道內的Nu隨著Re的增大而逐漸增大，而f則隨著Re的增大而逐漸減小，且隨著Re的持續增大，f的變化將趨于平緩，與圖4中無格柵時矩形通道內Nu和f隨Re的變化趨勢相同。此外，隨著Re的增大，矩形通道內的Nu/Nu0幾乎保持不變，f/f0則緩慢增大。當Re相同時，將擾流格柵水平設置在通道兩側(即model5)，Nu/Nu0和f/f0相對較大，這意味著該通道的傳熱性能較好，但流動摩擦阻力較大；將擾流格柵水平或者豎直設置在通道中部(即model3或model4)，Nu/Nu0和f/f0差別不大，此時矩形通道的傳熱性能較差，但流動摩擦阻力也較小。

為了綜合對比不同通道中的流動與傳熱特性，設置格柵后矩形通道內的PEC如圖10所示。由圖10可知，3種擾流格柵設置方式使得冷熱通道內部的PEC均小于1，且隨著Re的增大，PEC整體上呈緩慢下降趨勢。與無格柵的矩形通道相比，設置格柵后雖然可以增強傳熱，但同時也會增大流動摩擦阻力，導致綜合傳熱性能降低，且流速越高則綜合傳熱性能越差。因此，矩形通道內擾流格柵的優化設計需在保障強化傳熱的基礎上，盡可能降低對流動摩擦阻力的影響。對比圖6～圖10不難看出，在本文研究范圍內，將擾流格柵水平設置在矩形通道兩側的擾流效果最好，在單獨考慮傳熱特性時，其傳熱性能最優。因此，之后將在此基礎上，進一步探索擾流格柵間隔、個數以及形狀尺寸等因素對流動和傳熱特性的影響機理，實現通道綜合傳熱性能以及換熱器整體性能的優化。

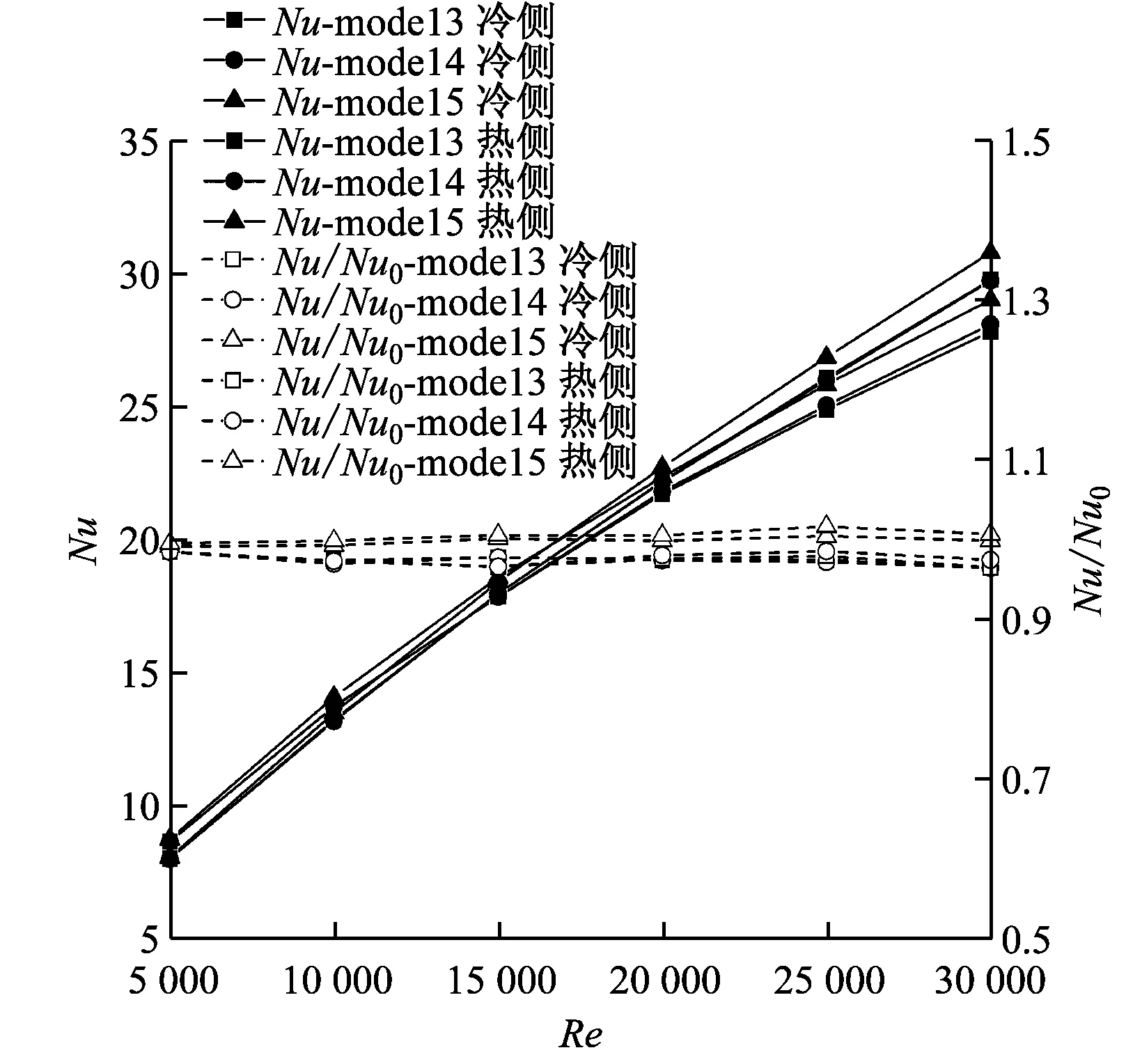
(a) Nu和Nu/Nu0隨Re的變化情況

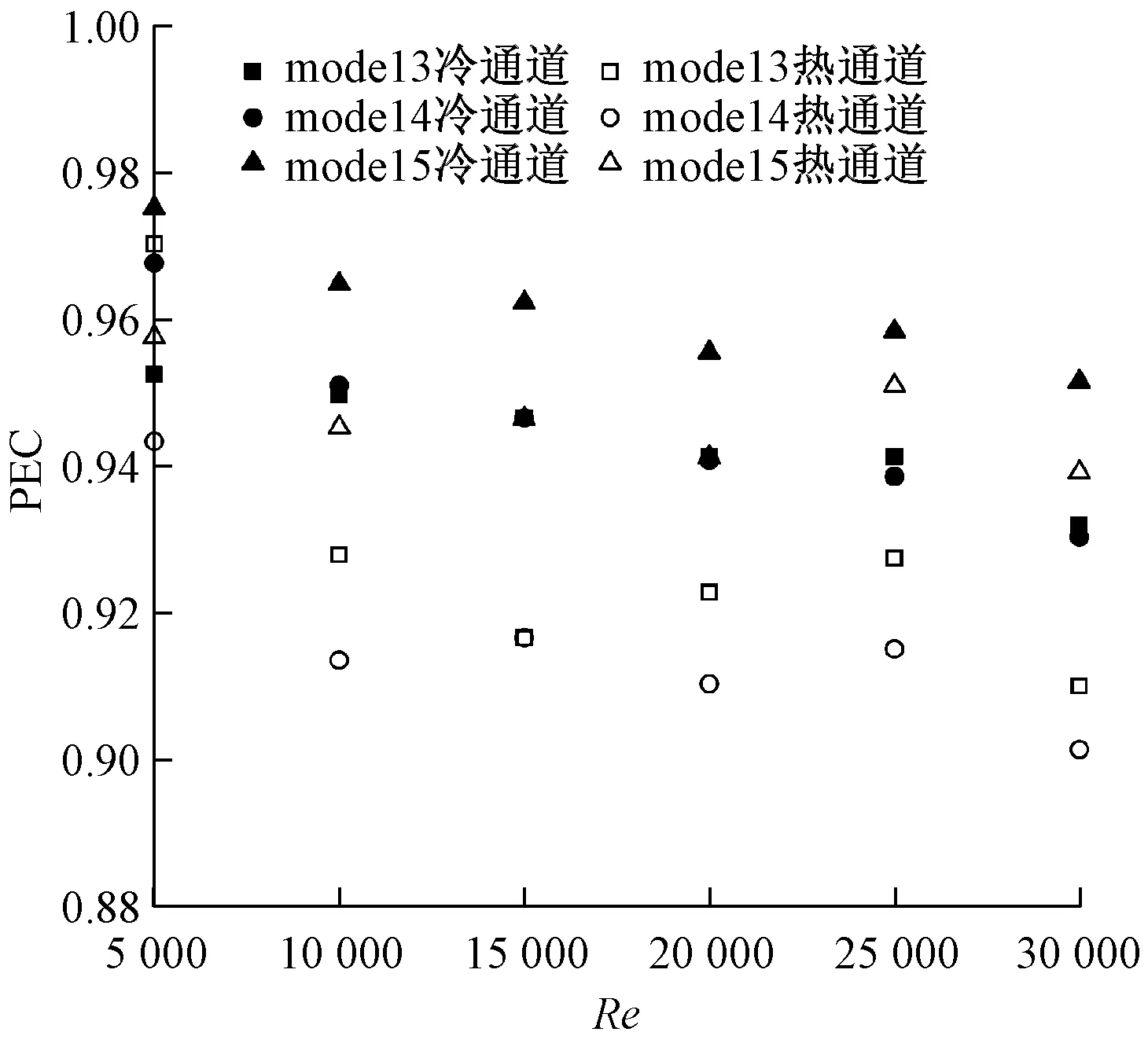
圖10 設置格柵后矩形通道內PEC隨Re的變化情況

4 結 論

(1) 隨著Re的增大，板式擴散焊矩形微通道換熱器換熱單元冷熱直通道內的S-CO2流速增大、湍流加劇，Nu隨之增大，f反而減小。

(2) 未設置擾流格柵時，與矩形通道相比，在相同Re條件下，半圓形直通道的傳熱性能較弱，同時流動摩擦阻力較小，綜合傳熱增強因子大于1，即相同當量直徑的半圓形直通道的綜合傳熱性能優于矩形通道。

(3) 設置擾流格柵后，在相同Re條件下，擾流格柵水平設置在矩形通道兩側時的擾流效果和傳熱性能最優，綜合傳熱性能相對最高。

(4) 與半圓形直通道和無格柵矩形通道相比，目前的擾流格柵設置方式在增強傳熱的同時會增大流動摩擦阻力，導致綜合傳熱增強因子降低。為兼顧換熱器流動與傳熱特性以及生產制造成本，需以擾流格柵水平設置在通道兩側的換熱單元為基礎，進一步深入探索擾流格柵的優化設計。