準周期響應對稱破缺分岔點的一種快速計算方法1)

龔冰清 鄭澤昌 陳衍茂 劉濟科

(中山大學理論與應用力學系,廣州 510275)

引言

周期或準周期振動,是非線性動力學系統出現的典型穩態響應[1-3].不同于周期振動,準周期響應不具有固定的振動周期,狀態變量不再按某周期有規律地重復出現.更具體地說,準周期振動的特征是其振動頻率由多個不可公約的頻率線性組合而成[4-6].因而,這些不可約的頻率也被稱為基頻,由不可約頻率線性組合而成的準周期頻率稱為組合頻率.

在不同的非線性系統中,準周期響應出現的機制機理也不盡相同.出現準周期響應的系統類型也是多種多樣,例如,受到多不可約頻率外激勵作用的系統[7]、非線性耦合導致的模態共振[8]以及參數激振與自激振動之間的耦合[9]等情況都可能產生準周期響應.從振動的頻率成分看,準周期振動可以看作是不可公約頻率之間的耦合效應,而引起的復合響應.在實際工程中,準周期振動在各種科學和工程問題中均被大量報道,例如機械工程[10]、電子工程[11]、氣動彈性[12]等領域.

在求解方面,數值方法由于簡單明了且易于實現,因此被廣泛運用于準周期響應的求解[13-15].這類基于時間離散的時程響應跟蹤數值算法,一般無法直接獲得系統的不穩定穩態解,即不穩定的周期或準周期響應.因為,不穩定解意味著微小的擾動或誤差會使得解出現越來越大的偏差,從而偏離不穩定解本身.眾所周知,系統的分岔通常會伴隨著某些解的穩定性改變.為了進一步研究系統響應的分岔現象,研究人員提出了基于Fourier 級數展開的半解析半數值計算方法,用于求解周期響應,例如諧波平衡法[1]和增量諧波平衡IHB 法[16-19]諧波展開類方法、L-P 法和多尺度法等攝動類方法[1]、平均法和KBM 法等漸進方法[1]以及同倫分析法[20]等.這些方法有的也被改進或推廣、用來求解準周期響應,其中多時間尺度IHB 法可以計算強非線性、多自由度系統,獲得了廣泛的應用.

關于系統的平衡點和周期解的分岔問題,目前已有大量的研究和成熟的理論,例如Hopf 分岔定理[21]和Floquet 理論[22]等.相較于平衡點分岔,周期響應的分岔計算是一個更加棘手的問題.20 世紀80 年代,陳予恕[1]提出了周期響應分岔計算的C-L 方法,并在諸多科學和工程中的非線性系統中得以廣泛應用.在IHB 法中,若引入諧波系數限制增量過程,可直接求解周期響應倍周期分岔或對稱性破缺的臨界值[23].

對于準周期響應,其分岔計算方法和分析理論就更加棘手,也更加缺乏.目前來看,對于非線性動力系統的準周期響應,在大多數情況下,其分岔點的確定是通過反復的數值模擬來實現的.這種方法的原理簡單、過程直接,但一方面計算量往往很大,另一方面如前面所述、數值方法也無法提供不穩定的解,而且存在不利于分析參數的影響規律等問題.為此,本文將周期響應對稱破缺分岔計算方法[23]進一步推廣,使之對于準周期同樣有效,該方法是基于增量諧波平衡過程的.利用多時間尺度的IHB 法,設計迭代格式,通過追蹤特定的諧波系數,從而快速求解準周期響應對稱破缺分岔點.以多頻激勵Duffing系統以及Duffing-van der Pol 耦合系統為例,闡述方法的主要步驟,驗證方法的正確性和有效性.

1 增量諧波平衡法

增量諧波平衡法是求解非線性振動問題的一種半數值、半解析方法,是由Lau 等[24]在20 世紀80 年代提出并發展起來的.IHB 法的本質是Newton-Raphson 增量過程和諧波平衡過程的結合[25].經過了幾十年的發展,IHB 不僅可用于周期或準周期響應的求解,已應用于動力學響應分析的諸多領域,如混沌控制[26]、反問題識別[27]等.

考慮含不可約頻率雙外激勵的非線性振動系統

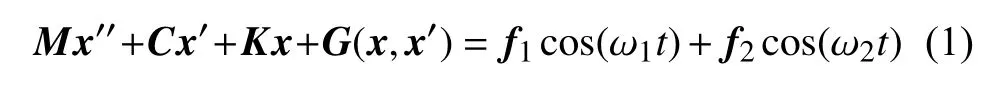
其中M,C,K分別是質量、阻尼和剛度矩陣,G(x,x′)是非線性函數.f1和f2是外激勵向量幅值,ω1和 ω2是外激勵的不可約頻率.不失一般性,將參數 ω1作為分岔控制參數.

IHB 法的第一步是增量過程,即Newton-Raphson 過程.讓xi表示一種振動狀態,對應的控制參數為 ω1=ω1i,其臨近狀態可以通過增量的方式表示為

將式(2)代入式(1),展開并忽略高階小量,得到線性化的增量方程

其中

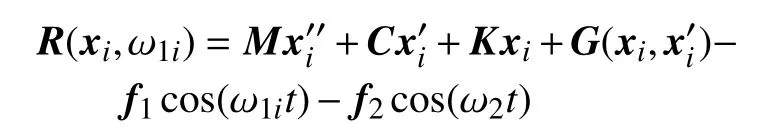
稱為不平衡力,當xi和ω1i為方程(1) 的精確解時,R(xi,ω1i)=0.

IHB 法的第二步是諧波平衡過程,也即Ritz-Garlerkin 平均過程,令

把式(4)和式(5)代入式(3),并應用諧波平衡過程,可以得到線性方程組

其 中 ?u=[?c0,?c10,?s10,···,?cMN,?sMN]T,方 陣Ku是 (M+N)(M+N+1)+1 維的雅可比矩陣,Kω是控制參數的梯度向量,KR是剩余向量.這些矩陣和向量可通過初始解xi和 ωi確定.在IHB 法中,通常應選擇一個主動變化的參數(稱為主動增量)來控制解的連續延拓.如果 ? ω 被給出,方程(6)描述的每一步增量為 ?u的一組方程,可以迭代求解.

2 對稱破缺分岔點的快速算法

下面引入補充方程,并將 ? ω 看成被動增量參與迭代,進而獲得系統發生對稱性破缺的分岔值.作為一般性的討論,可將準周期解嚴格表示為廣義的Fourier 級數

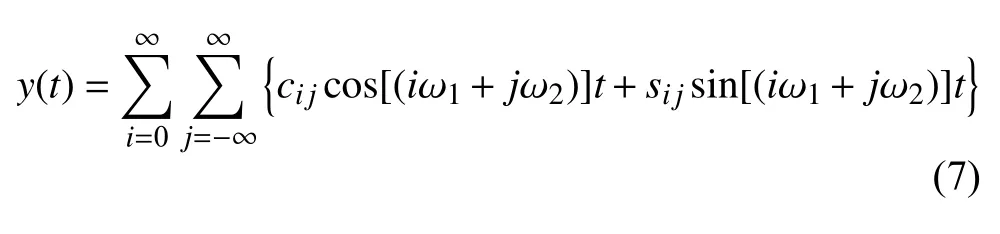
其中y(t)也可作為x(t)的一個分量.在實際計算中,對于單自由度系統,y(t)即是x(t);對于多自由度系統,y(t)可取為x(t)的第一個分量.對稱的準周期響應的相圖指的是,對于任意一點 (y(t),y′(t)),總能找到關于原點與之對稱的點 (?y(t),?y′(t)).也即是表明,如果y(t) 是方程(1)的解,那么 ?y(t) 也是一個解.

引入雙時間尺度 τ1=ω1t和τ2=ω2t,和周期解對稱性質類似[23],對于關于原點對稱的準周期解,其對稱性由以下等式描述

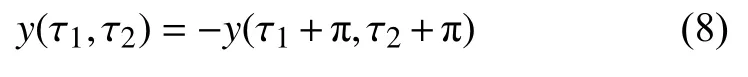
由式(7),可知

根據方程(7)～方程(9)可知,當i+j為奇數時,對稱條件自然滿足;當i+j為偶數時,若要滿足對稱條件,則意味著

注意到i+j的奇偶性和 |i|+|j| 相同.那么,當偶次諧波系數取到非零的小量時,準周期解便失去對稱性,也可以看成是系統發生對稱破缺分岔的臨界狀態.為此,在迭代格式(6)中,補充方程

其中 0 <λ0?1,那么通過迭代過程,構造以下迭代格式

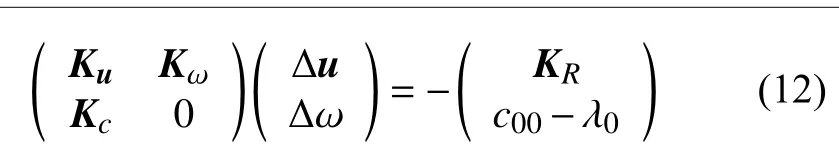
其中Kc=(1 0 ··· 0) 是補充方程(11) 關于諧波系數的Jacobi 矩陣.只要 λ0足夠小時,便可以近似確定關于參數 ω1的對稱破缺分岔點.理論上,λ0越小則 ω1越可能接近真實的分岔值.在實際計算中,可以取 λ0為非常小的正數,例如λ0=1.0×10?8等.當然,最終的近似程度也還受到解的截斷諧波系數的影響.這點在下面的算例部分將予以討論.

3 結果驗證與討論

首先,考慮含不可約頻率雙外激勵的Duffing 振子系統[20,28-29]

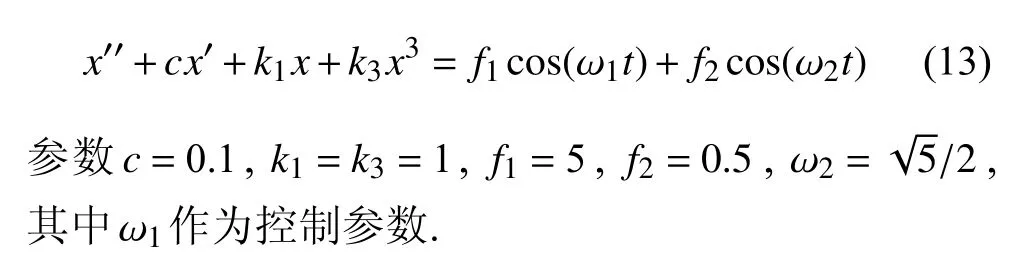
圖1 是所考慮Duffing 系統的準周期響應相圖,其中圖1(a1)～圖1(c1)為IHB 法結果,圖1(a2)～圖1(c2)為4 階Runge-Kutta (RK)法結果.在求解過程中,IHB 解截取了最高階M+N=10 階諧波,數值解采用了IHB 解作為初始條件,通過RK 法積分獲得.準周期解的穩定性判別目前還是一個非常棘手的問題.一般的數值積分方法如RK 法和Newmark 法等無法追蹤不穩定解,通過這一直觀特點簡單判斷解的穩定性.分別對比圖1(a1)、圖1(a2)(ω1=0.8)及圖1(c1)、圖1(c2)(ω1=1),IHB 結果與RK 結果是完全吻合,說明這些準周期解都是穩定的.進一步觀察到,在圖1(a1)中,準周期響應相圖是關于原點中心對稱的,因此是對稱的.

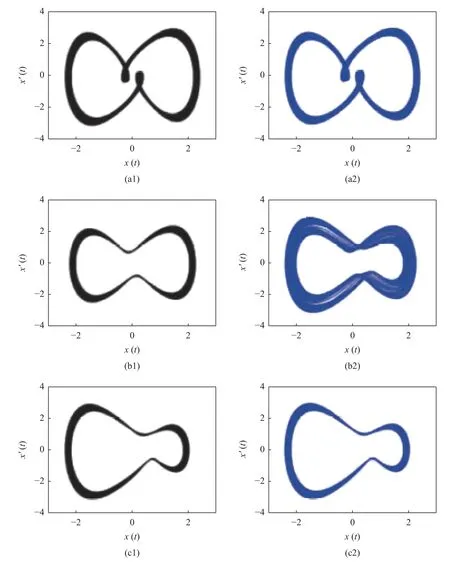
圖1 Duffing 系統(13)準周期響應相圖,(a1) ω1=0.8,穩定IHB 法解;(b1) ω1=1.0,不穩定的IHB 法解;(c1) ω1=1.0,穩定的IHB 法解;(a2),(b2),(c2)為相應的RK 數值解.其中,IHB 法的截取諧波數為 M+N=10Fig.1 The quasi-periodic responses of Duffing system (13).(a1) Stable with ω1=0.8,(b1) unstable with ω1=1.0 and (c1) stable with ω1=1.0,all obtained by the IHB method with the truncated number of harmonics as M+N=10 ;(a2),(b2),(c2) the corresponding solutions provided by the RK method

當 ω1=1.0 時,而圖1(b1),圖1(b2)中的結果并不完全相同.其中,由IHB 法解作為初始值所得的RK法結果(圖1(b2)所示),從對稱的IHB 法解(圖1(b1)所示)開始,逐漸收斂到另一個非對稱的準周期解,即圖1(b2)所示非對稱部分.實際上,圖1(b2)所示的非對稱部分、在相圖上和圖1(c1)及圖1(c2)所示解是一樣的.IHB 法是半解析半數值方法,可以得到不穩定的對稱準周期解和穩定的非對稱準周期解.由此可知系統在參數范圍 0.8<ω1<1.0 發生了對稱破缺分岔,且對稱的準周期解失去了穩定性.

為準確找到系統發生對稱破缺的分岔點,根據上述方法,將 λ0逐步減小,得到收斂結果,其中 ω1的變化如圖2 所示.隨著 λ0的取值越來越小,ω1的值也逐漸收斂.當諧波數取M+N=8 時,可以計算得到分岔值約為0.933 02,當諧波數取M+N=10 時,可以計算得到分岔值約為0.937 58.

圖2 采用不同的 λ0 所對應的對稱破缺分岔點Fig.2 The symmetry breaking point predicted by the presented method with different value of λ0

圖3 是由IHB 法獲得的Duffing 系統準周期響應的分岔圖.在P點(約為 ω1=0.935)附近,對稱的準周期解產生非對稱的分支.此時,系統出現了對稱破缺分岔現象.和周期解分岔類似,經歷了分岔后、準周期解也一般會穩定性改變.周期解的穩定性一般可通過經典的Floquet 理論準確判別[1].然而,對于準周期解,其穩定性判別是一個相當棘手的問題.為此,通過分析系統穩態響應的相圖變化,如圖1 所示,進而直觀地判別IHB 法所得結果的穩定性.研究發現,對稱準周期響應由于對稱破壞而失去穩定性,同時出現的非對稱解是穩定的.

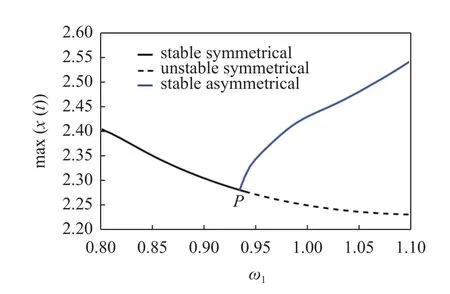
圖3 由IHB 法獲得的Duffing 系統(13)準周期響應分岔圖,其中P 為對稱破缺分岔點Fig.3 The bifurcation chart of the quasi-periodic response of Duffing system (13),where P denotes the symmetry breaking point

進一步,用數值法驗證準周期響應對稱破缺的發生.圖4 給出由RK 法得到的解的最大和最小振幅隨 ω1的變化圖.可以觀察到,在 ω1=0.937 5 前,準周期解的最大值和最小值完全重合,即解是對稱的;而隨著 ω1增大,最大值和最小值之間逐漸出現差值.也即是表明,系統已經失去了對稱性,并且大約在ω1=0.937 5 時發生了對稱破缺分岔.這也與IHB 法結果基本是一致的.

圖4 RK 法所得Duffing 系統(13)穩定的準周期解的最大和最小振幅變化圖Fig.4 The maximal and minimal of the amplitude of the stable quasiperiodic response of Duffing system (13),provided by the RK method

圖5 給出了分別由快速Fourier 變換和IHB 法獲得的準周期響應頻譜圖.首先,IHB 法結果和數值結果吻合良好.數值結果的部分峰值沒有IHB 法結果與之對應,因為IHB 法中組合諧波進行了截斷,取了M+N=7,即 |i|+|j|≥8 的組合諧波沒有包含在IHB 法結果中.當參數取 ω1=0.937 時,圖5(a)所示,響應只包含奇數次諧波成分.對應于解的表達式(7),出現了當 |i|+|j| 是奇數(即1,3,5,7 等)時的若干諧波成分.當參數為 ω1=0.938 時,除了占主要部分的奇數次諧波之外,還出現了幅值較小的偶數次諧波,圖5(b)所示的 2 ω1,即i+j=2.圖6 是準周期響應的頻率譜瀑布圖,由此可更直觀地觀察到,當參數 ω1逐漸增加,響應出現了偶次諧波成分.根據基于關系式(8)～式(10)的討論,偶數次諧波分量的出現,表明準周期響應逐漸失去了對稱性.由此推斷,對稱性破缺分岔點出現在0.937 和0.938之間.

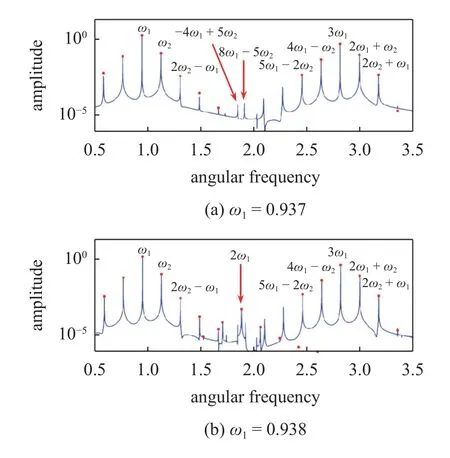
圖5 由快速Fourier 變換得到的Duffing 系統(13)準周期響應的頻譜圖,其中藍線是數值方法結果,紅點是IHB 法結果,組合諧波截斷數為 M+N=7Fig.5 The FFT spectrum for the quasi-periodic response of Duffing system (13),where the blue line denotes the numerical result and red the IHB result,with the number of truncated harmonics as M+N=7

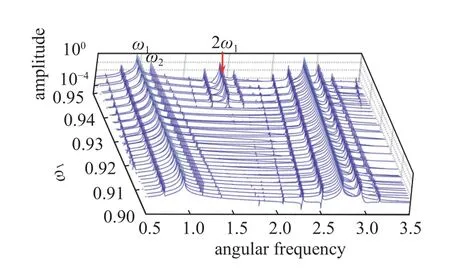
圖6 Duffing 系統(13)準周期響應的頻率譜瀑布圖Fig.6 The frequency waterfall for the quasi-periodic response of Duffing system (13)

Duffing 系統和van der Pol 系統都是典型的非線性振動系統.由它們耦合組成的多自由度系統,更是蘊含了豐富的動力學行為,是非線性研究廣泛采用的模型之一[30-31].為了進一步檢驗所提方法的有效性,考慮Duffing-van der Pol 耦合振子

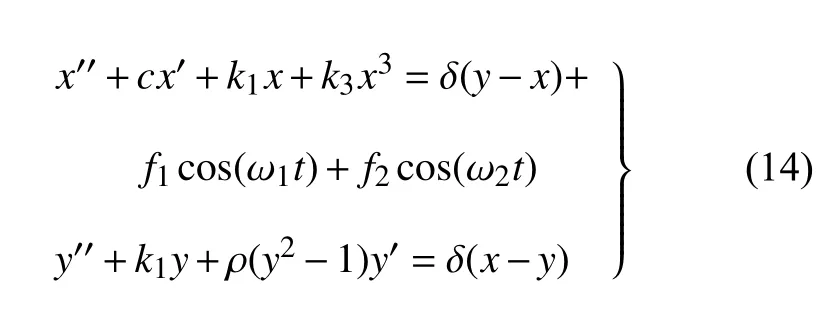
其中,Duffing 振子受雙諧波外激勵,參數選擇和系統(13)相同;耦合系數取 δ=0.2 ;ρ=1 是van der Pol振子的非線性系數.

對于含強非線性環節的van der Pol 系統,一些依賴于小參數的攝動類方法有時難以獲得準確的周期或準周期解.由于不依賴于小參數,IHB 和同倫分析等方法對含van der Pol 振子的強非線性系統有效,因而被廣泛采用[20,31-33].

圖7 給出了本文算法所得的分岔值與預設小量λ0之間的關系.當 λ0逐漸減小時,所得分岔值快速收斂于固定值,約為1.000 4.圖8 所示準周期響應的最大和最小振幅,當 ω1超過1 且接近1.001 時,最大和最小振幅出現了微小的偏差.這表明,在此參數區間,響應逐漸失去了對稱性,也即是出現了對稱性破缺分岔,驗證了計算結果的準確性.

圖7 Duffing-van der Pol 系統(14)的對稱破缺分岔值關于 λ0 的收斂圖,其中截取諧波數為 M+N=8Fig.7 The symmetry breaking point predicted by the presented method with different value of λ0,with the number of truncated number of harmonics as M+N=8 for Duffing-van der Pol system (14)

圖8 RK 法所得Duffing-van der Pol 系統(14)準周期解的最大和最小振幅Fig.8 The maximal and minimal of the amplitude of the stable quasiperiodic response of Duffing-van der Pol system (14),provided by the RK method

4 結論

本文基于IHB 法,提出了一種快速計算準周期響應對稱破缺分岔的方法.方法的基本依據是,當發生對稱破缺分岔前,準周期響應的某些諧波系數為0;發生分岔的過程中,這些系數逐漸變為非0 的小量.那么,依據這一性質,在IHB 法迭代格式中,預先令某個諧波系數為給定的小量,可以將控制參數視為被動變量,通過收斂的IHB 法結果,直接獲得響應的分岔值.

研究了含不可公約頻率雙外激勵Duffing 振子系統、以及Duffing-van der Pol 耦合系統,驗證了所提方法.結果表明,方法能準確得到系統準周期響應的對稱破缺分岔點,得到了數值法結果的驗證.本文方法不僅可以找到不穩定解,更重要的是可以直接提供控制參數,而不需要反復的跟蹤和試錯過程.