初中數(shù)學“規(guī)律探索型概念課”的教學誤區(qū)及改進措施
——以《銳角三角函數(shù)》概念課為例

許家健

(廣東省陽江市江城區(qū)教師發(fā)展中心 529900)

在初中數(shù)學概念課教學中，有一類屬于“規(guī)律探索型概念課”.筆者曾在三所不同的學校聽了題為“銳角三角函數(shù)”的同一節(jié)概念課，這節(jié)課就屬于“規(guī)律探索型概念課”.現(xiàn)對這三節(jié)課的教學誤區(qū)進行簡要分析，并提出一些改進措施.

1 初中數(shù)學“規(guī)律探索型概念課”的教學誤區(qū)

1.1 采用“概念講述”的方式進行教學，學生沒有經歷概念的形成過程，死記硬背概念，不會靈活運用

學校1的老師直接采用了“概念講述”的方式進行教學，大致流程如下：

(1)屏幕顯示課本的問題：為了綠化荒山，某地打算從位于山腳下的機井房沿著山坡鋪設水管，在山坡上修建一座揚水站，對坡面的綠地進行噴灌，觀測得斜坡的坡角為30°，為使出水口的高度為35m，需要準備多長的水管？

(2)老師講解：上面的問題可以用圖形表示為：在Rt△ABC中，∠C=90°，∠A=30°，若BC=35m，求AB的長.

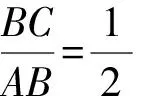
(4)給出正弦定義，然后讓學生讀定義.

(5)例題講解，如圖1，在Rt△ABC中，∠C=90°，求sinA和sinB.

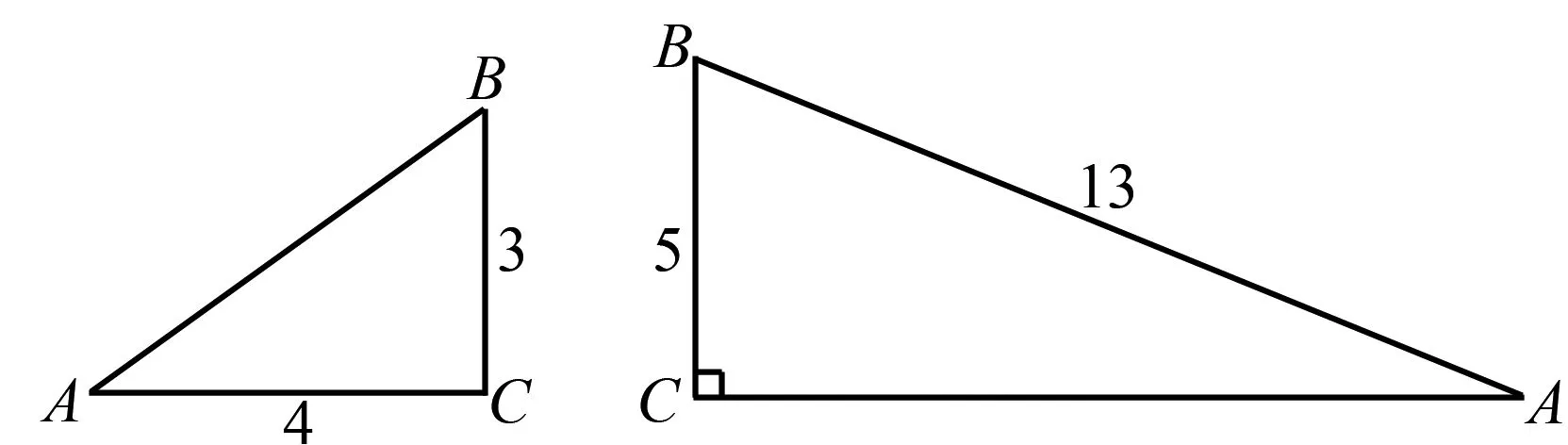
圖1

(6)設計幾道練習題，讓學生鞏固概念.

通過這樣的方式學習，學生并沒有真正理解“正弦”概念的含義.課后，筆者對學生問了幾個問題，學生只記住了對邊與斜邊的比，并不知道這個比值是由角的大小確定的，更不理解這個比值是隨角的大小變化而變化的函數(shù)關系，若把直角三角形變成銳角三角形就更無從下手了.

1.2 只重視對已有結論的證明，忽視了對結論的猜想和發(fā)現(xiàn)

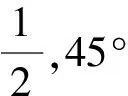
在上述過程中，老師從特殊到一般，對結論進行了證明，過程看似完整.事實上，學生仍處于被動的學習狀態(tài)，充其量只學會了證明他人發(fā)現(xiàn)的結論，卻沒有經歷“發(fā)現(xiàn)”的過程，沒有學會如何去發(fā)現(xiàn).

1.3 從局部到局部的散點狀教學，概念關聯(lián)不強

學校3的老師基本上按照教材的編排順序進行正弦概念的教學，簡要概括流程如下：

問題1 顯示課本中的為了綠化荒山，建揚水站的問題.

問題2 在上面的問題中，如果出水口的高度為50m，那么需要準備多長的水管？

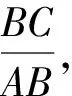
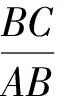
這樣的設計是一種典型的從局部到局部的散點狀教學，概念關聯(lián)不強，學生要等學完余弦、正切等概念后才給出銳角三角函數(shù)的概念，學習中缺少類比聯(lián)想的過程，也不能從整體上理解函數(shù)的概念.

2 初中數(shù)學“規(guī)律探索型概念課”的教學模式分析及舉例

2.1 初中數(shù)學“規(guī)律探索型概念課”的教學模式分析

作為過程的數(shù)學概念，只有經歷概念完整的形成過程，學生對數(shù)學概念內涵的理解才會更加清晰準確，才會更加豐富.作為對象的數(shù)學概念，我們必需克服散點狀的教學形式，要有整體觀念，使學生對概念的理解有一種結構化的認識，加強數(shù)學概念之間的聯(lián)系.針對初中數(shù)學“規(guī)律探索型概念課”的特點，我們應采取如下的教學模式：材料感知→描述與反思、發(fā)現(xiàn)猜想→證明猜想、歸納結論→概念命名→練習鞏固、納入系統(tǒng).

2.2 “銳角三角函數(shù)概念課”教學過程設計及分析

環(huán)節(jié)一 復習舊知

問題1 在Rt△ABC中，∠C=90°，∠A=20°，求∠B.

問題2Rt△ABC中，AB=3，BC=4，求AC.

環(huán)節(jié)二 材料感知，情境引入

問題3 顯示課本中的為了綠化荒山，建揚水站的問題.

老師提問：問題1涉及了直角三角形角和角之間的關系，問題2涉及了直角三角形邊與邊之間的關系，問題3涉及直角三角形哪些要素之間的關系？

設計目的：讓學生從生活中的具體例子出發(fā)，抽象出數(shù)學問題，培養(yǎng)學生數(shù)學建模的思想，激發(fā)學生的學習興趣；從復習直角三角形角與角的關系、邊與邊的關系，再到本節(jié)邊與角的關系，過渡自然，也引導學生對直角三角形各元素進行整體研究和認識.

環(huán)節(jié)三 描述與反思、發(fā)現(xiàn)猜想

說一說問題4 在Rt△ABC中，三條邊兩兩組合，一共有多少個比值？

做一做問題5 填表1(Rt△ABC，∠C=90°)

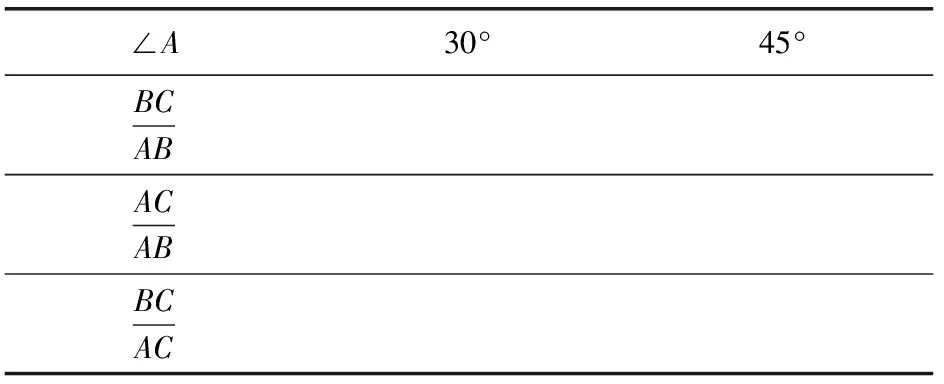
表1

設計意圖：這一環(huán)節(jié)，我們通過豐富的材料，讓學生參與對這些材料的比較、辨析活動，從角與角、邊與邊的關系自然想到對邊與角關系的研究.

猜一猜先讓學生分小組對前面的活動進行描述與反思，進而提問：當∠A=30°或45°時，上述表格里的三個比值是固定的，若銳角∠A取其他數(shù)值時，上述比值有什么變化？你是怎樣研究的？由此，你得出什么樣的猜想？

當學生產生爭辯時，老師提議：可否用幾何畫板驗證一下？驗證后填表2：

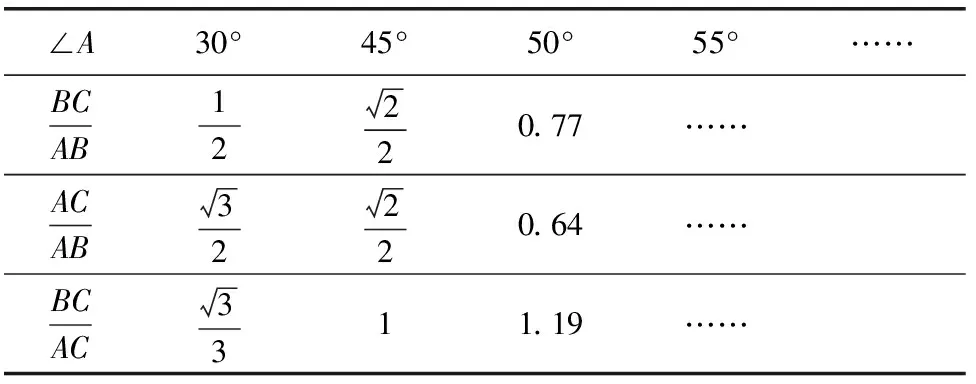
表2

通過描述、反思、實驗，引導學生取得一致猜想.

環(huán)節(jié)四 證明猜想，歸納結論

操作：作任意∠A，在∠A的一邊上任意取一點B，作BC垂直于∠A的另一邊，垂足為C，在射線AB上取不同于B的另一點B′，作B′C′⊥AC，交點為C′.

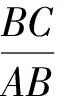
設計意圖：這個操作設計可以由學生自主完成，若學生在證明猜想時感到困難，老師可以利用幾何畫板的動態(tài)展示啟發(fā)學生思路，同時讓學生經歷從不完全歸納到演繹推理的過程，既培養(yǎng)了思維的發(fā)散性，又培養(yǎng)了思維的嚴謹性.

環(huán)節(jié)五 概念命名，引入符號

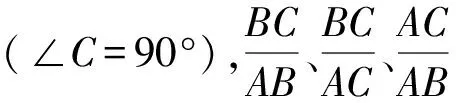
設計意圖：這種設計是在尊重教材原有設計的基礎上，進一步開發(fā)課程資源，在適合學生實際情況的前提下，對教材進行重組，先讓學生重溫“函數(shù)”的概念，接著理解“三角函數(shù)”，最后到“正弦”、“余弦”、“正切”.這種從整體到局部的設計，加強了概念之間的關聯(lián)，有利于學生對“三角函數(shù)”概念的結構性理解.

環(huán)節(jié)六 練習鞏固，納入系統(tǒng)

(1)基本練習及變式練習

(2)引導學生小結與反思：今天你有什么收獲？你知道“函數(shù)”、“三角函數(shù)”、“正弦”、“余弦”、“正切”各概念之間有什么區(qū)別和聯(lián)系嗎？你可以用思維導圖表示上述關系嗎？

設計意圖：通過基本練習及變式練習，讓學生在應用中進一步加深對“銳角三角函數(shù)”概念的理解；通過小結與反思，讓學生把“銳角三角函數(shù)”概念納入已有的知識系統(tǒng).

在這類概念課的教學中，一定要讓學生經歷完整的概念探索過程，學生才能對數(shù)學概念有更深度的理解，學生的數(shù)學素養(yǎng)才能真正養(yǎng)成，數(shù)學概念教學的價值才能真正實現(xiàn).