具有Robin邊界的壞死核非線性腫瘤生長模型整體解的存在性*

吳 攸

（廣東工業大學數學與統計學院，廣東 廣州 510520）

0 引 言

腫瘤生長規律的數學研究，很早就引起了人們的重視 .早在 20 世紀 70 年代，Greenspan［1］考慮了腫瘤內營養物質的反應擴散和由此導致的腫瘤細胞的繁衍與死亡，首先用偏微分方程自由邊界問題來描述腫瘤的生長.由于腫瘤所占據的空間區域和邊界是隨時間不斷變化并且不是預先給定的，需要與其他未知函數一起確定，所以自20世紀90年代末以來，這一課題引起了以國際著名偏微分方程專家和應用數學家Friedman院士為代表的一批偏微分方程工作者的極大興趣，其研究在過去20多年中取得了長足的發展，并涌現出了眾多出色的研究成果，已成為偏微分方程研究領域的一個新的熱點研究課題.

Byrne 和 Chaplain［2］提 出 了 關 于 腫 瘤 生 長 的Byrne-Chaplain模型，該模型的邊界條件包括Dirichlet自由邊界和Robin自由邊界，根據模型中是否包含壞死核，可以將模型進一步細分為有壞死核的腫瘤生長模型和無壞死核的腫瘤生長模型；Fried‐man 和 Reitich［3］研究了 Dirichlet自由邊界條件下的無壞死核的腫瘤生長模型，得到了整體解的存在唯一性以及解的漸近性態；Cui和 Friedman［4］研究了Dirichlet自由邊界條件下的有壞死核的腫瘤生長模型，得到了解的適定性以及解的漸近性態；Friedman和Lam［5-6］研究了Robin自由邊界條件下的無壞死核的腫瘤生長模型，得到了穩態解的存在唯一性，并對解的漸近性態進行了討論；Shen和Wei［7］研究了Robin自由邊界下的無壞死核的腫瘤生長模型，得到了整體解的存在唯一性以及解的漸近性態；沈海雙等［8］研究了Robin自由邊界條件下的有壞死核的腫瘤生長模型，得到了穩態解的存在唯一性.上述文獻所研究的模型中，描述營養物濃度和抑制物濃度的函數均為線性函數.在基于生物學和醫學實際的前提下，衛雪梅和崔尚斌［9-10］進行了腫瘤生長模型包含非線性函數的研究，并得到了模型整體解的存 在 唯 一 性 和 漸 近 性 態 ；Cui［11］、Wei［12］、Wu 和Wang［13］、Bueno 等［14］研究了有壞死核的非線性腫瘤生長模型在Dirichlet自由邊界條件下解的適定性；Zhuang 和 Cui［15］研究了 Robin 自由邊界下無壞死核的非線性腫瘤生長模型，得到整體解的存在唯一性；Zheng 和 Cui［16］研究了 Robin 自由邊界下無壞死核的非線性腫瘤生長模型解的漸近性態.

事實上，對于有壞死核的腫瘤生長模型而言，其生長可以分為2個階段，假設σD為腫瘤細胞是否壞死的閾值，即當σ＞σD時，所有的腫瘤細胞存活；當σ≤σD時，所有的腫瘤細胞壞死.本文在前述文獻［7，9-11］的基礎上把 Dirichlet自由邊界改為 Robin 自由邊界條件下的有壞死核的非線性腫瘤生長模型進行研究，具體模型如下：

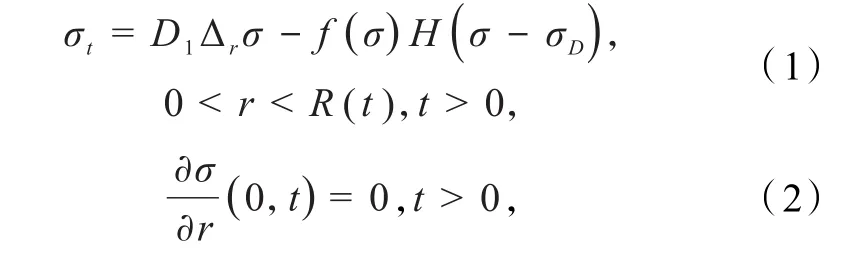
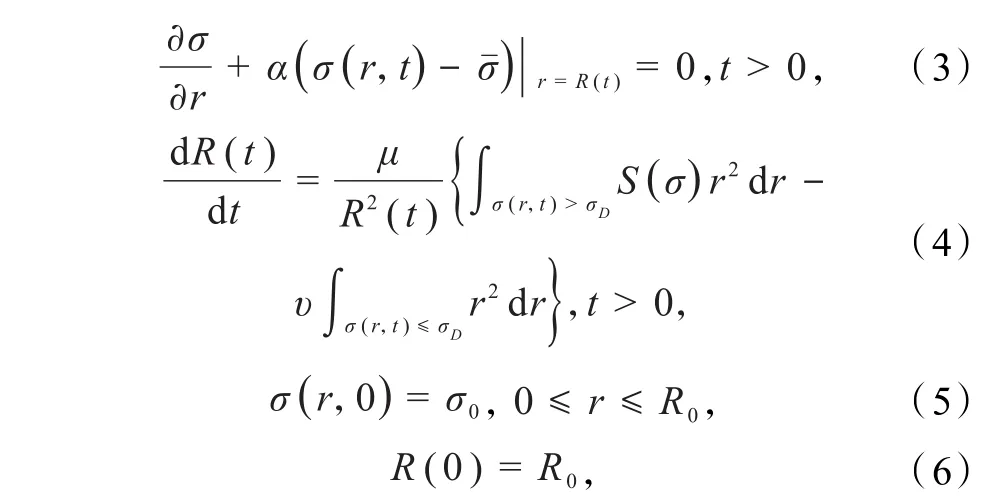
在符合生物學和醫學原理的前提下，本文做出如下假設：（A1）f(σ ) =σf1(σ)，其中f1(σ)為定義在[ 0 ，∞ ]上的函數且滿足Lipschitz連續，當 σ ≥0時，有f1(σ )≥0恒成立；（A2）S是定義在[0 ，∞ ]上的函數 ，且 滿 足 Lipschitz 連 續 ；（A3）σ0∈ W3，∞(0，R0)，，其 中

本文對于模型中的不連續函數進行近似逼近的方法，主要是參考 Zheng 和 Cui［16］對 Dirichlet自由邊界條件下的有壞死核的非線性腫瘤生長模型整體解的存在性的證明中所使用的方法，即構造光滑函數進行逼近.再結合Schauder不動點定理和拋物方程的Lp理論，最終能夠得到Robin自由邊界下有壞死核的非線性腫瘤模型整體解的存在性.

本文的主要結論如下：

定理 1.1 在假設（A1）、（A2）、（A3）的條件下，對于任意的T ＞0，問題（1）～（6）存在解(σ (r ， t)，R(t))，且解 σ(r ， t) 滿足：

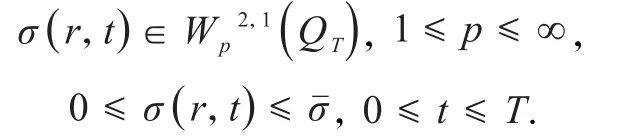
1 預備引理

2 自由邊界問題的轉換

3 逼近問題解的存在性

4 原模型整體解的存在性

在證明了式（21）～（24）在XT上解的存在性之后，接下來對式（1）～（6）在XT上整體解的存在性進行證明，即證明本文主要定理1.1.首先證明如下定理.

再結合式（37）和（42）可以得到

將式（42）和（43）代入式（38）～（41）中，可得式（16）～（19）存在解v=v(z ， t)，即結論得證 .

由引理2.1可知，自由邊界問題式（1）～（6）與固定邊界問題式（16）～（19）等價，結合定理4.1，可得式（1）～（6）整體解的存在性，即定理1.1得證.

5 結束語

本文研究了一個Robin自由邊界條件下的有壞死核的非線性腫瘤生長模型，通過對模型中的不連續項進行逼近，證明了模型逼近解的存在性，從而得到原模型整體弱解的存在性.本文是用弱收斂的方法得到原模型弱解的存在性，而弱解的唯一性目前尚未得到，這是一個很困難的問題，希望將來可以找到方法得到弱解的唯一性.