基于機器學習BP算法和樹模型算法的井筒流體流型預測

＊張怡然 李奧

（長江大學地球物理與石油資源學院 湖北 430100）

引言

為了使油氣生產更加科學化、高效化，對測井方案的設計是進行生產測井前的關鍵環節，設計環節中需要選取合適的測井儀器，估算產量，對井下流體進行流型判斷等。其中，對井下流體流型的判斷是非常重要的步驟，流體流型判斷直接關系到后續對整個測井方案的制訂以及對測井儀器的選用，避免因為方案不合適導致的浪費。

近年來隨著計算機技術的不斷進步，人們通過對已有的數據集進行機器學習，能夠很好的對新的數據進行預測，國內外已經有運用機器學習神經網絡等手段對流體物性參數（PVT）進行處理預測的先例[1]，因而利用機器學習方案處理井下數據，進而對井下流體流型進行預測不失為一種可行的方案。同時通過將傳統測井與機器學習算法相結合，有助于整個測井行業進入智能化、高效化的新發展階段，更加符合新時代下傳統產業數字化轉型，促進新技術在傳統行業中發揮作用。

1.算法原理

(1)BP神經網絡分類算法

其基本原理如下[2,3]：利用多層感知機（Multilayer Perceptron，MLP），根據現有的大量已知數據，將每條數據的特征匯總成數據集X={x1，x2……xn}，每條數據都對應一個標簽y，通過對數據集上訓練來學習函數f(·):Rn→Ro，其中，n為數據集中數據的維數；o為輸出后的維數。和傳統線性回歸不同，在通過MLP進行學習時，輸入層和輸出層之間，會存在一個或多個非線性層，稱為隱藏層，圖1為一個具有兩層隱藏層的MLP。

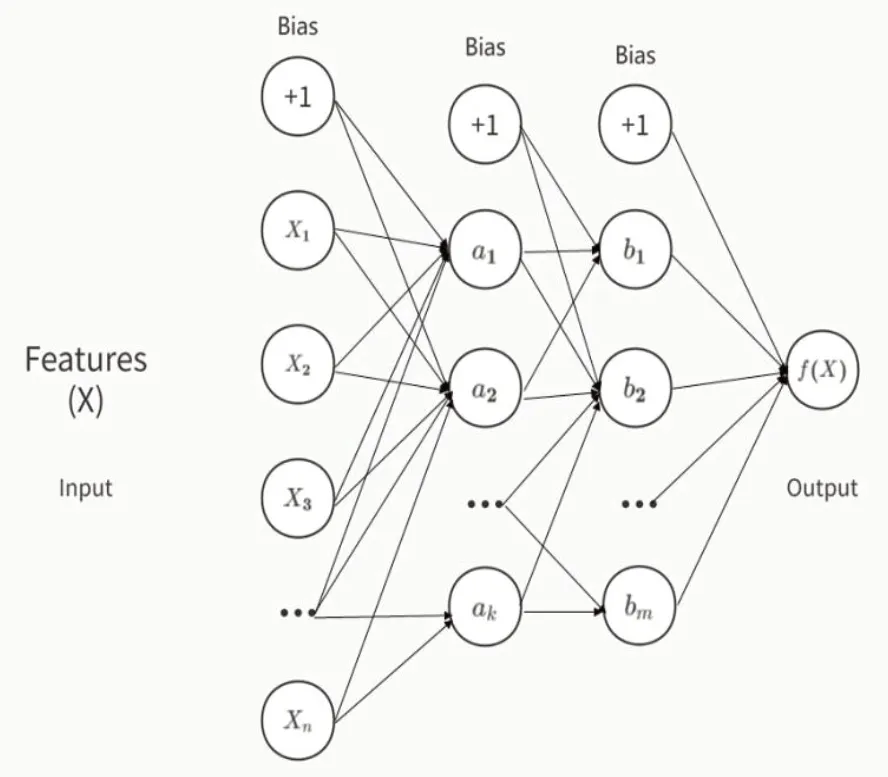
圖1 具有兩層隱藏層的BP神經網絡

最左邊的層叫輸入層，將已有數據標準化后，作為代表輸入特征的神經元；然后經過一層或多層隱藏層中的神經元將前一層的數據加權線性求和轉換w1x1+w2x2+……+wnxn，并通過非線性函數g(·)R→R，g(·)也被稱為激活函數，通常采用：

最后由輸出層接收最后一個隱藏層轉換后的值。

MLP采用了隨機梯度下降（Stochastic Gradient Descent）進行訓練，將需要調整的參數通過使用損失函數進行梯度更新，以獲取更新后的參數：

其中，η為控制參數空間搜索步長的學習速率；Loss為神經網絡的損失函數。

MLP采用均方差損失函數：

在最初的隨機化權重時，多層感知機通過重復更新權重，使得損失的值最小，在計算損失之后，反向傳遞至輸出層的前一層，為每一個權重參數提供一個更新值，從而減少誤差。

隨著梯度下降，計算得到對每一個權重所損失的梯度▽Lossw，并從總損失中減去，即：

由于在對井下流體流型的預測中，井下流體參數并不是唯一的，因而需要解決多個類同時存在的情況，故在隱藏層中學習函數f(x)=W2g(W1Tx+b1)+b2本身為一個n維向量，通過Softmax函數：

其中，zi為Softmax中輸入的第i個元素，其對應與相應的第i類；K是所有類別的總數量，輸出的值包含了樣本中屬于每一個類的概率的向量，最終輸出的結果為概率最高的類。

(2)樹模型分類算法

其基本原理如下[4]：通過創造一個模型，使程序對該模型進行學習，最終從模型數據特征中推斷出的簡單決策規則來預測新的輸入變量的值。

將已有的數據標準化后分條作為訓練向量xi∈Rn，i=1,……,l和類向量y∈Rl，利用決策樹遞歸劃分空間，將相同類別的樣本劃分至同一個組，節點m處的數據集用Q表示，對于一個由特征j和閾值tm組成的階段劃分數據集θ=(j,tm)，將數據分別作為兩個分支：

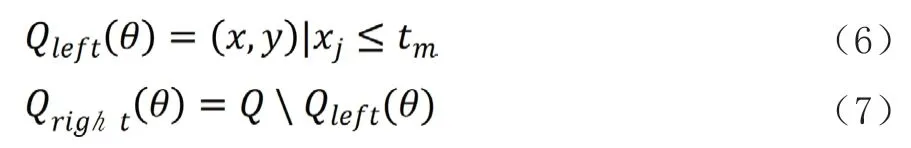
節點處的不存度用不存度函數H(·)計算：

其中，Pmk表示在具有Nm個觀測值的區域Rm中，節點m在k類中所占的比例，故Pmk公式為：

Xm為節點m中所包含的已知數據。

井下流體包含多種流體種類，因而得出的結論也是多種類的，故需要將類向量集定義為一個二維的數組；對每一種輸出的結果需要建立一個估計器，依據每一種類別的輸出平均減少量來作為每一棵分支的產生標準。

2.方法應用

由于實際生產情況具有多種不同井況條件，因而分別采用了在井斜角度0°、60°、85°、90°下，含水率20%、40%、60%、80%、90%，流量100m3/d，300m3/d，600m3/d的實驗數據，各個數據間差異較大，如果直接使用會造成部分數據所占權重過大影響最終結果的情況，因而需要對數據進行標準化處理，采用離差標準化處理，使得所有數據結果值映射到[0,1]區間內，所用函數如下：

其中，xmax為數據中的最大值；xmin為數據中最小值。

然后將標準化處理的數據集中每個數據分別進行加權線性求和，利用損失函數計算損失后反向傳播至前一層以減小誤差，最終達到設定的最大迭代數時結束計算，BP分類算法結束。

再對標準化處理的數據進行評估，選出其中最具有決定性的特征，然后將原始數據集劃分為幾個子集，這些子集分布在第一個決策點的所有分支上，如果一個分支上所有數據都是同一類別，則不需要繼續分類，若包含有不同類別，則需要繼續選出最具有決定性特征來繼續劃分，直至所有葉子節點上的類同屬于一類特征，圖2為決策樹模型運算結果，決策樹算法結束[5]。

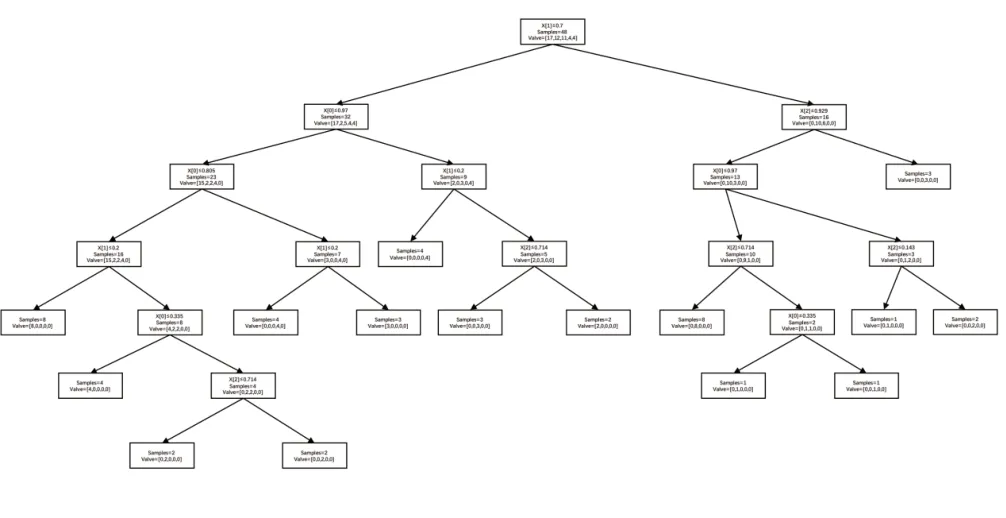
圖2 良好決策節點進行決策分支的決策樹

3.實驗

(1)設計實驗

實驗所用的數據包括實驗數據和實際數據，將實驗數據作為數據集以供機器學習算法學習，然后將實際數據輸入學習后的算法進行預測，將預測后的結果和實際流體流型進行對比，以檢驗算法的可行性。

實驗數據包含井斜角度、流體流量（m3/d）、含水率、溫度、管徑，將實際數據帶入至通過實驗數據訓練學習后的模型，得到對實際數據預測的流體流型，與實際結果進行對照；通過分析不同流量、井斜、含水率下的準確度，判斷算法的可行性。

(2)預測結果分析

在學習算法結束之后，隨機選取不同井斜、含水率、流量的12組已知數據，對數據進行預處理后，然后使用訓練過的神經網絡進行預測，將預測結果與實際數據進行對比，以檢驗BP分類算法和樹模型分類算法對流型預測的準確率。

BP分類算法和樹模型預測結果如表1所示。

表1 BP分類算法與樹模型預測結果

從表1可知，在井斜角度較低時，BP分類算法得到的預測結果較井斜角度較大時的準確度有大幅度提升，在井斜角度較大時預測準確率較低，總的預測準確度在75%左右。而從圖3來看，決策樹模型在決策點選擇較好的情況下，在各流量、各井斜、各含水率上均有較為準確的預測結果，總體準確度能達到90%以上。

圖3 兩種算法與實際流型結果比較

4.結論

將實驗數據分別按照BP分類算法和樹模型算法進行預測后與實際流體流型對比后可以得到如下結論：

（1）通過機器學習BP分類算法和樹模型算法進行井筒流體流型預測，對井下流體流型預測提供了新的解決方案。其中BP分類算法在井斜角度較大的情況下能取得95%以上的準確識別率，但是在其他條件下效果較差；樹模型算法在各種井斜、流量、含水率下均有較為準確的預測，綜合準確度在91.7%左右。

（2）通過較為合適的數據標準化處理，可以降低某些數據在預測中占有過高權重，減少了數據處理后的誤差，提高了數據處理的效率。

（3）通過不斷完善訓練數據集的數據，可以不斷提升預測結果的準確度，為后續該算法在實際應用中打下良好基礎。