基于超循環理論的土地利用結構預測模型與實證研究

王 礫，李貴才，晁 恒

（1.北京大學城市規劃與設計學院，廣東 深圳 518055；2.北京大學城市與環境學院，北京 100871；3. 北京大學（深圳）未來城市實驗室，廣東 深圳 518055；4. 深圳市新城市規劃建筑設計股份有限公司，廣東 深圳 518172）

1 引言

地球表層系統的變化和預測一直是地理學研究的主要內容，相關研究關注各圈層、各要素以及自然和人文現象之間的相互作用關系[1]。國際全球環境變化人文因素計劃（IHDP）與國際地圈生物圈計劃（IGBP）于1995年聯合提出了“土地利用/覆被變化（LUCC）”研究計劃，由此將土地利用變化相關研究推向了自然、人文和地理信息系統等地理學多分支學科的交叉研究領域[2]。之后多學科的推動促使了土地利用/覆被變化研究領域的不斷深入和拓展，該領域研究的重點主要集中在以下4個方面：（1）土地利用/覆被變化的建模與預測；（2）土地覆被變化情況的評估；（3）在不同空間尺度中，土地利用/覆被變化不同驅動力間的關聯；（4）數據信息系統與數據開發活動[3]。

其中，土地利用變化模型作為用于刻畫土地格局變化與動態的重要工具，一直以來都是土地利用和土地覆被變化研究領域的重要內容[4-5]。學者們從多視角，基于不同建模目標，采用多種方法構建了不同類型的土地利用變化模型，如機器學習和統計模型、元胞模型（CA模型）、馬爾科夫模型（Markov模型）、部門經濟學模型、空間分解的經濟學模型、多主體模型等[6]。其中空間模型主要是對土地利用的空間位置變化進行計算，而在計算過程中所需要的速率、數量特征，都是從非空間模型計算中才可以得到的[7]。數量預測模型根據其預測方法原理大體可分為因果型預測方法和趨勢外推預測方法。因果型預測方法主要是參照相關原理進行分析，明確預測對象與影響因素之間所存在的相關性，并基于此進行預測。采用因果型預測方法的典型模型為系統動力學模型（SD模型）等。趨勢外推預測屬于慣性原理的范疇，其借助于研究對象的過去和現在進行對比分析，參照相關信息，對變動情況進行預測，推測以后可能發生的情況。典型的采用趨勢外推方法的模型為灰色系統模型和馬爾科夫模型等。本文所引入的超循環理論也是一類采用趨勢外推方法的數量預測模型。

從具體研究來看，學者們在反復采用空間模型和非空間模型的各種組合，其中CA-Markov 是較為常見的組合方式[8-14]。這兩類模型雖然在實踐中得到了充分應用，但也面臨著長期缺乏理論創新的困境。更具體地，土地利用系統作為典型的復雜系統[15]，現有模型多為局部均衡分析模型，缺乏從系統科學視角來對其進行考察。

本文所引入的超循環模型在一定程度上可以說是馬爾科夫模型的擴展。馬爾科夫模型已經被學者大量使用，且較少對其進行修改。然而馬爾科夫模型中最重要的轉移矩陣來源于一個地區過往的土地利用歷史數據，這些數據不可避免的將產業、人口、規劃等要素被動的加入其中，且無法將其剝離并加以修正。至于想得到一個更具操作性的土地利用結構演變的機制和模型則需要將產業、人口、規劃等要素作為一個外生變量，而不是一個內生變量，這一點馬爾科夫模型是無法做到的，而本文探討的超循環模型則在一定程度上可以做到。

2 超循環理論

原聯邦德國化學及分子生物學家EIGEN于20世紀70年代初在研究生物大分子自組織過程中建立了超循環理論（The Hypercycle Theory），超循環理論和耗散結構理論、協同學一起被稱為20世紀70 年代后出現的三大關于非平衡系統的自組織理論[16]。超循環理論不僅為理解作為“自然規則”的生命及生命起源提供了定量的、規律性的解釋工具，而且由于在社會經濟組織中也存在著超循環組織形式，該理論因而也具有重要的社會科學意義[16]。EIGEN將生物化學中的各種循環分為三個層次：反應循環、催化循環和超循環，由于這一理論的復雜性，本文不對這三個層次的循環進行詳細的闡述，詳細信息可參考EIGEN的著作[17]。在此僅說明第二層次循環即催化循環（記為i）為可區分的一類自復制個體，本文將其與一類土地利用類型進行類比。超循環理論所描述的系統是多種多樣的，其中一類最為典型且簡單的系統被稱為達爾文系統，也即是被定義為滿足以下幾個必要條件的系統：（1）遠離平衡；（2）自復制；（3）突變性。這三點將在下文結合土地利用系統進一步進行闡述。EIGEN將滿足這三個必要條件的達爾文系統用式（1）來描述：

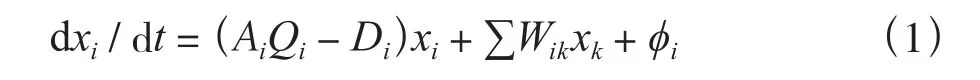
這一微分方程（i為大于1的正整數）被稱為“Eigen進化方程”（也稱之為超循環模型），它描述了系統中各類可區分的自組織個體規模的演化規律。式（1）中下標i表示所有可區分的自復制個體（催化循環）。xi表示相應的群體變量，在生化反應中表示濃度。（AiQi-Di）xi表示個體的“代謝”，Ai是在模板的控制下物質i的復制率（生成率），Qi是模板的品質因子即反應其正確復制i的能力，AiQi表示自發生成的速率，Di表示分解（消亡）速率，而速率是指每單位時間生成或消亡的比例，簡單來說這一項表示了某種個體獨立于其他個體的演化趨勢。個體i的演化并不只取決于自我的獨立規律，它同時也會接受和它相關的其他種類個體的貢獻，這點由∑Wikxk加以考慮。最后一項?i描述了任一種類i的供給或是移走，對這一項的理解可以是多樣化的，可以是系統內在的限制因素，也可以是外界強加的因素，對這一項的不同定義可以描述一個帶有競爭的系統演化過程，諸如總量固定（恒組織）、有限增長和無限制增長的系統，亦可以單針對某一類或是幾類個體加入特定限制以觀察其他種類或是整體規模的演化規律。

3 土地利用系統的超循環特性

從超循環理論的角度來考察土地利用系統，應首先確定土地利用系統為復雜系統，并且通過超循環系統三個必要條件的考察確定其為達爾文系統才可進行。達爾文系統是一類簡單并且典型的超循環系統，如果土地利用系統經考察為一個達爾文系統，則可以采用超循環模型（即Eigen進化方程）進行描述。

3.1 土地利用系統是復雜系統

土地利用系統的復雜性已有大量學者進行了闡述，例如梁勤歐從6個方面總結了土地利用系統的復雜性，即結構層次性、關聯復雜性、不確定性、開放性、動態性和非線性[18]。在采用復雜科學理論研究方面亦有大量學者對土地利用系統進行了闡述，例如信息論與分形理論的應用[19]、自組織理論的應用[20]、混沌理論的應用[21]等。這些闡述都證明了土地利用系統是一個典型的復雜系統。

3.2 土地利用系統滿足達爾文系統的必要條件

將不同用地類型類比為超循環系統中可區分的自復制個體（i），可區分的自復制個體濃度xi則類比為土地利用系統中土地利用類型的面積，AiQi表示一類土地利用類型的自發增長速率，Di表示一類土地利用類型消亡（轉化為未利用地）的速率，Wik表示其他土地利用類型轉化xi的速率，?i則代表內在或是外在的限制條件，之后將在與馬爾科夫模型類比時進行進一步闡述。逐條考察土地利用系統是否滿足上述達爾文系統的三個必要條件，即遠離平衡、自復制與突變性。由于遠離平衡是所有復雜系統都具備的屬性，平衡態所要求的微觀可逆性不可能帶來復雜性，因此本文僅對土地利用系統的自復制性和突變性加以闡述。

3.2.1 土地利用系統的自復制性

自復制性指競爭系統中的某些組分存在內在的機制或能力以使得自身數量增加，這一屬性包括兩個核心要素，即競爭與組分增長。在土地利用系統中由于城市化和集聚效應等原因，這一系統作為整體或是組分都存在增長的趨勢，同時土地面積的有限性，尤其是城市土地的有限性又不可避免的導致了各用地類型間的競爭。通過前述對Eigen進化方程的闡述可以明顯發現，自復制性并非要求系統中每一種組分都必須有著正的（AiQi-Di）xi+∑Wikxk項。這兩項之和為負也并不影響這一動力學模型，保證各組分產生競爭即可，可見土地利用系統滿足自復制性。

具體來看，以一類土地利用類型為系統的組成部分，采用“復制”這一角度進行分析的方法大體上可以分為兩類：一類是空間的；另一類是非空間的（即不考慮空間要素的）。在非空間中采用“復制”思維的典型方法是馬爾科夫模型，在空間方法中采取“復制”思維的典型方法是元胞自動機（CA）。元胞狀態可以是{0，1}的二進制形式，嚴格來說元胞自動機的元胞僅能夠存在一個狀態變量。但是需注意的是，在實際應用階段一般都會對元胞執行擴展操作，在此背景下每個元胞便能夠擁有多個狀態變量。例如，李才偉根據實際情況設計了“多元隨機元胞自動機”模型，并對元胞空間的鄰域關系進行了定義，使得各個元胞在空間內都擁有有限個鄰域[22]。根據不同的鄰域規則，鄰域的空間在一輪之后有一定的概率復制原空間的屬性，同樣也有一定概率復制錯誤，從理論上講這也是“突變”產生的緣起。

3.2.2 土地利用系統的突變性

突變性這一必要條件是指某種組分在復制過程中發生錯誤進而產生新的組分。由于超循環理論誕生于大分子演化研究，一個分子在演化之初可能只有一種自復制組分，復制的突變性保證了新組分的出現，從而保證了競爭與系統演化的產生。而土地利用系統同樣滿足突變性這一條件，即某一塊土地的所有者出于某種原因變更了土地的使用類型，這可以被視為土地利用類型意義上的突變。即使從理想城市模型研究的角度上看，將最初的城市設定為單一類型的土地利用（雖然此時不應稱其為“城市”），在其自身擴張的過程中某一塊土地的所有者出于某種原因變更了土地的使用類型從而產生了新的組分，也就開啟了不同組分在面積有限情況下的競爭。因而，這一超循環理論角度的理想城市模型亦是合理的。在土地利用變化數量結構研究領域被廣泛應用的馬爾科夫模型也已經蘊含了這一突變的思想，而在空間研究方面，突變也是元胞自動機視角下土地利用變化中的重要組成部分。

綜上，土地利用系統是一類典型的復雜系統，且滿足達爾文系統的三個必要條件，即遠離平衡、自復制與突變性。也就是說土地利用系統是一個達爾文系統，進而可以采用超循環模型（即Eigen進化方程）分析土地利用系統的演化規律。

4 土地利用結構預測的超循環模型

4.1 馬爾科夫模型與超循環模型的比較

馬爾科夫模型是預測土地利用數量結構變化最常用的模型之一（式（2）），馬爾科夫模型通過計算某一類土地利用在單位時間內轉變為另幾類的概率，將土地利用結構的演化過程看作各土地利用類型（包括未利用地）以一定的概率相互轉化的過程，在具體操作中將土地利用變化看作是初始矩陣與概率轉移矩陣進行反復相乘的過程。具體來看，即將任意一類土地利用類型的面積表示為xi，任意時期tn到下一時期tn+1，xi的變化量可以表示為兩部分的和，也就是自身轉化為自身的部分再加上除自己外其他用地類型轉化為xi的部分。通常在實際研究中采用的馬爾科夫模型的步長為若干年，不過使用土地利用結構平衡表可以得到年均轉移情況[23]。

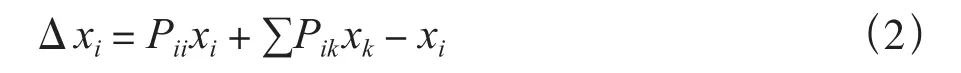
反觀超循環模型（式（1））可以發現，將本作為一類土地利用類型面積的變量xi考慮為這一組分占全部的百分比，參數Wik的含義不變，對應式（2）中的Pik，即組分xk（百分比）轉化為xi（百分比）的概率，即：

則與馬爾科夫模型相比，僅憑∑Wikxk項還缺少ii的面積（概率）乘以轉移為自身類型的概率Pii這一部分，微分方程組中（式（1））的AiQi-Di項是一個常數，如果令AiQi-Di=Cii- 1 ，則超循環模型的形式則變化為：

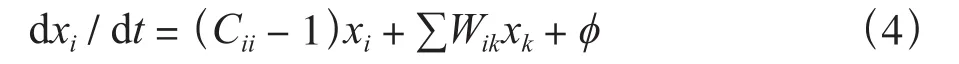
該模型（式（4））與馬爾科夫模型（式（2））相比，僅僅多出一個常數項?，如果再令?取0的話，并令∑Wik= 1（i為1，2，…，n中的任一值），超循環模型則完全退化為馬爾科夫模型，即Cii事實上就是馬爾科夫模型中的Pii，也就是說馬爾科夫模型是超循環模型的一個特例。從理論上講，如果說馬爾科夫模型在土地利用變化方面的應用是成功的，那么將超循環模型應用于土地利用演化方面的研究也必然是可行的，并且是存在一定優勢的。

4.2 超循環模型的參數計算

超循環模型認為系統中每一種組成成分的變化機制都是相同的，也就是說方程組中每一個方程的形式都是相同的。每一個微分方程都擁有數量相同的若干個參數，假設一共存在n種組分，則超循環模型（式（1））中含有參數Ai、Qi、Di、Wik和?i，其中在每一個微分方程中Wik的個數為n- 1個（這些參數不排除為0），那么一個微分方程中的參數就有n+ 3個，一共有n個微分方程，那么整個微分方程組就有n（n+ 3）個參數。由于數據量很難滿足要求，如果采用計算機數學軟件對微分方程組進行參數擬合則難以實現。也就是說當有足夠的數據量時理論上可以通過數學軟件進行參數擬合來確定未知參數。

如果沒有足夠的數據直接進行參數擬合，那么微分方程組的參數只能通過其他方式獲得，上文對于超循環模型與馬爾科夫模型進行了較為詳細的對比分析，并認為馬爾科夫鏈模型是超循環模型的一個特例。對比分析結果暗示了除了直接采用數學軟件進行參數擬合之外，還存在另一種簡略估計未知參數的方法。根據超循環模型與馬爾科夫模型的異同點，馬爾科夫模型與超循環模型同樣將系統演化的過程看作是不同組分相互轉變的過程，只不過馬爾科夫模型將不同組分之間的相互轉化作為系統變化的全部機制，而超循環模型將此作為系統變化的一部分機制。因此，超循環模型表示不同組分之間的相互轉化的項（即因其他組成成分自身復制的不精確性導致的項∑Wikxk）是獨立存在的（僅與代表復制準確率的參數Qi存在守恒關系），也就是說可以用其他方法將參數Wik單獨計算出來，而馬爾科夫模型中計算轉移矩陣（式（5））的方法即為最佳選擇。

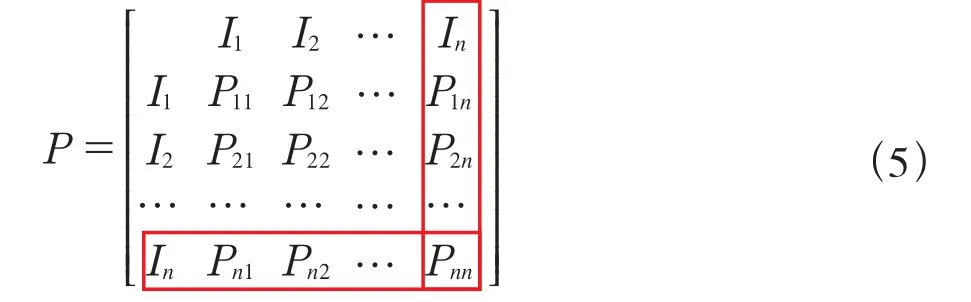
假設In代表的土地利用類型為未利用地，由于超循環模型可不考慮未利用地這一類型，其他任一用地類型轉化為未利用地，超循環模型將其視為“消亡”，所以這一馬爾科夫轉移矩陣最后一列與最后一行不考慮。超循環模型中的自身增長不能簡單對應于馬爾科夫模型中自己以一定概率“轉化”為自己，因此不考慮轉移矩陣中主對角線上的數值，即式（6）。

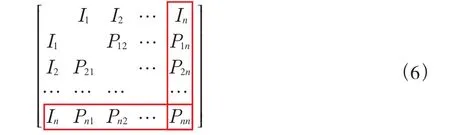
其中任一去除最后一行、最后一列和主對角線上的數值后，剩下的部分則完全對應于超循環模型（式（1））中的第二項，即Pij=Wik。這樣一來就極大的減少了超循環理論模型中參數的計算量。每一個方程中只剩下如下幾個參數需要確定：Ai、Qi、Di和?i。首先，Dixi是指一類組分xi的自身消亡（分解），Di是消亡（分解）速率，通過觀察狀態轉移矩陣，這一參數正好對應于除未利用地之外的任一用地類型轉化為未利用地的概率Pin，即Di=Pin。至此每個方程中還存在3個參數距要計算，即：Ai、Qi和?i。

Ai和Qi在模型中以相乘的形式存在，在計算時完全可以認為是一個參數，如果得知二者的乘積，是存在辦法可以將二者分離的。由于第二項所表示的不同組分之間的相互轉化，這一項的來源是由于各個組分復制的不準確性，也就是說Qi與Wik存在一個守恒關系，即：

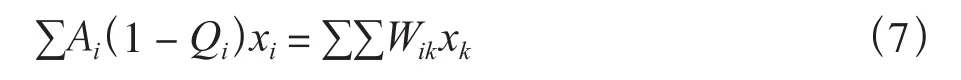
通過這一守恒關系可以將Qi計算出來。至此，還存在兩個參數需要計算，即AiQi（可認為是一個參數）和?i。這兩個參數從轉移矩陣中無法簡單得出，但通過剛才的分析已經極大的減少了需要確定的參數數量，每一個公式最多有兩個（?i可以選擇非專一形式時則只有一個），這樣一來再運用數學軟件進行微分方程組的參數擬合就是可行的。對于Eigen進化方程的最后一項?i，本文將其定義為這樣一個形式，所有土地利用類型中的約束值都與它們的實際面積xi成比例：?i=?xi/c，c=∑xi。這一形式有如下3個優點：（1）所有xi共享數值相同的一個參數，便于計算；（2）對于某一類所占比例較大的xi，?i將對其產生明顯的抑制作用；（3）通過演化系統規模可以滿足條件dc/dt= 0，此時限制條件?正好調節到抵消了凈的超額增長。

5 實證研究

5.1 研究區域與數據來源

本文選取深圳市作為實證區域。深圳市土地總面積1 997.27 km2，下轄福田區、羅湖區、南山區、鹽田區、寶安區、龍崗區、坪山區、龍華區、光明區9個行政區和大鵬新區。深圳市土地利用變更調查自1990年開始，至今每年都對調查結果進行更新。本文采用1990—2011年深圳市土地變更數據進行參數計算與擬合。土地利用變更調查分類采用中華人民共和國國家標準《土地利用現狀分類》（GB/T 21010—2007）。由此，在本文中深圳市土地利用變更調查的土地利用類型的一級類將分為8類，即耕地、園地、林地、牧草地、居民點及工礦用地、交通用地、水域及水利設施用地和未利用地。根據前文所述，超循環模型雖然可以不關注未利用地，但在實際計算中，由于需要借助馬爾科夫模型進行相關參數計算，因此在相關參數計算過程中，需要將未利用地納入進來。

5.2 參數計算

首先，采用馬爾科夫模型計算超循環模型中的參數值。在土地利用規模預測研究中，獲得轉移矩陣可以通過一定時間跨度的同一地區各類土地利用的面積和空間數據利用ArcGIS軟件計算得到土地利用變化平衡表，再采用此表計算得到土地利用結構平均轉移概率矩陣。圖1為深圳市2000年和2009年的土地利用現狀圖，表1為深圳市2000年和2009年各類用地面積和比例。

圖1 深圳2000年和2009年土地利用現狀圖Fig.1 Land use status map of Shenzhen City in 2000 and 2009

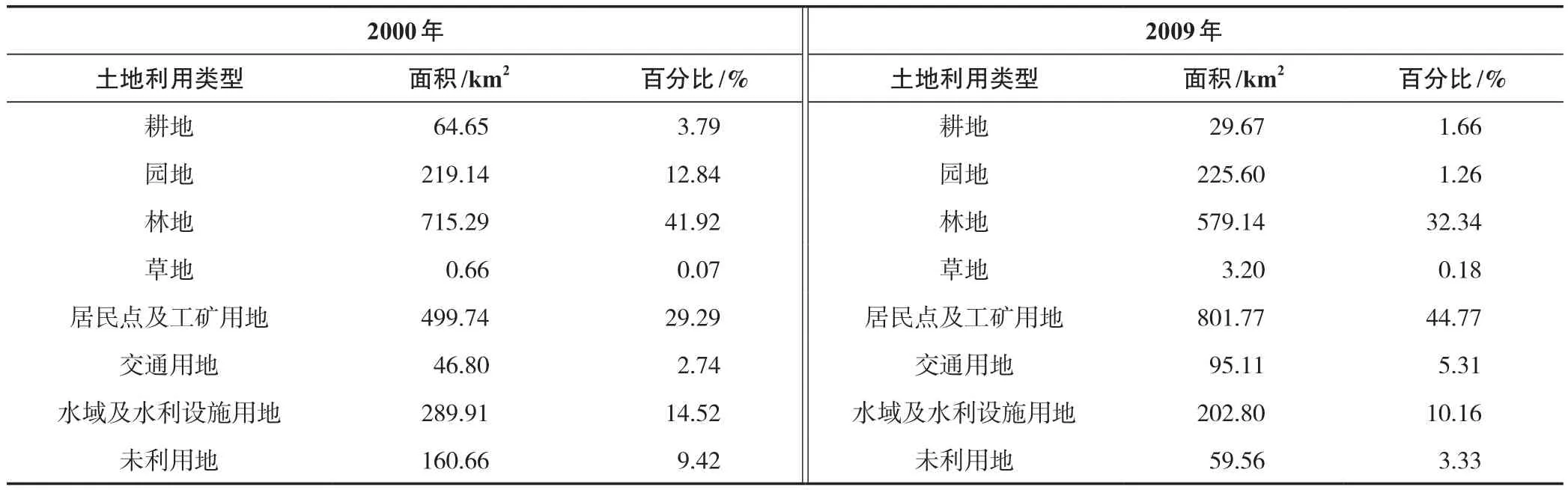
表1 2000年和2009年深圳市各類用地面積和比例Tab.1 Area and proportion of various types of land in Shenzhen City in 2000 and 2009

以深圳市2000年和2009年的土地利用變更調查數據為基礎，采用ArcGIS union工具計算深圳市2000—2009年各類用地之間相互轉化的數量（即土地利用平均變化平衡表），計算結果如表2所示。

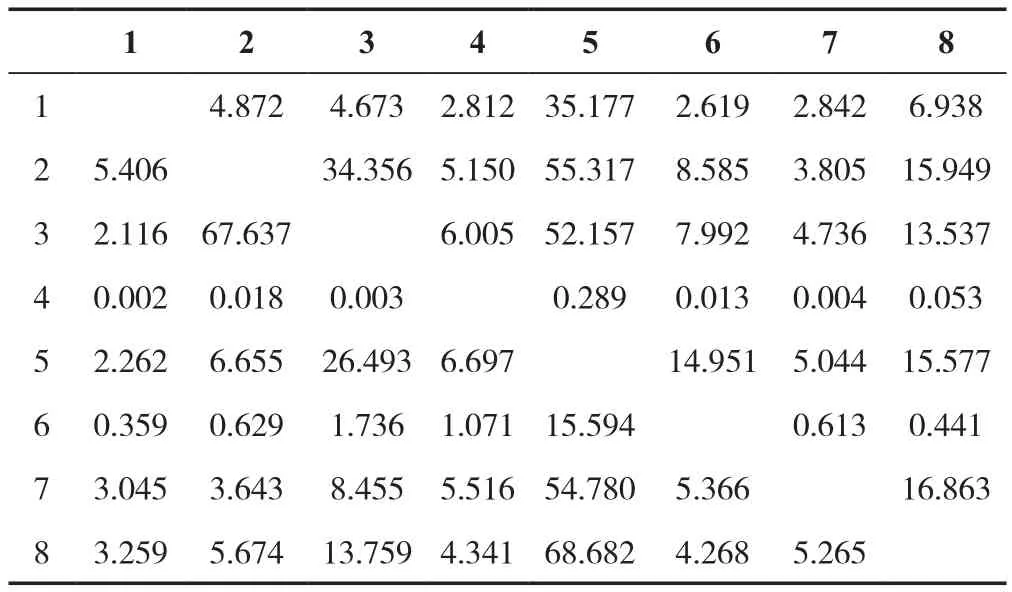
表2 2000—2009年各類土地利用類型轉移面積Tab.2 Transfer area of various land use types from 2000 to 2009 （km2）

由此可以得到各類土地利用類型平均轉移面積，以此計算得出這期間全市土地利用結構得平均轉移概率矩陣表3。其中，前7列轉移概率矩陣即為超循環模型方程組中的Wik值，最后一列元素則對應于Di。

表3 深圳市各類土地利用類型年均轉移概率矩陣Tab.3 Annual average transfer probability matrix of various land use types in Shenzhen City

為方便計算，令式（1）中AiQi=Fi，則有：

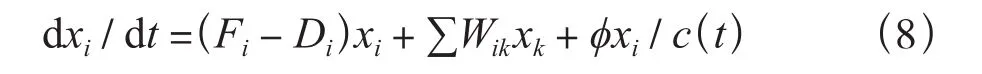
通過上文的計算，Di、Wik為已知值，然后求解Fi和?。使用開放式計算軟件OpenLu，采用1990年至2011年深圳土地變更調查數據進行擬合計算。經多次計算可得：F1=0.000 554 752；F2=0.000 755 215；F3=0.000 821 480；F4=0.000 635 266；F5=0.003 387 175；F6=0.001 874 625；F7=0.000 004 174；?=-55.440 280 229 159 6。至此，超循環模型中所有參數都已計算出，模型具體形式見表4。

表4 超循環模型的具體形式Tab.4 Specific forms of hypercycle model

5.3 實證結果分析

根據此方程組及參數值，以2013年深圳市各類土地利用面積為基期數據，分別采用馬爾科夫模型和超循環模型方程組預測深圳市2018年各類土地利用面積，并將兩種預測值與深圳市2018年各類土地利用現狀值進行比較（表5）。

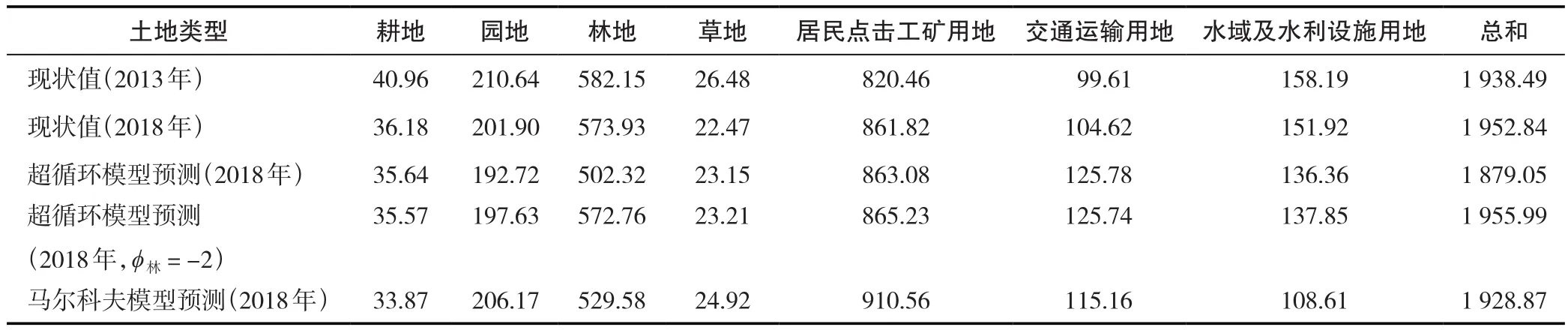
表5 2018年深圳市各類土地利用面積現狀值和預測值Tab.5 Status quo and predicted results of land use area in Shenzhen City in 2018 （km2）

從實證結果來看，在耕地、園地、草地居民點及工礦用地和水域及水利設施用地方面，超循環模型均比馬科夫模型更加貼近實測值。以居民點及工礦用地的預測為例，2018年現狀值為861.82 km2，超循環模型預測為863.08 km2，僅相差1.26 km2，而馬爾科夫模型預測為910.56 km2，相差為48.74 km2。顯然，馬爾科夫模型高估了居民點及工礦用地的增長趨勢，而超循環模型預測值較為準確。從模型原理來看，超循環的動力學模型（式（8））最后一項?xi/c（t）對其增長產生了明顯的遏制作用。

然而，在林地和交通運輸用地方面馬爾科夫模型預測卻相對更加準確。究其原因如下：（1）超循環的動力學模型（式（8））最后一項?xi/（ct）的?值為了簡單處理對所有用地類型都取了同一個值，而深圳市林地面積所占比重較高，使得這一項數值也較大，這也就嚴重低估了林地的面積。然而，現實中林地是一類比較特殊的用地，由于自然條件以及政策的限制等原因使得這類用地并不會大面積的減少。對于這類問題，超循環理論的模型可以通過對其設立一個獨有的、非共享的?值予以解決。（2）對于交通用地的預測，超循環模型對于這類用地的預測值也不如馬爾科夫模型準確，其高估了交通的擴張速度，這一現象的產生也是由于交通用地的特殊性導致的。在城市建設用地快速擴張的階段，交通用地也是隨著這一趨勢快速增長的，但是城市發展到一定水平，已有的交通基礎設施足以滿足對于交通的需求時，交通用地面積的變化將趨于減緩。這一機制在超循環理論中沒能被描述出來，以至產生這樣的偏差。對于這一問題的解決，也類似于對于林地的處理方法，在交通基礎設施完善之后，對交通用地設立一個獨有的、非共享的?值以抑制其增長。

2005年深圳在全國率先劃定了974.5 km2的基本生態控制線，并出臺《深圳市基本生態控制線管理規定》（以下簡稱《規定》）。2005年后基本生態控制線之內的山體、森林、水體得到了很大程度的保護，《規定》的頒布使得深圳市林地、園地和耕地面積自2005年后減少速度明顯減緩，尤其是林地，2006年林地面積為582.03 km2，到了2016年林地面積為578.73 km2，10年僅僅減少了3.3 km2。正是由于《規定》這一政策的頒布以及林地本身的特殊性，在一定程度上產生了上文所述超循環模型在林地面積預測上的偏差。因而，需要給林地獨有的、非共享的?林值，以體現這一政策和其本身的特殊性對于深圳土地利用尤其是林地所產生的影響，也即是選擇的?林值在一定程度上限制林地面積的變化，僅允許有較少量的減少。經過多次測試，發現當?林= -2時，可以滿足深圳市生態控制線的要求，林地的減少得到了很大程度上的控制，同時也符合小幅減少的趨勢。對于超循環模型預測偏差較大的交通用地，由于缺少類似于《規定》這樣硬性的政策限制，為了研究的客觀性則不通過測試的方法獲得其非共享的?值。

可見，由于超循環模型可以通過改變參數?值以表示外生因素的影響，從而使得模型的預測更加接近現實情況，預測結果也更加準確。以2013年作為基年，采用?林= -2時的超循環模型形式對各類用地及總規模在基年之后50年的變化趨勢進行預測（圖2）。從長期趨勢來看，耕地、園地、草地和水域及水利設施用地從比例上講都有明顯減少的趨勢，但這一趨勢都存在著不同程度的減緩。以園地為例，首次迭代時從2013—2014年減少3.44 km2，到了最后一次迭代2063—2064年只減少了不到1 km2。林地通過上文對其變化參數的修正以代表生態控制線的約束，長期變化趨勢一直較為穩定，在長達50次的迭代后僅僅減少了17.9 km2。迭代到2063年各類用地總面積為1 995.28 km2，比上一年各類用地總規模僅增長0.27 km2，并且這一增加值在逐年降低，這是上文對于超循環模型闡述中已經預料到的。值得注意的是，超循環模型除了計算轉移矩陣時曾考慮到了未利用地，而在其他所有參數中都沒有考慮未利用地的情況，也就是說在很大程度上這一模型并不知道深圳市總面積，但是采用它進行預測時所得到最終總規模所收斂的值是和深圳市總面積非常接近的，從圖2中可以明顯看到各類用地總規模將收斂到2 000 km2左右，而深圳市總面積為1 996.85 km2，這也從側面驗證了超循環模型的準確性。

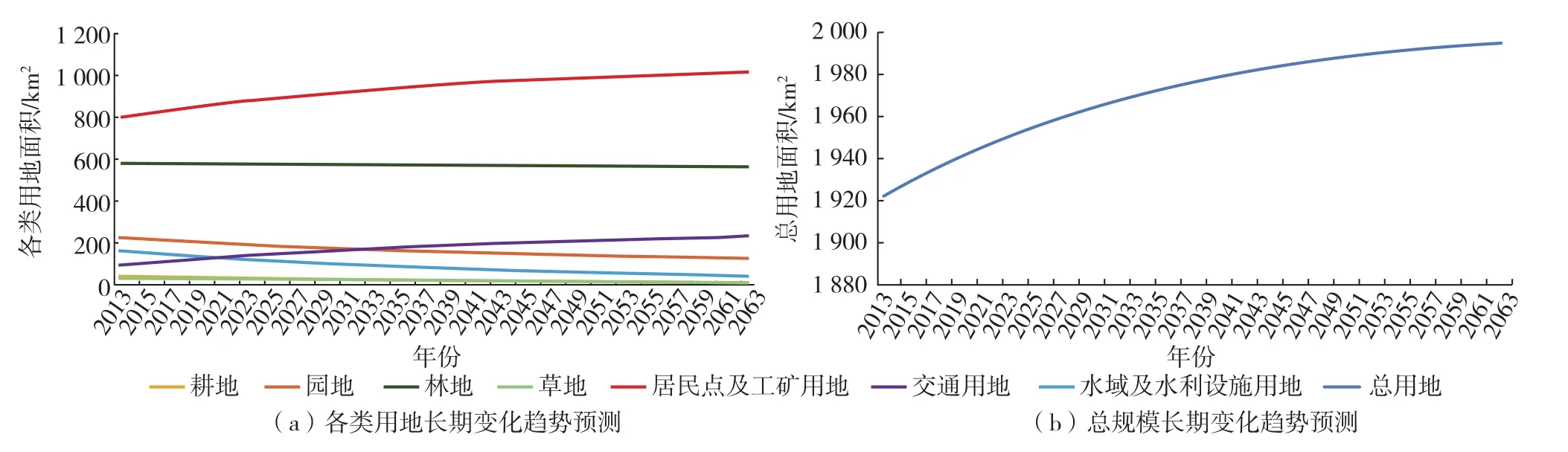
圖2 各類用地與總規模長期變化趨勢預測Fig.2 Forecast of long-term trend of various land use and total scale

6 結論和展望

土地利用變化模型是研究土地利用/覆被變化的重要手段，基于不同研究目標的多學科方法已在土地利用變化模型中得到應用。其中，既有基于歷史土地數據進行外推性預測的結果導向法，又有以分析人地相互作用機制為目的刻畫土地決策的過程導向法。并且，這些模型正經歷從單一的非空間模型向非空間模型和空間模型融合的演進過程。然而，現有模型也面臨著長期缺乏理論創新的困境，土地利用系統作為典型的復雜系統，缺乏系統科學視角的分析。基于此，本文將生物化學及生物物理學交叉理論，即超循環理論引入土地利用變化模型研究中。在對超循環理論剖析的基礎上，建構了用于土地利用結構預測的超循環模型，并以深圳市為例開展了實證檢驗。研究結論如下：

（1）基于超循環系統的演化機制，達爾文系統是一類最為典型的超循環系統，而土地利用系統是典型的達爾文系統，符合超循環模型描述的演化機制。

（2）馬爾科夫模型可以認為是超循環理論中的Eigen進化方程的特例，并以此在理論上論證了超循環理論在土地利用演化研究領域應用的合理性。通過與馬爾科夫模型的對比分析，得到了在數據量不足的情況下對超循環模型中參數的計算方法，并在理論上對超循環理論在土地利用演化研究方面應用的可行性進行了論證。

（3）以深圳市為例，開展了運用超循環模型進行土地利用結構預測的實證分析。實證研究以2013年作為基年，應用超循環模型預測了深圳市2018年的土地利用結構和數量，并將超循環模型的預測結果與土地利用現狀數據和采用馬爾科夫模型預測的結果進行了對比。對比發現，在大部分土地利用類型預測中超循環模型比之馬科夫模型更加貼近現實。對于預測不準確且偏差較大的情況進行了分析，并進一步修正了參數。采用修正過的模型以2013年為基期進行了50次迭代，對深圳土地利用結構進行了長期預測。

本文雖然論證了超循環模型在城市尺度上用于土地利用結構預測的可行性，但并未涉及這一模型在城市尺度之外還存在怎樣的適用性。從這一視角出發，對于超循環模型在土地利用變化領域的適用性尺度應是未來研究的重點方向之一。