基于三次樣條插值BP神經網絡的航空阻力傘供應決策模型

谷雨軒，徐常凱，肖凱銳

（空軍勤務學院航材四站系，江蘇 徐州 221000）

作戰訓練保障任務日趨多元，阻力傘保障作為外場保障的重要一環，必須適應形勢和任務的發展變化，變革保障方式，履行好使命任務。在實際保障中，供應方案通常需要依靠經驗確定，而經驗決策存在不可復制性，有的單位為了滿足任務需要，存在用數量掩蓋決策問題的情況，因此建立阻力傘供應數量模型對于打牢保障效益基礎具有重要意義。

由于阻力傘保障中傘具的消耗數據及對應的任務數據積累較少、獲取困難，且影響因素多，不同條件下的傘具使用規律不盡相同。目前常用的預測方法有滑指數法[1]、BP神經網絡[2]、Bayesian方法[3]等，這些方法對于解決裝備需求預測具備一定的優勢，但在使用的時候局限性也十分明顯。因此為了解決樣本數量少的問題，本文采用三次樣條插值的方法擴充數據，建立BP神經網絡對供應數量進行預測。

1 航空阻力傘供應現狀

1.1 供應方案長期依靠人工經驗確定

隨著信息化建設不斷推進，雖然已經給救生裝具室配備了管理信息系統，但是在實際保障中并沒有得到較好的應用。供應方案一般由救生裝具室主任根據飛行任務和自身保障經驗確定，但是近年來專業人員改行現象較為普遍，根據抽檢情況看，不在位或非救生專業的干部占大多數，在保障任務重的情況下，決策難以保證準確性。

1.2 供應數量影響因素眾多，缺乏規律性

通常情況部分傘具在回收之后可以現場包裝并在此裝機使用，此種情況可以減少攜帶的傘具數量，因此供應方案一定程度上也受到保障人員的包裝能力和工作強度的影響。

1.3 為了滿足任務需求忽視保障效率

一項保障活動通常從軍事性、經濟性、保障性來衡量[4]。在實際工作中，軍事性是部隊保障考慮的首要因素，即滿足首先考慮任務需要。對于阻力傘保障，保障人員常常供應多于實際任務需求的傘具，許多阻力傘并沒有被使用便收回救生裝具室，由于保障人員人數有限，這就增加了運輸負擔，也對使用情況等統計造成了一定壓力。

2 基于三次樣條插值的樣本擴充

2.1 數據準備

為了體現模型的實用性，輸入的參數盡可能少，通過德爾菲法征求專家意見，在眾多影響因素中選擇關鍵因素，最終確定起落架次、工作總時長（即外場包裝總時長）、任務飛機數、傘具的平均剩余使用壽命作為輸入影響因素，其中由于每次起落都會實施拋傘，因此起落架次為確定供應數量最關鍵的因素。

現有某型飛機8個工作日的起落架次、工作總時長、任務飛機數、平均剩余使用壽命和實際準備數量，如表1所示。

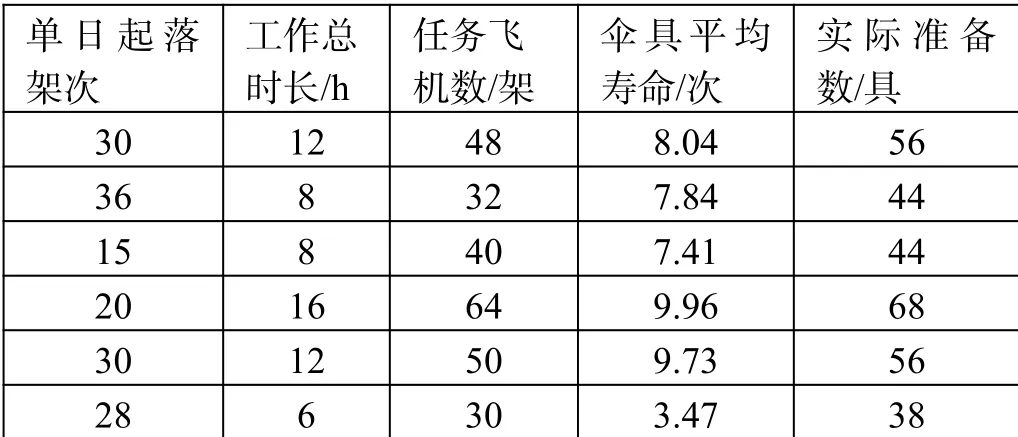
表1 樣本收集

表1（續）

三次樣條插值法原理是在數據節點之間構建3次多項式并拼接成光滑曲線。不難看出在原始數據起落架次中，起落架次為20和30的數據不止一條，因此對重復數據做取均值處理得到三次樣條插值的輸入數據。

2.2 數據預處理

由于樣本數值限制，當起落架次為60時出現異常值負值，在建立神經網絡模型時將此條數據去除。考慮阻力傘由于非保障因素損壞的余度，將飛機數進行向上取整，工作總時長也向上取整，最終在原始數據的基礎上擴充得到起落架次在區間[30，60]之間步長為2的數據，如表2所示。

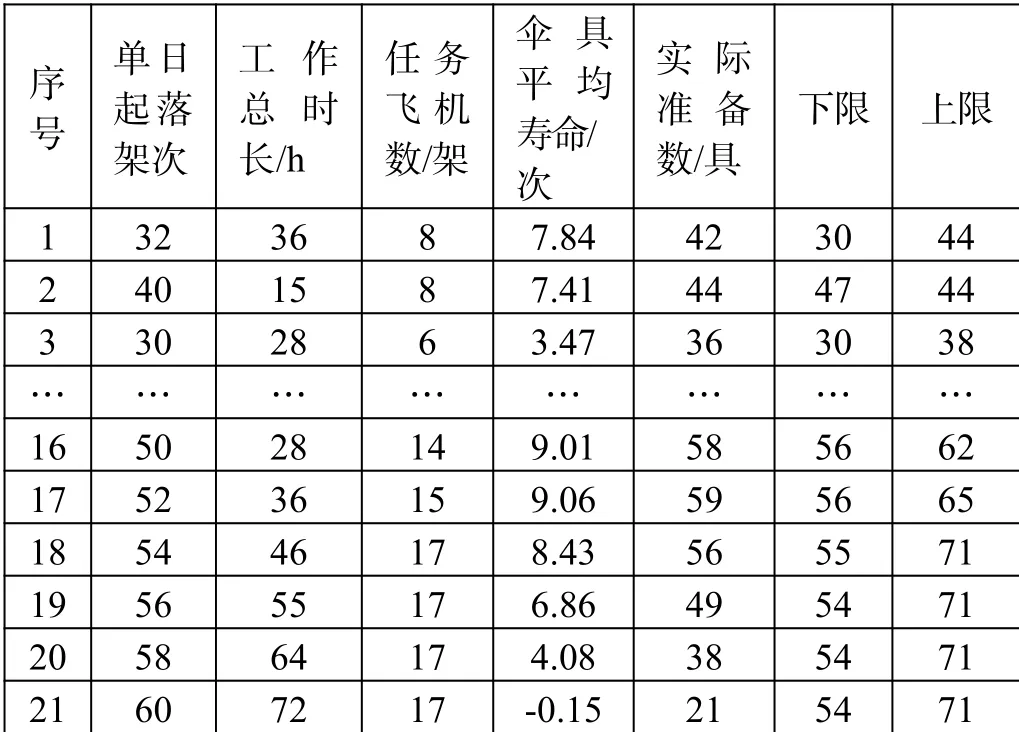
表2 三次樣條插值擴充結果

受到原始數據本身閾值的限制，模型在閾值外的結果誤差較大，有經驗公式用以確定供應方案上下限，經驗公式結果只能作為參考（供應數量上限對于任務飛機數小的情況不適用、供應數量下限對于工作時間較長的情況不適用，且上下限也不是絕對的，存在下限超過上限的可能），公式為：

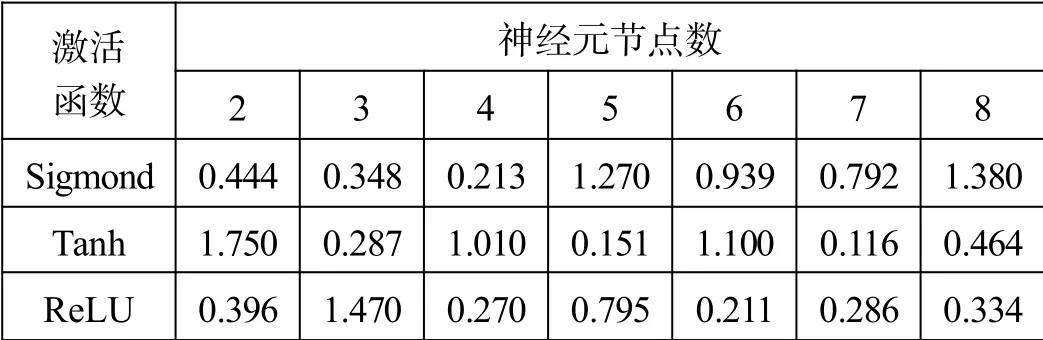
表3 不同神經元節點結果

因此，對于表2中序號19—21的數據視為無效數據去除，將數據1—18作為BP神經網絡模型的基本數據。

3 基于BP神經網絡的阻力傘供應數量模型

BP神經網絡是目前應用最廣泛的神經網絡模型之一，通過誤差逆傳播算法訓練對網絡進行優化，實現對數據的精確擬合[5]。為了消除綱量采用極大極小值歸一化處理。為了消除綱量，對極大極小值進行歸一化處理，歸一化方法為

3.1 模型優化

在建立訓練模型時，需要設置隱藏層節點數即神經元的節點數。若節點數太少，則網絡訓練效果較差；若節點數太多，則會延長網絡訓練時間。因此，找到合適的神經元節點數對于提升模型精度具有重要意義。

將實際準備數取2/3數據作為訓練集，1/3作為驗證集建立BP神經網絡模型。神經元節點數在2～8之間，激活函數分別選擇3種常見的非線性函數，即Sigmoid函數、Tanh函數、ReLU函數重復試驗，根據模型表現的均方誤差（MSE）得到結果，如表3所示。

3.2 模型精度對比

為了得到最優模型，選取3種激活函數中均方誤差表現最好時的神經元個數搭配該激活函數得到3個模型。最終預測值和實際值如表4所示，對比如圖1所示。

表4 模型預測值和真實值

為了對比模型的準確性，比較3種模型預測值和真實值的平均絕對百分比誤差（MAPE）和均方根誤差（RMSE），結果如表5所示。

通過模型精度對比，選擇Sigmond函數作為阻力傘供應數量BP神經網絡模型的激活函數，神經元節點設置為4，此時模型精度最優。

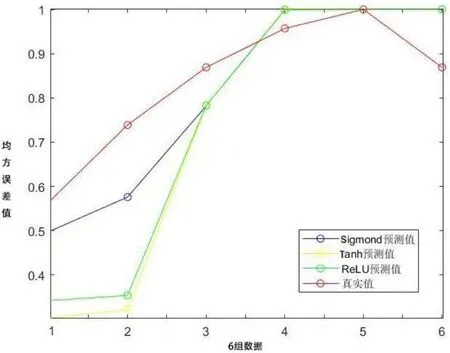
圖1 模型預測值和真實值

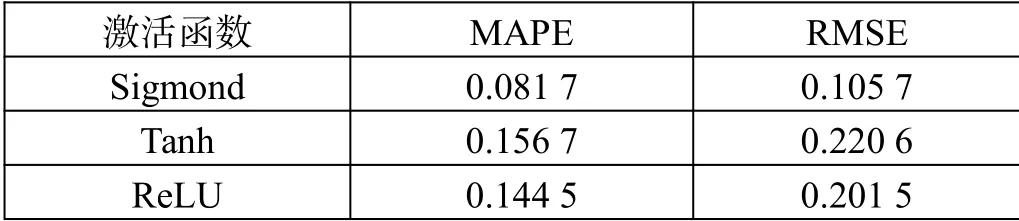
表5 模型精度對比

4 結語

面對當前阻力傘供應方案決策模式與保障要求不適應的問題，本文提出一種基于三次樣條插值BP神經網絡的阻力傘供應數量模型，解決了樣本數據量少、神經元數量確定、神經網絡激活函數選擇的問題，通過模型精度驗證檢驗模型的可靠性。

由于模型初始樣本數量和閾值的限制，三次樣條插值結果會受到影響，在閾值外的插值數據偏離實際，因此需要進行去除處理。其次，擴充后的數據量并不大，對于BP神經網絡訓練模型精度有影響。