基于模型補償的機械臂位置跟蹤控制研究

鐘 輝，袁邦頤，，丁度坤，3，辛曼玉，鄧建新，黃秋林，

（1.廣東匯興精工智造股份有限公司，廣東 東莞523819;2.廣西大學 廣西制造系統與先進制造技術重點實驗室，廣西 南寧 530003；3.東莞職業技術學院 電子信息學院，廣東 東莞 523808）

0 引言

當前機器人在各行各業中均大放異彩，在工業生產過程中，為了在整個過程中實現不同任務下的高效率自動化生產，不同自由度的機械臂在不同生產場景下均有其應用。二關節機械臂以其結構簡單、成本低廉、控制方便等優點被廣泛用于搬運、抓取等作業中[1]，在第二桿后增加一個旋轉和平移關節后就形成了常見的Scara機器人，可實現抓取、分揀等功能，如圖1所示。

圖1 分揀機器人

隨著工作任務需求的不斷提高，如精密裝配、打磨加工等場景，對機器人位置和路徑跟蹤精度要求也越來越高。控制器的跟蹤性能是影響機械臂位置跟蹤精度的主要因素，所以，如何設計一個反應迅速和跟蹤精確的控制器顯得尤為重要。文獻[2]針對二連桿機械臂的運動控制問題提出了一種基于深度強化學習的控制方法。文獻[3]針對用于三自由度機械臂各關節末端軌跡跟蹤控制的非線性系統在擾動存在的情況下跟蹤效率較低的問題，提出一種變增益迭代學習控制律。文獻[4]提出了一種自適應模糊滑模控制算法。采用自適應單輸入單輸出模糊系統來計算控制增益。雖然以上方法對不確定模型下的機械臂位置跟蹤有較好的效果，但均存在收斂慢、跟蹤性能較一般的問題。本研究意在針對模型已知的情況下設計一種控制器，使機械臂能快速準確地跟蹤目標軌跡。

1 機械臂控制方法

1.1 PID控制

1936年Callender和Stevenson等給出了比例積分微分（Proportion Integration Differentiation，PID）調節器的算法。此后不斷有新的控制算法誕生，但仍無法撼動PID算法在控制領域的地位。當前其已經應用于90%～95%的控制電路中，它具有簡單、實用、魯棒性強等優點[5-7]。在實際應用中，一個簡單的線性解耦的PID反饋控制器可以在不引起任何穩態誤差的情況下得到期望的位置。

基本的連續PID控制公式如下[6]：

其中Kp為比例系數，Ti為積分時間常數，Td為微分時間常數，e（t）為目標值宇實際值的偏差，t為時間。

其傳遞函數為：

對于PID策略，用戶也可取消部分環節如（積分或微分環節）來針對不同系統進行控制，由此衍生出PD、PI等控制算法，各有其優點，不同的控制策略適用于不同的控制系統，調節偏差快速變化時使調解量在最短的時間內得到強化，有調節靜差，適合調節滯后環節。例如機械臂的位置跟蹤，由于積分環節會在末端收斂時產生震蕩現象，導致收斂慢，為達快速收斂的效果，適合使用PD控制器。

1.2 模型偏差補償與滑模控制SMC簡介

對于許多控制系統，因為復雜性或技術問題，常常無法建立精確的模型，但是這會導致控制效果與預期有較大差距，因此對不確定的模型進行適當的補償具有很大的實際意義[9]，模型偏差補償是一個思想，通過對誤差構成的分析，可以得到一類時變非線性系統的連續軌跡跟蹤問題的模型偏差補償控制方案，可以從仿真的角度得到最好的跟蹤效果。

可變結構控制（Variable Structure Control，VSC）與滑模控制（Sliding Mode Control，SMC）已廣泛應用于具有不確定性和或輸入耦合的系統。其設計理念是獲得一個頻繁切換控制律，將系統驅動到一個指定的和用戶選擇的表面上，稱為滑動表面。當系統處于滑動模式時，其動力學嚴格由滑動表面的動力學決定，因此對參數變化和系統擾動不敏感，魯棒性強，滑模控制另一個優點就是對非線性系統具有良好的控制效果。

機器人作為一個復雜的、時變的、非線性的、具有很多建模不確定性項的系統，單一地PID控已經無法滿足其路徑跟蹤需求，為了提升PID控制的魯棒性，本研究將傳統的比例微分（Proportion Differentiation，PD）控制與模型偏差補償相結合，設計了基于模型補償的機械臂PD型控制器。

圖2 二關節機械臂模型

2 機械臂模型

忽略關節間的摩擦力和其他干擾力，n關節機械臂的動力學方程為：

其中q為n×1的關節位置向量，M（q）為n×n的機械臂慣性矩陣，C（q，）為n×n的離心力與科氏力結合矩陣，G（q）為n×1的重力矩陣，τ為各關節電機輸出的力矩。

機械臂系統動力學有以下特性：（q）-2C（q，）是一個斜對稱矩陣，xT[（q）-2C（q，）]x= 0；慣性矩陣M（q）是對稱正定矩陣[11]。

由于機械臂相鄰關節間存在耦合，無法用一般方法對其進行動力學建模，當前常用的二關節機械臂動力學模型的構建方法主要有：拉格朗日法（Lagrange）、牛頓-歐拉法（Newton-Euler）、凱恩法（Kane）等方法。其中拉格朗日法利用系統能量的微分求出力和力矩，適用于較為復雜條件下的系統建模。

根據拉格朗日法可獲取機器人動力學參數，表示為：

表1 二關節機械臂物理參數表

其中m1為關節1質量，l1為關節一的長度，lc1為關節1質量中心距第一關節長度，I1為關節一的轉動慣量，me為質量，lce為質量中心距第二關節距離，δe為質量中心與第二桿之間的夾角。

3 基于模型補償的PD機械手控制器設計

S函數（S-Function）是一種由用戶自定義功能的Simulink模塊。利用S-function也可以定義自己的微分方程、差分方程、離散系統方程。當Simulink自帶模塊不足以滿足需求時，我們可以利用S函數來編寫所需的功能模塊，從而擴展Simulink的功能。

S函數相當于在Matlab中提供了一個模板程序，用戶通過修改模板程序，根據需求在各個子函數中編寫對應程序，即可自定義S函數模塊的功能[10]。

S函數通過flag標志來控制運行順序，共包含6個子程序，分別是：

①mdlInitializeSizes初始化；

②mdlDerivatives（t，x，u）計算連續狀態的微分；

③mdlUpdate（t，x，u）更新離散狀態、采樣時間與最大步長；

④mdlOutputs（t，x，u）計算S函數輸出；

⑤mdlGetTimeOfNextVarHit（t，x，u）計算下一個采樣時間；

⑥mdlTerminate（t，x，u）。

根據Lyapunov第二方法來設計控制器，可以定義機械臂位置誤差為，其中q=[q1q2]T，q=[q1q2]T。Λ為一個2×2的正的常數比例矩陣，-

設計基于模型補償的PD型控制律為：

其中KD為正定的微分矩陣。

構造Lyapunov函數：

對其求導得：

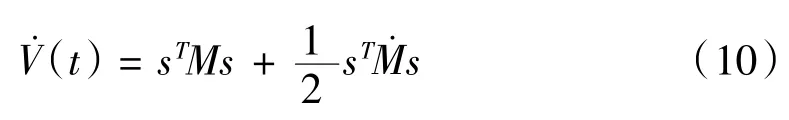
將 式（3）（4）代入上式可得：

由前文可知：

xT[]x，KD為正定的微分矩陣，則有：

所以V˙（t）為半負定的，當且僅當s=0時，V˙（t）=0，根據LaSalle[11]定理可知系統收斂。

4 基于Matlab/Simulink的仿真

為驗證以上控制模型，在Matlab2020b中搭建了控制系統的仿真模型，并同時搭建僅基于PD控制的二關節機械臂位置控制仿真模型作為對照。使二關節機械臂按照期望位置qd=[sin（2πt）sin（2πt）]T進行運動。

經過參數整定后，設計用于對照的基于PD控制的二關節機械臂位置控制器參數為，

能達到較好的控制效果。

圖3 關節1的位置和速度跟蹤

圖5 關節力矩輸出

圖4 關節2的位置和速度跟蹤

從以上仿真結果可以看出，基于模型補償的PD型控制方法位置跟蹤收斂時間在0.4 s，而傳統PD控制則是1.9 s左右，且穩態跟蹤誤差可以精確到控制到1%以內，而傳統PD控制關節1位置跟蹤則存在滯后性，關節2位置跟蹤誤差則達6%。無論是調節時間還是穩態誤差，都是所提方法跟蹤性能更好。綜上，所設計的控制器對兩個關節的位置和速度跟蹤性能都是令人滿意的，這表明控制器能夠達到控制要求。

5 結語

通過PD控制與滑模控制相結合設計的基于模型補償的機械手PD控制器，并在Matlab/simulink中建立仿真模型，采用S函數編寫各個模塊進行仿真，同時建立傳統的機械臂PD位置控制模型，與所設計的控制器進行對比，仿真結果表，該控制器跟蹤性能優于傳統的PD控制器，能夠很好地跟蹤預定的關節軌跡。