決策樹算法在高校畢業生就業預測中的應用
——以普洱學院為例＊

普洱學院 王嬌

近幾年，我國大學畢業生數量不斷增多，畢業生的就業問題是當前高校工作的重點。運用行之有效的方法分析預測就業趨勢具有實際意義。該文將數據挖掘技術用于應用型高校畢業生就業情況的分析中，利用普洱學院畢業生就業數據，引入C4.5 算法，計算信息增益率指標，構建分類決策樹，建立畢業生就業預測模型。通過對模型的測試，構建模型預測結果混淆矩陣，得到預測模型的準確率達到83.33%。

就業是民生之本，對經濟發展有著重要的作用[1]。近些年，高校招生規模不斷擴大，隨之大學畢業生群體也在不斷地壯大。2022年高校畢業生總規模達到1076 萬人，創下歷史新高，且受到新冠疫情的影響，畢業生就業壓力隨之增大，且需要面臨更加復雜嚴峻的形式。為適應社會發展，國家相關部門支持各大高校轉型為應用型大學，鼓勵培養應用型人才。國家對應用型高校畢業生就業工作十分地重視。

在信息收集和分析手段有限的年代，不僅無法全面了解畢業生的在校信息，而且也無法精準、及時的掌握畢業生就業情況。隨著現代社會信息化程度越來越高，大數據技術應用到了各行各業中。在許多方面，數據挖掘技術被廣泛地運用在教育教學中，如：關聯分析技術、決策樹算法、隨機森林算法、神經網絡等技術。利用數據挖掘技術發現數據中蘊藏的有價值信息，指導實際工作。

教育及就業相關的數據庫中的數據量迅速增長，各省大學生就業信息管理系統逐漸建立完善，對大學生在校學習情況及畢業就業情況能夠較全面的掌握。但是，目前對于現有的信息管理系統，管理者主要還是側重于查詢、更新、存檔等功能，并未充分利用管理系統中的數據進行深入分析[2]。如何挖掘應用型高校畢業生就業數據的價值，而數據挖掘技術恰恰就是最好的解決方法[3]。在數據挖掘中，分類是一項非常關鍵的分析手段，實現分類的方法有多種，如：異常檢測、決策樹、隨機森林等。

利用現有就業數據進行合理預測，將為應用型高校在制定學生培養計劃和能力提升方面提供理論依據。本文基于決策樹C4.5 算法，對普洱學院畢業生的就業數據進行分類研究，通過設置英語成績、計算機成績、專業課成績、是否掛科、是否就業等變量，建立關于就業的C4.5 決策樹模型。

1 相關概念

1.1 決策樹

決策樹是數據挖掘分類算法中常見分類方法，通過有效的監督學習，輸出容易理解的結果，可用于分類及預測。1966年，Hunt 等人在其研發的概念學習系統中首次提出決策樹的概念[4]。自1986年Quinlan J R 提出了ID3 算法后，該算法在機器學習等多領域都得到了很大的發展，因此在數據挖掘和應用中具有較好的前景。決策樹在各個領域中運用非常廣泛，如醫學疾病分類、氣象分類、銀行用戶分類、電子郵件分類等。利用訓練集數據集構建分類決策樹后，可以利用測試集數據集對模型的分類進度進行檢驗，以此確定所構建的模型是否適用于分析該問題。決策樹是一種通過從上到下的遞歸形式，以樹狀形式呈現分類規則和分類結果的算法，在樹的每一個節點上通過對比并選擇屬性值，以此判斷該節點向下的分支，在樹的葉節點處得到分類結果[5]。決策樹分類結果易于使用者理解，算法實現容易，它不需要使用者具備更多的數據挖掘知識，便可通過決策樹誠信的樹形結果進行分析、理解。實現決策樹常見的算法包括：ID3、C4.5、CART 和CLS 等[6]。

1.2 ID3 算法

ID3 算法是由J.Ross Quinlan 提出。該算法把信息論中的一些概念引入其中，以信息熵和信息增益作為基礎，以此作為數據屬性劃分的標準，最終實現對數據集的分類。

1.2.1 信息熵

Shannon 在1948年把熱力學中的熵引入信息論，提出了信息熵的概念，又被稱為香農熵。他用數學公式的形式闡明了概率與信息冗余的關系。利用熵可以把隨機變量的不確定程度描述出來。

設X為離散型隨機變量，概率分布為：

p(xi)=P(X=xi),i=1,2,3,…,n

Shannon 把隨機變量X的熵H定義為：

隨機變量X的熵依賴于X的分布，約定0 ·log0 = 0。

1.2.2 條件熵

條件熵H(Y|X)是在X已知的條件下Y的不確定性，定義為：

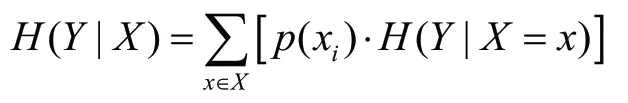
1.2.3 信息增益

信息增益是在X已知的條件下，Y的熵值較沒有任何條件確定時減少的程度[7]。定義為：

Gain(Y,X)=H(Y)-H(Y|X)

信息熵與條件熵相減就是信息增益。一般，信息增益越大，表示所用劃分屬性獲得的“純度增加”越大。ID3 算法以此選擇決策樹的劃分屬性，一般用于處理離散型數據。從信息增益計算公式中可以看出，該算法具有傾向于取值較多的特征[8]。

1.3 C4.5 算法

J.Ross Quinlan 對ID3 算法進行改進提出了C4.5 算法，信息增益率作為該算法劃分屬性的判斷指標[9]。ID3算法的所有優點都能在C4.5 算法中體現出來。同時，C4.5 算法可以處理離散變和連續變量，消除了ID3 算法的多值特征傾向[10]。與ID3 算法相比，C4.5 算法在效率和準確程度上也有很大的提高[11]。

信息增益率在信息增益的基礎上兼顧了為獲取信息增益所付出的“代價”，消除了特征取值較多時帶來的影響，等于信息增益除以特征的固有值，定義為：

確定各屬性的信息增益率，選取信息增益率最高的屬性作為根節點，以此標準進行迭代，最終構建出分類決策樹。

本文利用C4.5 算法對畢業生的就業相關數據進行分類分析。主要探討該算法在應用型高校畢業生就業預測中的可行性。通過建立就業預測模型，希望為高校開展就業指導工作提供幫助。

2 基于決策樹算法在應用型高校畢業生就業預測中的應用

2.1 數據來源及梳理

本文選取畢業生中英語成績、計算機成績、專業課成績、是否掛科、是否就業5 個變量，隨機抽取普洱學院數學與統計學院12 名畢業生的相關數據建立決策樹模型。為方便建模，對采集到的數據進行預處理。從教務系統中導出學生各科在校成績，對各類型科目取平均成績，如：英語成績為大學外語1 和大學外語2 的平均值。且認定85 分以上為優秀，70 ～85 為良，70 分以下為差，數據如表1所示。

表1 畢業生情況表Tab.1 Graduate fact sheet

2.2 模型構建

2.2.1 計算類別的信息熵

在樣本數據中，9 人就業，3 人未就業，故P就業=9/12，P未就業=3/12。由信息熵計算公式可得：

2.2.2 分別計算每一個屬性劃分方式的條件熵

以英語成績為例，令隨機變量X 為英語成績，則X取值為{優、良}，其概率分別為根據條件熵計算公式可得：

同理可計算出屬性“計算機成績”“專業課成績”“是否掛科”的條件熵分別為：0.6701、0.7704、0.2704。

2.2.3 計算信息增益

根據信息增益計算公式可得：

Gain(Y,X) =0.8113-0.4686=0.3427

同理可計算出屬性“計算機成績”“專業課成績”“是否掛科”的信息增益分別為：0.1412、0.0409、0.5409。

2.2.4 計算屬信息增益率

根據信息增益率計算公式可得：

同理可計算出屬性“計算機成績”“專業課成績”“是否掛科”的信息增益率分別為：0.1020、0.0344、0.5890。

2.2.5 建立決策樹模型

由計算結果可知，屬性“英語成績”的信息增益率最高，故選擇該屬性為分裂屬性作為根節點。分裂后，“英語成績”為優的條件下，類別是“純”的，即畢業生就業情況類別均為就業，故把此定義為葉節點。從“英語成績”為良向下繼續進行分裂，依次按照2.2.1 ～2.2.4 的方法進行計算，構建出C4.5 算法的決策樹，如圖1所示。

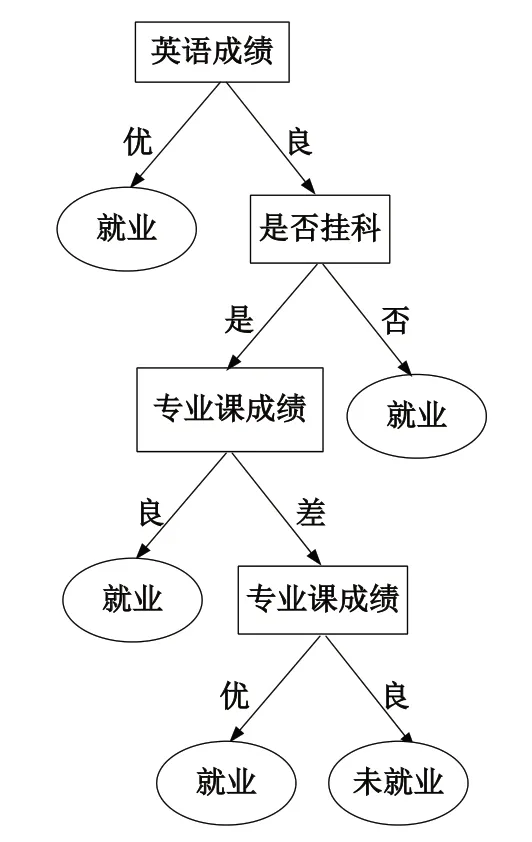
圖1 畢業生就業預測模型圖Fig.1 Graduate employment prediction model diagram

2.2.6 模型預測

為驗證決策樹模型的精確度，根據圖1的決策樹，對樣本數據精選了驗證，利用驗證結果得到預測混淆矩陣，如表2所示。結果表明，該決策樹模型精確度達到83.33%，模型能夠得到較好的預測結果。

表2 預測結果表Tab.2 Forecast result table

3 結語

本文采用決策樹C4.5 算法，對普洱學院畢業生的就業數據進行了分析，得到了預測精度較高的決策樹分類模型。預測模型能夠處理定性數據和定量數據，能夠很好地適應就業相關數據的分析，模型構建簡單、快速，結果直觀，便于理解。能夠為應用型高校畢業生就業情況的預測提供有效的預測，為高校幫扶畢業生就業提供一定的理論基礎。本文不足之處在于，訓練樣本較少，可能存在一定的偏差，在進一步地研究中將選取更大的訓練樣本，考慮更多的相關屬性。