基于聯合稀疏表示和同時稀疏近似的并行坐標下降去噪算法
何選森 徐 麗
1(廣州商學院信息技術與工程學院 廣東 廣州 511363)2(湖南大學信息科學與工程學院 湖南 長沙 410082)
0 引 言
信號的稀疏表示(Sparse representation)[1]是將信號分解為超完備字典(Over-complete dictionary)[2]少量原子的線性組合。由于觀測信號存在噪聲,信號處理的任務之一是去噪(Denoising)。而稀疏表示具有潛在的降噪能力[3],聯合稀疏表示(Joint Sparse Representation,JSR)[4]和同時稀疏近似(Simultaneous Sparse Approximation,SSA)[5]已被廣泛地應用于音頻和圖像去噪。收縮(Shrinkage)則是基于稀疏表示的著名降(去)噪技術[6],如經典的小波收縮是利用正交變換實現降噪[7],而新的趨勢是采用超完備變換替代正交變換。另外,基本追蹤(Basis Pursuit,BP)[8]是通過優化將信號分解為字典原子的最佳疊加,從而使表示系數的l1范數(或l0范數)最小化[9],而基本追蹤去噪(BP Denoising,BPDN)[10]對于消除高斯白噪聲是最佳的。隨著超完備字典的發展,迭代收縮(Iterative Shrinkage,IS)算法[11]已成為一種高效的數值技術。Elad[12]提出了四種IS算法以解決BPDN問題,其中的并行坐標下降(Parallel Coordinate Descent,PCD)算法[12]具有最快的搜索速度。文獻[13]對PCD進行了收斂性分析,并引入了一種正則化函數形式,使得PCD能對坐標優化提供解析的解。
對于音頻信號,用PCD分別處理每一幀能夠獲得很好的去噪性能。然而,當信號很長時,分割的音頻幀數量會很大,用PCD對每幀進行降噪使得計算量急劇增加,造成極大的運行時間成本。為此,本文通過構建以信號(矩陣)為操作對象的時域處理框架,提出一種啟發式矩陣型PCD算法(Joint-PCD)。在新的時域框架中,把信號中的每個語音幀看作一個列向量生成信號矩陣,Joint-PCD算法是對一個信號(矩陣)實施降噪,而不僅僅只對一幀處理,因而可以降低算法的運行時間成本。
1 稀疏信號的降噪
若在同一時刻,信號向量x∈RN中只有很少分量是非零的,其他絕大多數分量都為零值,則稱x服從稀疏分布,即x可由幾個單位能量的原子dk的線性組合來近似[14]。由所有原子構成的集合{dk,k=1,2,…,K}稱為字典D∈RN×K。設向量z∈RK是稀疏的,則信號x可以表示為:
x=Dz
(1)
式中:z是由x的K個重構系數組成的列向量。當字典D是正交的,K=N,則表示是唯一的。當字典D是冗余(超完備)的,K>N,則重構每個信號,就有無限多個可能的系數集。正是這種非唯一性提供了表示方法的可選擇性。一種更好的表示法是選擇具有最少的非零系數的解[15]。
s.t.x=Dz
式(2)是尋找欠定(K>N)線性方程組x=Dz的最稀疏解[15]。類似地,式(2)也可以表示為[15]:
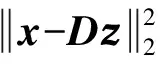
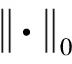
s.t.x=Dz
式中:l1范數是求向量各元素絕對值之和。由于l1范數是l0范數的凸化[15],因此,式(4)也可看作是式(2)的凸化。
對于含噪聲的觀測信號向量:
y=x+v
(5)
式中:x∈RN是不含噪聲的干凈信號;v∈RN是有限能量(表示為δ)的高斯零均值白噪聲向量。對含噪聲信號y進行去噪處理的優化問題可表示為[16]:
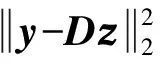
式(6)還可以表示為拉格朗日乘數形式[9]:
式中:λ是正的參數,它用于平衡近似誤差與系數向量稀疏性二者之間的關系。本質上,式(7)就是基于含噪聲信號向量y和超完備字典D的PCD算法的目標函數[12]。
從y中去除高斯白噪聲是對以下函數最小化[12]:
式中:等號右邊的第一項為干凈信號x與觀測信號y之間的對數似然;第二項的ρ(x)表示在x上的先驗值。f(x)的展開式與ρ(x)有關。將式(1)代入式(8)中得到[12]:
式中:1K表示元素為1的K×1列向量。
IS就是解決式(9)所對應的混合l2-lp(p≤1)優化問題的算法。比較式(9)和式(7)可知,在PCD算法中,先驗函數ρ(z)是l1范數,而且PCD的操作對象是向量。
2 新的時域處理框架
用超完備字典原子的線性組合來表示信號向量,就稱為簡單稀疏近似(Simple sparse approximation),在PCD算法中使用的就是簡單稀疏近似。對于很長的音頻信號,其分割的幀數就很多,利用PCD分別處理每一幀將造成算法運行時間成本的劇增。為此,需要將以向量為操作對象的模式拓展成以信號(矩陣)為操作對象的模式。
對多個向量同時稀疏近似理論的分析和研究[17],產生出求解SSA問題的策略[18]。在通信系統中,對于被同一信道噪聲污染的音頻信號,其分割的(幀)向量也都具有相同的分布特性。對不同的幀向量,可以使用同一個字典的不同原子的線性組合來近似計算,即以聯合稀疏的模式促進它們非零分量的耦合。因此,為了同時(或并行)地對一個信號的所有幀(向量)進行降噪操作,需要將傳統的幀處理模式轉變成如下新的時域處理框架。
根據分割規則,將音頻信號分割成一系列的幀,每個幀作為一個列向量生成矩陣,使得信號與矩陣唯一的對應。由于一個矩陣中所有的列向量對應于同一個音頻信號的不同幀,因此這些列向量具有相同的稀疏性。另外,由于每個列向量都受到同一個信道噪聲的污染,因而不同噪聲分量之間也不需要統計獨立。基于這樣的信號矩陣,可以同時處理多個列向量以節省降噪的時間開銷。
3 Joint-PCD啟發式算法
在新的時域處理框架之下,將簡單稀疏近似的概念推廣到同時稀疏近似(SSA),并以此為基礎,將PCD擴展為矩陣型的Joint-PCD算法,其基本原理如下。
令y1=x1+v1、y2=x2+v2分別為干凈信號x1,x2∈RN的含噪聲觀測量,其中v1,v2∈RN為加性噪聲。假設信號x1、x2可以由超完備字典D∈RN×K近似表示為x1=Dz1、x2=Dz2,其中z1,z2∈RK為x1、x2的重建系數。由式(7)可得:
聯合考慮以上這兩個優化問題,則有:
(11)
再令X=[x1,x2]、Y=[y1,y2]、Z=[z1,z2],則將式(11)簡化為如下標準的稀疏編碼問題:
對Z和D二者來說,式(12)不是一個凸優化,但當固定其中一個時,式(12)就成為凸優化問題[4]。本文中,字典D是給定的,而通過優化系數矩陣Z來構造Joint-PCD算法。
式(12)是對兩個信號y1、y2同時去噪的優化問題。顯然,優化式(12)可以推廣到多個信號向量的情況。考慮矩陣形式的觀測信號模型為[19]:
Y=X+V
(13)
式中:X∈RN×P是包含P個向量xi∈RN的干凈信號矩陣;V∈RN×P是P個向量vi∈RN組成的噪聲矩陣;Y∈RN×P是含噪聲觀測信號矩陣。基于聯合稀疏表示(JSR)[4],信號X可以由字典D表示為X=DZ,于是觀察信號矩陣Y為[19]:
Y=DZ+V
(14)
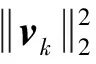
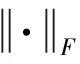
式中:ρ(·)是任意標量函數,而ρ(Z)是矩陣Z稀疏性的懲罰函數。式(16)就是Joint-PCD算法的目標函數。
由式(15)和式(16)可歸納出構造Joint-PCD算法的基本思想。為了限制對觀測信號Y進行逼近的字典原子的總數,需要使Z中非零行向量的數量最小化。為此,從兩方面來考慮。首先,參與對Y近似的字典原子總數越少越好;其次,每個參與近似的原子要對盡可能多的Y的列向量做出貢獻。也就是說,系數矩陣Z是稀疏的,即它的大多數行向量都是零向量,而Z的每個非零行向量都應該有盡可能多的非零元素。基于此,將稀疏性懲罰函數ρ(Z)設置為行l0準范數(Row-l0quasi-norm)的松弛版:
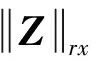
把式(17)代入到式(16)中,則觀測信號矩陣Y的降噪任務變成為混合范數的優化問題:
同樣地,由式(12)可知,懲罰函數ρ(Z)是矩陣Z的l1范數。在本文中,對ρ(Z)的l1范數使用偶對稱函數:
式中:zij是矩陣Z的第(i,j)個元素。
這里需要提示,在式(12)中Z和Y都是由兩個向量構成的矩陣,然而,在下文中,將兩個向量情況推廣到多個向量的情況,即式(12)中的Z和Y是由P(P≤2)個列向量組成的矩陣Z∈RK×P和Y∈RN×P,而不僅僅是由2個列向量組成的矩陣Z∈RK×2和Y∈RN×2。
U(D,Y,Zk)=diag-1{DTD}DT(Y-DZk)+Zk
(20)
一般地,超完備字典D的列是歸一化的,即diag-1(
DTD)=I,其中I是單位矩陣,則可將式(20)簡化為:
U(D,Y,Zk)=DT(Y-DZk)+Zk
(21)
矩陣Z的更新迭代值Zk+1為:
Zk+1=Zk+μQk
(22)
式中:μ是迭代步長參數。
Qk=S[U(D,Y,Zk),λ]-Zk
(23)
式中:λ是收縮函數S(·)的閾值。從四種IS算法的推導過程[12]可知,式(23)中的收縮函數S(·)是一個軟閾值函數,其定義為:

式中:θ為軟收縮函數S(·)的閾值。
另外,Joint-PCD算法的性能會受到式(22)中步長參數μ影響。對足夠小的μ>0,步長要保證懲罰函數ρ(·)的可行下降。本文使用線搜索[11]來尋找最佳的步長μ值。線搜索作為一維優化,它用于解決以下的問題:
式中:ρ(·)可以是矩陣的rx范數,也可以是矩陣的l1范數。
若信號矩陣Y退化成一個列向量y,系數矩陣Z也退化成一個列向量z,則Joint-PCD算法退化為PCD算法。因此,將Joint-PCD稱為啟發式算法。
在音頻信號處理中,經常使用離散余弦變換(DCT)字典和Gabor字典。一個窗口式DCT字典為DDCT=[d1,d2,…,dK],它的第k個原子定義為[20]:
一個窗口式Gabor字典為DG=[d(k,φ)](k,φ)∈Ψ,其原子以連續的參數集Ψ=[1,K]×[0,2π]為索引,其定義為[20]:
式中:1≤k≤K,0≤t≤N-1,N是音頻幀的長度,K是字典的尺寸;wd是加權窗口;φ是相位。Gabor字典連續索引原子d(k,φ)的分解可以用離散字典中的原子對來表示[20]。
式中:原子對是相同頻率且相位為零的余弦和正弦對。為簡化計算,詞典的列都做歸一化處理,如Gabor字典的正弦和余弦原子都使用對應的單位范數版本。
綜上所述,對啟發式Joint-PCD算法描述見算法1。
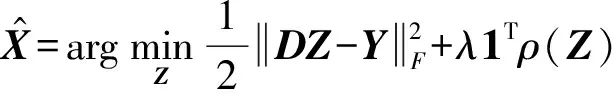
輸入:觀測矩陣Y,字典D,閾值λ,函數ρ(·),迭代次數M。
Begin:設置k=1,迭代開始。
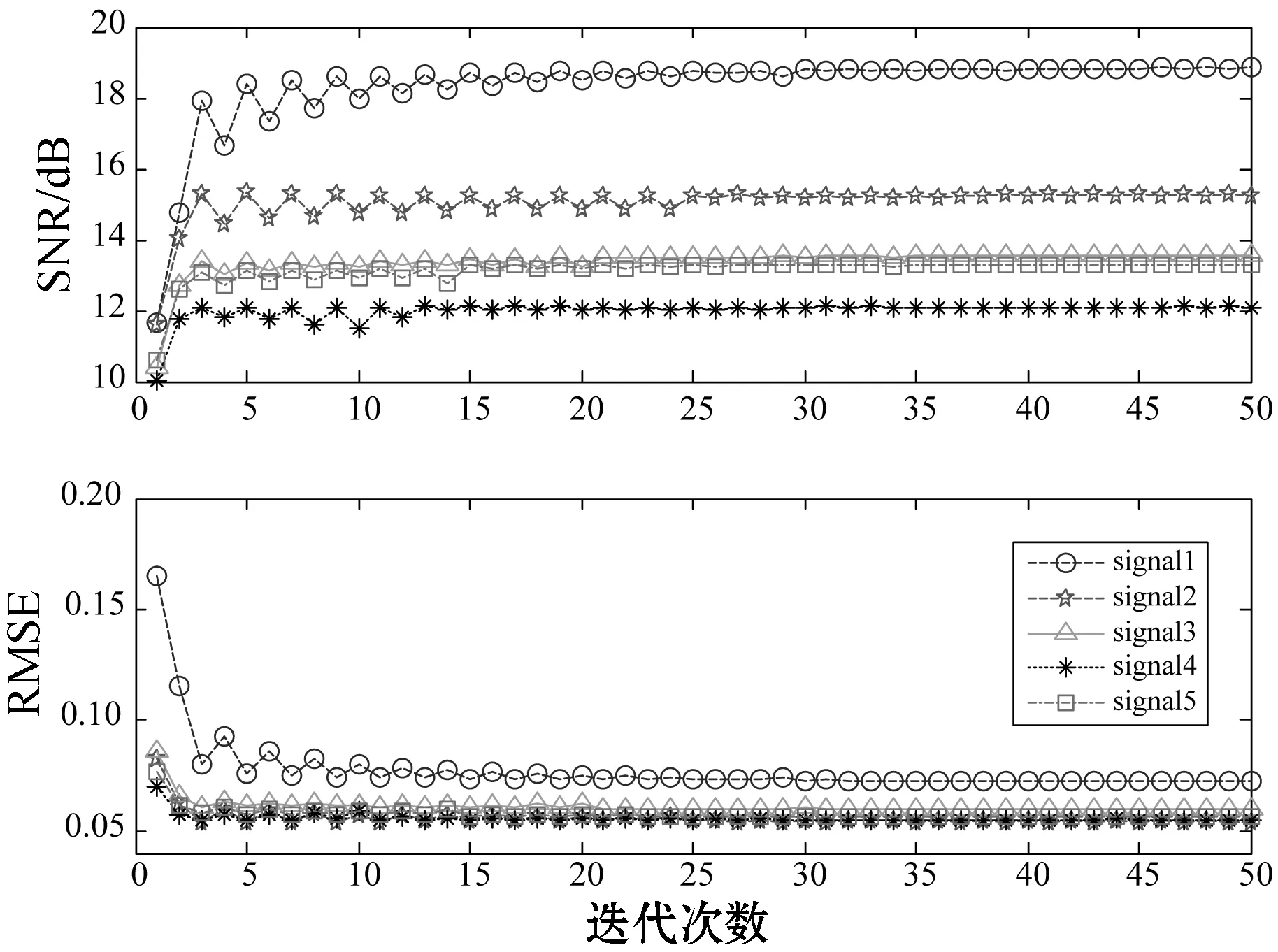
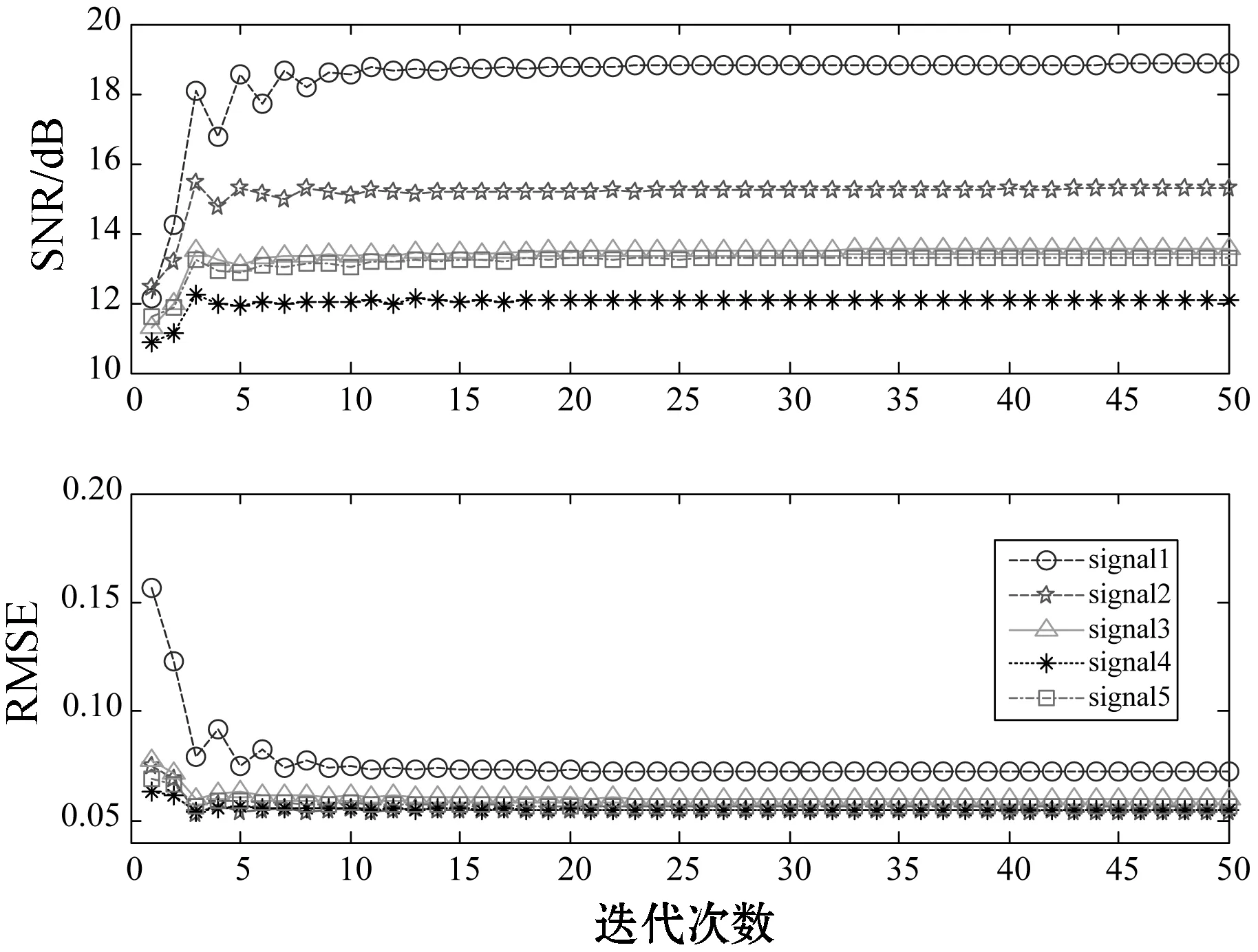
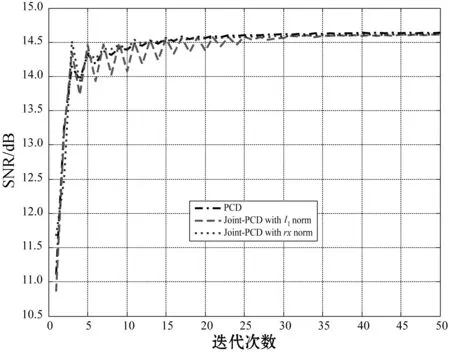
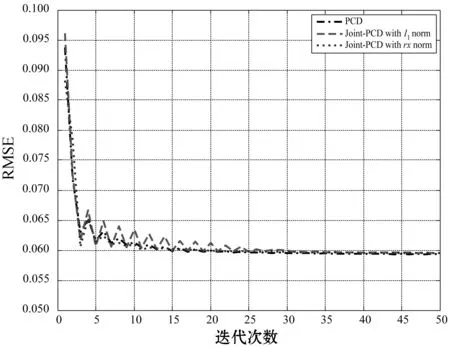
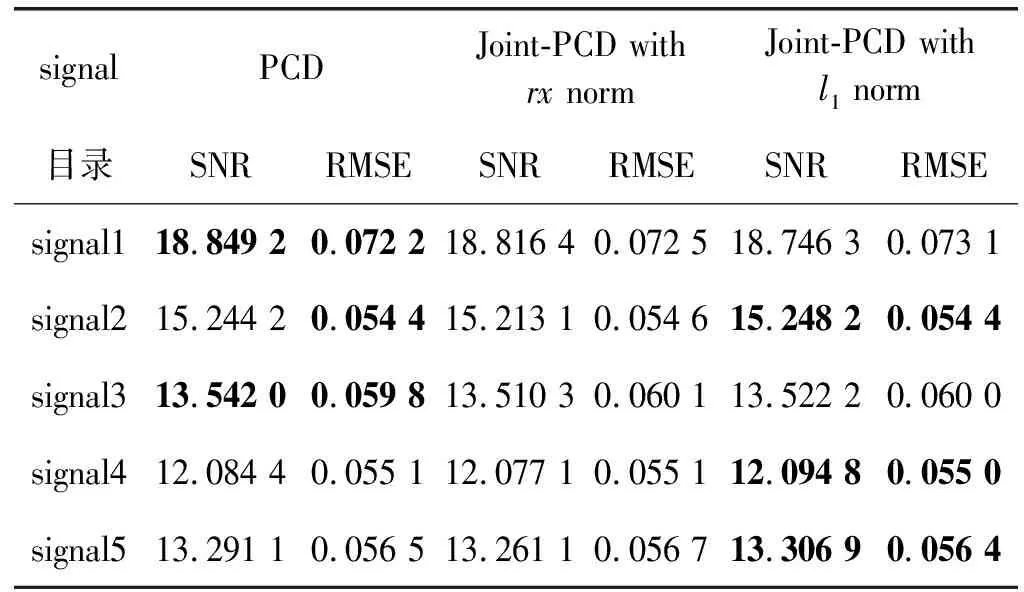
ifk 誤差:計算E=Y-DZk; 映射:計算ET=DTE; 收縮:計算ES=S(ET+Zk,λ); 線收縮:尋找μ0以獲得Zk+μ(ES-Zk)的下降; 放松:更新迭代Zk+1=Zk+μ0(ES-Zk); Next:k←k+1; End 為了驗證Joint-PCD算法降噪的有效性,對Joint-PCD和PCD在音頻信號降噪性能上進行對比分析。不同算法的仿真環境是完全一樣的,以便得到公平的結論。 仿真平臺為筆記本電腦,其CPU為Intel(R) Celeron(R) 1007U CPU-1.50 GHz,內存4 GB,操作系統為Windows 10。仿真軟件平臺為MATLAB 9(R2016a)。 降噪的性能用信噪比(signal to noise ratio,SNR)和均方根誤差(root mean square error,RMSE)來衡量: 測試用的五個音頻音樂信源[21]的類型為.wav,信號采樣率為44.1 MHz。每個信源的樣本數為L=216=65 536。五個信源均服從超高斯分布,它們之間的區別體現在具有不同的峭(峰)度(kurtosis)值。信源X=[x1,x2,x3,x4,x5]T的歸一化峰度值分別為2.400 8、4.776 6、1.052 8、4.690 2、3.133 7,其對應的時域波形如圖1所示。 圖1 五路音樂音頻源信號的波形 降噪的仿真過程如下。音頻信源與高斯噪聲相加生成含噪聲信號。首先,每個含噪聲時域信號乘以長度為64的漢明窗生成語音幀,連續兩幀之間的重疊樣本數為32,即每幀的前后各有16個樣本與相鄰幀的樣本重疊。分幀過程是通過使用Voicebox[22]中的MATLAB函數enframe來實現。然后,將PCD和Joint-PCD算法分別應用于分割后的信號以進行降噪。每次使用PCD是對音頻信號的一幀進行處理;而使用Joint-PCD算法每次是對一個信號(而不僅是一幀)進行處理。最后,重建降噪后的信號,即每個降噪的幀乘以逆漢明窗,并且在相鄰兩幀重疊的樣本中,分別在兩邊去除50%的樣本,僅保留每一幀的中間部分的樣本,將經過處理的各個片段簡單串聯起來即可得到重新合成的音頻信號。 在PCD算法中,需要給定軟收縮函數S(·)的閾值λ。常用的閾值規則為全局閾值(universal threshold)[7]和最小最大閾值(minimax threshold)[7]。本文采用全局閾值的設置,滿足以下條件: 式中:L是信號的樣本數量;σ是高斯噪聲的標準差。顯然,要確定閾值λ,則必須先確定噪聲的強度σ。 為了確定噪聲強度對降噪性能的影響,采用經典的小波降噪方法進行仿真。對5個信源X加噪聲形成觀測信號Y,當Y的信噪比分別為10、15、20時,利用小波重復進行100次降噪實驗,并計算在每次實驗中5個信號的平均SNR值和RMSE值,其結果如圖2所示。 圖2 5個信號的平均SNR和RMSE值 從圖2可知,隨著輸入SNR的降低(噪聲強度的增大),小波的降噪性能變差。當輸入SNR為10時,經過降噪后5個信號的平均SNR小于9.8,即降噪后的信噪比小于輸入的信噪比。對音頻信號來說,這是一個非常惡劣的環境。 為了便于分析,對不同的輸入SNR,計算出每個信源被施加高斯噪聲的強度σ。其結果如表1所示。 表1 輸入SNR與噪聲強度σ的對應關系 從表1中的數據可知,由于每個信源的幅度(功率)不同,對同一個輸入SNR值,其對應于不同信源的噪聲強度也是不同的。對于輸入SNR為10的情況,信號x2、x3、x4、x5上施加的噪聲強度接近0.1,但信號x1上施加的噪聲強度為0.2。為獲得一個統一的噪聲強度,在下面的仿真中,5個信源都被施加σ=0.1的高斯噪聲形成觀測信號。 給定噪聲強度后,再來確定軟閾值λ。由于信號采樣點數為L,則(2log2L)1/2=4.709 6,由文獻[7]可知,在給定σ=1的情況下,其參考的閾值為λ*=3.31。將真實的σ=0.1代入可得λ≤σ(3.31=0.331,這也只是λ的取值范圍,還需要通過仿真來尋找PCD算法最佳的閾值λ。仿真條件為:每個含噪信號都被分割成長度為64的幀,PCD的迭代次數設置為M=5,閾值λ從0.050到0.331變化,更新步長為0.01,每個λ值做一次實驗,超完備字典是DCT和Gabor。各個信號的性能指標SNR和RMSE如圖3所示。 (a) DCT (b) Gabor圖3 每個信號對不同λ的SNR和RMSE值 從圖3可知,無論是DCT還是Gabor詞典,當λ=0.1時,每個信號的SNR達到最大值,而RMSE也達到對應的最小值。因此在PCD算法中,取λ=0.1作為最佳的閾值。另外,從圖3還可看出,采用不同的超完備字典,PCD算法的降噪性能是有差異的。為了比較DCT和Gabor的性能,將迭代次數設置為M=15,并分別計算PCD對每個信號在每次迭代中的SNR和RMSE值。其結果如圖4所示。 圖4 每個信號對不同字典的SNR和RMSE值 為便于分析,僅觀察信號1(signal1)的情況。從圖4可知,使用Gabor字典的SNR和RMSE值都優于DCT字典對應的指標。其他信號的SNR和RMSE值也有相似的關系。為此,在PCD和Joint-PCD算法中,使用Gabor字典。 另外,在算法的參數中,還需要確定懲罰函數ρ(·)及迭代步長μ的值。在下面的仿真中,對于PCD算法,采用向量的l1范數求解式(7);對于Joint-PCD算法,采用矩陣的l1范數求解式(12),采用矩陣的rx范數求解式(18)。為了提高算法的性能,各算法的步長μ(0<μ<1)采用MATLAB函數fminbnd通過在線搜索最優的μ值作為其迭代步長。這樣就完成了PCD和Joint-PCD算法中所有參數的設置。 在對算法去噪性能的比較過程中,為方便起見,把rx范數和l1范數的Joint-PCD分別表示為Joint-PCD withrxnorm和Joint-PCD withl1norm。 關于算法的性能,從兩個方面對PCD和Joint-PCD進行比較。(1) 在相同條件下算法所消耗的運行時間成本;(2) 去噪的性能指標值SNR和RMSE。在這個仿真實驗中,將算法的最大迭代次數M設置為50以進行全面的考察。其運行時間如圖5所示。 圖5 算法的運行時間比較 可以看出,算法的運行時間隨迭代次數的增加基本上呈線性增長。顯然,rx范數和l1范數的Joint-PCD算法的運行時間增長率幾乎是相同的;而PCD算法的運行時間增長率卻遠遠大于Joint-PCD的增長率。 圖6分別給出了PCD算法、Joint-PCD withl1norm和Joint-PCD withrxnorm算法在該仿真中去噪性能指標值SNR和RMSE的波形圖。 (a) PCD (b) Joint-PCD with l1 norm (c) Joint-PCD with rx norm圖6 PCD和Joint-PCD算法對每個信號的SNR和RMSE值 可以看出,PCD與Joint-PCD算法的降噪性能幾乎是完全相同的,而且經過大約25次迭代,三種算法的降噪指標SNR和RMSE值都逐漸收斂到其穩定值。 為了比較算法的平均降噪性能,將每種算法對5個信號的平均SNR和平均RMSE值繪制在圖7中。 (a) (b)圖7 5個信號的平均SNR和RMSE指標 可以看出,PCD和Joint-PCD算法的平均SNR和RMSE值在算法的初始階段隨著迭代次數的增加具有一定的波動,這是因為每個信號的SNR和RMSE值具有不同的波動范圍。對于PCD和Joint-PCD withrxnorm算法,平均降噪指標大約在經過20次迭代后結束波動,趨于平穩;而Joint-PCD withl1norm算法大約在經25次迭代后其降噪指標趨于平穩。也就是說,PCD和Joint-PCD的平均降噪性都能在25次迭代后收斂到穩定的指標值。 為了從數值上直觀地比較PCD和Joint-PCD在降噪性能上的差異,在以下仿真中,將算法的最大迭代次數M設置為25。表2給出PCD和Joint-PCD的運行時間。 表2 PCD和Joint-PCD算法的運行時間 單位:s 可以看出,l1范數的Joint-PCD運行時間是最少的,而rx范數的Joint-PCD運行時間也僅僅是多了0.379 2 s,因此,兩種Joint-PCD算法的運行時間幾乎是相同的。相反地,PCD算法的運行時間大約是Joint-PCD的4.6倍,這說明在音頻信號的降噪過程中,Joint-PCD算法降低了計算負擔。顯然,與PCD算法相比較,Joint-PCD算法的收斂速度得到了有效的提高。 對于PCD和Joint-PCD算法的降噪性能,采用每個信號在整個迭代過程中SNR和RMSE的平均值來度量。表3給出了每個信號的平均降噪性能指標。 表3 每個信號在整個迭代過程的平均SNR和RMSE值 可以看出,Joint-PCD withl1norm算法對于第2、第4和第5個信號的平均SNR和RMSE值是最優的;而PCD算法僅對于第1和第3個信號的平均指標值是最優的。另外,PCD算法和Joint-PCD算法的平均SNR值的差別僅體現在小數點后面第二位;而算法的平均RMSE值的差別僅發生在小數點后面第四位上。因此,從去噪性能指標的差異性來看,利用Joint-PCD算法代替PCD算法對音頻信號進行降噪處理,其降噪的效果幾乎完全相同。 為了解決PCD算法在實際應用中的計算成本問題,本文定義一種新的音頻信號時域處理框架,將每個被分割的音頻幀作為一個列向量生成信號矩陣。在聯合稀疏表示(JSR)和同時稀疏近似(SSA)的基礎上,利用新的處理框架,提出以矩陣為操作對象的Joint-PCD算法。仿真的結果表明,Joint-PCD算法不僅能夠提供與PCD算法幾乎完全相同的降噪性能,而且Joint-PCD算法提供了更高的計算效率,節約了算法的運行時間成本,從而加快了算法的收斂速度。更為重要的是,與PCD算法相比較,Joint-PCD算法在大規模數據處理和實時信號處理應用方面具有巨大的潛在優勢。4 仿真實驗及結果分析
4.1 仿真環境和性能指標
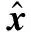
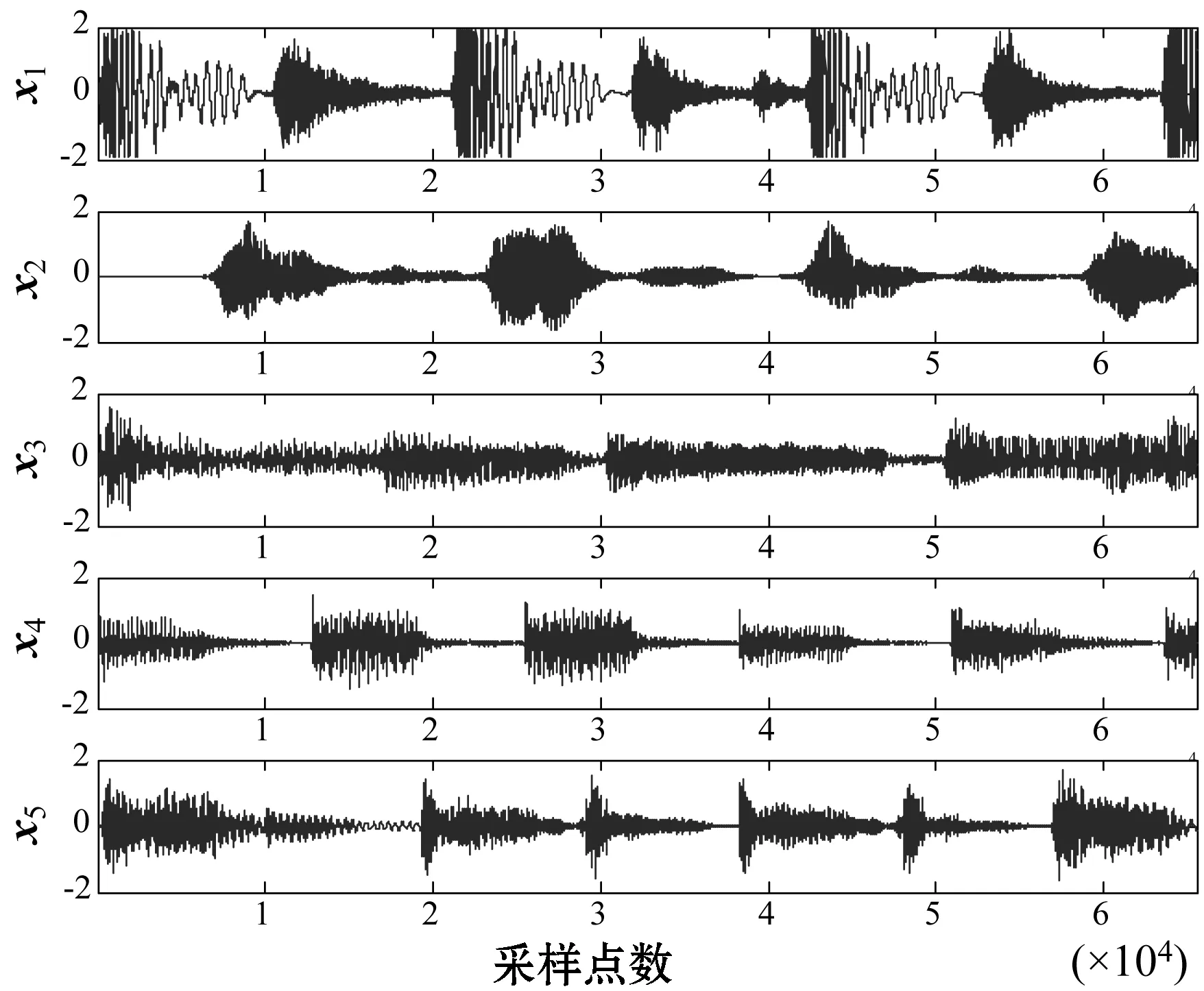
4.2 算法參數設置
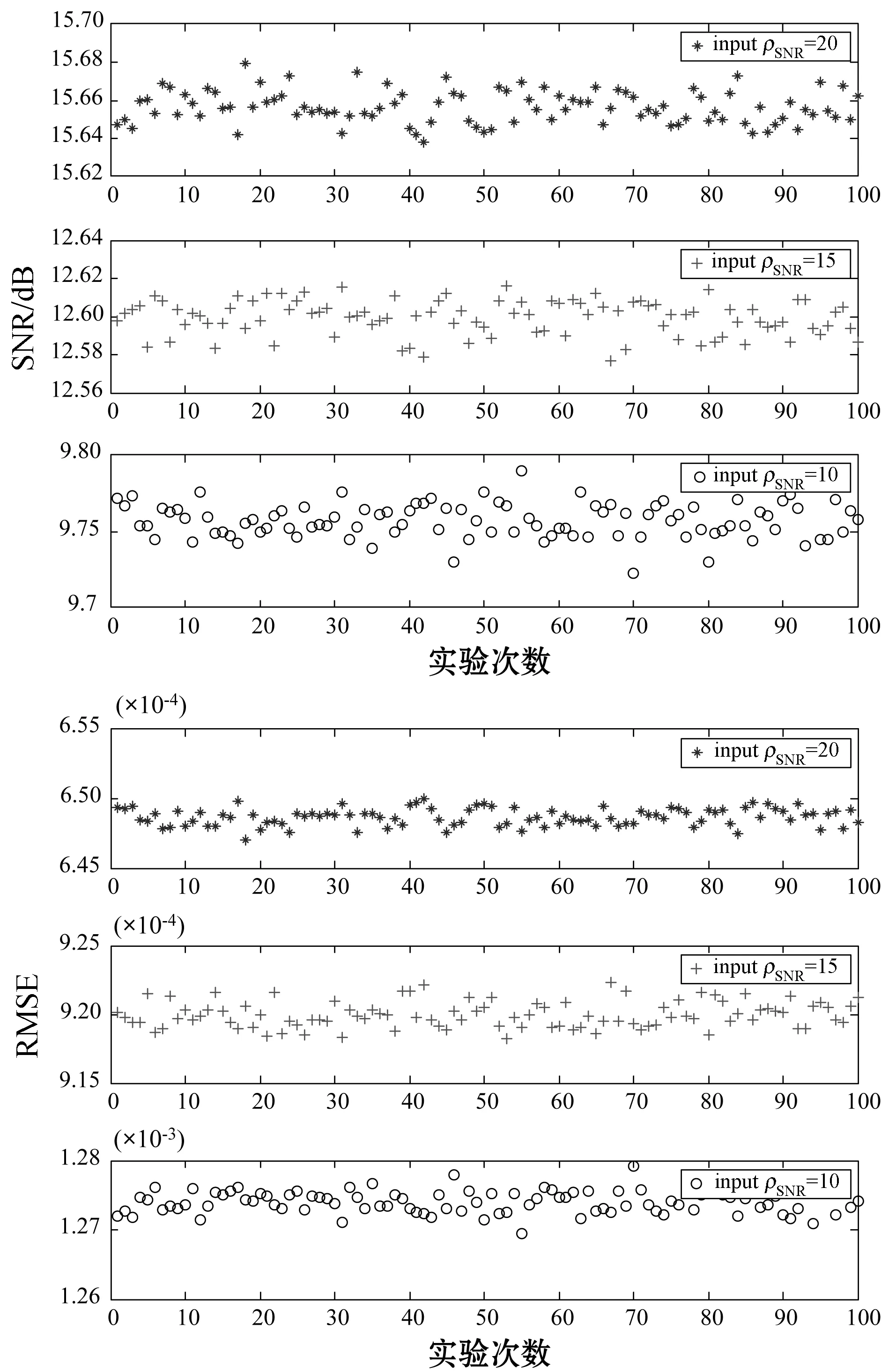
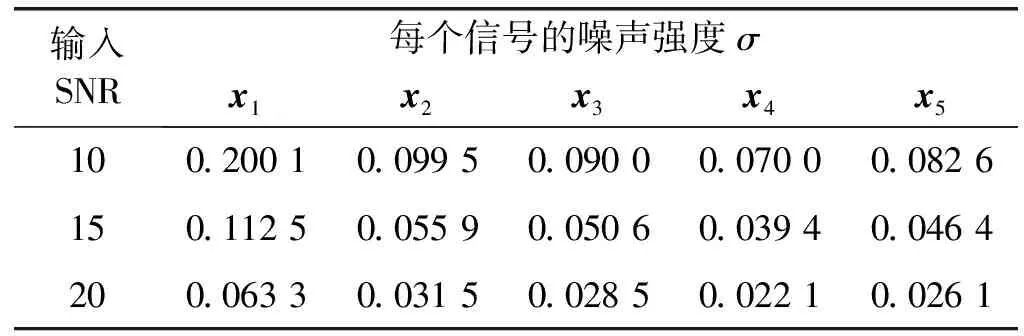
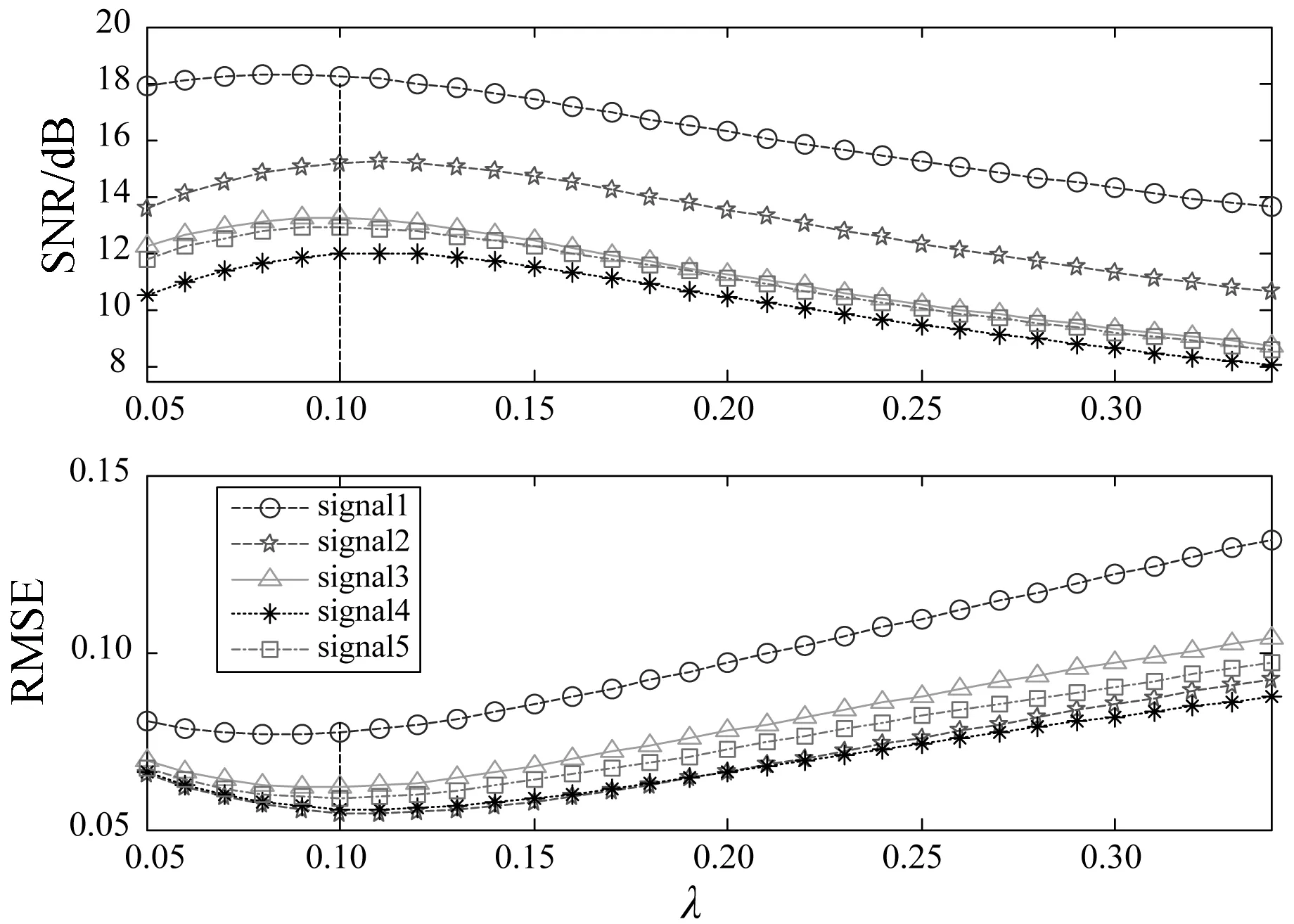
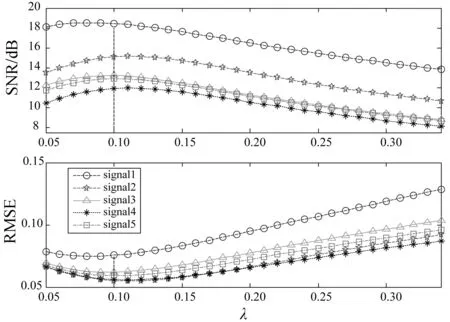
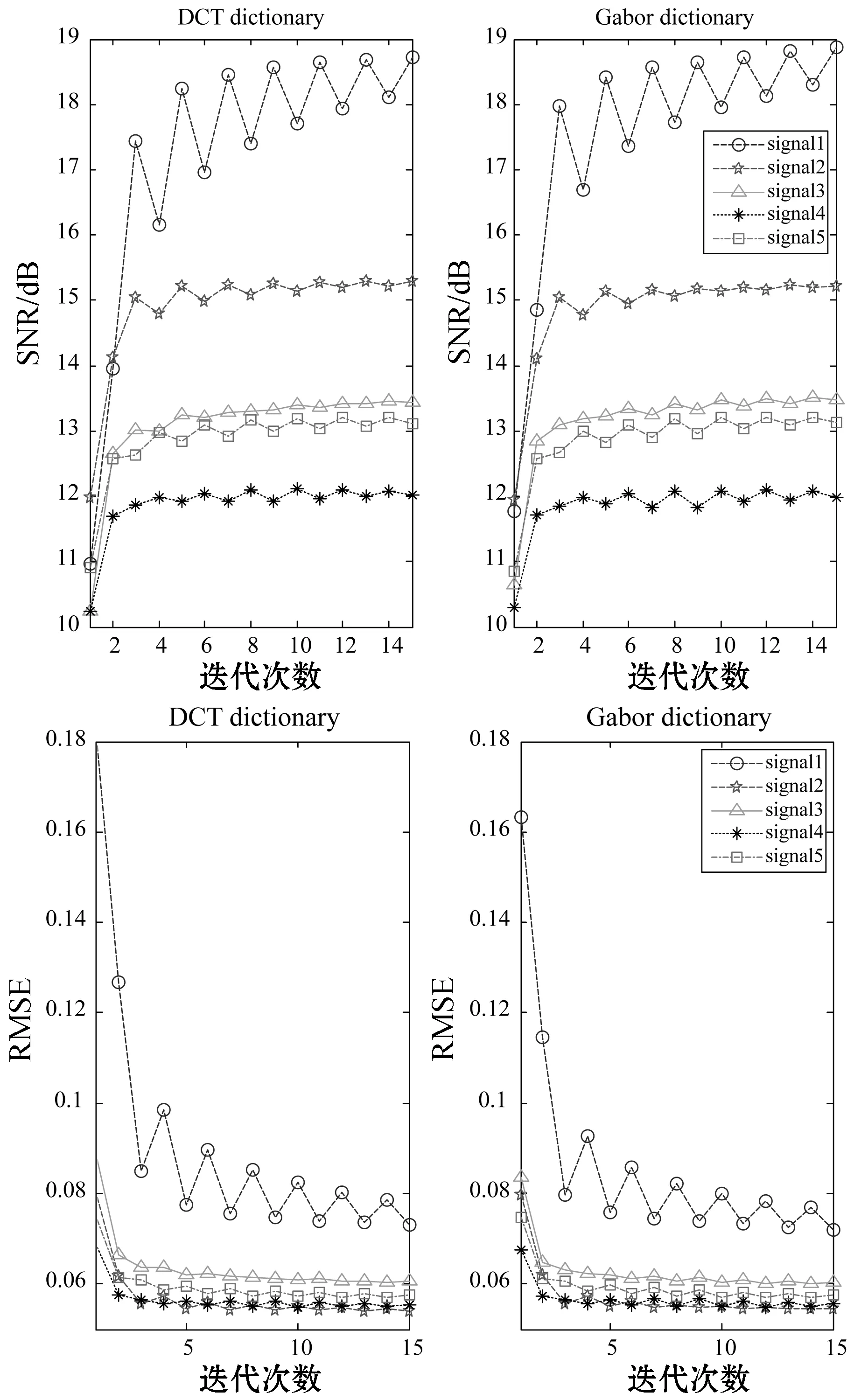
4.3 算法性能比較
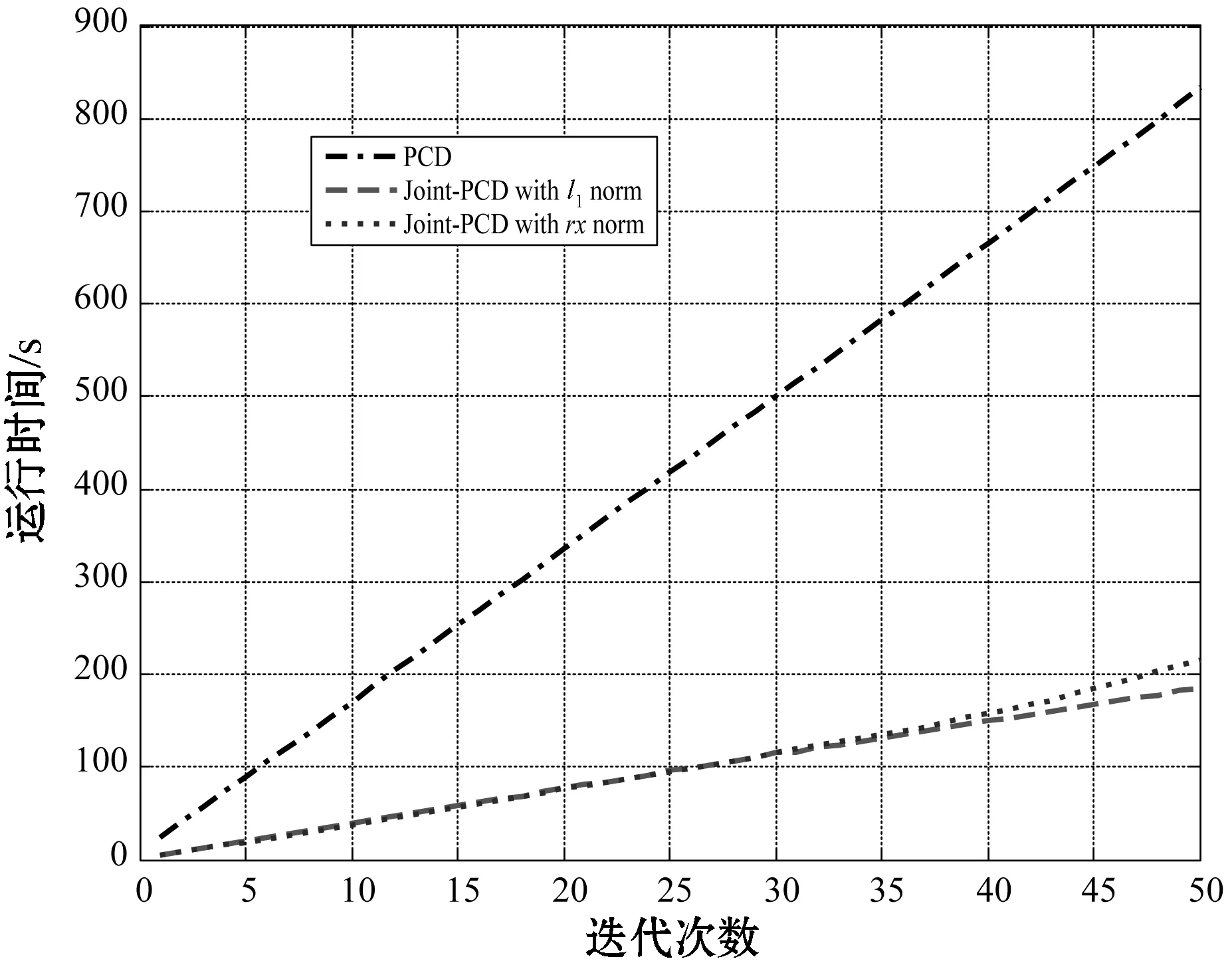
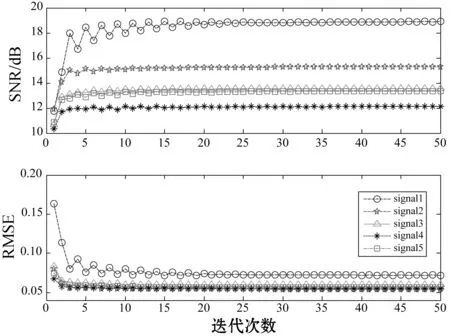

5 結 語

