多工況下電動(dòng)懸浮系統(tǒng)直線發(fā)電機(jī)電磁特性研究

呂 剛 郭曦臨 楚志恒 周 桐 于 旺

多工況下電動(dòng)懸浮系統(tǒng)直線發(fā)電機(jī)電磁特性研究

呂 剛1郭曦臨1楚志恒2周 桐1于 旺1

（1. 北京交通大學(xué)電氣工程學(xué)院 北京 100044 2. 通號(hào)通信信息集團(tuán)有限公司 北京 100044）

直線發(fā)電機(jī)是高速磁懸浮系統(tǒng)中無(wú)接觸車載供電的關(guān)鍵設(shè)備，該設(shè)備在多工況下的輸出特性是發(fā)電能力的主要衡量指標(biāo)。利用空間諧波法對(duì)超導(dǎo)磁體三維磁通進(jìn)行表征，建立直線發(fā)電機(jī)磁動(dòng)勢(shì)分布模型。通過(guò)分析超導(dǎo)磁體與軌道側(cè)壁懸浮線圈間的電磁耦合關(guān)系，得出懸浮線圈電流和懸浮線圈諧波磁場(chǎng)磁通密度的表達(dá)式。進(jìn)一步地，將懸浮線圈諧波磁場(chǎng)作為集電線圈激勵(lì)，推導(dǎo)出適用于多工況下直線發(fā)電機(jī)感應(yīng)電動(dòng)勢(shì)的數(shù)值解析表達(dá)式。最后，通過(guò)將數(shù)值解析結(jié)果與日本山梨線試驗(yàn)數(shù)據(jù)的對(duì)比，驗(yàn)證了磁動(dòng)勢(shì)分布模型和電磁解析模型的準(zhǔn)確性。該工作為高速磁懸浮系統(tǒng)直線發(fā)電機(jī)的設(shè)計(jì)和控制提供了相關(guān)理論基礎(chǔ)。

高速磁懸浮系統(tǒng) 直線發(fā)電機(jī) 電磁解析模型 多工況 感應(yīng)電動(dòng)勢(shì)

0 引言

在更高的運(yùn)行速度、更短的旅行時(shí)間以及更舒適的乘坐環(huán)境等要求下，高速磁懸浮列車被列為重點(diǎn)研發(fā)對(duì)象。高速磁懸浮列車需采用非接觸式供電，而直線發(fā)電機(jī)是高速磁懸浮系統(tǒng)中車載供電的關(guān)鍵設(shè)備[1-4]。其中，電動(dòng)懸浮系統(tǒng)直線發(fā)電機(jī)的電磁特性是其重要研究?jī)?nèi)容。

文獻(xiàn)[5]利用有限元法構(gòu)建發(fā)電機(jī)模型，在發(fā)電機(jī)輸出特性基礎(chǔ)上定義目標(biāo)函數(shù)，并針對(duì)目標(biāo)函數(shù)迭代改變發(fā)電機(jī)配置，得到輸出特性最優(yōu)解。為提高發(fā)電機(jī)運(yùn)行效率、減少能量損失，文獻(xiàn)[6]提出直線發(fā)電機(jī)瞬時(shí)電流控制策略，利用瞬時(shí)電流補(bǔ)償無(wú)功功率，實(shí)現(xiàn)功率因數(shù)為1，從而獲得足夠的電力。文獻(xiàn)[7]是前種方法的改進(jìn)，提出控制單相瞬時(shí)電流來(lái)補(bǔ)償不平衡三相無(wú)功功率的方法，進(jìn)而實(shí)現(xiàn)高功率因數(shù)控制。文獻(xiàn)[8]提出一種零序型集電線圈，用試驗(yàn)驗(yàn)證了速度在300km/h后直線發(fā)電機(jī)能達(dá)到25kW的目標(biāo)集電功率。文獻(xiàn)[9]綜合考慮超導(dǎo)磁體外殼的渦流對(duì)電磁特性的影響，研究發(fā)現(xiàn)，渦流能夠提升懸浮線圈以及集電線圈的感應(yīng)電動(dòng)勢(shì)。文獻(xiàn)[10]發(fā)現(xiàn)，直線發(fā)電機(jī)同時(shí)具備發(fā)電功能以及調(diào)節(jié)轉(zhuǎn)向架阻尼特性，提出通過(guò)控制集電線圈電流的相位進(jìn)而提升轉(zhuǎn)向架阻尼。而文獻(xiàn)[11]提出一種無(wú)傳感器直線發(fā)電機(jī)阻尼器，通過(guò)向直線發(fā)電機(jī)集電線圈注入電流以產(chǎn)生垂直方向電磁力，進(jìn)而衰減列車運(yùn)行時(shí)的振動(dòng)。

目前，針對(duì)電動(dòng)懸浮系統(tǒng)直線發(fā)電機(jī)的研究主要針對(duì)發(fā)電機(jī)高性能優(yōu)化控制策略和列車無(wú)偏移工況下直線發(fā)電機(jī)的電磁特性。對(duì)磁懸浮列車橫向、垂向偏移等多工況下直線發(fā)電機(jī)電磁特性的理論解析研究不足。綜上所述，該文提出一種適用于多工況下直線發(fā)電機(jī)電磁解析模型。利用空間高次諧波法建立超導(dǎo)磁體的磁動(dòng)勢(shì)分布模型，根據(jù)超導(dǎo)磁體、懸浮線圈、集電線圈三者間的電磁耦合關(guān)系，推導(dǎo)出多工況下直線發(fā)電機(jī)感應(yīng)電動(dòng)勢(shì)解析表達(dá)式。揭示了感應(yīng)電動(dòng)勢(shì)、功率隨列車偏移量的變化規(guī)律，解析模型在電動(dòng)懸浮系統(tǒng)直線發(fā)電機(jī)結(jié)構(gòu)設(shè)計(jì)和特征分析上具有優(yōu)勢(shì)，為直線發(fā)電機(jī)設(shè)計(jì)與控制提供了相關(guān)理論依據(jù)。

1 物理模型及原理分析

電動(dòng)懸浮系統(tǒng)直線發(fā)電機(jī)整體結(jié)構(gòu)如圖1所示。超導(dǎo)磁體置于磁懸浮列車轉(zhuǎn)向架兩側(cè)，集電線圈裝于超導(dǎo)磁體外側(cè)，超導(dǎo)磁體和集電線圈隨列車同步運(yùn)行[12]。懸浮線圈固定于軌道兩側(cè)，沿列車線路鋪設(shè)。轉(zhuǎn)向架每側(cè)有4個(gè)超導(dǎo)磁體，相鄰超導(dǎo)磁體極性相反。列車運(yùn)行時(shí)超導(dǎo)磁體產(chǎn)生的磁場(chǎng)被懸浮線圈切割，于是在懸浮線圈中產(chǎn)生感應(yīng)電流和磁場(chǎng)。同時(shí)，集電線圈與懸浮線圈存在相對(duì)位移，集電線圈切割懸浮線圈感應(yīng)磁場(chǎng)，繼而產(chǎn)生感應(yīng)電動(dòng)勢(shì)。磁懸浮列車發(fā)生橫向偏移，車體在軸方向的偏移量為D；而發(fā)生垂向偏移，車體在軸方向偏移量為D。磁懸浮列車未發(fā)生偏移時(shí)：超導(dǎo)磁體頂部與懸浮線圈中心的距離/2=40mm；懸浮線圈與轉(zhuǎn)向架中心的距離為1；集電線圈與轉(zhuǎn)向架中心的距離為2。其中，|1-2|=110mm。

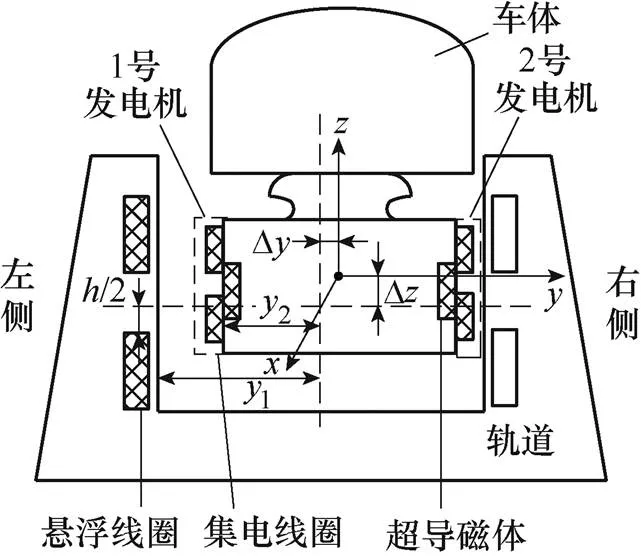
圖1 直線發(fā)電機(jī)整體結(jié)構(gòu)

2 電磁解析模型

2.1 超導(dǎo)磁體磁動(dòng)勢(shì)模型

一組集電線圈有兩個(gè)u相、一個(gè)v相、一個(gè)w相。其中，v相與w相線圈尺寸一致。單個(gè)超導(dǎo)磁體極距下對(duì)應(yīng)一組集電線圈和一組懸浮線圈。超導(dǎo)方向的磁體極距為，長(zhǎng)度為0。懸浮線圈極距為1，長(zhǎng)度為1。u相集電線圈極距為u，長(zhǎng)度為u。線圈的排布關(guān)系如圖2所示。

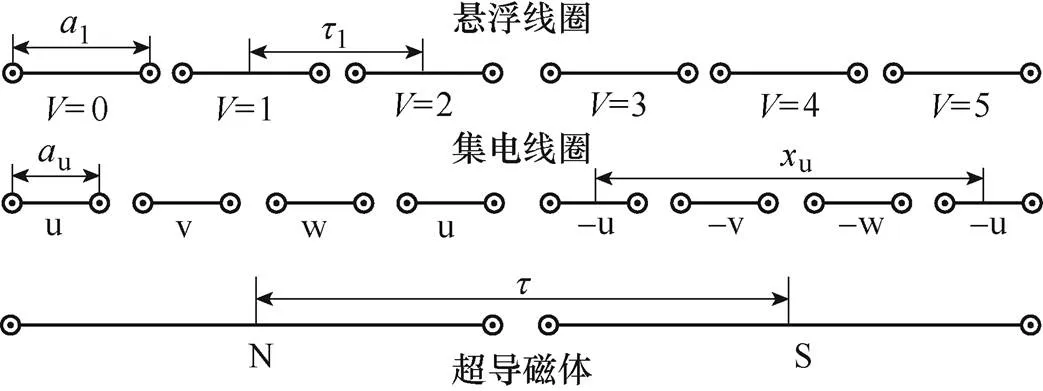
圖2 線圈的排布關(guān)系

利用空間諧波法，在方向和方向分別構(gòu)建超導(dǎo)磁體磁動(dòng)勢(shì)分布模型。其中，軸方向?yàn)閷?shí)際存在的超導(dǎo)磁體，方向假設(shè)存在無(wú)限多的超導(dǎo)磁體[13-14]。超導(dǎo)磁體方向極距為l，超導(dǎo)磁體匝數(shù)為s，單匝線圈電流為s，0為真空磁導(dǎo)率。圖3為超導(dǎo)磁體磁動(dòng)勢(shì)分布模型。

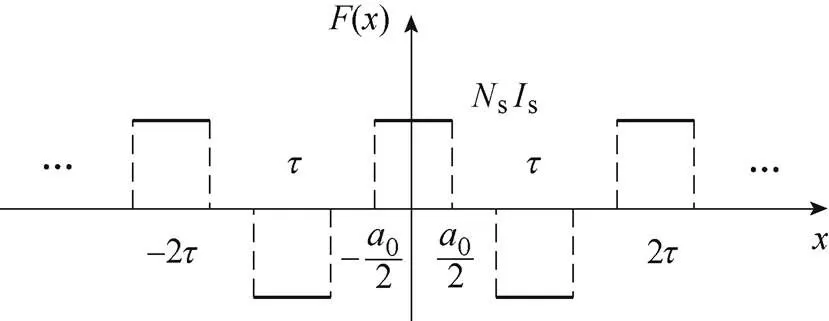
圖3 磁動(dòng)勢(shì)分布模型

將超導(dǎo)磁體磁動(dòng)勢(shì)寫為傅里葉級(jí)數(shù)[15]求和形式，求出軸方向傅里葉系數(shù)f（=1, 2, 3,…）為

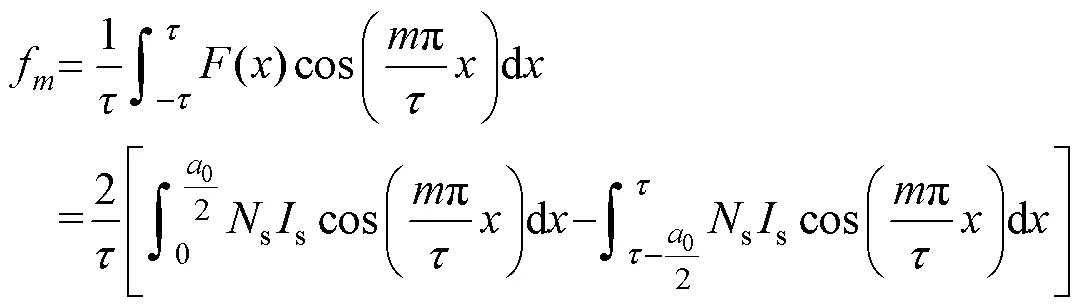
超導(dǎo)磁體中心軸坐標(biāo)為=0，依據(jù)式（1）得到其磁動(dòng)勢(shì)在方向分布的級(jí)數(shù)形式為

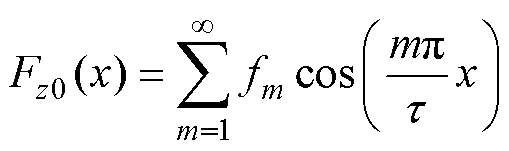
超導(dǎo)磁體磁動(dòng)勢(shì)在軸方向傅里葉系數(shù)f（= 1, 2, 3,…）為

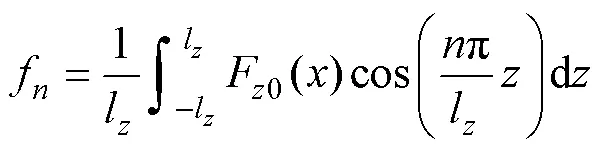
推出超導(dǎo)磁體磁動(dòng)勢(shì)在平面分布的級(jí)數(shù)為

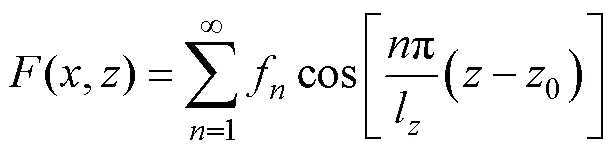
依據(jù)式（5），利用邊界條件[16]求解得到超導(dǎo)磁體在軸方向的磁感應(yīng)強(qiáng)度表達(dá)式為

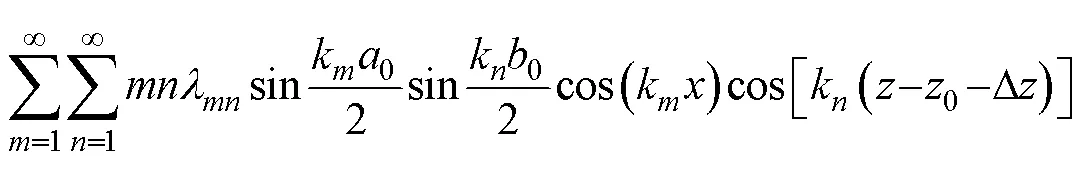
（6）

其中

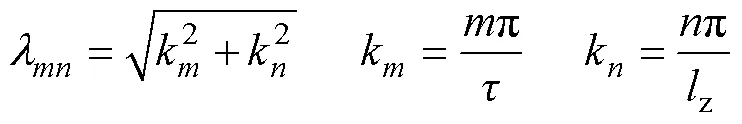
式中，0為超導(dǎo)磁體的高度。

2.2 懸浮線圈電流及其諧波磁場(chǎng)

圖4為各線圈在平面位置，原點(diǎn)為列車轉(zhuǎn)向架中心。超導(dǎo)磁體中心為（0,0,0），懸浮線圈中心為（1,1, 0），集電線圈中心為（2,2, 0）。1U、1B分別為懸浮線圈上線圈與下線圈中心軸坐標(biāo)，2U、2B分別為集電線圈上線圈與下線圈中心軸坐標(biāo)，2U、2B分別為集電線圈上線圈與下線圈高度，1為懸浮線圈高度。

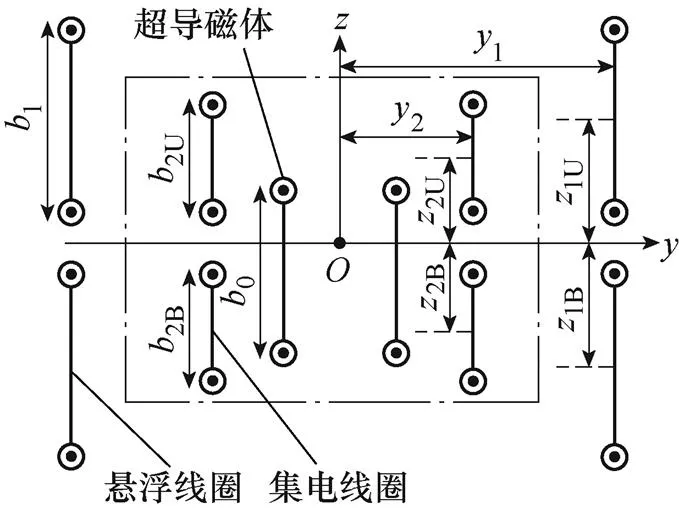
圖4 各線圈在yOz平面位置

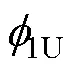
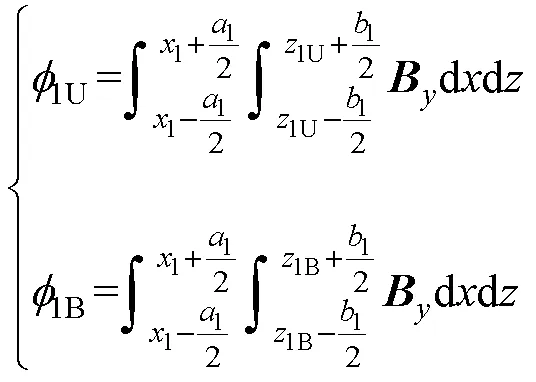
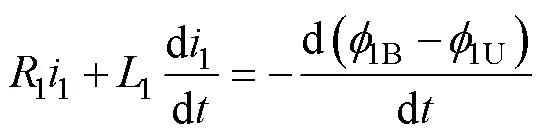
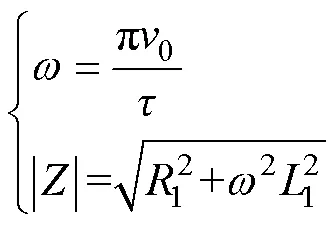
式中，1、1分別為懸浮線圈的電阻和電感；0為列車運(yùn)行速度；為懸浮線圈電流基波角頻率；|為懸浮線圈的阻抗的模值。

可解得懸浮線圈電流1為

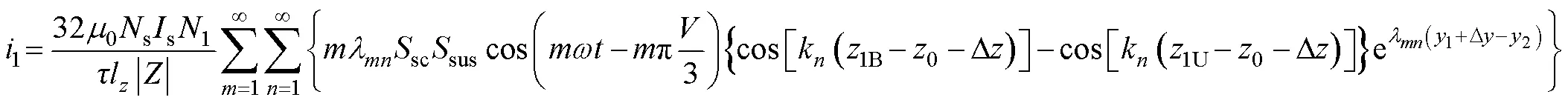
其中

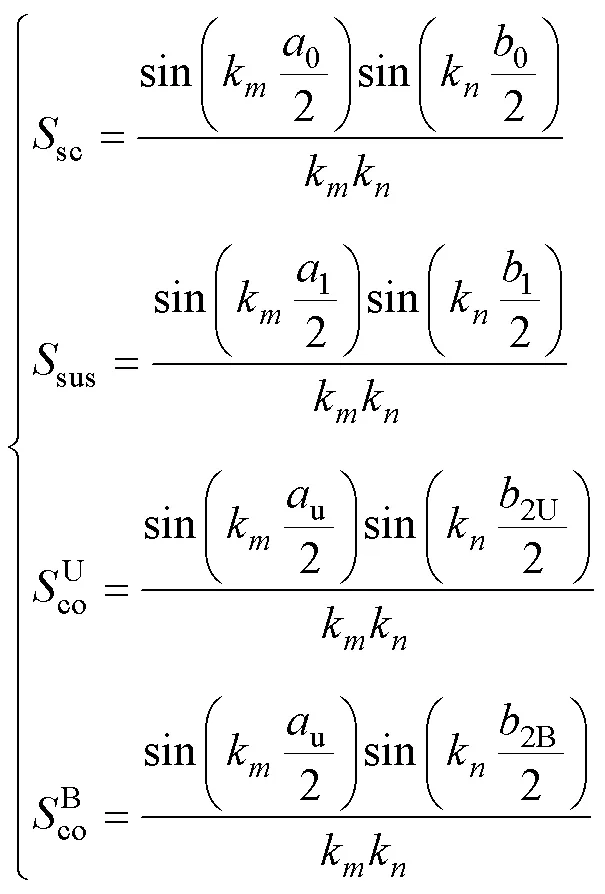
式中，為懸浮線圈標(biāo)號(hào)，如圖2所示；1為懸浮線圈匝數(shù)。

懸浮線圈電流的磁感應(yīng)強(qiáng)度推導(dǎo)過(guò)程和2.1節(jié)求解超導(dǎo)磁體磁感應(yīng)強(qiáng)度的方法類似，此處不再贅述。電動(dòng)懸浮系統(tǒng)直線發(fā)電機(jī)主要利用懸浮線圈電流的5次諧波磁場(chǎng)5i感應(yīng)發(fā)電[17]，懸浮線圈電流5次諧波磁場(chǎng)的磁感應(yīng)強(qiáng)度為

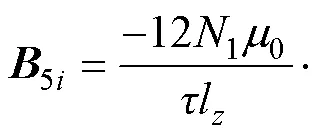
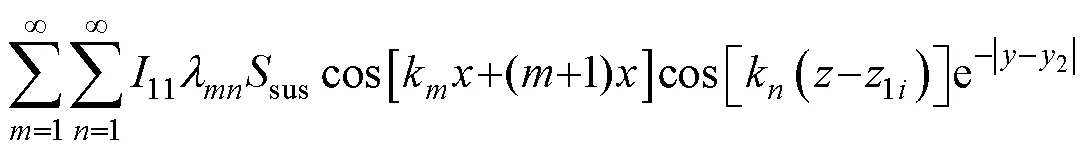
式中，當(dāng)=U時(shí)，5U為懸浮線圈上線圈的5次諧波磁場(chǎng)；當(dāng)=B時(shí)，5B為懸浮線圈下線圈的5次諧波磁場(chǎng)；11為懸浮線圈電流基波分量幅值。

懸浮線圈5次諧波磁場(chǎng)與集電線圈的交鏈磁通為

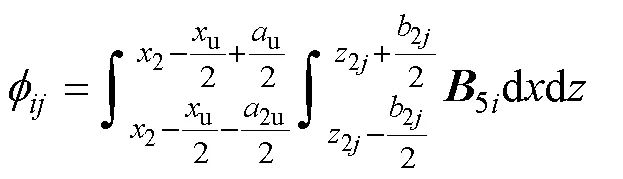
推導(dǎo)出集電線圈感應(yīng)電動(dòng)勢(shì)解析表達(dá)式[18-19]為

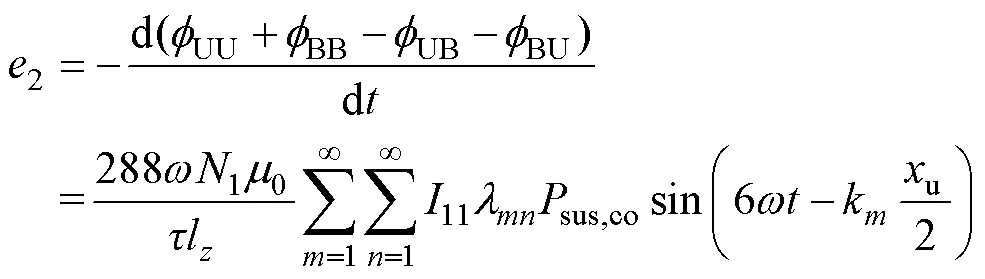
其中

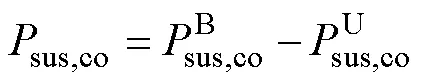
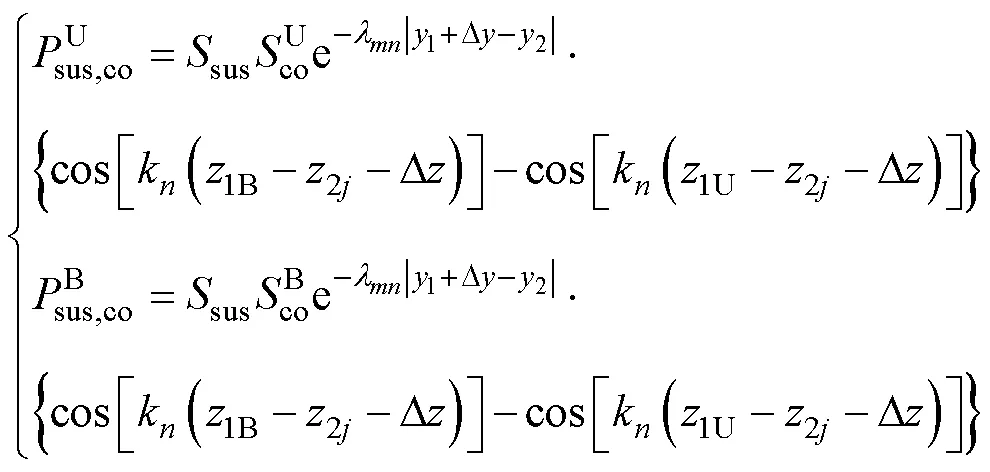
3 電磁特性分析與試驗(yàn)驗(yàn)證

3.1 電磁解析模型驗(yàn)證

以日本山梨試驗(yàn)線電動(dòng)懸浮系統(tǒng)直線發(fā)電機(jī)為研究對(duì)象，直線發(fā)電機(jī)主要參數(shù)[17]見(jiàn)表1。為驗(yàn)證電磁解析模型的有效性，將該文解析計(jì)算結(jié)果與有限元結(jié)果和實(shí)測(cè)數(shù)據(jù)[8, 10]進(jìn)行對(duì)比，解析結(jié)果與實(shí)測(cè)數(shù)據(jù)吻合較好，驗(yàn)證了解析模型的正確性。

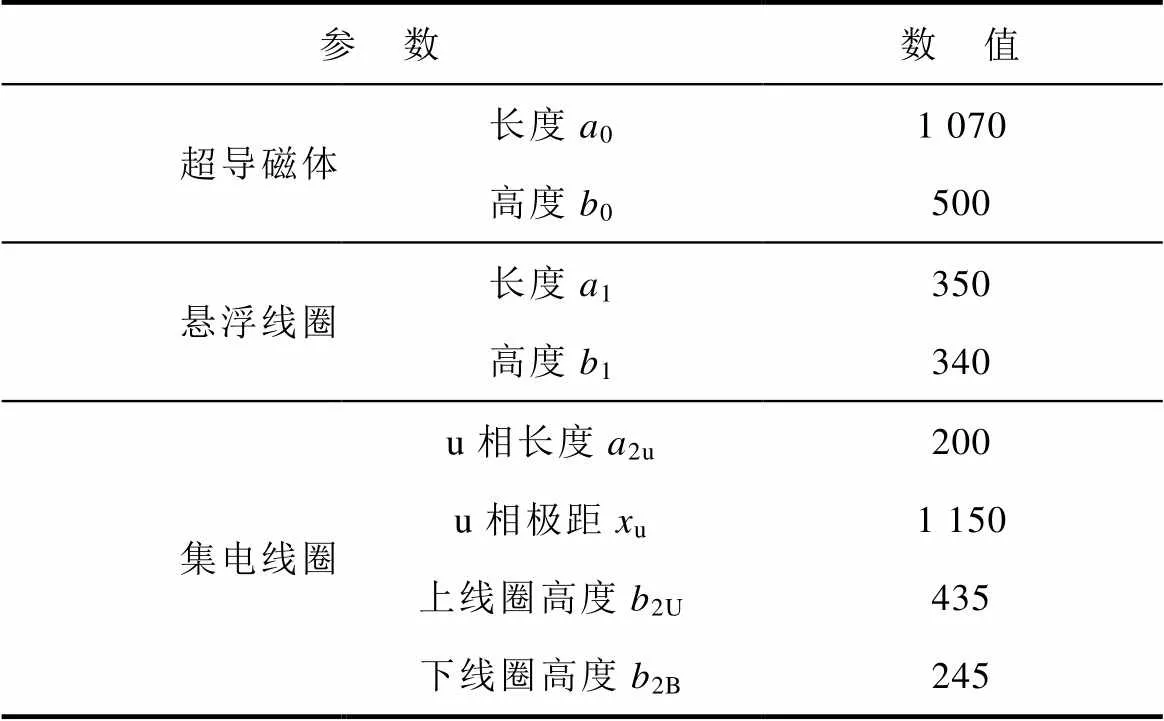
表1 直線發(fā)電機(jī)主要參數(shù)

解析值與有限元對(duì)比驗(yàn)證如圖5所示。圖5a為超導(dǎo)磁體磁感應(yīng)強(qiáng)度沿方向分布。可知，兩條曲線均呈馬鞍形，解析計(jì)算結(jié)果與有限元結(jié)果幾乎一致。圖5b為集電線圈感應(yīng)電動(dòng)勢(shì)解析值與有限元對(duì)比，相對(duì)誤差為2.6%，且曲線高度吻合，由此驗(yàn)證了解析模型的有效性。

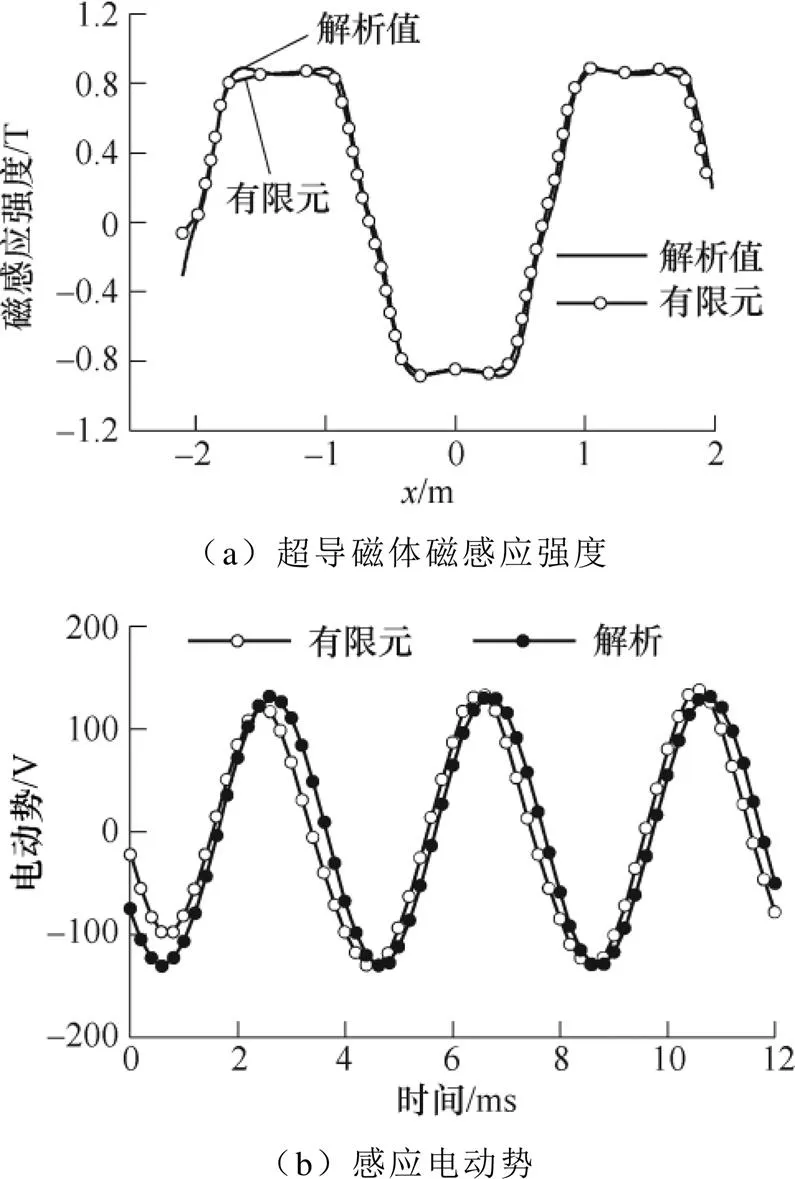
圖5 解析值與有限元對(duì)比驗(yàn)證

感應(yīng)電動(dòng)勢(shì)、功率對(duì)比驗(yàn)證如圖6所示。圖6a描述了集電線圈感應(yīng)電動(dòng)勢(shì)與速度的關(guān)系。可知，在100～500km/h區(qū)段，感應(yīng)電動(dòng)勢(shì)與速度近似呈線性關(guān)系。感應(yīng)電動(dòng)勢(shì)解析值與實(shí)測(cè)數(shù)據(jù)最大相對(duì)誤差為10.4%。圖6b為功率與速度的關(guān)系。可知，速度380km/h，達(dá)到目標(biāo)集電功率25kW。功率的解析值與實(shí)測(cè)數(shù)據(jù)最大相對(duì)誤差為8.7%，驗(yàn)證了電磁解析模型的正確性。誤差主要來(lái)源于試驗(yàn)設(shè)備中超導(dǎo)磁體外部杜瓦外殼表面的渦流會(huì)造成不可避免的測(cè)量誤差。

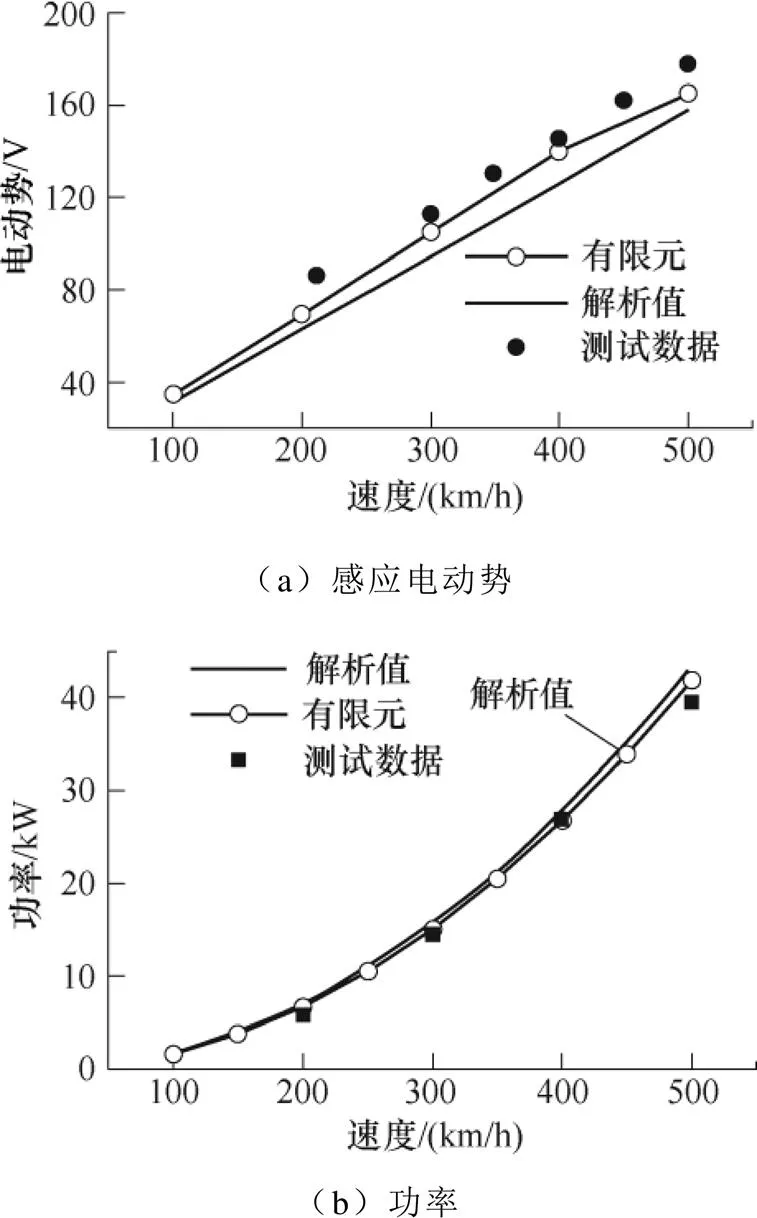
圖6 感應(yīng)電動(dòng)勢(shì)、功率對(duì)比驗(yàn)證

3.2 垂向位移和橫向位移下電磁特性

圖7為懸浮線圈電流5次諧波磁場(chǎng)與速度、偏移量的關(guān)系。速度大于100km/h，進(jìn)入飽和區(qū)段。這由于隨著速度升高，懸浮線圈中磁通變化率增大，懸浮線圈趨膚效應(yīng)的影響顯著，增大了懸浮線圈的交流阻抗，使磁感應(yīng)強(qiáng)度趨近飽和。

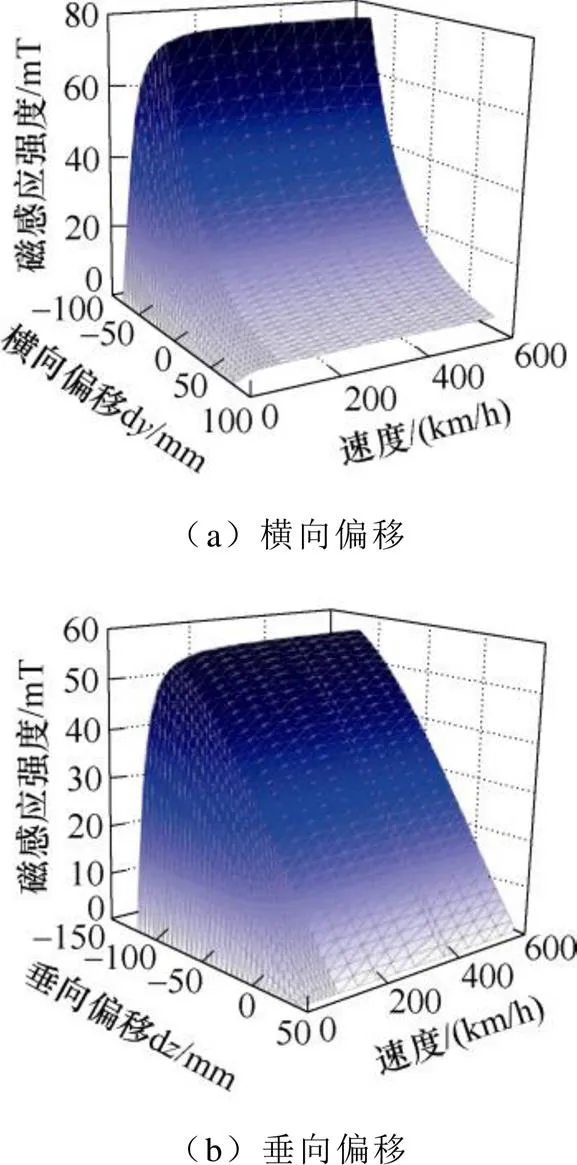
圖7 5次諧波磁場(chǎng)

圖8為功率和感應(yīng)電動(dòng)勢(shì)與垂向偏移的關(guān)系。可知，功率與感應(yīng)電動(dòng)勢(shì)隨垂向偏移增大，呈減小趨勢(shì)。當(dāng)D=-90mm，超導(dǎo)磁體底部與懸浮線圈底部正對(duì)，集電線圈與懸浮線圈電流交鏈磁通達(dá)到最大，此時(shí)功率和感應(yīng)電動(dòng)勢(shì)最大。D=40mm，超導(dǎo)磁體中心與懸浮線圈中心正對(duì)，集電線圈與懸浮線圈電流交鏈磁通為零，故功率和感應(yīng)電動(dòng)勢(shì)為零。

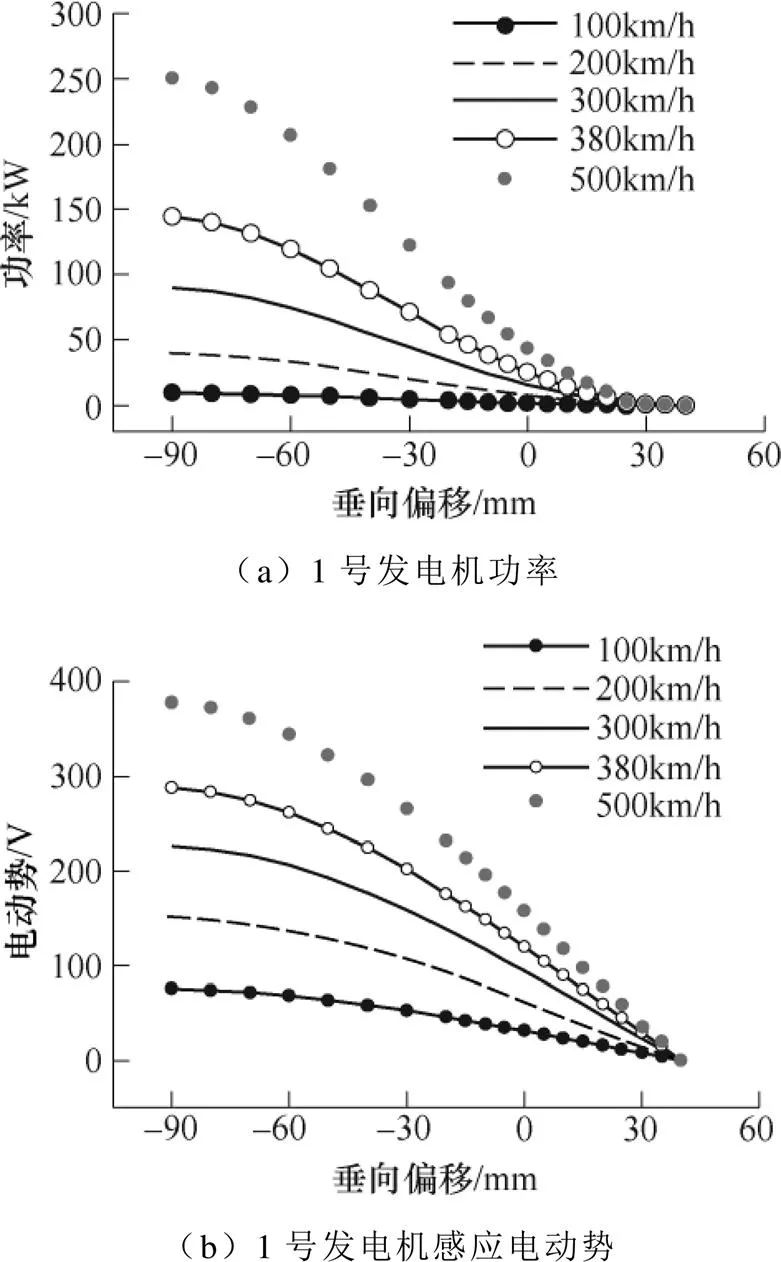
圖8 功率、感應(yīng)電動(dòng)勢(shì)與垂向偏移的關(guān)系

功率、感應(yīng)電動(dòng)勢(shì)與橫向位移的關(guān)系如圖9所示。圖9a為雙側(cè)發(fā)電機(jī)總功率與橫向偏移的關(guān)系。可知，雙側(cè)發(fā)電機(jī)總功率與橫向偏移量呈二次非線性關(guān)系，總功率隨橫向偏移量的絕對(duì)值增大，呈上升趨勢(shì)。圖9b為1號(hào)發(fā)電機(jī)感應(yīng)電動(dòng)勢(shì)，可知，感應(yīng)電動(dòng)勢(shì)隨橫向偏移呈遞減趨勢(shì)。原因是當(dāng)向軌道側(cè)發(fā)生橫向偏移時(shí)，懸浮線圈的諧波磁場(chǎng)與集電線圈的交鏈磁通量增大，從而感應(yīng)電動(dòng)勢(shì)上升。

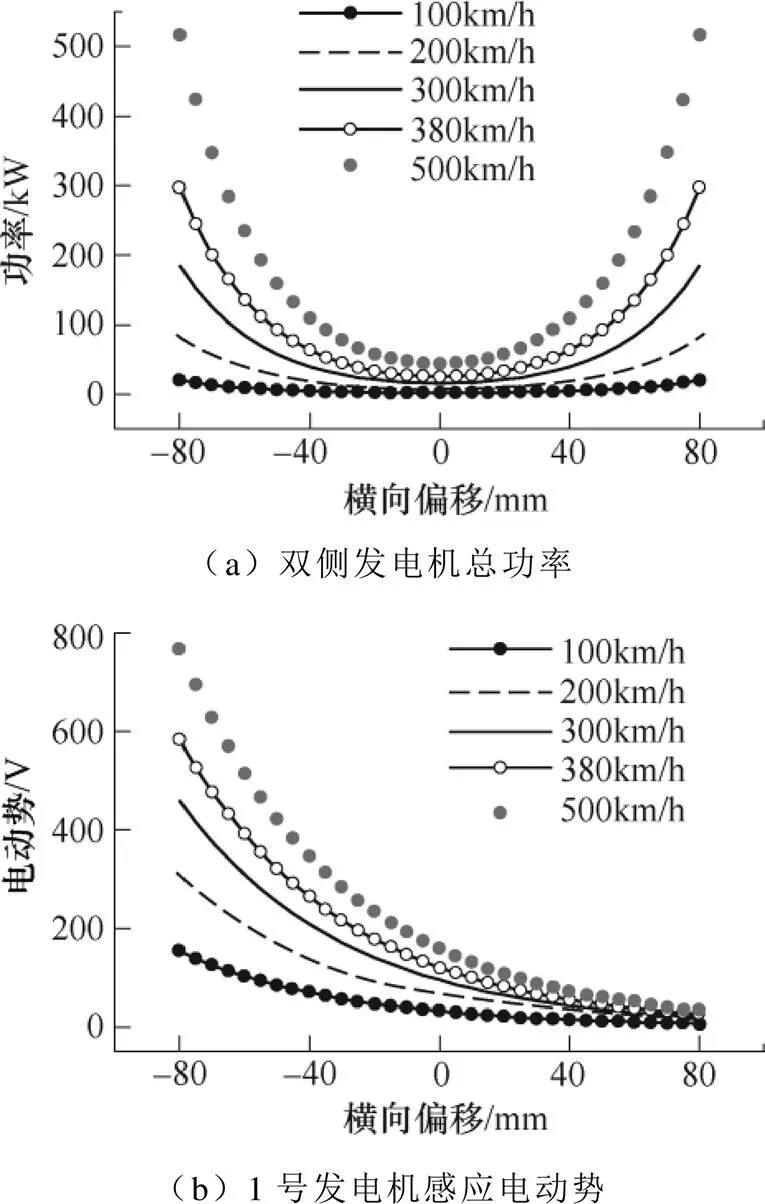
圖9 功率、感應(yīng)電動(dòng)勢(shì)與橫向位移的關(guān)系

4 結(jié)論

針對(duì)多工況下電動(dòng)懸浮系統(tǒng)直線發(fā)電機(jī)，建立了電磁解析模型，獲得了該工況下直線發(fā)電機(jī)的輸出特性，通過(guò)與山梨線試驗(yàn)數(shù)據(jù)對(duì)比，驗(yàn)證了模型有效性。計(jì)算結(jié)果表明，直線發(fā)電機(jī)功率與感應(yīng)電動(dòng)勢(shì)隨著垂向偏移的增大而減小。而兩側(cè)直線發(fā)電機(jī)總功率隨著橫向偏移的增大而增大。本文的工作在衡量高速磁懸浮列車的偏移工況對(duì)直線發(fā)電機(jī)的輸出特性的影響時(shí)具有指導(dǎo)意義，為高速磁懸浮系統(tǒng)直線發(fā)電機(jī)的設(shè)計(jì)和控制提供了相關(guān)理論基礎(chǔ)。

[1] 熊嘉陽(yáng), 沈志云. 中國(guó)高速鐵路的崛起和今后的發(fā)展[J]. 交通運(yùn)輸工程學(xué)報(bào), 2021, 21(5): 6-29.

Xiong Jiayang, Shen Zhiyun. Rise and future develop- ment of Chinese high-speed railway[J]. Journal of Traffic and Transportation Engineering, 2021, 21(5): 6-29.

[2] 呂剛. 直線電機(jī)在軌道交通中的應(yīng)用與關(guān)鍵技術(shù)綜述[J]. 中國(guó)電機(jī)工程學(xué)報(bào), 2020, 40(17): 5665-5675.

Lü Gang. Review of the application and key tech- nology in the linear motor for the rail transit[J]. Proceedings of the CSEE, 2020, 40(17): 5665-5675.

[3] 朱進(jìn)權(quán), 葛瓊璇, 孫鵬琨, 等. 高速磁懸浮列車在雙端供電模式下的電流控制策略[J]. 電工技術(shù)學(xué)報(bào), 2021, 36(23): 4937-4947.

Zhu Jinquan, Ge Qiongxuan, Sun Pengkun, et al. Current control strategy for high-speed maglev in the double feeding mode[J]. Transactions of China Electrotechnical Society, 2021, 36(23): 4937-4947.

[4] 郭亮, 盧琴芬, 葉云岳. 磁浮列車用直線發(fā)電機(jī)感應(yīng)電動(dòng)勢(shì)的分析計(jì)算[J]. 電工技術(shù)學(xué)報(bào), 2005, 20(11): 1-5.

Guo Liang, Lu Qinfen, Ye Yunyue. Analysis and calculation of the linear generator EMF in maglev[J]. Transactions of China Electrotechnical Society, 2005, 20(11): 1-5.

[5] Andriollo M, Martinelli C, Morini A, et al. Opti- mization of the on-board linear generator in EMS- MAGLEV trains[J]. IEEE Transactions on Magnetics, 1997, 33(5): 4224-4226.

[6] Kashiwagi T, Murai T, Yamamoto T, et al. Control of the output power and power factor in a converter of a linear generator for the maglev system[J]. IEEJ Transactions on Industry Applications, 2004, 124(10): 1029-1035.

[7] Murai T, Sakamoto Y, Hasegawa H. High power factor converter control by instantaneous single-phase current for a maglev system linear generator[C]// Power Conversion Conference-Nagoya, Nagoya, Japan, 2007: 1158-1163.

[8] Sakamoto Y, Murai T, Kashiwagi T, et al. The development of linear generator system combined with magnetic damping function[J]. IEEJ Transa- ctions on Industry Applications, 2006, 126(2): 192-198.

[9] Murai T, Hasegawa H, Fujiwara S. Improvement of inductive power collection in null-flux maglev system[J]. Electrical Engineering in Japan, 1998, 122(2): 48-60.

[10] Yamamoto T, Murai T, Hasegawa H, et al. Develop- ment of distributed-type linear generator with damping control[J]. Quarterly Report of RTRI, 2000, 41(2): 83-88.

[11] Murai T, Sakamoto Y. Sensor-less combined vertical and lateral magnetic damper by using linear gener- ator[J]. IEEJ Transactions on Industry Applications, 2006, 126(3): 269-275.

[12] 王一宇, 蔡堯, 宋旭亮, 等. 零磁通式電動(dòng)懸浮等效模擬系統(tǒng)的特性分析與實(shí)驗(yàn)[J]. 電工技術(shù)學(xué)報(bào), 2021, 36(8): 1628-1635.

Wang Yiyu, Cai Yao, Song Xuliang, et al. Charac- teristic analysis and experiment of the equivalent simulation system for null-flux electrodynamic suspension[J]. Transactions of China Electrotechnical Society, 2021, 36(8): 1628-1635.

[13] Lü Gang, Liu Yaqing, Zhou Tong, et al. Analysis of suspension and guidance system of EDS maglev based on a novel magnetomotive force model[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2022, 10(3): 2923-2933.

[14] Lü Gang, Liu Yaqing, Zhang Zhixuan, et al. Numerical analysis of the rotational magnetic springs for EDS maglev train[J]. CES Transactions on Elec- trical Machines and Systems, 2022, 6(1): 60-66.

[15] 章九鼎, 盧琴芬. 長(zhǎng)定子直線同步電機(jī)齒槽效應(yīng)的計(jì)算與影響[J]. 電工技術(shù)學(xué)報(bào), 2021, 36(5): 964-972, 1026.

Zhang Jiuding, Lu Qinfen. Calculation and influences of cogging effects in long-stator linear synchronous motor[J]. Transactions of China Electrotechnical Society, 2021, 36(5): 964-972, 1026.

[16] 秦偉, 范瑜, 徐洪澤, 等. 高溫超導(dǎo)運(yùn)動(dòng)磁場(chǎng)電磁Halbach初級(jí)結(jié)構(gòu)直線感應(yīng)磁懸浮電機(jī)[J]. 電工技術(shù)學(xué)報(bào), 2018, 33(23): 5427-5434.

Qin Wei, Fan Yu, Xu Hongze, et al. A linear induction maglev motor with HTS traveling magnetic electromagnetic halbach array[J]. Transactions of China Electrotechnical Society, 2018, 33(23): 5427- 5434.

[17] Murai T, Hasegawa H, Yamamoto T, et al. Active magnetic damper using linear generator[J]. IEEJ Transactions on Industry Applications, 1999, 119(11): 1371-1376.

[18] 李征, 邱書恒, 陳飛雪, 等. 基于預(yù)測(cè)算法的自由活塞內(nèi)燃直線發(fā)電機(jī)高效控制策略[J]. 電工技術(shù)學(xué)報(bào), 2022, 37(增刊1): 43-49.

Li Zheng, Qiu Shuheng, Chen Feixue, et al. Efficient control strategy based on predictive algorithm for free piston linear generator[J]. Transactions of China Electrotechnical Society, 2022, 37(S1): 43-49.

[19] 劉娜, 譚亦旻, 莫偉強(qiáng), 等. 基于模擬退火算法的Halbach直線發(fā)電機(jī)優(yōu)化設(shè)計(jì)[J]. 電工技術(shù)學(xué)報(bào), 2021, 36(6): 1210-1218.

Liu Na, Tan Yimin, Mo Weiqiang, et al. Optimization design of halbach linear generator with simulated annealing algorithm[J]. Transactions of China Elec- trotechnical Society, 2021, 36(6): 1210-1218.

Electromagnetic Characteristics Research of Electrodynamics Suspension Linear Generator under Multi-Condition

11211

（1. School of Electrical Engineering Beijing Jiaotong University Beijing 100044 China 2. CRSC Group Beijing 100044 China）

The Linear generator is the key equipment for contactless on-board power supply in the high-speed maglev system, and its output characteristics under multiple working conditions are the leading indicators of power generation capacity. The three-dimensional magnetic flux of the superconducting magnet is characterized by the space harmonic method, and the magnetomotive force distribution model of the linear generator is established. By analyzing the electromagnetic coupling relationship between the superconducting magnet and the suspension coil of the track-side wall, the expressions of the suspension coil current and the magnetic flux density of the suspension coil harmonic magnetic field are obtained. Further, the harmonic magnetic field of the suspension coil is used as the current collector coil to excite, and the numeric analytical expression for the induced electromotive force of the linear generator under multiple working conditions is deduced. Finally, compared with the test data of the Yamanashi Line in Japan, the accuracy of the magnetomotive force distribution model and the electromagnetic analytical model is verified. This work provides a theoretical basis for designing and controlling of linear generators for high-speed maglev systems.

High-speed maglev system, linear generator, electromagnetic analytical model, multi- condition, induced electromotive force

TM359.4

10.19595/j.cnki.1000-6753.tces.220464

國(guó)家自然科學(xué)基金資助項(xiàng)目（52077003, 51777009）。

2022-03-29

2022-06-28

呂 剛 男，1976年生，博士，教授，IET Fellow，研究方向?yàn)橹本€電機(jī)與磁懸浮技術(shù)。

E-mail: ganglv@bjtu.edu.cn（通信作者）

郭曦臨 男，1998年生，碩士研究生，研究方向?yàn)殡妱?dòng)懸浮系統(tǒng)直線發(fā)電機(jī)。

E-mail: 20121438@bjtu.edu.cn

（編輯 崔文靜）