城鎮智慧水務日用水量預測方法改進分析

孫小燕

(惠州市供水有限公司，廣東 惠州 516001)

1 概 述

隨著5G技術的發展，新基建應運而生，隨之而來的是智慧城市建設。作為智慧城市建設中重要一環的智慧水務，通過與新一代的5G技術與水務技術深度融合，用以實現水務系統的精確化、智能化管理，保證水務系統有效、科學地運行，從而極大地節省人力成本。在實際生活中，要采用信息技術對水務供給系統實施全過程監控，其中重要的一環是對城市用水量進行精確的預測[1-5]。

為此，許多學者采用不同方法對城市用水量進行了預測。李琳[6]以鄭州市為例，對城市用水量的預測方法進行總結，并采用灰色GM(1，1)模型及用水量定額法對鄭州市用水量進行了預測，結果顯示鄭州市用水量總體呈現出非線性增長趨勢。鄒廣宇[7]分析了城市用水量的影響因素，通過BP神經網絡建立預測動態用水量的預測模型，并通過沈陽市用水量對模型進行驗證，結果顯示該模型誤差較小。王圃[8]基于傳統灰色模型的局限性，在無偏灰色GM(1，1)的模型之上，提出一種加權組合模型，并使用該模型與無偏灰色GM(1，1)模型與非線性模型進行自由組合，通過該種組合模型對遂寧市用水量進行預測，研究顯示預測結果與實際效果吻合較好。嚴旭[9]采用GA遺傳算法對傳統BP神經網絡預測模型進行了改進，結合深圳市用水量特點，得出合適的輸入變量建立了預測模型，并對比深圳市的用水量驗證了該模型的可靠性。

上述研究通過建立預測模型或算法對城市用水量進行了預測，并給予一定的驗證。但實際上，用水量的變化特點具有一定的時變形和非線性，需要考慮到氣溫等諸多因素，而傳統的預測模型或算法往往很難體現這一點。因此，本文基于5G智慧水務技術，以H市自來水公司2020年的數據為研究對象，在考慮不同影響因素的條件下，對LR、SVR、BPNN這3種算法進行評估、改進，并對改進后的算法進行對比分析。

2 項目技術概況

工信部〔2020〕25 號文件提出，建立 NB-IoT(窄帶物聯網)、4G(含 LTECat1)和 5G 協同發展的移動物聯網綜合生態體系，在深化 4G 網絡覆蓋、加快5G 網絡建設的基礎上，以 NB-IoT 滿足大部分低速率場景需求，以 LTE-Cat1滿足中等速率物聯需求和話音需求，以 5G 技術滿足更高速率、低時延聯網需求。

在智慧水務項目實施過程中，很多應用場景基于 NB-IoT 實現物聯感知和智慧應用，NB-IoT 是 5G 的先行者，將成為 5G 關鍵技術之一。當前 NB-IoT 在 R15 版本能夠支持 NB-IoT 和 NR 空口共存，R16 版本支持 NB-IoT 接入 5G 核心網。根據 3GPP 自評估和中國獨立評估結果，NB-IoT 滿足 ITU mMTC 的要求，并已經通過 5G 候選提交，2020 年 7 月正式成為 ITU 5G 標準。

當前，業界已經認可 5G mMTC 的 LPWA 標準將基于 NB-IoT 平滑演進。因此，在當前智慧水務的網絡基礎設施建設中，必然會出現 NB-IoT 與 5G 網絡融合的應用搭配。5G 作為第 5 代蜂窩網絡，相比 4G 在峰值速率、網絡容量、連接密度等網絡性能方面有 10～100 倍的增強，其大寬帶、低時延、大連接的特性，將在智慧水務領域掀起一波新的物聯網應用浪潮。水務公司可以利用 5G 網絡實現全方位、立體化的智慧水務管理，特別是水務管網巡視、水廠無人值守視頻監控、VR 無人機安防等，而在遠程抄表等領域繼續采用 NB-IoT 平滑演進到 5G，從而兼顧更多更優的技術特征，豐富不同的應用場景。

3 研究方法

本文采用3種算法作為預測5G智慧水務用水量的基本預測研究算法，其中包括線性回歸算法(LR算法)、支持向量回歸算法(SVR算法)、神經網絡學習算法(BPNN算法)。

3.1 LR算法

線性回歸算法(LR)因其簡單基礎，是目前學界廣泛采用預測用水量的機器學習算法之一。對于用水量的預測，其線性回歸模型為：

Lθ(x)=θ0+θ1x1+θ2x2+…+θnxn

(1)

式中：Lθ(x)為預測用水量；x1，x2，…，xn為自變量影響因素；θ0為回歸常數；θ1，…，θn為權重系數。

3.2 SVR算法

用水量預測采用支持向量回歸算法(SVR)在支持向量機算法(SVM)的基礎上，更加適用于此類回歸分析。對于線性函數模型而言，通過在線性函數兩側設置間隔帶，對落入間隔帶內的樣本不計入損失，以此來最小化總損失和最大化間隔帶；而對于非線性函數則是通過核函數映射到線性空間之后，再進行回歸分析。采用SVR算法對用水量進行預測，假設間隔帶函數為：

f(x)=λTx+b

(2)

則利用該間隔帶函數可得到SVR求解的模型為：

(3)

式中：m為日用水量數據；αi為拉格朗日乘子；κ(x，xi)為核函數；yi為第i個樣本的實際日用水量；ε為允許誤差。

3.3 BPNN算法

神經網絡學習算法(BPNN)是目前最為常用的預測算法，由輸入層、隱層、輸出層構成，通過不同數量的神經元構成。采用BPNN算法對用水量進行預測時，需確定神經元數量和最大迭代次數，并通過神經網絡的輸出值與實際用水量的誤差，不斷更新連接權重。見圖1。

圖1 神經網絡學習算法(BPNN)結構圖

4 結果分析

4.1 用水量影響因素分析

本文以H市自來水公司2020年5月的用水量數據為例，將與方差相差較大的數據去除，并對該公司所在城市的用水量樣本數據進行分析。城市用水量受諸多因素影響，但一般受溫度、節假日、天氣等因素影響較大。本文以5月份日期為橫坐標，以用水量為左縱坐標，4種主要影響因素為右縱坐標，總結該公司所在城市5月份的用水量及影響因素，并繪制圖2。圖2中，0為工作日，1為節假日，天氣情況為量化后的效果，具體參考見表1。

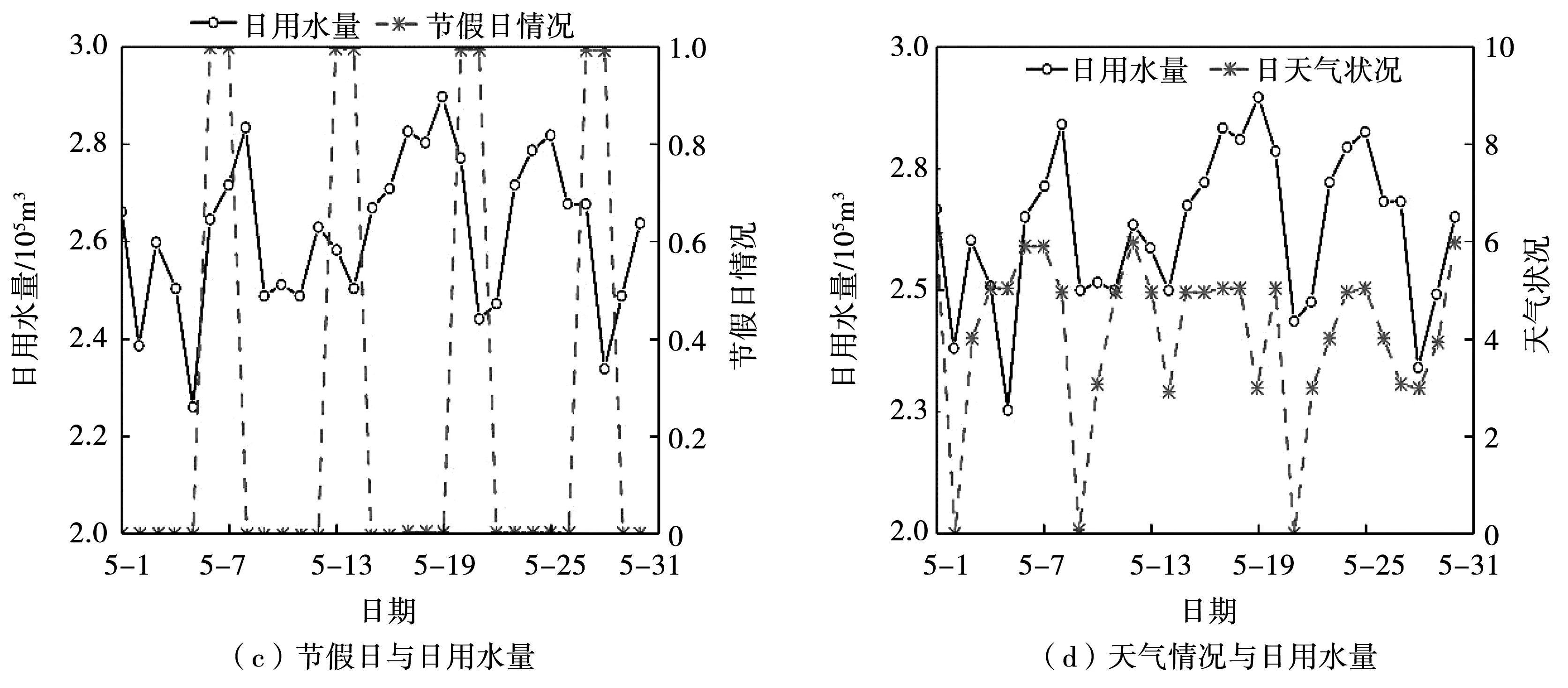
圖2 H市5月份用水量隨4種影響因素變化圖

表1 天氣情況量化數據表

圖2(a)和圖2(b)為最高氣溫與最低氣溫影響下的日用水量變化圖。從圖2(a)和圖2(b)中可以看出，隨著氣溫的升高，用水量也會隨之升高，溫度與用水量的變化呈現正相關。從圖2(c)可以看出，在工作日與節假日時，日用水量并無較大變化，其原因在于本次統計的用水量數據包含工業用水，由于工業用水量的存在，在節假日時整體用水量不會出現太大變化。圖2(d)為量化后的天氣情況影響下的日用水量變化圖，結合表1可以看出，天氣較好時日用水量有上升趨勢，但日用水量會隨著天氣轉陰轉雨而略有下降。

為了得出圖2中4種影響因素與日用水量的相關性，通過具體數據求取二者的相關系數ρ：

式中：ρ為相關系數；COV為協方差；X為影響因素因素；Y為日用水量。

通過式(4)得到不同影響因素與日用水量的相關系數，見表2。

表2 4種影響因素與日用水量的相關系數

從表2中可以看出，氣溫與日用水量的相關性最大；其次為天氣情況；節假日與日用水量的相關系數為負數，二者相關程度最低。

4.2 預測算法改進分析

分別采用LR、SVR、BPNN算法對H市自來水公司的數據進行預測。針對4個不同影響因素，通過建模與測試，對SVR算法的核函數選取RBF函數，并將函數中的參數C和g分別取值為3和0.016；對于BPNN算法則選取4個輸入層，20個隱層和1個輸出層。將此3種算法下輸出的預測結果對比真實用水量，并進行預測誤差的統計，3種算法的預測誤差見表3。

表3 3種算法下的預測誤差

可以看出，3種算法的預測誤差偏大。為此，本文對3種預測算法進行了改進。在相關預測中，考慮到通過前一日用水量對整體用水量預測的重要性，本文統計了H市自來水公司前一日用水量和前8 h用水量的數據，見圖3。

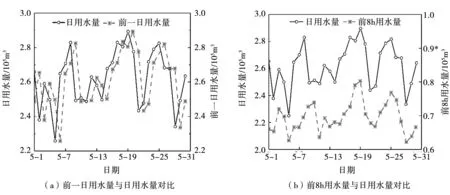
圖3 前一日及前8 h用水量與日用水量對比

為了得到其相關程度的高低，同樣采用式(4)計算其相關系數，見表4。

表4 前一日及前8h用水量與日用水量相關系數

通過上述計算分析可知，前一日用水量與前8h用水量均與日用水量相關程度較高，因此將此兩種影響因素加入到預測算法之中，以便獲得更小的誤差。為了降低預測誤差，對相關算法進行改進，對SVR算法的RBF核函數關鍵參數C和g分別設置為68和0.01；BPNN算法的輸入層神經元改為6個，隱層神經元及輸出層神經元數目均不變，分別設置50個測試集對相同的數據進行預測，計算相關算法的預測誤差，并與改進前算法的預測誤差進行對比，結果見圖4。

圖4 3種算法改進前后的預測誤差

從圖4中可以看出，對比改進前算法，在算法改進后誤差分布相對集中，整體誤差均處于0.1以下，說明改進后的算法具備更好的預測效果。對比不同的算法可以看出，隨著測試集的變化，BPNN算法波動程度較小，對于測試集內的預測效果最好；而SVR算法波動程度最大，穩定性較差。

由于氣溫對日用水量的相關程度最高，因此為了得到改進后算法在不同氣溫下的預測效果，本文對5月份進行了劃分，1-14日為a組，15-31日為b組，SVR和BPNN主要參數設置均不變，設置30個測試集對預測誤差進行測試，見圖5。

從圖5中可以看出，改進后的LR算法和BPNN算法在不同溫度下，預測誤差較為集中，說明在不同溫度下此二種算法依然可以保持較高的預測精度；但對于SVR算法，溫度的變化會引起其預測誤差隨之發生改變，溫度變高或者變低時，其預測精度會隨之下降，但這種情況隨著測試集的增加而減小。

圖5 改進后的3種算法在不同溫度下的預測誤差

5 結 論

本文基于5G智慧水務技術，以H市自來水公司2020年的數據為研究對象，在考慮溫度、節假日、天氣情況等影響因素的條件下，對LR、SVR、BPNN這3種算法進行評估、改進，并對改進后的算法誤差進行對比分析，結論如下：

1) 通過改進SVR、BPNN算法的主要參數，改進后算法的預測精度明顯較改進前有進一步提高。

2) LR、BPNN算法受測試集與溫度影響較小，但SVR算法受溫度影響較大，高溫或低溫均會減小其預測精度，通過增加測試集可以降低此類情況。建議在一般情況下，采用改進后LR、BPNN算法；在測試比例較大時，可以采用SVR算法進行用水量的預測。