基于源網荷儲協調優化的主動配電網網架規劃

郭曉澄

（廣東電網汕頭潮陽供電局，廣東 汕頭 515100）

0 引 言

配電網的協調控制是當前國內外專家學者的研究重點，分布式電源、電池儲能、可中斷負荷的研究較為成熟，已經廣泛應用于國內的電網規劃中。其中分布式電源具有節能環保的優點；電池儲能具有自適應調節和較好的儲放能力；可中斷負荷對電網的保護能力較好，安全性較高。在實際應用過程中，單一的配電網供電模式難以應對日益復雜的電網結構，常有經濟成本較高、運行方式單一、電網安全性不足的問題出現，基于此現象，充分遵循分解協調的設計原則，在設計過程中更加關注規劃結果的合理性和經濟性，采用樹形結構編碼的改進遺傳算法，并結合原對偶內點法對模型求解，17節點算例驗證了本文所提模型和算法的有效性，同時表明源網荷儲的協調優化對配電網架規劃結果和配電網負荷特性的改善作用[1]。

1 電池儲能出力時序動態建模

電池的運行周期直接影響儲存能力，單位運行周期內存越高，電池儲存能力越強。基于此，本文對電池儲能情況進行動態建模，電池儲能結構如圖1所示[2]。

根據圖1可知，電池儲能核心在并網側和電池側之間，并網側電池儲能出力為PBES，電池側根據儲能狀態不同分為P+和P-。由此可以通過分段函數代表動態建模的運行狀態為

式中：t為時間；Δt為電池狀態轉換的間隔時間；η+為電池充電效率；η-為電池放電效率；λ為1個循環周期。[3]將式（1）進行線性變換后得到

式中：Eba,i和Eba,t為電池儲能起始時間和儲滿時間的剩余電量。基于此動態建模運行電池5個周期后，計算得到電池最小電量系數平均值為0.2[4]。進而將電池儲放周期設為24 h，使用式（2）中的儲放方式，得到電池儲能出力時序動態建模如圖2所示。

2 建立規劃模型

為提升本次研究的科學性，本文根據目前配電網運行情況和主要故障類型，將規劃建模分為A、B、C模型，其中模型A主要研究配電網架規劃的故障問題，優化內容集中在配電網架上；模型B主要研究電池儲能的故障問題，優化內容集中在電池儲能和電池控制方面；模型C主要研究可中斷負荷和分布式電源的協調配合問題，優化內容集中在配電網運行方式上，A、B、C規劃建模的目標函數和約束條件如表1所示[5]。

3 總體求解流程

基于上述建模情況，本文選擇使用原對偶內點法作為主要算法，并結合樹形結構編碼的改進遺傳算法作為輔助算法，目的在于增加總體求解的自適應性，減少人為計算造成的誤差，并為建模數據增加群體搜索功能和外擴展功能，為求解后的算例分析打好數據基礎，同時樹形結構編碼的改進遺傳算法能夠將配電網架的結構組成部分進行樹狀結構編碼，從而降低解算難度[6]。

本文模型求解過程如下文所述。

（1）首先從電網數據信息庫中調取近5年的電網數據，包括配電網功率、電網負荷、電池儲能輸出等關鍵數據，并使用K-means聚類法，對調用出的數據進行數據分析和建立模型，其中建立模型應以應用場景為分類要素，并結合不同場景的電網作業時間、電網基礎數據，最終聚類成3個及以上代表場景（本文聚類成a1、a2、a3，與模型A、B、C對應）[7]。

（2）聚類代表場景后，應按照樹狀結構對配電網架進行編碼，編碼采取由上至下、由少至多的原則，最終以prim最小樹的個數規劃種群，不同種群應用不同規劃方案，最終對比優劣情況（本文規劃出b1、b2、b3，3個種群，與模型A、B、C對應）。

（3）確立代表場景和規劃種群后進入計算環節，計算順序為模型C→模型B→模型A，首先在a1場景中計算b1種群和模型C的運行數據，并按照順序更換場景和種群，從而得到模型C的最優配電網運行方式；再將模型C最優運行數據中的電網負荷數值和運行費用帶入模型B中，模型B繼續與場景和種群展開計算，獲取模型B最優配電網運行方式；最后將模型B的最優運行數據中的總負荷值進行方差計算，從而獲取耗能最小的電池放電方式和消耗費用[8]。

（4）上述計算完畢后應進行收斂性判斷，檢驗上述計算結果的正確性，若檢驗結果發現遺傳算法不收斂，應重新聚類代表場景。

（5）若收斂性判斷和遺傳算法均通過驗證，那么獲取的最優運行方式和最低消耗數值就是配電網架最優的規劃方案。

4 算例分析

4.1 算例概況

本文1∶1還原某市配電網進行算例分析，配電網規劃區節點為17個，具體節點數據如表2所示[9]。

表2 節點數據

通過表1節點數據可以得出，節點1的有功負荷、無功負荷均為0，所以判斷是上級電網交匯點，不納入分析；另外節點8、節點11、節點14這3處為中斷負荷節點，基于此，本次算計分析的分布式電源和電池儲能的設置情況如表3所示[10]。

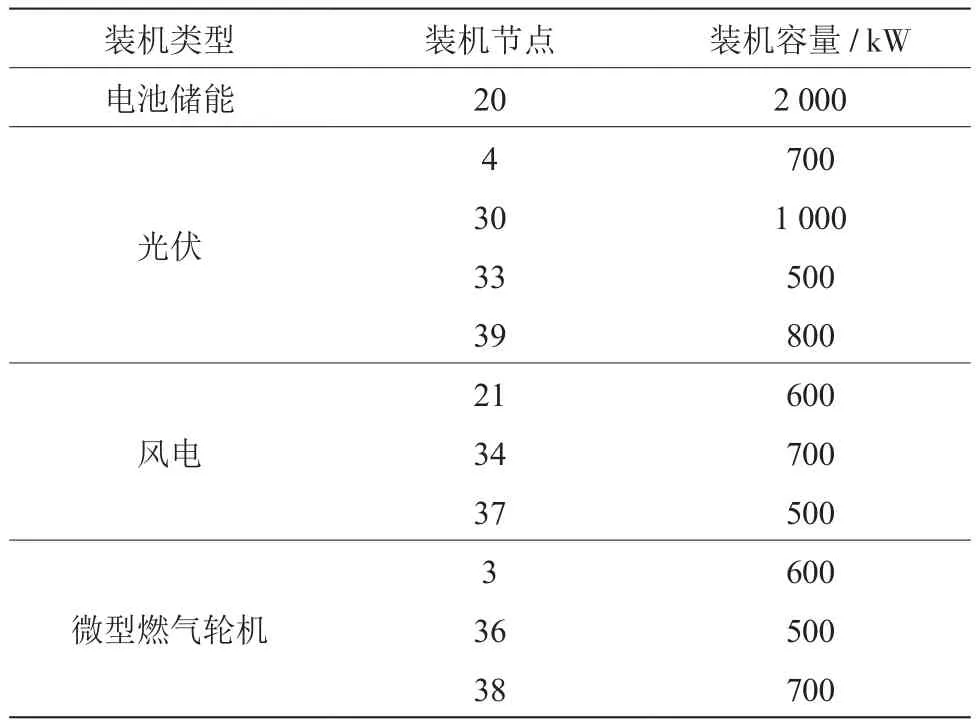
表3 電池儲能和分布式電源設置情況

通過表2、表3數據和近一年內電網維護成本、主動管理成本記錄，計算獲得分布式電源、光伏、風電、微型燃氣輪機3種裝機類型的成本消耗表如表4所示。

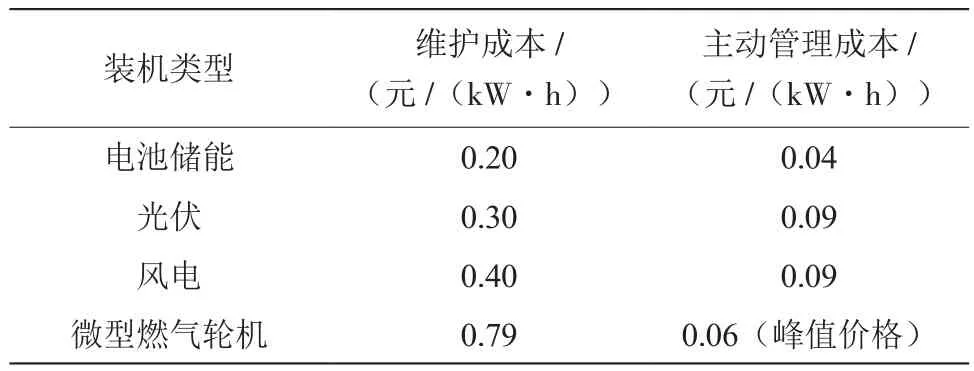
表4 電池儲能和分布式電源成本消耗表

通過表3、表4可以得出，電池儲能不僅單位裝機容量更高，消耗成本也低于光伏、風電、微型燃氣輪機3種分布式電源。

4.2 源網荷儲協調優化對配電網負荷特性的改善能力

為進一步研究源網荷儲協調優化對配電網負荷特性的改善能力，本文將最優配電網運行方式通過負荷曲線進行體現，初始負荷特性曲線如圖3所示，最優電池儲存能力如圖4所示[11]。

基于圖3和圖4，使用源網荷儲進行協調優化，優化后分為可中斷負荷和不可中斷負荷2種情況，其特性曲線如圖5、圖6所示。

根據圖5和圖6中峰值的變化情況和波動性減緩，能夠計算出優化前和優化后2種情況的負荷峰值和方差如表5所示。

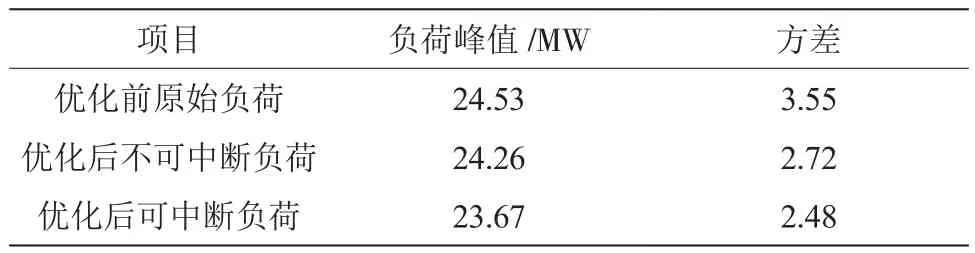
表5 優化前后負荷情況對比

通過表5可以得出，優化后不可中斷負荷對切除峰值效果較好、緩解負荷波動較差；優化后可中斷負荷對切除峰值效果較差、緩解負荷波動較好，原因在于電池具備分布式電源不具備的儲放功能，能夠對電網負荷進行自適應調整，在實際應用過程中，應根據實際情況協調使用2種優化方式，達到切除峰值和緩解負荷波動2種優化效果的統一體現[12]。

5 結 論

綜上所述，本文首先進行電池儲能出力時序動態建模，然后建立A、B、C3種規劃模型，說明總體求解流程，并以某市電廠實際數據為基礎進行算例分析，最終得到以下結論。

A、B、C 3種規劃模型能夠代表配電網網架規劃中的絕大部分情況，保證規劃結果是安全性和經濟性的最優方案。電池儲能相比于分布式電源具有裝機容量強、消耗成本低的優勢，并且具備切除峰值和緩解負荷波動2種功能，能夠提升配電網使用的穩定性。本文建立的電池儲能出力時序動態模型，能夠充分展現電池儲能的自適應性，并考慮了可中斷負荷的最大中斷時間和中斷比例會對規劃結果造成影響，與實際應用情況較為貼合。