串列非粘結柔性立管碰撞影響規律分析

陶 騰，張火明，陸萍藍，管衛兵

（1.中國計量大學a.浙江流量計量技術重點實驗室；b.工程訓練中心，杭州 310018；2.自然資源部第二海洋研究所，杭州 310012）

0 引 言

在深海油氣開發應用中，柔性立管是水下系泊系統不可缺少的組成部分，它聯接在海底井口和海上浮臺上，起著傳輸油氣的作用。在海洋工程已有的立管構型之中，柔性立管因其出色的流體動力學性能而廣泛用于深水油氣開發。其運動主要受到浮式平臺和海流等的影響，在極端海況下，深海系泊系統中相鄰的柔性立管因平臺運動、渦激振動等因素影響發生碰撞。如果碰撞過程中接觸力或碰撞的能量比較大，那么會在立管碰撞區域造成疲勞損傷，長期的疲勞損傷累積將對其運輸能力和浮動平臺的正常運行產生較大的影響。因此開展非粘結柔性立管的碰撞研究具有較大的工程意義。

到目前為止，對立管碰撞規律的研究主要基于兩個不同的出發點：一是避免碰撞，二是允許碰撞。從避碰的角度出發，主要研究立管干擾的設計準則。Kleran 等[1]研究了平臺下立管干擾的評價方法。下游立管為生產立管，上游立管分別為生產立管和鉆井立管，還考慮了渦激振動對立管干擾的影響。根據挪威深水工程允許碰撞的設計目標，對立管進行了一系列的實驗和數值模擬研究。Sagatun[2]采用數值實驗與系統辨識相結合的方法，對碰撞中隔水管的質量和能量進行了評估，得出碰撞中隔水管的長度為3.2%L～9.5%L（L為隔水管模型長度）。

在立管的碰撞研究中，單層立管研究得較多，而具有復合管道層結構的非粘結柔性立管的研究幾乎沒有。為研究海洋非粘結柔性立管的碰撞規律，采用有限元軟件ABAQUS開展FPSO海洋平臺下串列立管的碰撞研究，在考慮非粘結柔性立管骨架層和抗拉鎧裝層材料的非線性和管道層復雜的接觸的基礎上，考慮實際海洋立管的碰撞影響因素，選取碰撞速度、管間摩擦和管壁內壓三個影響因素作為單變量，研究對立管參與碰撞的區域沿碰撞方向的應力、應變和碰撞力等響應的影響作用。為避免非粘結柔性立管發生碰撞，選擇合適的碰撞速度、管間摩擦和管內壁壓參數，為立管的科學設計和安裝等提供一定的指導。

1 深海立管碰撞原理

深水立管碰撞是一個低速高能的瞬態沖擊過程，利用瞬態動力學基本方程可以分析碰撞過程，其方程為

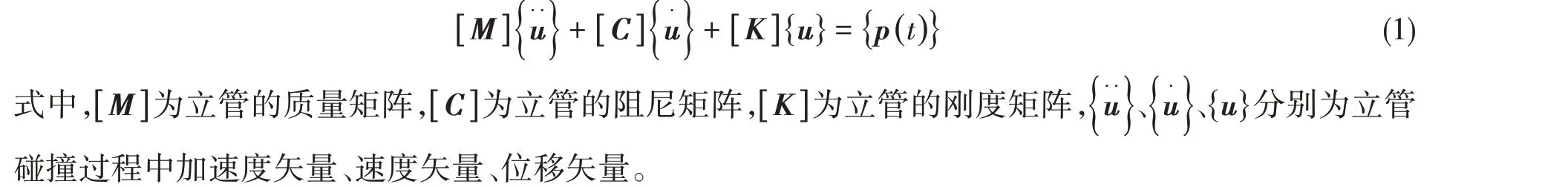
ABAQUS 中直接積分的顯式算法適用于響應時間短、時間增量較小的動態分析，例如結構碰撞、沖擊等場合。動態顯式算法的特征是將上一次計算的中間結果和遞歸算法用于下一次計算。收斂的穩定性條件是最大時間步長小于臨界時間步長，如公式（2）所示。

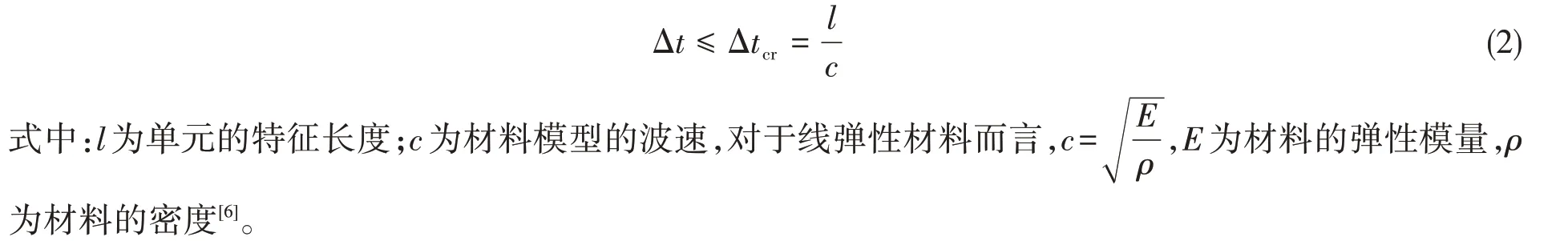
目前對于多層非粘結柔性立管的碰撞研究較少，基于其試驗成本較高，難以展開，因此采用數值計算的方法研究。首先就建模而言，非粘結柔性立管較單層立管具有多層復合管道結構，其中的骨架層、抗壓鎧裝層等管道材料為非線性的各向異性；其次非粘結柔性立管具有復雜的層間接觸，這導致非粘結柔性立管的建模非常復雜，同時復雜的結構和接觸模型將導致計算時間長且難以收斂。因此本文簡化立管的復雜結構模型，但考慮其材料的非線性和接觸，基于等效剛度理論[14]等將骨架層和抗壓鎧裝層等效為正交各異向層，等效后的骨架層和抗壓鎧裝層的材料參數如表1 所示，可以在ABAQUS 的材料屬性模塊賦予各層的材料參數，并且ABAQUS 的相互作用模塊可以模擬其層間的復雜接觸。

表1 等效正交層材料參數Tab.1 Material parameters of equivalent orthogonal layer

2 立管碰撞數值模型

在深水立管碰撞過程中，實際只有一小部分區域參與了碰撞。碰撞區域長度與柔性管的抗彎剛度、等效外徑和壁厚有關。如公式（3）～（4）所示。計算得到軸向0.12 m 為碰撞區域長度，且立管局部碰撞研究大多以裸管為主，因此選取兩根長度為1 m 的裸管作為研究對象。非粘結柔性立管參數[3]如[3]表2 所示。考慮柔性立管管內的輸油特性，確定影響立管碰撞的三個單因素的范圍，其中內護套層中存在0 MPa、1 MPa、2 MPa 三種內壁壁壓。立管管間摩擦系數存在0、0.05、0.1 三種。立管碰撞的相對速度為1-3 m/s,計算時設置1 m/s，2 m/s和3 m/s三種。

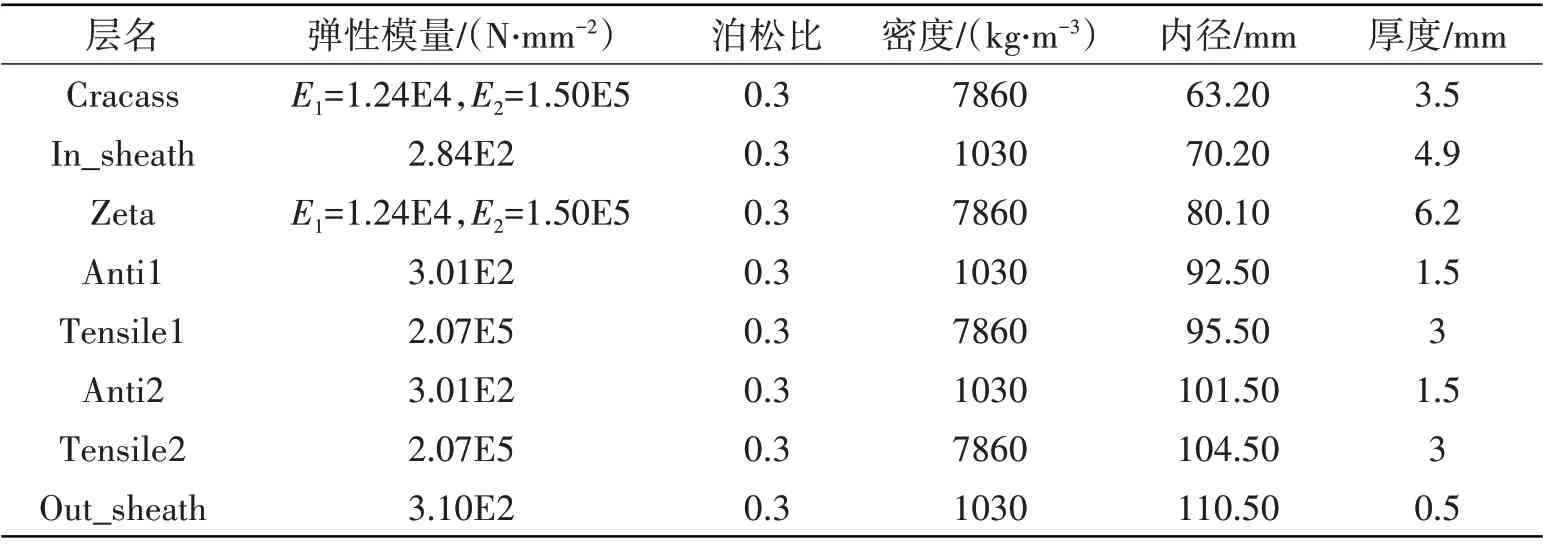
表2 非粘結柔性立管管層材料參數Tab.2 Material parameters of non-bonded flexible riser pipe layer

碰撞區域長度計算公式為[4]

式中，Li為立管碰撞參與長度，EIi為管彎曲剛度，Kc為觸剛度，D1、D2為兩立管的等效外徑，t1、t2表示兩立管的等效壁厚。

在ABAQUS 中建立碰撞模型后，需要進行立管的碰撞分析設置，主要包括分析步的設置、層間的接觸和摩擦等的設定、立管的約束和荷載的定義以及網格的劃分和沙漏問題的控制，沙漏現象的出現是采用非線性縮減積分的SCR4單元劃分網格，而采用縮減積分是給立管實際參與碰撞過程的接觸區域局部加密，能更精確地得到碰撞過程的數據。串列非粘結柔性立管碰撞模型如圖1 所示，部分設置在ABAQUS中如下所述。

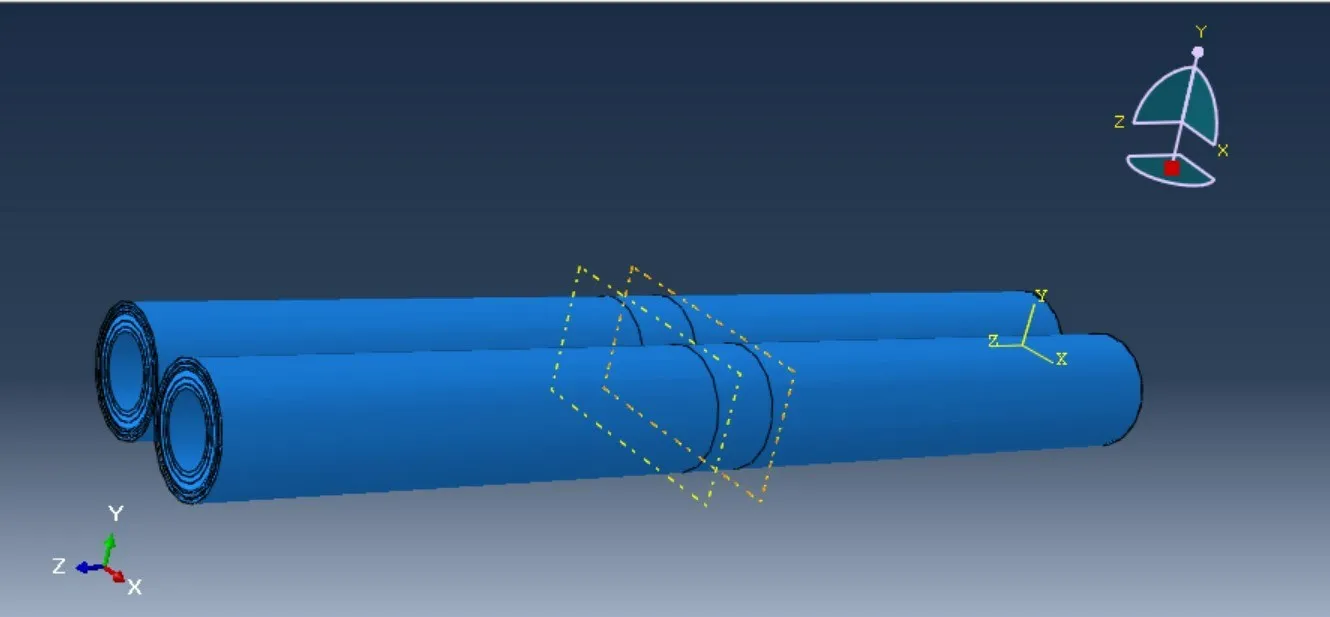
圖1 串列非粘結柔性立管碰撞模型Fig.1 Crash model of tandem unbonded flexible riser

（1）分析步的設置：分析步時長為0.1 s，最大時間增量為1E-3 s。

（2）相互作用模設置：立管層間的接觸屬性為切向屬性中選擇定義摩擦系數，法向屬性中選擇“硬”接觸；接觸對則為串列立管外護套層分割的碰撞區域，類型是表面與節點的接觸，以及建立立管兩端的運動耦合來實現串列柔性管之間的接觸屬性的作用，也為下一步的約束和載荷設置奠定基礎。

（3）約束條件設置：將串列布置的一對立管中下游立管定義為被撞管，兩端約束設置為完全固定，上游立管為運動管,其約束為僅沿垂直立管軸向方向的平移運動。在設置約束及載荷前，先在兩立管的兩端中心分別建立參考點，將其與所在端平面的點或面組合建立運動耦合關系[5]，通過運動耦合關系實現立管的端面邊界約束。上游運動管的速度通過設置預定義的速度場來實現。最后，對兩個立管的內外套層內壁施加壓強荷載。

3 仿真驗證與分析

碰撞過程中立管的能量-時間曲線圖如圖2 所示。碰撞過程中系統總的內能（ALLIE）包括偽變形能（ALLAE）、動能（ALLKE）以及碰撞過程中消耗的能量。在能量時程曲線圖中，偽變形能的數值幾乎為0，按照碰撞計算的規定，當偽變形能與內能之比小于10%時，表明沙漏控制效果好，同時可以說明計算結果是準確可靠的。

圖2 沙漏控制驗證Fig.2 Hourglass control verification

根據Mott Macdonald 等關于立管碰撞的研究中所選取的碰撞速度為0～3.1 m/s,本算例中碰撞速度單因素依次設為1 m/s、2 m/s、3 m/s。當碰撞速度為3 m/s時。碰撞計算完成后被撞管的應力和應變云圖如圖3～4 所示。可以看出碰撞后應力高度集中在立管的碰撞區域中心，這符合我們熟知的碰撞規律。在立管相互碰撞的過程中，沖擊能從中間碰撞接觸區域開始向四周區域擴散，從而發生多次碰撞行為，碰撞后立管應力和應變等整體將顯示一個漸進的形狀，中心大、兩端較小的分布。

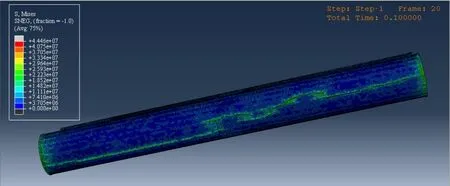
圖3 被撞管的應力云圖Fig.3 Stress cloud diagram of the collided pipe

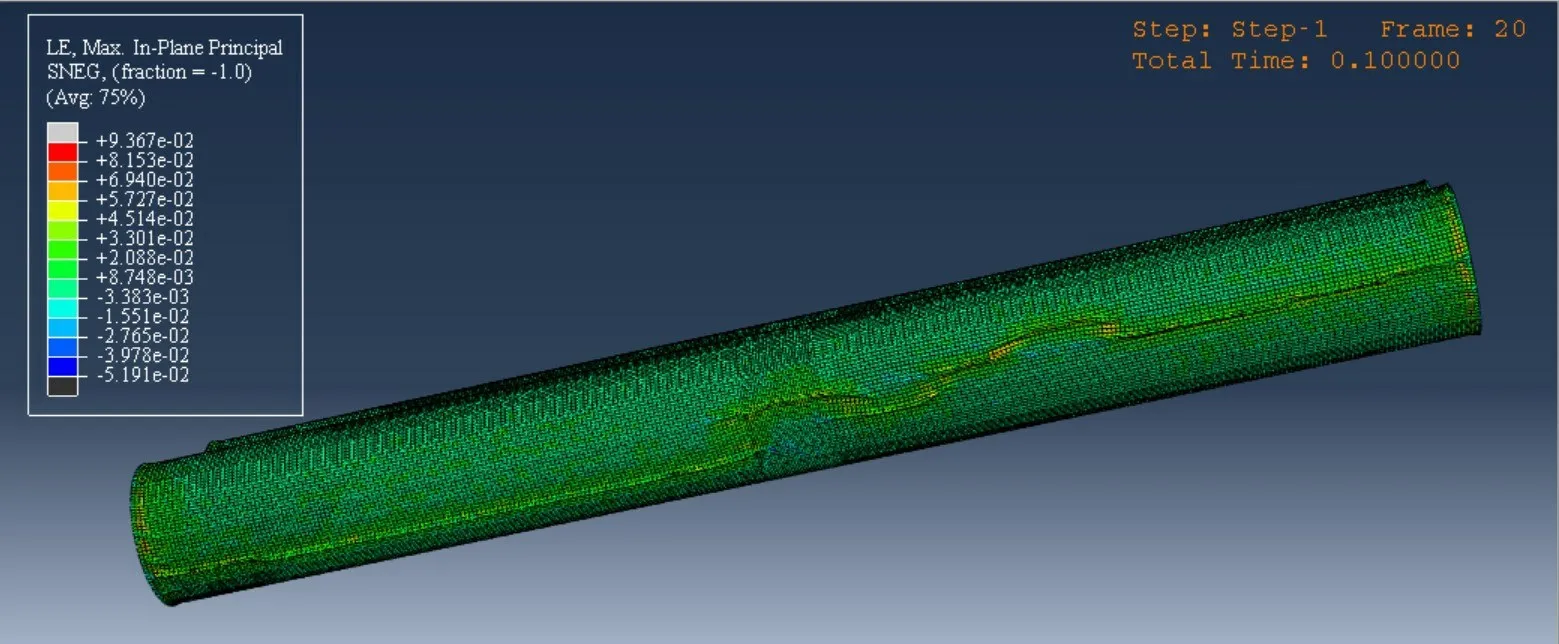
圖4 被撞管的應變云圖Fig.4 Strain cloud diagram of the collided tube

3.1 上游運動管速度對下游被撞管碰撞的影響

單層運動管的初始速度范圍為1～3 m/s[8]，本算例取1 m/s、2 m/s 和3 m/s 共計3 個碰撞速度值點。其他兩個單一因素保持管內壁壓初始為1 MPa，摩擦系數為0.1 不變。非粘結柔性運動管的初始碰撞速度范圍和取值與單層立管一樣。其他兩個單一因素與單層立管設置相同，計算結果顯示在圖5～7中。

圖5 單層立管不同碰撞速度的應變Fig.5 Strain of a single-layer riser at different collision velocities

圖6 單層立管不同碰撞速度的應力Fig.6 Stress of a single-layer riser at different collision velocities

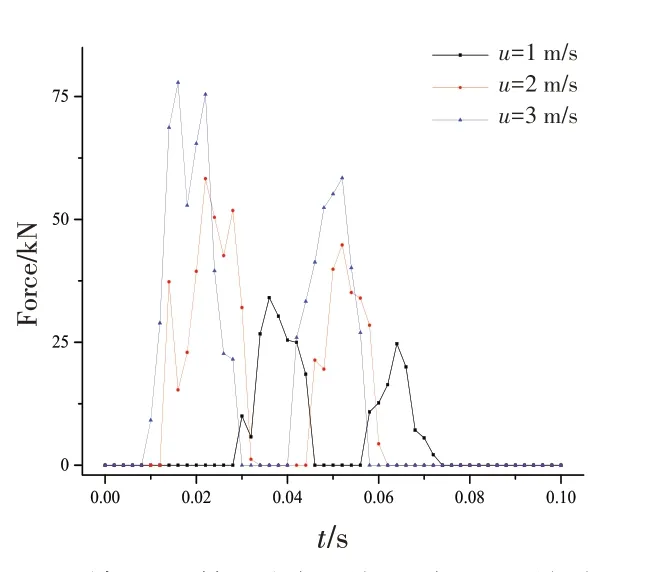
圖7 單層立管不同碰撞速度的碰撞力Fig.7 Collision force of single-layer riser with different collision speeds

圖8 非粘結柔性立管不同碰撞速度下的應變Fig.8 Strain of an eight-layer riser at different collision speeds

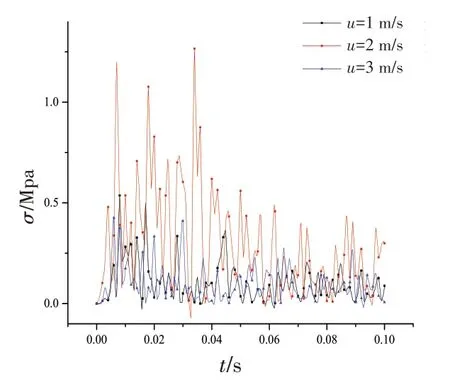
圖9 非粘結柔性立管不同碰撞速度下的應力Fig.9 Stresses of an eight-layer riser at different collision speeds

一般而言，碰撞速度對立管碰撞的影響為：隨著碰撞速度的增加，高應力區域越來越集中，同時應變和碰撞力也隨碰撞速度的增加而變大。單層立管碰撞結果如圖5～7所示，在時間大約在0～0.03 s內發生第一次碰撞行為，隨著碰撞速度增加，下游被撞管的對數應變、應力和碰撞力的大小都隨著碰撞速度的增加而增加，兩次速度改變下，最大應力分別增加了8 MPa、60 MPa，表明速度增加到一定值后，速度對立管碰撞應力的影響逐漸減弱。立管在速度為3 m/s時，接觸力和應力達到最大，分別為78 kN和212 MPa，小于立管的屈服應力552 MPa，所以再未發生塑性應變。與楊尊儒等［7］的研究中碰撞速度對立管碰撞影響結果相似[6]；從圖8～10所示的多層非粘結柔性立管碰撞可以看出：八層簡化立管在第一次碰撞過程中，隨著碰撞速度大小的逐漸增加，下游被撞管應力和接觸力的幅值都隨碰撞速度的增加而增加，且速度為3 m/s 時的接觸力最大，分別為78 kN 和212 MPa，小于屈服應力552 MPa，同理在立管碰撞過程中未發生塑性應變。

同時從圖10非粘結柔性立管碰撞過程碰撞力結果可知，非粘結柔性立管在不同碰撞速度下發生了多次碰撞，且第一次碰撞過程中的碰撞力遠遠大于其他幾次碰撞過程，碰撞速度為3 m/s時，第一次碰撞過程的最大碰撞力為240 N，遠大于第二次的19 N，因此重點分析第一次碰撞過程。第一次碰撞時間發生在0～0.01 s內,期間非粘結柔性立管的應變和應力隨碰撞速度的增加呈現先增加后減小的趨勢,碰撞速度為2 m/s時應力最大為1.20 MPa,遠小于其屈服應力21 MPa,因此非粘結柔性立管在碰撞過程中未發生塑性變形。

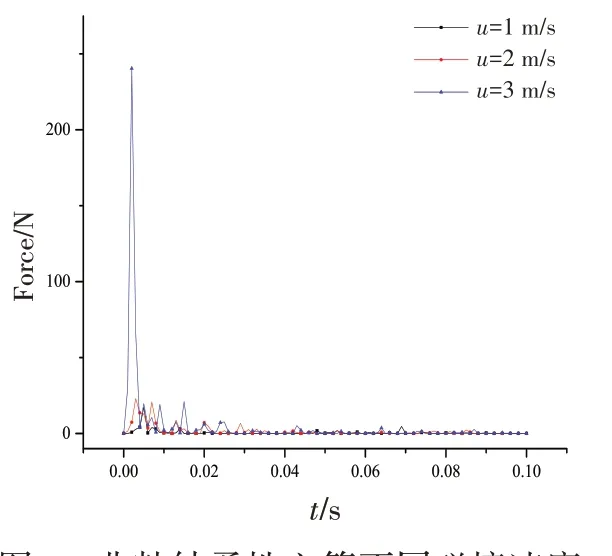
圖10 非粘結柔性立管不同碰撞速度下的碰撞力Fig.10 Collision force of eight-layer riser at different collision speeds

3.2 有無摩擦對碰撞結果的影響

單層運動管的管間初始摩擦系數區間為0～0.1[8-9，12]，取0、0.05和0.1共計3個摩擦系數取值點。而其他兩個單因素：內壓1 MPa，碰撞速度為2 m/s保持不變，計算結果如圖11～13所示；八層非粘結柔性運動管的初始摩擦系數區間和取值相同，而其他兩個單因素同上保持不變，計算結果如圖14～16所示。

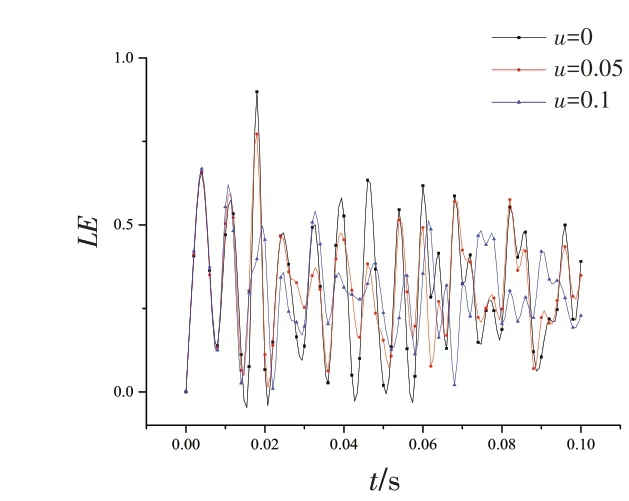
圖11 單層立管不同摩擦下的應變Fig.11 Strain of a single-layer riser under different frictions

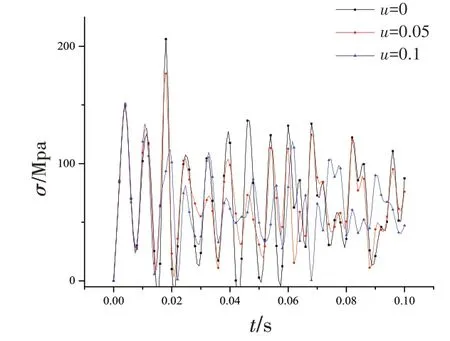
圖12 單層立管不同摩擦下的應力Fig.12 Stress of a single-layer riser under different frictions

圖13 單層立管不同摩擦下的碰撞力Fig.13 Collision force of a single-layer riser under different frictions

從圖11～13可以看到，單層管在第一次碰撞過程中，隨著管間摩擦系數的增加，對被撞管的應變、應力和接觸力幾乎無影響。

由八層非粘結柔性立管不同摩擦下碰撞過程的應變、應力和碰撞力時程曲線圖14～16可知，管間有無摩擦對立管碰撞的應力有較大的影響，隨著碰撞管層材料的摩擦系數增加，碰撞過程中立管的接觸力呈先增加后減小的趨勢，在摩擦系數為0.05 時，碰撞過程中的碰撞力最大，同時隨著摩擦系數的增加，立管碰撞區域的對數應力和對數應變隨之先減小后增加，在無摩擦條件下，非粘結柔性立管碰撞過程的應力最大，達到3.1 MPa，遠小于屈服應力，未發生塑性變形。

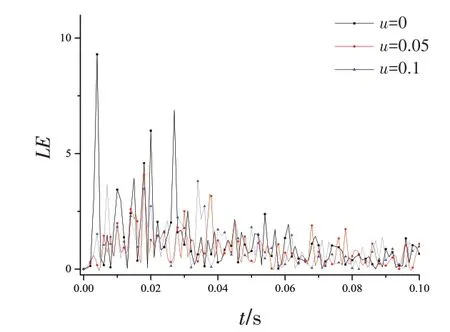
圖14 非粘結柔性立管不同摩擦下的應變Fig.14 Strain of non-bonded flexible riser under different frictions

圖15 非粘結柔性立管不同摩擦下的應力Fig.15 Stress of non-bonded flexible riser under different frictions

圖16 非粘結柔性立管不同摩擦下的碰撞力Fig.16 Collision force of non-bonded flexible riser under different frictions

3.3 不同管壁內壓對碰撞結果的影響

單層運動管的初始內壓區間為0～2 MPa[10-11，13]，取0 MPa、1 MPa、2 MPa 共計3 個內壓值，而其他兩個因素保持不變：摩擦系數0.1，碰撞速度為2 m/s；八層運動管的初始內壓區間和取值同上。計算結果如圖17～22所示。

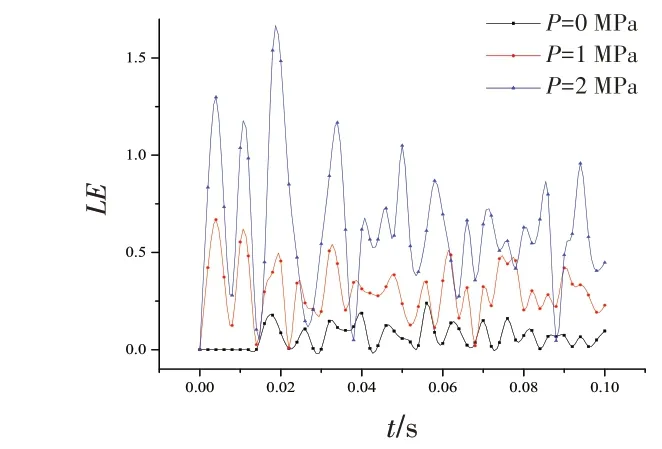
圖17 單層立管不同內壓下的應變Fig.17 Strain of a single-layer riser under different internal pressures

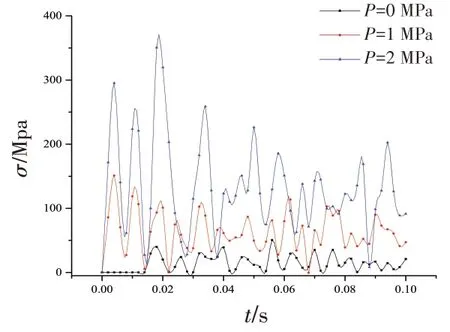
圖18 單層立管不同內壓下的應力Fig.18 Stress of a single-layer riser under different internal pressures

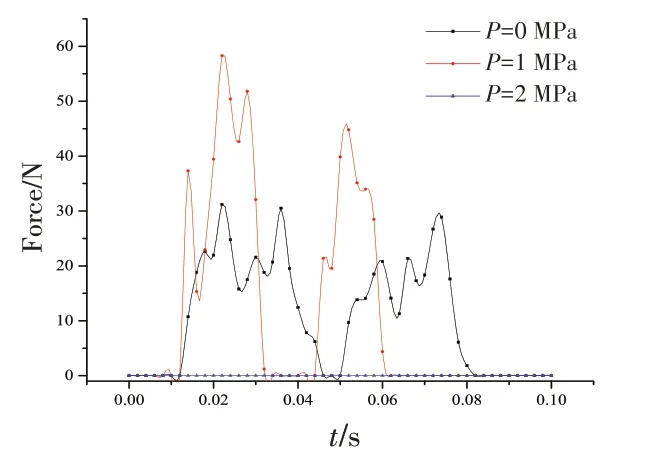
圖19 單層立管不同內壓下的碰撞力Fig.19 Collision force of a single-layer riser under different internal pressures

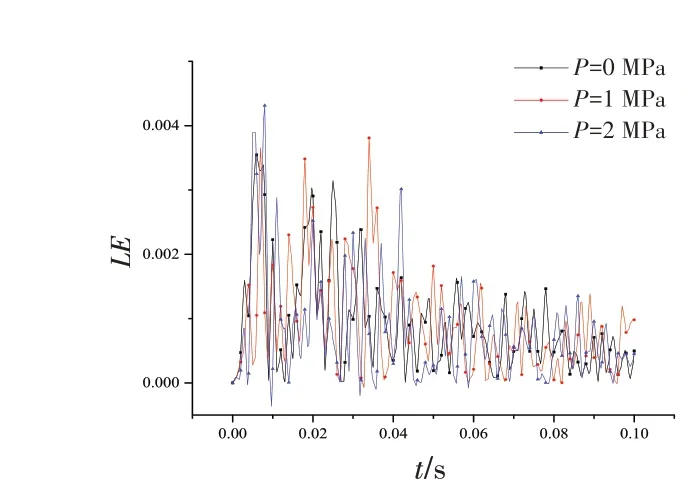
圖20 非粘結柔性立管不同內壓下的應變Fig.20 Strain of non-bonded flexible riser under different internal pressures

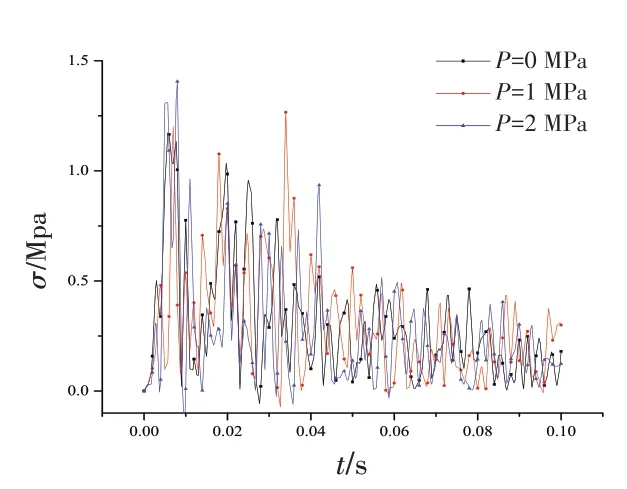
圖21 非粘結柔性立管不同內壓下的應力Fig.21 Stress of non-bonded flexible riser under different internal pressures

圖22 非粘結柔性立管不同內壓下的碰撞力Fig.22 Collision force of non-bonded flexible riser under different internal pressures

已有的內壓對于立管碰撞的影響：一定的管內內壓值使得立管在遭受外部撞擊時內部有一定的抵抗力，海洋立管碰撞產生的凹陷形變隨著內壓的增大而不斷減小，使得碰撞沖擊能量更多地用來導致立管的總體破壞而不是局部破壞；隨著海洋立管內壓的持續增加，內壓對立管凹陷形變的影響越來越小，當內壓達到某一值時，立管抵抗凹陷形變的能力不再增加。這就導致了立管的碰撞應力出現了先下降后上升的變化規律。

由單層立管不同管壁內壓下的碰撞曲線圖17～19 可知，隨著管壁內壓的增加，被撞立管的應變、應力和接觸力的幅值都隨著管壁內壓呈先增加后減小的趨勢。當壁壓為2 MPa 時，立管的最大碰撞力的數量級在1E-4 Ν，遠小于壁壓為0、1 MPa時的接觸力，其原因是內壓的存在導致立管徑向作用力減小。管內的壓強能降低立管碰撞時的應變，管內壁壓為2 MPa時的最大應力為365 MPa,小于屈服應力552 MPa。

八層非粘結柔性立管不同管壁內壓下的碰撞曲線如圖20～22 所示，可以看到隨著管壁內壓的增加，被撞立管接觸力的幅值都隨著管壁內壓呈先減小后增加的趨勢，同時非粘結柔性立管碰撞的應力和應變隨管內壁壓的增加而逐漸增加，且增加的幅度隨管壓的增加而逐漸增加，在內壓為2 MPa時其最大應力為1.4 MPa，仍小于屈服應力，未發生塑性應變。多層立管的壁壓影響下的響應規律可能與多層非粘結柔性立管復雜的層間接觸和摩擦等有關。

4 結 論

利用ABAQUS 顯式分析算法分別對單層立管和八層非粘結柔性立管進行了碰撞影響特性計算，在考慮非粘結柔性立管骨架層和抗壓鎧裝層軸向材料屬性的基礎上，研究不同的碰撞速度、管間摩擦系數和管內壁壓的單因素條件，分析非粘結柔性立管碰撞過程中下游被撞管碰撞接觸區域的應變、應力及接觸力的影響規律，主要結論如下：

（1）在相同的碰撞速度、管間摩擦和管內內壓的條件下，在單層立管和多層非粘結柔性立管正向碰撞過程中均發生多次碰撞，且第一次碰撞過程中碰撞力遠大于其他碰撞過程，故第一次碰撞過程最為劇烈，因此應考慮第一次碰撞過程中碰撞應變和應力等變化規律。在第一次碰撞過程中，下游被撞單層立管碰撞區域沿碰撞方向的碰撞應變和應力隨碰撞速度的增加而增加；不同的是，八層非粘結柔性立管的應變和應力隨著碰撞速度的增加呈現先增加后減小的趨勢。

（2）類似地，隨著兩管外壁摩擦系數的增加，其對單層立管碰撞過程的接觸力幾乎無影響，對多層非粘結柔性立管碰撞力的影響是碰撞力呈先增加后減小的趨勢，同時管間摩擦的存在能降低八層管碰撞過程中的應力幅值，碰撞應力隨摩擦系數的增加表現出先減小后增加的趨勢，在摩擦系數為0.05時最小。

（3）隨著管內壁壓的增加，單層被撞管的應變、應力呈先增加后減小的趨勢，其對八層非粘結柔性立管的碰撞影響是隨著管壁內壓增加呈現增加的趨勢，且影響逐漸增強。對立管碰撞的碰撞力而言，單層管的碰撞表現出先增加后減小的趨勢，被撞非粘結柔性立管的碰撞力的幅值都隨管壁內壓呈先減小后增加的趨勢。

綜上所述，減小立管碰撞過程中的碰撞速度，選擇適宜的摩擦系數和內壓如0.05 MPa和1 MPa，能使碰撞過程的應力和應變以及碰撞力最小，碰撞過程的沖擊能最小，疲勞損傷也較小，增加服役期間立管和平臺系泊系統的安全性。非粘結柔性立管的碰撞影響規律研究可為下一步研究陡波型立管的碰撞影響規律提供一些參考。