基于R-NSGA-III 的常規導彈火力分配模型

劉子豪，董寶良，王寶寶，廉蘭平，程燦

（華北計算技術研究所系統四部，北京 100083）

常規導彈作戰方案評估主要是對常規導彈部隊作戰方案的可行性、風險度、作戰效益等進行的評價和估量[1]。如何提升作戰方案的可行性、作戰效益，降低風險度是研究重點和難點。

文獻[2]提出綜合考慮目標重要度、毀傷要求以及生存狀態等因素建立了輔助決策模型，文獻[3]提出建立了針對防御場景下的動態武器協同火力分配模型，該文在其基礎上考慮了某型號導彈存在調度轉移[4]和發射前準備時間等情況，在普通武器-目標模型[5]的基礎上，引入了導彈發射準備時間（時間成本）這一目標，輔助決策者選擇評估價值更高的方案。

武器-目標分配問題主要使用多目標進化算法進行求解，這類算法需要利用帕累托（Pareto）前沿找到相對優解或者最優解。非支配排序遺傳算法（NSGA-III）就是其中的典型代表，在處理多目標優化問題上具有較為廣泛的應用。但在輔助決策中，決策者并不需要得到全部Pareto 前沿，而只關心部分Pareto 前沿，或者只需要在特定區域獲得更多解。基于此，該文提出基于偏好點的NSGA-III 算法（R-NSGA-III）的常規導彈火力分配輔助決策模型，并通過實驗仿真驗證了模型可以得到最優打擊方案，能夠達到輔助決策作用。

1 簡介

該文提出基于R-NSGA-III 的常規導彈火力分配模型，優化目標包括最大化敵人的預期損失、最小化方案導彈的成本和最小化導彈發射任務準備的時間成本。模型主要針對的場景是在打擊目標給定條件下，對現有進入發射狀態和未進發射狀態的導彈進行任務分配。模型需要決策者輸入對三個目標的若干偏好，然后可生成多種近似并相對最優的打擊方案，并可以通過三維散點圖的方式對生成方案，并直觀地展示給決策者，以更好地輔助決策。

該文求解模型的算法是基于NSGA-III 算法進行改進的。當前主流用于解決火力分配的多目標優化算法還有MOEA/D[6]、粒子群[7]、NSGA-II[8]等。其中NSGA-III 算法在處理多目標優化問題上具有較為廣泛的研究[8,10-11]與應用[11-12]，但是該算法生成的完整Pareto 前沿并不全部是用戶關心的。實際上決策者偏好方案一般只集中在Pareto 前沿的部分區域，或者在偏好的區域獲得更多的方案等。所以該文采用了R-NSGA-III 算法[13]，該算法在NSGA-III 程序的基礎上，引入一種新的參考點生成方法，同時使用遺傳算子和生存選擇過程。

2 導彈目標分配輔助決策模型

2.1 基本假設

假設某次作戰行動中有M種可用導彈武器裝備,設武器集合為W，其中，wi表示第i類武器裝備，且第i類武器裝備有Mi個，則第i類武器裝備集合wi表示為Wi。有N個潛在打擊目標，目標集合為T，其中tk表示第k個潛在打擊目標。

文獻[14]圍繞導彈戰斗部打擊目標過程所涉及的毀傷評估研究進行總結概述，分別從目標毀傷評估模型、毀傷過程主體、分類目標毀傷、毀傷評估手段四方面進行闡述，梳理現有的主要成果。可抽象計算出第i類武器裝備打擊第k個打擊目標時的毀傷概率為pik，毀傷收益為vi，使用一個第i類導彈裝備所需要的成本為uj。參考文獻[15]和文獻[17]模型設導彈wij進入發射狀態所需時間為sij。

2.2 問題模型

M類武器聯合打擊所有潛在的目標時，對目標的毀傷效果如式（1）所示：

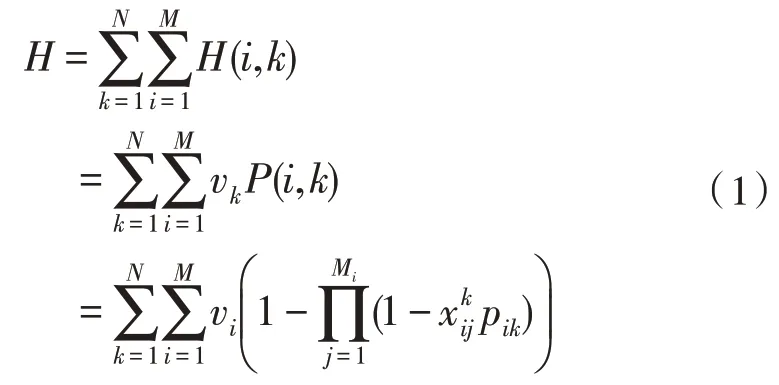
M類武器聯合打擊所有目標時，成本為使用的所有武器的成本之和，如式（2）所示：

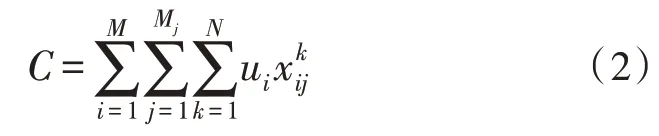
方案的導彈準備時間取導彈進入發射前的平均等待時間，如式（3）所示：

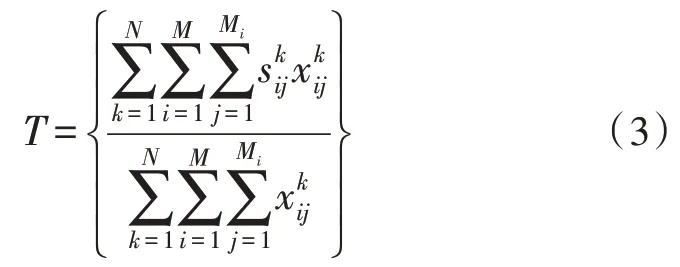
2.3 問題約束

確定武器裝備目標分配方案時需要滿足一些約束條件，建立優化模型的約束條件如下：

約束a：對于任意一個武器裝備，最多只能打擊一個目標，即一個武器裝備可以用于打擊某個目標，也可以閑置不打擊某個目標，如式（4）所示：

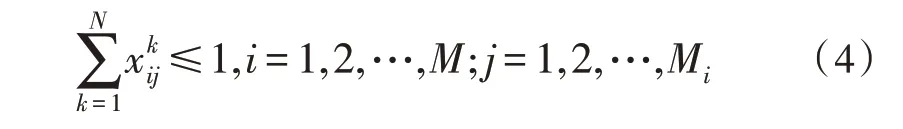
約束b：用于打擊同一目標的武器裝備種類數不超過某一閾值（假設預先設置的閾值為T），如式（5）所示：

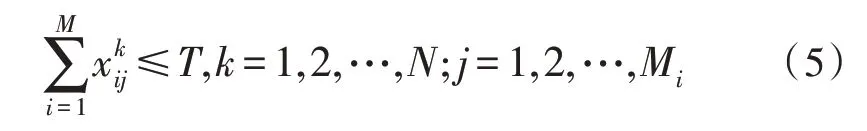
綜上，根據給出的目標函數和約束條件，確定武器裝備目標分配方案時以最大化單位成本上的毀傷效果為目標的優化模型，如式（6）所示：

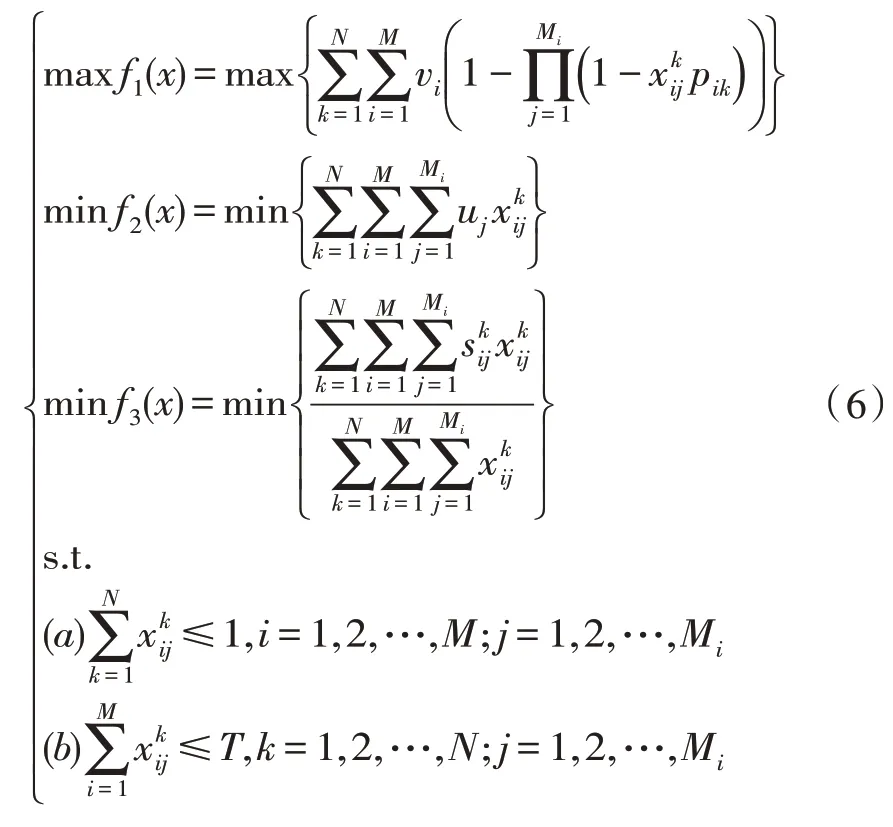
3 基于偏好點的NSGA-Ⅲ算法

3.1 NSGA-III算法

2014年，有文獻提出了NSGA-III算法，該程序通過引入一系列預定義的參考方向，彌補了NSGA-II無法擴展到三個以上目標的不足。該算法根據當前種群獲得覆蓋整個目標空間的超平面，并在超平面上生成一系列分布均勻的參考點。也有一些文獻[19]對該算法進行了改進，為該文提供了思路。由于該文提出的基于偏好點的NSGA-III 方法就是基于這種方法，所以，文中簡要描述其過程，算法流程圖如圖1 所示。

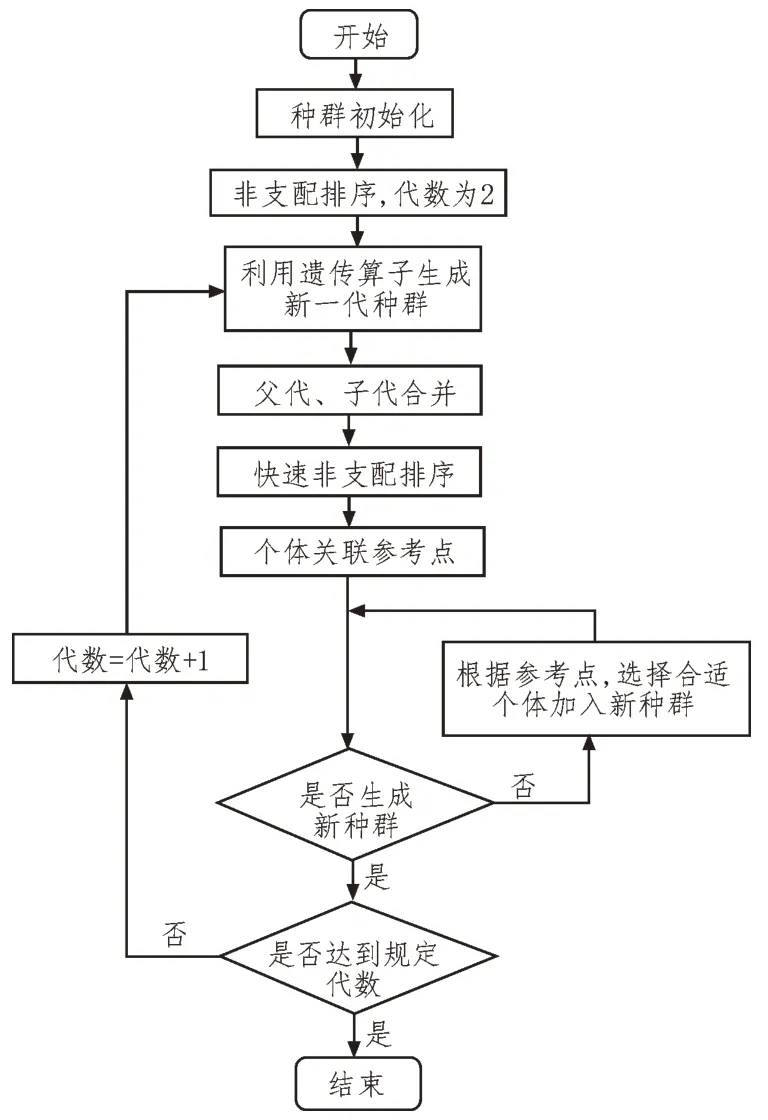
圖1 NSGA-III算法流程圖

NSGA-III 算法與NSGA-II 算法在父代、子代合并前的操作都是相同的。NSGA-III 算法首先利用Das-Dennis 方法在單位超平面上選取H個分布均勻的參考點，然后將每個參考點與原點相連接，參考方向為目標點方向。在每一代合并后的種群中，所有個體都根據系統的最大、最小值進行歸一化。然后，根據個體到參考方向的正交距離，將每個個體關聯到一個特定的參考方向，用一種小生境方法來選擇合適的個體加入新種群。這種方法不需要額外的選擇操作，因為總體大小幾乎保持與參考方向的數量相同。NSGA-III 算法在3-15 個目標的優化問題上進行了測試，在每種情況下，它都能夠在約束和無約束問題上找到一個收斂良好、分布良好的近Pareto最優解集。

3.2 基于偏好點的NSGA-III

R-NSGA-III 在NSGA-III 的基礎上進行了擴展，將決策者提供的偏好點作為參考，引入了一種新的參考點生成方法，同時使用與后者相同的遺傳算子和生存選擇過程。假設決策者提供了K個三目標模型的偏好點r(k)。

每個偏好點首先采用NSGA-III 的歸一化方法進行歸一化。根據每個目標的最大值fmax和最小值fmin，得到歸一化的偏好點如下:

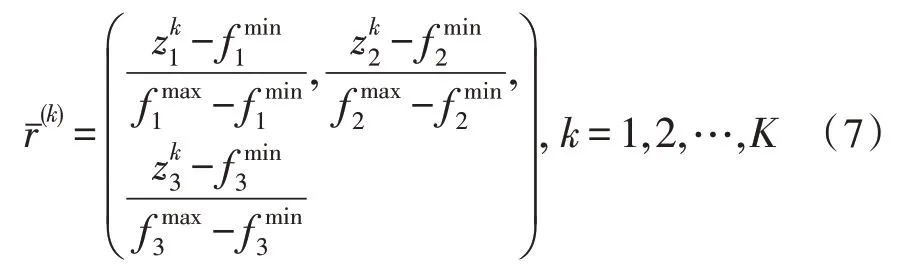
然后，計算單位超平面的截距和從理想點到每個標準化參考點的向量如下：

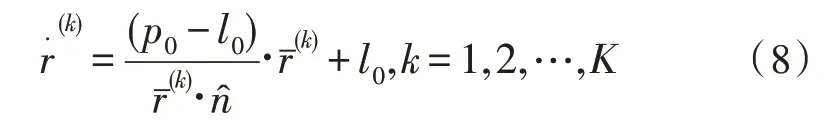
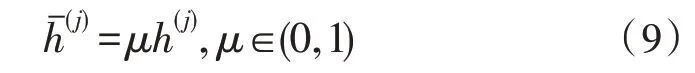
然后，利用Das-Dennis 參考點的質心g和形成的向量，將縮小后的Das-Dennis 參考點平移到單位超平面上，結果如下:

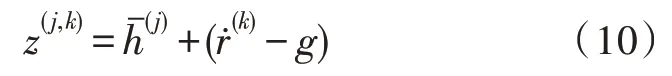
其中，gi為縮小的Das-Dennis 點的質心。

在完成上述操作之后，所有的Das-Dennis 參考點都位于以投影點為中心的三角小區域上。對K個偏好點逐一重復上述步驟。因此，將一共有K×H個參考點存儲在Za中。然后將三個由單位向量表示的極值點添加到集合Za上。

這使得Za的大小為(K·H+3)×3。為了后續可以更好地進行歸一化，添加極值點來創建極值的Pareto 最優解，并將這些點作為NSGA-III 算法中的參考點。因為標準化因子(fmax，fmin)在每一代中都會發生變化，所以要在每一代中都執行上述操作。在NSGA-III 運行結束時，除了極端參考方向對應的解外，只考慮原始參考點產生的每個參考方向的最接近解。

4 實驗結果及分析

4.1 實驗算例描述

假設我方本次進攻，擁有5 種導彈類型，每種類型的彈量平均為9 個，期望打擊的目標數量為7 個，算法人口為183。該文的初始數據為0 到1 之間隨機數。為貼合戰場實際情況，在此基礎上進行了修改。如選擇部分武器進入備戰狀態，準備的時間成本為0。部分毀傷能力強的武器未進入熱待機狀態，則準備時間會更長等。

對照組采用了NSGA-III 算法，并采用了相同的種群規模，生成兩組實例。決策者根據對三個目標的權衡給出偏好點，如表1 所示。

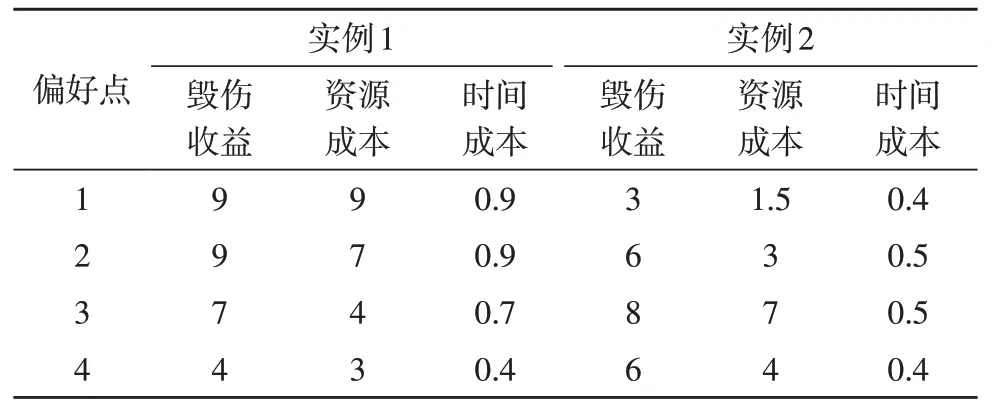
表1 偏好點

4.2 運行結果分析

為了更直觀地進行展示，作圖時用點的大小表示時間開銷的大小。實例1 兩種算法的運行結果如圖2-3 所示。

實例2 兩種算法的運行結果如圖4-5 所示。

如圖2-5 所示，該模型可以輔助決策者通過散點圖更直觀地了解到方案成本與收益的關系，快速地根據戰場情況篩選出符合當前時間要求的方案。

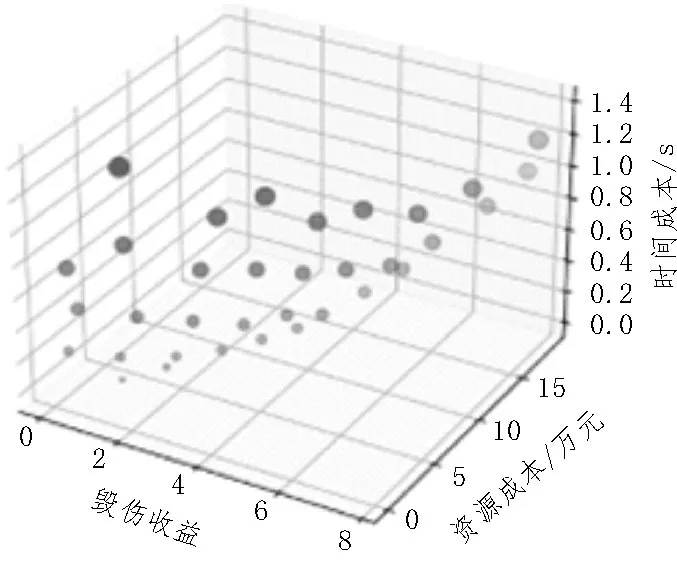
圖2 NSGA-III

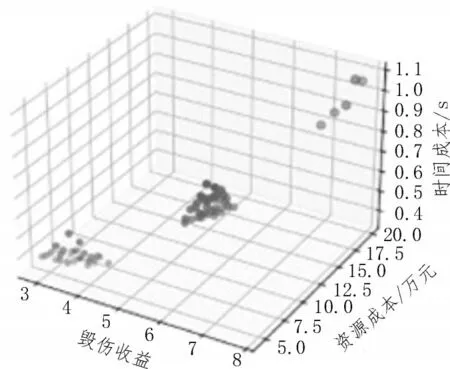
圖3 R-NSGA-III

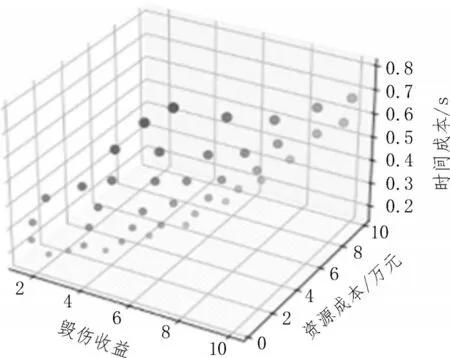
圖4 NSGA-III

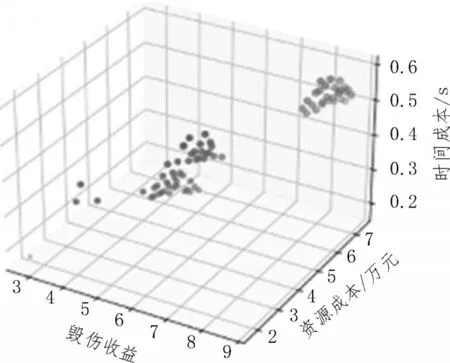
圖5 R-NSGA-III

橫向對比圖2-3和圖4-5可以看出，R-NSGA-III算法一方面可以根據決策者的偏好在相近區域提供更多解，而不是展示整個Pareto 最優前沿。另一方面偏好方案的區域是否有解也一目了然，可以讓決策者對我方裝備情況有額外的了解。

4.3 運行時間分析

在上述實驗的基礎上，該文又按照少打擊目標、少武器型號、多武器數量這三種情況，額外進行了三組不同的實驗來比較運算的時間開銷，每組實驗運行6 次取平均值。時間花費如表2 所示。

表2 運行時間對比

如表2所示，R-NSGA-III算法所花費的時間約為NSGA-III算法的52.05%。因此，可以驗證R-NSGAIII 算法時間開銷少，能夠更快地輔助決策。

5 結論

針對常規導彈的特點，引入時間成本可以讓決策者更詳細地了解方案情況，直觀地了解到偏好的指標是否有方案滿足。有利于決策者選出適宜的方案，更好地達到輔助決策目的。并且R-NAGA-III 算法運行時間開銷小，使得整體效率有大幅度的提升。綜上，基于R-NSGA-III 的常規導彈火力分配輔助決策模型貼近實際作戰，為智能決策提供有效的輔助支持，在對戰決策場景具有重要的實際應用價值。