基于Cohen-Sutherland編碼理論的光柵信號數字細分算法研究

王朝峰 張 玉 林江海

（山東省機械設計研究院，濟南 250031）

光柵是一種高精度測量儀器，被應用于高精度加工、檢查以及坐標方向測量。莫爾波紋是一種以光柵的相對移動為基礎的技術。因為該光柵的相對運動，傳輸光的光強會周期性改變。該光強信號被硅光單元轉換成具有周期變化的電子信號（正弦波），并在一組信號中進行一組處理，從而得到該光柵的相對位移。然而，單靠對其周期的估算遠遠無法達到準確的檢測要求。在計算機技術快速發展的今天，對莫爾條紋進行高階、高精度數字分割已經勢在必行。

數字化分割技術是一種新的、行之有效的方法，是目前國內外學者關注的一個熱點問題。當前，常用的數值劃分技術多采用軟件實現，如將“插值”與“四邊形”相結合，利用數學模型建立新的曲線方程式程[1-3]，即純粹的硬件劃分[4-5]。然而，這些技術中的細分技術數目較小（通常是500以下）且線路較多，容易造成信號干擾，影響有效信號。由于資料的準確性下降，資料加工困難，很難達到較高的解析度。

文中使用計算機軟件中的“大號”和“細分小號”相結合的方法進行劃分[6]。在細分方面，利用分段運算和正余切功能，既能提高分辨能力，又能保持線性特性。該方法利用快速計時器芯片進行運算，而小數運算通過軟件的分解來實現。莫爾條帶循環可逆算，而小數計數法則是莫爾條帶細分的一個周期。本文以光柵微機上的軟件為對象，在此基礎上利用Cohen-Sutherland編碼原理對相位劃分進行詳細的分析[7-8]。

1 數字細分理論

光柵測試裝置是利用光柵法實現對輸入量（位移、角度等）進行變換和輸出的一體化測試裝置。光柵測光的基本原理是利用光柵對來自光源的光進行調制，把機械位移量轉化為光學信號，并將其轉化為可根據光線的調制而改變的交流電信號。通過不同的加工、轉換，可以對不同的力學、形位進行對應的檢測。在測定長度時，光柵是以間隔W為單位的編碼標尺。如圖1所示，編碼標尺的同時，利用光柵作為基準進行對比和測定，可以從被測物體上讀出X，表達式為

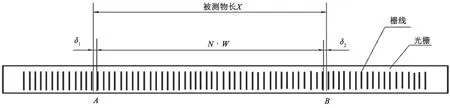
圖1 光柵精密測量定位原理

式中：N為AB間的光格計數；δ、δ1、δ2分別為在AB兩端對應的光格上讀取劃分的小數值。

可見，柵格的測量本質上是相應的格線N個數和少于節距的點數的總和。

如果測量精度允許對十進制值進行四舍五入，則可將方程式簡化為

因此，光柵長度可以通過簡單地讀取光柵柵線的數量N獲得。

如果測量精度不允許四舍五入到十進制值，則必須細分光柵間距。假設可以將間距細分為n個相等的部分，則柵格細分的分辨率為

此時，測得的小數部分為

式中：m=0,1,2,…,n。

將式（3）和式（4）代入到式（1），并令M=N·n+m，則

從而得到測量單位最小的系統方程。

實踐中，若以柵格角度或柵格角度為單位，僅可求出整列間隔，其數值精確性遠低于以上所提需求。為了達到要求的精確度，選取合適的柵格間隔進行劃分，然后通過對間隔的劃分獲取最低的讀出值來提高設備的解析度。需要說明的是，細分是指一條莫爾帶上的多條測量脈沖。

在傳統技術中，常采用細分法進行測量。該方法具有簡便、信號要求低的特點，適用于靜、動兩種不同的測量方式，但劃分數目較少。移位電阻鏈法是一種比較精細的測量方法，但是電路比較煩瑣，信號的正交性很強，且測量的準確率受到零漂的限制。振幅分裂電阻鏈方法具有精確性好的優勢，不會受到信號的幅值和振幅的影響，可以實現動靜兩方面檢測，但是線路比較煩瑣。鎖相細分法具有細分數量大、電路簡單以及信號不嚴謹等優點，只適用于動態檢測，但均勻性好，光柵運動高。載波法具有較大的細分能力和較高的準確率，但是線路比較煩瑣，同時其波形學和正交度比較高。

從上述結果可以看到，在需要進行大規模劃分時，若采用硬體劃分，將會造成較大的困難，并不適合于單純的硬件實施。莫爾條形碼的劃分是利用計算機程序對其進行劃分，再利用程序劃分，即利用采集與儲存的資料將莫爾條紋的兩個相位為90°的脈沖輸出信號進行數字化處理，并進行多次波形和數碼展示。利用計算機軟件細分，可以使裝置的硬件結構更加簡單，降低線路對有效信號的干擾，加強裝置的性能，改善裝置的準確度。

2 數字細分算法

如圖2所示，莫爾條帶在理論上并非正弦脈動，而在槽寬為W/2（也就是代表光柵的光透過部）和空隙為0時得到三角波形。然而，在現實的構造中，光柵的信號會改變。光束的不均勻性和光的衍射效應，光罩面間光的反射，光柵光罩的凹凸不平等，均會改變光柵信號，變化曲線接近圖3。

從圖3可以看出，在出相與暗相的光發射端，一個正弦波的信號被光器件生成。從圖2可以看出，按照光電變換的原則，光學信號被變換成電信號，此時仍然是正弦信號，可以用一個正弦波來代表

圖2 光柵理想信號

式中：U為光電元件輸出信號；W為光柵柵距；X為位移；Up-p為信號峰值；Ucp為直流電平。

與圖3相似，在光器件收到明暗色的正弦信號后，按照光電變換的原則，把該光學信號變換成電信號仍然是正弦波，也可以由式（6）來表達這個正弦波。

圖3 光柵實際信號

通過計算、區分、細分和小數計數等全周期，采用相角偏差90°的正弦型和余弦型進行測量。在幅度調節時，真實的信號U的幅度會隨著電源波動、光強度和光柵間距而變化。但是，由于氣溫等環境因素的作用，系統無法獲得精確的變形信息。

分析表明，當兩路莫爾條紋的振幅改變相同時，振幅U的波動效應可以用莫爾條帶的正弦和余弦比例來抵消，即這里U為振幅，θ為相位角度，由此確定位移。

在兩個莫爾條帶的幅度改變相同的條件下，可以用莫爾條帶的正弦與余弦之比排除幅度U起伏的效應，并隱藏一定的位移量。這樣可以根據得到的數值獲得相位角，進而得到相應的位移量。

以sin光柵信號與cos柵極信號的過零及其絕對等效處為界，將一柵格循環劃分為8個具有相位角度的區，并將8個區的基礎設為0、100、200、300、400、500、600以及700（此處是800個劃分實例，實踐中如果有必要，可以在該方案中增加劃分倍數），見圖4[9]。

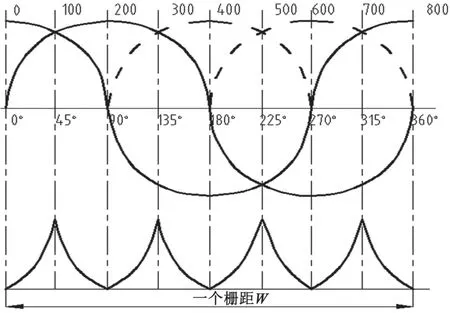
圖4 細分原理圖

利用以上劃分原則，將一個周期（0°～360°）的正弦波信號劃分為8個區間，各分區使用三位二值碼，右側為首位[7]。假設每一次獲得的兩個測量信號的數值是Usin、Ucos，編碼規則為：若Usin＞0，則第1位置1，否則為0；若Ucos＞0，則第2位置1，否則為0；若|Usin|-|Ucos|＞0，則第3位置1，否則為0。

根據該編碼規律，可以方便地求出各基元的編碼數值，方法如表1所示。

表1 區域外碼

相位角分成8個區域后，由三角函數圖像和性質可以得到區域外碼判別的方法，如表2所示。外碼中的每一位被置成1（真）或0（假），就能得到對應區域三位二進制代碼。

表2 區域基數與外碼對應表

由編碼規則很容易得到每個基數對應的編碼值。基于Cohen-Sutherland編碼理論的相位角區域編碼算法具體步驟如下。

步驟1：定義一個含有4個成員變量的類CCode，成員變量為all、sin、cos、sc。

步驟2：完成編碼。

步驟2-1：初始化CCode對象的成員變量all、sin、cos、sc分別為0；

步驟2-2：獲取測量信號值Usin、Ucos；

步驟2-3：如果Usin＞0，sin=1，否則sin=0；

步驟2-4：all+=sin；

步驟2-5：如果Ucos＞0，cos=1，否則cos=0；

步驟2-6：all+=cos；

步驟2-7：如果|Usin|-|Ucos|＞0，sc=1，否則sc=0；

步驟2-8：all+=sc。

步驟3：輸出編碼結果。

以表1中的區外代碼為基礎，識別獲取的數據，即尋找一個地區基礎數值，然后把該地區的基礎值和各分區的分區進行綜合，將一個循環的800次分割開來。對于在任意i上的一個信號數值，相應于這個位置的一個小的數值Xi為

按下列方式運行算法，計算每次獲取測量信號的外碼，由循環語句判斷該外碼值對應的區域基數。同時，根據外碼值的奇偶性，決定調用式（8）或式（9）計算對應區域的細分值。信號處理流程如圖5所示。

圖5 光柵信號處理流程

3 結語

從理論上研究了測量柵格的技術原理，提出了莫爾條紋細分算法。通過對通用齒形測試儀的實際使用，證明了所提方法可以對800個光柵格進行分割，50根/毫米的光柵解析儀的分辨率超過0.025 μm，具有較好的轉化效率。與傳統的硬件細分方法比較，它的精度可以達到1～2個百分點。試驗結果表明，該控制方案性能良好，工作性能穩定，并有較好的抗噪聲性能和很強的靈活性，能夠根據實際需求和計算機軟件實現精確劃分。