沖擊載荷下砂巖SHPB實驗的有限元模擬

陸 杉, 巫緒濤

(合肥工業大學 土木與水利工程學院,安徽 合肥 230009)

0 引 言

巖石是在不同地質條件下形成的一種天然材料,具有復雜的物理力學特性。在巖石工程中,爆破開挖是非常重要的施工方法。因此,研究巖石的動態力學性能具有非常重要的工程應用價值。目前,國內外廣泛采用分離式霍普金森壓桿(split Hopkinson pressure bar,SHPB)裝置對巖石材料進行高應變率實驗,研究其動態力學性能[1-2],但實驗僅能得到某種巖石材料在一維應力狀態、特定應變率下的力學參數,無法直接應用于復雜應力狀態的巖石工程中。因此,結合實驗、理論與數值方法得到巖石材料的本構模型,是實驗走向工程應用的關鍵環節之一。Holmquist-Johnson-Cook(HJC)模型是文獻[3]針對混凝土材料高應變率、大變形問題提出的一種損傷型本構模型,相關研究證實,基于該模型的數值模擬結果與實驗結果吻合較好,是目前混凝土材料數值模擬最常用的動態本構模型[4-6]。由于巖石與混凝土均為脆性材料,巖石在沖擊荷載下所發生的損傷與破壞,與混凝土材料非常相似,文獻[7-9]將HJC模型應用于巖石材料,但由于巖石材料的性質、動態實驗技術等方面的復雜性,相關研究尚不成熟。

本文以2種靜態抗壓強度相差較大的砂巖(紅砂巖、灰砂巖)SHPB的實驗結果為基礎,用LS-DYNA有限元軟件對SHPB實驗過程進行模擬,分析HJC本構模型部分關鍵參數的敏感性,通過不斷優化數值模擬結果,得到符合實驗結果的整套HJC模型參數,并總結出有效的HJC模型參數的獲得方法。

1 HJC模型簡介

HJC本構模型由屈服面方程、損傷演化方程和狀態方程3個部分組成,共有21個參數,其中包含基本物理力學參數、壓力參數、損傷參數和極限面(屈服面)參數[3]。

1.1 屈服面方程

HJC模型的屈服面方程為:

(1)

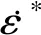
1.2 損傷演化方程

HJC模型損傷度用等效塑性應變與塑性體積應變的累積描述,其損傷演化方程為:

(2)

(3)

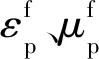
1.3 狀態方程

HJC模型采用分段式狀態方程描述材料靜水壓力(p)和體積應變(μ)之間的關系,如圖1所示。

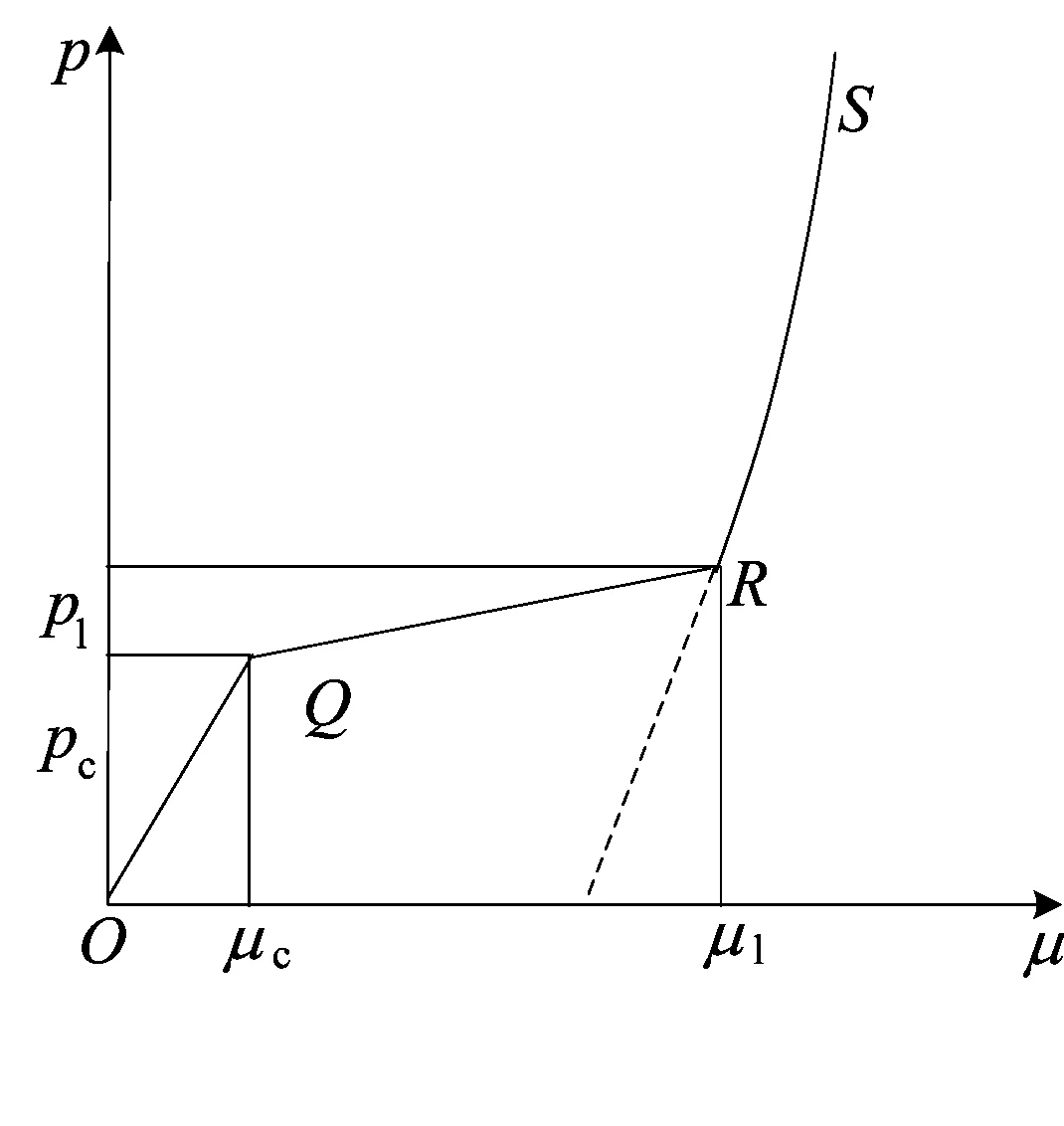
圖1 HJC模型靜水壓力-體積應變曲線

第1階段(OQ),為線彈性階段(p≤pc),在加載或卸載段,有

p=Keμ

(4)

Ke=pc/μc

(5)

其中:Ke為體積模量;pc、μc分別為單軸壓縮實驗的壓碎體積壓力和壓碎體積應變。

第2階段(QR),為塑性過段階段(pc≤p≤pl),此時材料內的空洞逐漸被壓縮從而產生塑性變形。在加載段,有

(6)

其中:pl為壓實壓力;μl為壓實體積應變。

在卸載段,有

p-pmax=[(1-F)Ke+FKl](μ-μmax)

(7)

F=(μmax-μc)/(μl-μc)

(8)

其中:Kl為塑性體積模量;pmax、μmax分別為卸載前達到的最大體積壓力和體積應變。

第3階段(RS),為完全密實階段(p≥pl),當壓力達到pl,材料內部氣孔被完全壓碎。在加載段,有

(9)

(10)

2 數值模擬和數據處理方法

2.1 有限元模型

按SHPB裝置的實際尺寸建立有限元模型，包括入射桿、巖石試樣和透射桿，如圖2所示。

圖2 SHPB實驗有限元模型

入射桿和透射桿直徑均為50 mm，長度分別為2 379、1 397 mm，采用相同的線彈性本構模型，密度ρ=7 850 kg/cm3,彈性模量E=210 GPa,泊松比ν=0.25。砂巖試樣尺寸為φ49 mm×25 mm,采用HJC本構模型。砂巖試樣和入射桿、透射桿的接觸類型設定為面-面侵蝕接觸,由于SHPB實驗中試樣和壓桿間均勻涂抹潤滑劑,有限元模擬忽略摩擦影響。為了與實驗條件完全一致,將實驗過程中采集到的入射應變波數據作為有限元模擬載荷,直接加到入射桿左端面全部節點上。

2.2 SHPB數據處理方法

數值模擬在實驗入射桿和透射桿貼片位置取相應的入射波εi(t)和透射波εt(t),按SHPB經典兩波法,重構試樣的應力-應變關系為:

(11)

σ(t)=Eεt(t)

(12)

其中:E、c0分別為壓桿的彈性模量和波速;l0為試樣長度。

3 紅砂巖HJC模型參數的確定

SHPB實驗選用紅砂巖和灰砂巖,其靜態抗壓強度分別為 80、40 MPa左右,2種砂巖材質均勻、顆粒組成細膩、致密性好,均可視為均勻材料。2種砂巖HJC模型參數的確定方法一致,為節省篇幅,以下僅對紅砂巖進行詳細討論。

3.1 基本物理力學參數的確定

HJC模型中,基本物理力學參數包括fc、E、切變模量G、ν、Ke、T和ρ。其中,ρ、E、ν、fc、T可由實驗提前獲得,G、Ke計算公式為:

(13)

(14)

紅砂巖的基本物理力學參數見表1所列。

表1 紅砂巖基本物理力學參數

3.2 壓力參數的確定

HJC模型中,壓力參數包含pc、μc、p1、μl、kl、k2和k3,由3.1節已得參數,結合公式pc=fc/3,μc=pc/Ke,可以得到pc、μc。由于本文研究的應變率范圍較窄,試樣未進入壓實段,故參數pl、μl、kl、k2和k3采用原始數據。最終確定的壓力參數見表2所列。

表2 紅砂巖壓力參數取值

3.3 損傷參數的確定

損傷參數的改變,對于材料應力-應變曲線的影響極小,文獻[4-6]的研究表明,改變HJC模型參數中的Dl、D2與塑性應變最小值εfmin對擬合結果的影響極小,因此損傷參數Dl、D2和εfmin采用原始數據,Dl=0.04,D2=1.0,εfmin=0.01。

3.4 極限面參數的確定

由上述研究內容可知,除極限面(屈服面)參數A、B、N和材料應變率系數C值外,HJC模型的其余參數均可通過公式和簡單的實驗獲得。關于巖石等脆性材料的沖擊問題,HJC模型的極限面參數取值大多與原始參數保持一致,即A=0.79、B=1.6、N=0.61,該數值是根據單軸抗壓強度為48 MPa的混凝土來確定的,能否直接用于巖石類材料值得商榷。因此,本文根據已建立的模型,保持其余參數不變,通過單獨改變極限面參數的方式來研究其對巖石重構應力-應變曲線的影響。A、B值改變對紅砂巖HJC本構曲線的影響如圖3所示。

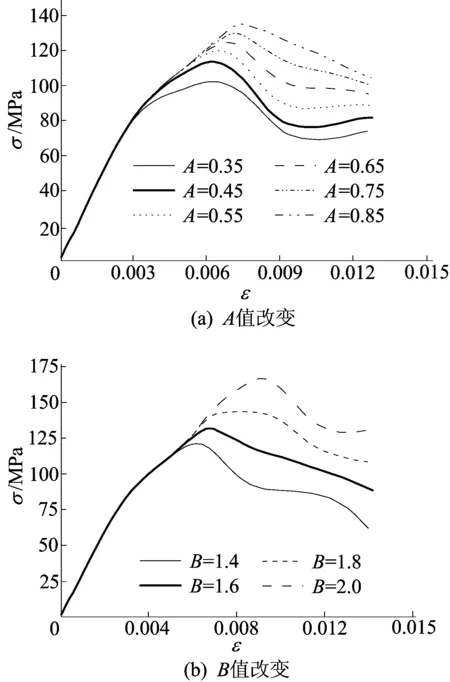
圖3 參數A、B對紅砂巖HJC模型應力-應變曲線的影響

3.4.1 參數A的影響

根據文獻[10],A取值范圍為0.35～0.95。由圖3a可知,A值由0.35依次增大到0.85的過程中,每增長0.10對應的峰值點應力分別為102.1、113.7、119.7、124.5、129.0、133.5 MPa,增長率分別為11.3%、5.3%、4.0%、3.6%、3.5%;峰值點應變分別為 0.006 15、0.006 20、0.006 45、0.006 73、0.007 05、0.007 42,增長率分別為0.8%、4.0%、4.3%、4.8%、5.3%。從圖3a可以看出,隨A值增大,應力-應變曲線塑性硬化段的斜率增加并趨于穩定,峰值點對應的應力和應變逐漸增大,但增長幅度不同。其中峰值點應力隨著A值增加,增長幅度逐漸降低,A值越小,增長率越大;峰值點應變則與之相反。

3.4.2 參數B的影響

B的取值范圍[10]為1.4～2.0。由圖3b可知,在B值從1.4按0.2的增量依次增大到2.0的過程中,巖石應力-應變曲線峰值點逐步往右前方移動,峰值點應力與應變均有顯著增長,但增長規律不同。

隨著B值增加,峰值應力增長率逐漸增大,B值增加至2.0時,增長率達到最大,B值越大,影響幅度越大;峰值應變隨著B值增加,增長率先迅速增加,達到最大值后又迅速減小,B值在1.6左右對峰值應變的影響最顯著。

3.4.3 參數N、C的影響

模擬發現,隨著N值增大,巖石應力-應變曲線的峰值應力和峰值應變都有一定程度減小,曲線的寬度略變窄,塑性段斜率逐漸降低,這表明材料處于一個逐漸軟化的過程。

C值在0.004～0.008之間變化[10],巖石應力-應變曲線的峰值應力有所增加,但峰值應變幾乎沒有變化。通過分析 (1) 式,可得出C值控制的是應變率效應在整個屈服面方程中所占的比例,它的調整能改變峰值應力的大小,對應力-應變曲線的整體形態沒有影響。

3.4.4 參數A、B、N、C取值的確定

由上述分析可知,適當調整材料的內聚力強度A、歸一化壓力硬化系數B及壓力硬化指數N值可改變巖石應力-應變曲線塑性硬化段斜率與寬度、峰值應力和峰值應變的大小,調整應變率系數C可略微改變峰值應力的大小。據此,綜合考慮各個參數的影響和控制的物理意義,優化得出A、B、N、C的值,分別為0.92、1.60、0.81、0.008。

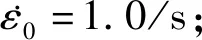
用上述HJC模型參數進行數值模擬,模擬結果與SHPB實驗結果對比如圖4所示。

從整體上看,無論是原始的入射波、反射波和透射波,還是重構的應力-應變曲線,數值模擬結果均與實驗結果吻合很好。

在低應變率條件下,數值模擬應力-應變曲線的峰值應力和應變分別為153.9 MPa、0.009 99,實驗數值為154.3 MPa、0.009 38,誤差率分別為0.3%、6.1%;中高應變率條件下,數值模擬曲線峰值應力和應變分別為166.6 MPa、0.009 85,實驗數值為169.0 MPa、0.009 91,誤差率分別為1.4%、0.6%。2種應變率情形下的誤差率均小于10%,由此可知,本文所獲得的紅砂巖HJC模型參數是合理的。

圖4 紅砂巖數值模擬與實驗結果對比

4 灰砂巖HJC模型參數的確定

為進一步驗證上述紅砂巖HJC模型參數獲得方法的可行性,本文對灰砂巖進行類似研究,得出灰砂巖HJC模型參數,見表3所列。

灰砂巖數值模擬結果與實驗結果對比如圖5所示。

表3 灰砂巖HJC模型參數

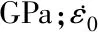
圖5 灰砂巖數值模擬與實驗結果對比

從整體上看,低應變和中高應變荷載下,數值模擬曲線與實驗數據較為吻合。低應變率條件下,灰砂巖數值模擬曲線的峰值應力和應變分別為86.4 MPa、0.008 97,實驗數值為87.7 MPa、0.008 29,誤差率分別為1.5%、7.6%;中高應變率條件下,數值模擬曲線峰值應力和應變分別為92.5 MPa、0.010 16,實驗數值為94.3 MPa、0.010 77,誤差率分別為1.9%、6.0%。2種應變率情形下的誤差率均小于10%,在容許范圍內。由此可得,本文HJC本構模型參數的確定方法是可行有效的。

5 結 論

本文為了得到砂巖HJC本構模型的所有參數,使用非線性有限元動力分析軟件LS-DYNA對砂巖SHPB實驗進行數值模擬,研究結果表明,無論是紅砂巖還是灰砂巖,數值模擬結果與實驗結果吻合較好,本文數值模擬所使用的建模方法、模型參數、材料模型等都是合理的。

(1) 直接用實驗采集入射波作為數值模擬的壓桿端面載荷,可以避免因波形彌散導致模擬條件與實驗條件的差異。

(2) HJC模型的21個參數中,具有較高敏感性的參數為A、B、C和N。其中A、B和N的取值對數值模擬的應力-應變曲線峰值點影響較大;隨著A、B取值增大,峰值應力和應變均有較大幅度增大;隨著N值增大,峰值應力和應變有減小趨勢;C值可以較好反映材料的應變率效應。

(3) 本文將 HJC 模型推廣到砂巖材料中,獲得了紅砂巖與灰砂巖2種巖石的HJC模型參數,給出砂巖材料HJC模型參數的確定方法,并驗證了其有效性。