GNSS形變監測時間序列的粗差數據處理方法

王民頓 尚俊娜

1 杭州電子科技大學通信工程學院，杭州市白楊街道2號大街1158號，310018

常用的GNSS時間序列粗差剔除方法主要有3σ法、中位數(MAD)法、四分位距(inter quartile range，IQR)法等[1-6]，但這3種方法都有一個共同的缺陷——數據剔除的效果在很大程度上受限于數據長度，以至于無法把握真實的數據趨勢[7]。為解決這個問題，可以采用滑動窗口的方式一段一段地剔除數據，但這會增加更多的限制，而且還會受到窗口選取的影響。

本文針對窗口難以選取的問題提出一種基于小波分析的一階導數粗差剔除法，經過仿真模型及實際驗證，解決了傳統粗差探測算法在數據處理中的過剔除現象，在小波分析過程中能準確提取到信號的真實形變趨勢，盡可能多地區分出粗差點；同時，在粗差點采用廣義延拓插值補點，兼顧了監測數據的連續性。

1 GNSS形變監測時間序列的粗差數據處理方法

1.1 基于小波分析的一階導數粗差剔除法

基于小波分析的一階導數粗差剔除法步驟如下：

1)首先引入一階導數分析信號趨勢項。將信號求一階導數后，會得到類似高尺度下的小波系數，借用小波閾值的思想，原本小波閾值函數是將信號中低幅值的小波系數進行過濾，現在則認為大于閾值的一階導數點是粗差點。

2)利用小波原有的minimaxi法則求出閾值，以分離異常導數值，這里采用經驗方程。如果要達到更好的效果，可以在閾值的設定方面進行拓展，這與小波閾值的設計相同，將其標志成為異常點，大部分異常點會在此被剔除。閾值計算公式為：

(1)

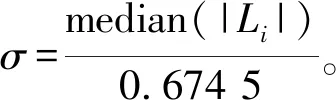
3)將剔除后的數據只進行1次3σ剔除，此處也可以選取大一點的判決門限(如5σ等)防止剔除了有用信號。

4)最后借用小波分析的手段對數據進行粗差剔除，其主要方式是通過小波分解得到低頻趨勢項，將原信號和低頻趨勢項作差得到殘差。考慮到重復計算趨勢項會大幅增加計算量，這里只求1次趨勢項，對獲取到的殘差進行拉依達準則(3σ準則)計算。將異常點置0(這里的異常點指的是偏離趨勢項的異常值)，殘差就會慢慢向0收縮，最后將殘差為0對應的原始信號點進行剔除。

1.2 形變監測缺失數據的廣義延拓插值法

粗差剔除后，原始信號中會存在信號間斷及數據缺失，為使監測數據連續，需要進行插值運算，本文采用廣義延拓插值法進行數據填補。廣義延拓吸取現有插值法和擬合法的長處與特點，采用分片光滑的做法，利用延拓域構建單元域擬合函數，并鎖定單元域邊界節點，以逼近最好效果。

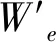
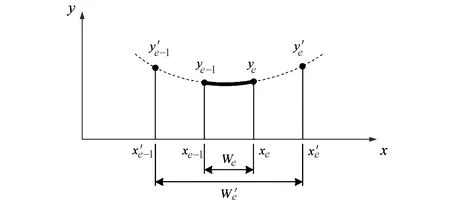
圖1 延拓域及相應函數值Fig.1 Continuation domain and correspondingfunction value

在延拓域構建逼近函數ye(x)：

(2)

建立廣義延拓逼近內插模型：

(3)

式中，I(a1,a2,…,aj)為逼近函數與先驗值的誤差。

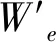
綜上，本文GNSS形變時間序列粗差數據處理流程見圖2。

圖2 數據處理流程Fig.2 Data processing flow

2 實驗及分析

2.1 模擬驗證

為驗證新算法的有效性，模擬GNSS形變的坐標時間序列，其原始表達式為：

(4)

采樣頻率為1 Hz，取4 096個歷元，考慮到實際形變監測過程中粗差數量多、分布范圍廣，在原始信號中添加10倍標準差的粗差點，粗差點數為500個，占比為12.22%(圖3)。采用3σ法、MAD法、四分位距法和一階導數小波剔除法進行對比，小波基選擇為db1～db5，分別作1～8層分解并計算剔除率，仿真次數為10 000次，結果見表1和2。

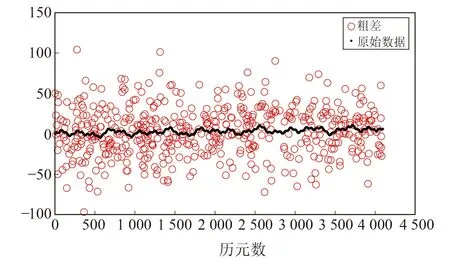
圖3 原始數據及全部粗差Fig.3 Raw data and all gross errors

表1 常規粗差剔除法的剔除率

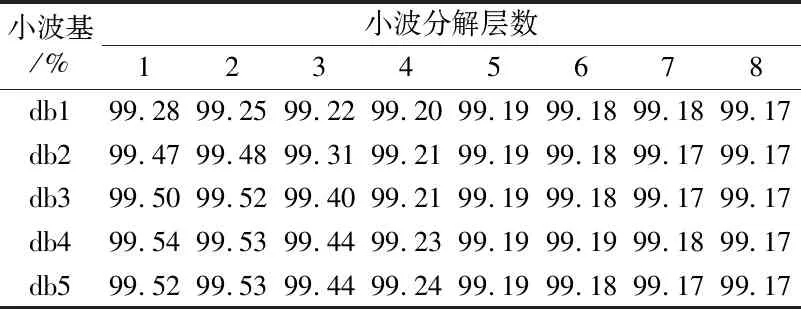
表2 一階導數小波剔除法在不同小波分解情況的剔除率

從表2可見，除db1外其他幾種小波使用效果基本相似，說明對粗差影響最大的是分解層數。由于增加小波分解層數會大幅增加運算量，即可以隨意選取一組小波基作一層分解，本文后續都采用基函數db4進行一層分解。

4種粗差剔除法效果對比見圖4，可以看出，一階導數的小波剔除率遠高于其他3種傳統粗差剔除算法，幾乎能探測到所有的粗差點。最后將圖4(d)剔除后的信號分別進行廣義延拓插值、分段三次樣條插值(spline)、相鄰非缺失值的線性插值(linear)、保形分段三次樣條插值(pchip)及修正Akima三次Hermite插值(makima)，并對比原始信號計算RMSE來評價插值效果，結果如表3所示。可以看出，廣義延拓插值效果優于其余插值方法，故將其應用于后續計算。

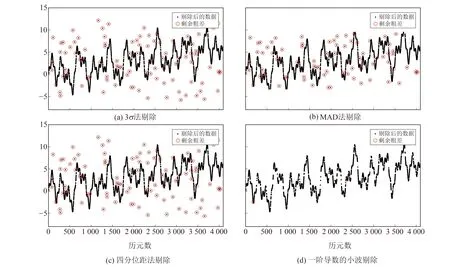
圖4 4種粗差剔除法剔除效果Fig.4 Four gross error elimination methods

表3 插值精度對比

2.2 工程實例測試

本文使用富陽市金鑫廣場桁架張拉測試時的數據，時間跨度為2020-10-26～27，共47 561個歷元。監測拆除施工輔助支架桁架下沉時高度數據的變化情況，現場遍布高壓電線和信號基站，使監測設備終端接收信號產生干擾，造成原始數據存在許多粗差點，真實波形難以觀察。由于真實信號未知，對原始含噪數據采用移動中位數進行平滑處理，得到近似的真實信號，窗口長度為200。

從圖5(a)～5(c)可以看出，傳統粗差算法難以準確還原信號的原有趨勢，而一階導數的小波剔除法保留了信號的有用成分。為達到較好的剔除效果，3種傳統算法每次需要剔除1個點后再重新將剩余數據進行相同的操作，4種粗差剔除算法運行時間結果見表4。

表4 算法執行速度

由于MAD法和四分位距法需要計算中位數和百分位數，所以花費時間較多，而本文提出的新算法所用時間僅是3σ法的0.01倍。粗差剔除的正確性會影響到插值算法的效果，故將4組算法得到的剔除數據與原始數據進行精度對比，并挑選精度最高的進行廣義延拓插值，以補充剔除位置的數據。

由于真實信號采用的是原始信號平滑濾波后的數據，因此除了RMSE外，同時使用均值偏離量u作為精度評價指標，其計算公式為：

(5)

式中，s為平滑濾波后的真實信號近似，s′為經過粗差剔除后剩余的信號，q和p分別為2個信號的總長度。

圖5 金鑫廣場桁架形變監測數據及粗差剔除效果Fig.5 Jinxin square truss deformation monitoring data and gross error removal effect

從表5可見，前4種算法的RMSE較為接近，說明這4種算法都可以剔除影響較大的誤差。3σ法、MAD法和四分位距法存在過剔除現象，所以剔除后信號的均值與真實值存在較大的偏離，而一階導數小波剔除法能夠避免窗口的選取，經過廣義延拓插值后與真實值僅存在約0.03 mm的偏離。

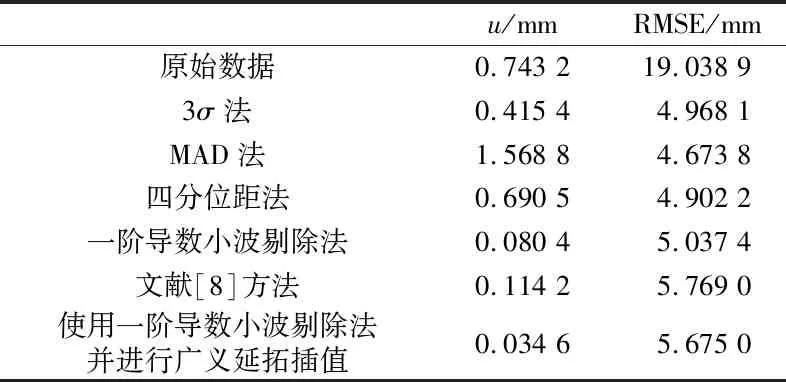
表5 精度對比

3 結 語

針對GNSS形變監測的傳統粗差探測算法性能受限于數據長度的問題，提出基于小波分析的一階導數粗差剔除法。采用原始信號的一階導數來區分正常波動和粗差異常，可以有效避免窗口數據的選擇，而且只進行1次一階導數的剔除，大幅減少了計算量；同時，在粗差點采用廣義延拓插值補點，保證了監測數據的連續性。經實例驗證，本文算法的計算效率和準確度都較傳統算法有較大提升。