舵機變梯度負載機構設計與扭桿彈簧優化

吳 宇 鄧孔全 雷乾勇

（貴州航天林泉電機有限公司，貴州 貴陽 550081）

0 引言

舵機即控制舵面的伺服電機，作為控制飛行器運行姿態的核心執行機構，其功能是根據控制系統的控制指令，驅動調節機構執行相應的動作，以產生對分系統的操縱力矩，從而控制飛行器運行姿態[1]。因此，對舵機的性能指標考核至關重要。

為了驗證舵機在高空復雜環境下能否保持良好工作狀態，通常需要利用負載模擬機構來對舵機舵軸施加鉸鏈力矩，從而模擬飛行器的各種運行工況，測試舵機各項動態參數[2]。

現階段的舵機負載模擬機構多為單通道低負載特性，雖體積小、易維護，但難以完成多通道的復雜工況模擬任務。同時，同種舵機的變工況測試和不同舵機的應用工況不同也對負載模擬機構的通用性提出了更高的要求。該文設計了一套十字四通道變梯度負載模擬機構，對其采用的正方形截面扭桿彈簧進行結構設計與參數優化，并利用有限元分析軟件ANSYS/Workbench完成靜力學仿真與優化驗證，確保機構測試性能滿足設計需求。

1 工作原理

舵機變梯度負載機構通過控制系統驅動舵機對主軸施加扭矩，扭矩傳遞至扭桿彈簧，導致其沿軸向扭轉變形，扭桿彈簧固定端由扭矩傳感器反饋扭矩大小，扭桿加力端由旋轉編碼器反饋旋轉角度。移動扭桿彈簧固定端整體機構能夠調整扭桿彈簧受扭長度，不同的受扭長度能夠施加不同的扭矩梯度，工作原理如圖1所示。

2 整體機構設計

變梯度負載模擬機構設置十字4工位，主要結構由中空雙法蘭扭矩傳感器、旋轉編碼器、方形扭桿、扭桿連接機構、支座、傳動主軸、十字聯軸節和十字鑄鐵平臺等組成，設備尺寸（長×寬×高）為2.2 m×2.2 m×0.6 m，整體結構如圖2所示。

3 詳細結構設計

3.1 扭桿連接機構

扭桿連接機構分為固定端和加力端，其結構如圖3所示。扭桿的固定端和加力端的其中一側分別與扭矩傳感器法蘭和傳動主軸連接，另一側則為扭桿彈簧連接機構。扭桿連接機構采用壓塊下壓夾緊塊，從而抱緊扭桿連接件的方式，進而固定扭桿。扭桿連接件開孔尺寸與扭桿截面尺寸間隙配合，并在孔一側開1 mm縫隙，利于夾緊和松開扭桿，如果后續需要更改扭桿截面尺寸，僅需要更換扭桿連接件即可。扭桿連接件受壓部分設計為與壓緊塊相互配合的方形面，以保證在大力矩條件下不打滑。

3.2 主軸機構

主軸用于連接舵機軸與扭桿，整體采用十字聯軸節分體結構，外加固定套筒保護。軸身利用角接觸軸承和軸承端蓋固定在主軸基座上，軸承端蓋下部銑扁是為了安裝旋轉編碼器固定條。十字聯軸節與舵機連接端可根據相應型號尺寸單獨定制，主軸機構如圖4所示。

3.3 中空雙法蘭靜態扭矩傳感器

鑒于設計要求梯度可變，需要能夠調整扭桿受扭長度，因此選擇雙法蘭靜態扭矩傳感器來實現設備扭矩檢測與反饋，其內部有軸向中空結構，兩端均為法蘭盤連接，一端與扭矩傳感器固定支座連接，另一端與扭桿固定端連接。根據設計需求，選擇量程為300 N·m、測試精度為0.1%的扭矩傳感器。

3.4 中空旋轉編碼器

旋轉編碼器，也叫角度傳感器。根據需求，選用分辨率為40000（旋轉角度精度為0.5'）的中空旋轉編碼器，安裝于主軸上，檢測與反饋旋轉角度。

3.5 正方形截面扭桿彈簧

作為負載機構的關鍵部件，扭桿彈簧性能的好壞直接關系到舵機負載模擬器的性能與加載精度。該文扭桿彈簧設計要求負載力矩范圍為0 N·m～80 N·m，能夠滿足2個（2 N·m/°和10 N·m/°）力矩梯度，且測試力矩精度須低于1%。

3.5.1 材料選擇

扭桿彈簧采用彈簧鋼加工，常用的材料有50CrV、60Si2MnA和45CrNiMoVA等，其中45CrNiMoVA因其優良的淬透性和機械性能而得到廣泛應用[3]。結合該文設計的模擬加載器需求，扭桿彈簧的材料選擇45CrNiMoVA，其抗拉強度和屈服強度分別為1470 MPa和1325 MPa。

3.5.2 尺寸參數計算

正方形截面扭桿彈簧受載時軸向旋轉角度如公式（1）所示。

式中：T為扭桿彈簧所受的扭矩；L為扭桿彈簧的等效受扭長度；a為扭桿彈簧正方形截面邊長；β為無量綱量，取β=0.141；G為材料的剪切模量，取G≈80000 MPa。

因為扭桿彈簧承受的載荷和軸向轉角呈線性關系，所以加載梯度即為常數，如公式（2）所示。

由公式（1）和公式（2）導出扭桿彈簧的加載梯度K與等效受扭長度L、正方形截面邊長a的關系，如公式（3）所示。

設計要求加載梯度須滿足2 N·m/°和10 N·m/°，考慮加載機構的整體尺寸限制和加工因素的影響，設計了3種加載梯度范圍不同的扭桿彈簧，扭桿彈簧參數計算結果見表1。

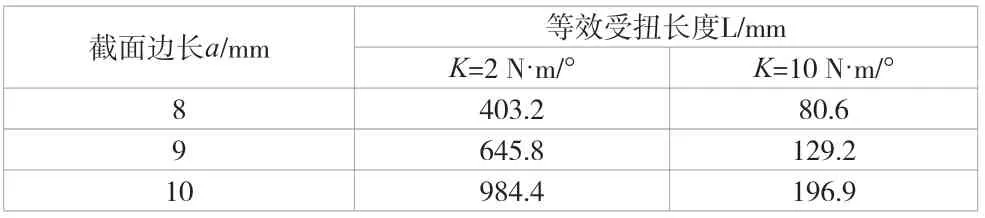
表1 正方形截面扭桿彈簧參數計算結果

由計算結果可知，結合設備臺面長寬尺寸要求，初步確定扭桿彈簧截面尺寸為8 mm×8 mm，當等效受扭長度為403.2 mm和80.6 mm時，能夠分別滿足2 N·m/°和10 N·m/°的加載梯度。利用ANSYS/Workbench對初步方案進行靜力學仿真，模擬工況為80 N·m載荷，結果如圖5所示。仿真結果顯示，該尺寸的方形截面扭桿彈簧所受最大應力為1513.4 MPa，遠大于45CrNiMoVA自身1470 MPa的抗拉強度和1325 MPa的屈服強度，該狀態下扭桿彈簧容易發生塑性變形甚至斷裂，因此需要對其進行優化設計。

4 扭桿彈簧結構優化

在設計扭桿彈簧結構參數的過程中，必須在確保扭桿彈簧剛度值的同時，避免其超出由自身工作壽命和受載強度所確定的扭桿應力值，且結構尺寸能夠滿足設備整體結構要求，因此有必要針對扭桿彈簧的結構尺寸建立優化設計數學模型。

4.1 確定優化設計變量

根據正方形截面扭桿彈簧變形能計算，以彈簧的等效受扭長度L、正方形截面邊長a為設計變量，如公式（4）所示。

4.2 確定優化目標函數

優化目標函數即為讓扭桿彈簧結構既不高于許用應力，又保證扭桿彈簧變形能控制在一定的范圍內，且具有更優越的性能，優化目標函數如公式（5）所示。

式中：Us為扭桿彈簧變形能；τmax為扭桿彈簧最大扭轉應力；S為正方形截面面積；G為材料的剪切彈性模量。

根據正方形截面面積計算公式S=a2和該類截面形式的扭轉應力公式（公式（6））就可以確定扭桿彈簧的優化目標函數，如公式（7）所示。

式中：Mn為扭桿彈簧負載扭矩；Wn為扭桿彈簧的抗扭端面系數；F為扭桿彈簧平衡狀態下所受扭臂力；l為扭桿彈簧導向機構的杠桿臂長；a為扭桿彈簧正方形截面邊長；[τ]為扭桿彈簧的最大許用應力。

4.3 確定約束條件

由于扭桿彈簧剛度k受扭臂力F作用，因此可以計算其形變量和扭桿彈簧剛度，如公式（8）和公式（9）所示。

剛度與強度約束條件分別如公式（10）和公式（11）所示。

扭桿彈簧等效受扭長度和正方形截面邊長約束條件如公式（12）所示。

4.4 目標函數求解

非線性規劃問題的求解實際就是找出指定條件下扭桿彈簧優化設計的最優解。針對目標函數求解過程中保證具有最大的扭桿變形能為原則，選取約束條件內的最小扭桿剛度[4]。目標函數求解邏輯如圖6所示。

4 .5 結果分析

以先前根據需求加載梯度計算的扭桿尺寸為參考，利用上述求解方法對方形截面扭桿彈簧進行結構參數優化。以80 N·m極限工況為加載條件，結合有限元分析軟件ANSYS/Workbench對其進行靜力學仿真與優化分析，得到3種優化方案，見表2。

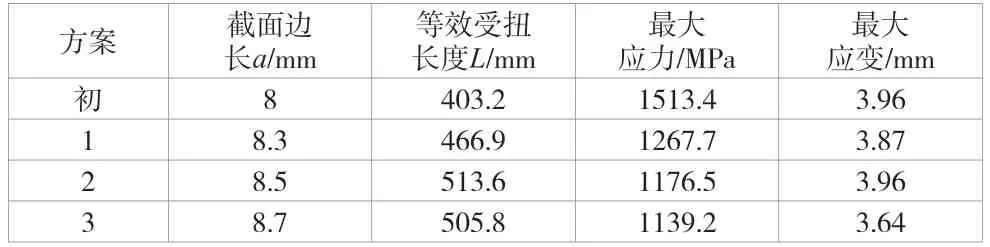
表2 原方案與優化方案參數

由表2可知，方案2因其在約束條件下存在較小的應力峰值和較大的變形量而成為最優方案，優化后的扭桿彈簧截面邊長a為8.5 mm，等效受扭長度L為513.6 mm，由扭桿應力、應變云圖（圖7）可知，扭桿彈簧所受最大應力為1176.5 MPa，最大應變為3.96 mm。當等效受扭長度為513.6 mm和102.7 mm時，能夠分別滿足2 N·m/°和10 N·m/°的加載梯度。

5 結語

該文根據需求設計了一套十字四通道變梯度負載模擬機構，利用十字臺座實現多通道負載模擬，鍵槽直線導軌結合中空雙法蘭扭矩傳感器與中空旋轉編碼器實現梯度可調功能，并對扭桿彈簧結構參數進行計算和有限元仿真驗證，初步驗證結果顯示其所受應力峰值大于該材料自身的許用應力，因此需要對扭桿彈簧結構參數進行優化。通過建立目標優化函數和約束條件，并利用ANSYS/Workbench完成參數仿真驗證，最終得到最優方案，確定了扭桿彈簧截面邊長為8.5 mm，等效受扭長度為513.6 mm，結果表明優化后的扭桿彈簧性能參數得到顯著提升，同時也滿足設計需求的結構和力矩梯度范圍。