基于電子傳動比的多邊形軸類零件數控車床工作原理及其誤差分析

倪明威，羅紅波

基于電子傳動比的多邊形軸類零件數控車床工作原理及其誤差分析

倪明威，羅紅波

（四川大學 機械工程學院，四川 成都 610065）

多邊形軸類零件具有無鍵連接的特性，在許多傳動場景中應用甚廣，但傳統加工方法存在精度低、效率低等缺點。近年來提出了兩軸同向轉動車削加工多邊形軸的方法，本文旨在根據該方法減小數控車床在車削加工多邊形軸時產生的平面度誤差。基于多邊形軸的成型原理，建立刀尖軌跡幾何模型并分析得出了刀尖的軌跡方程，將刀尖軌跡方程代入MATLAB仿真得到了不同邊數的多邊形軸截面的仿真軌跡。對仿真軌跡進行幾何分析后得到了截面直線度誤差的表達式，即可以在實際加工通過調整加工參數來獲得符合要求的加工誤差。根據以上方法，最后得到了不同邊形滿足項目要求的平面度誤差（不超過0.025 μm）所需要的加工參數。

電子傳動比；多邊形軸；誤差分析；MATLAB仿真

多邊形軸類零件常應用于高轉速、傳遞較大扭矩等加工場景中，目前在航空、航天、發電等設備制造中關鍵零件應用較多。現有的數控機床加工工藝是回轉體表面在數控車床上加工、多面體表面在數控銑床上加工，其缺點一是工件需二次裝夾、帶來定位誤差，二是難以達到高精度零件回轉體表面與多面體表面的位置精度要求、同時降低加工效率。另一種方案則是用車床通過回轉運動加工多邊形軸類零件，其截面成型原理為內擺線原理，將車床上固定的刀架通過齒輪組與車床主軸連接，使其能與車床主軸同向轉動，車刀刀尖在工件截面上形成內擺線的軌跡，可以近似地看作是正多邊形截面，該方法實現了連續加工，但由于其成型運動是回轉運動，刀尖運動所形成的截面必然是曲邊多邊形，與理想的多邊形截面存在誤差。

在誤差分析方面，已有對CA6140機床進行了改進的先例，由伺服電機直接驅動刀盤，并引入了編碼器對刀盤的轉速進行反饋控制，驗證了回轉車削多邊形軸類零件的原理正確性，但其直線度誤差較大，還有改進的空間[1-2]。也有從擺線方程入手的嘗試，分析各個參數對于擺線形態及擺線直線度誤差的影響，最終得到了一組合適的參數，通過仿真加工出截面形狀為正六邊形的軸，其直線度誤差0.018 mm[3]。由此可見，車床同向回轉加工多邊形截面軸類零件的原理是正確的，且其直線度誤差是能夠通過分析參數來進行優化。

本文通過建立平面直角坐標系，分析刀尖運動軌跡并建立刀尖軌跡方程。借助MATLAB建立刀尖的仿真軌跡，在軌跡方程中尋求兩回轉軸中心距與刀具回轉半徑的關系式，并通過該關系式得出加工出各正多邊形截面的直線度誤差不高于0.025 μm時所需要滿足的條件。

1 多邊形截面的車削成型原理

1.1 建立刀尖軌跡運動模型

兩個軸同時轉動并不方便建立坐標系進行軌跡分析，所以通過轉化運動，將工件軸中心作為基點，將刀具軸的運動視作一邊做自轉一邊圍繞基點做公轉的運動，這樣就能建立如圖1所示的平面直角坐標系，圖中：原點1是工件回轉中心、其轉速為1；2為刀具軸回轉中心、其轉速為2；轉速比可表示為＝2/1，即工件軸旋轉一圈、刀具軸旋轉圈；為工件在單位時間內轉動的角度，根據轉動方向不同，存在正負之分，此處規定工件逆時針轉動方向為正；為刀尖；為刀具軸與工件軸之間的中心距；為刀具的回轉半徑。根據該坐標系可以分析得出刀尖的運動軌跡及求得該軌跡的參數方程。

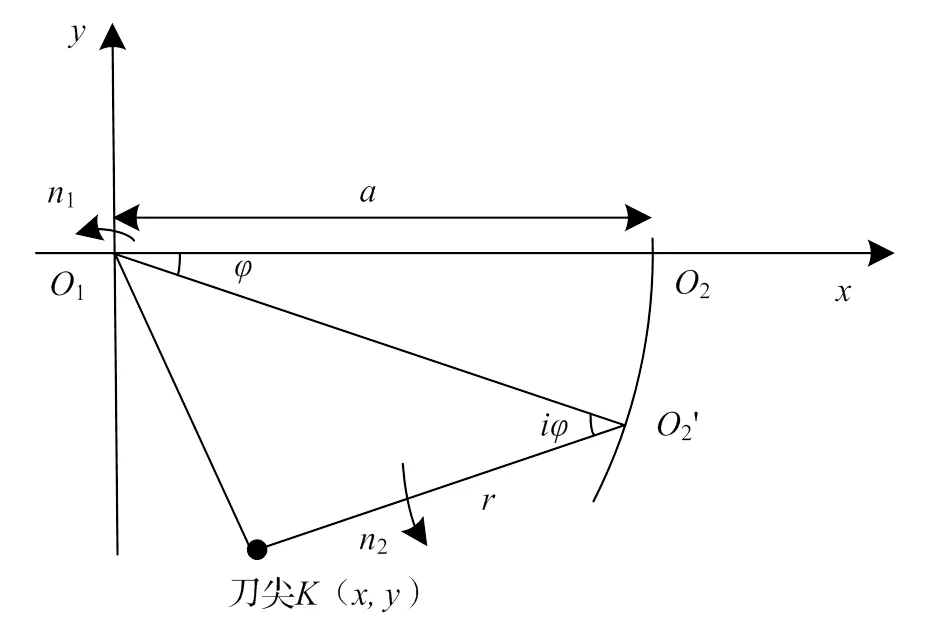
圖1 平面直角坐標系中的刀尖軌跡

根據建立的平面直角坐標系可以得出刀尖的移動軌跡是內擺線。內擺線的形成原理是一個小圓內切一個大圓，且小圓繞大圓做無滑動的滾動，繞大圓滾動一周后，小圓上的一點所形成的軌跡就是內擺線，內擺線的軌跡并不是固定的，而是隨著大圓和小圓的半徑比的變化而變化的[4]。

刀尖相對工件中心1運動的軌跡方程為：

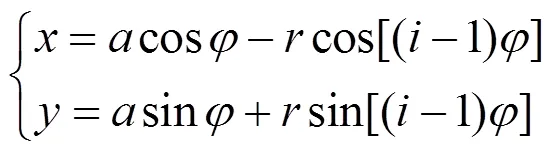
刀尖軌跡的幾何推導如圖2所示，在建立的平面直角坐標系（圖1）中添加三條輔助線：第一條以O2'為起點，做平行于O1O2的平行線，交y軸于點A，交O1K于點B；第二條仍然以O2'為起點，做垂直于x軸的垂線，交x軸于點D；第三條以K為起點，做垂直于AO2的垂線，交點為C。

根據幾何關系，可得到的已知條件有12'＝、∠12'＝。根據傳動關系，傳動比為，所以可得∠2'＝∠12'∠12'＝(1)。在△12'、△2'內運用三角函數可以求得線段2'、、1、2'的長度為2'＝sin、＝sin(1)、1＝cos、2'＝cos(1)。求出上述線段的長度后，根據幾何關系不難看出，點的縱坐標的絕對值是線段與2'的和、橫坐標的絕對值是線段1與2'的差，即：

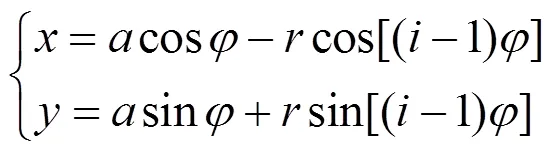
根據該軌跡方程能得出，刀尖轉動后形成的位移角為：

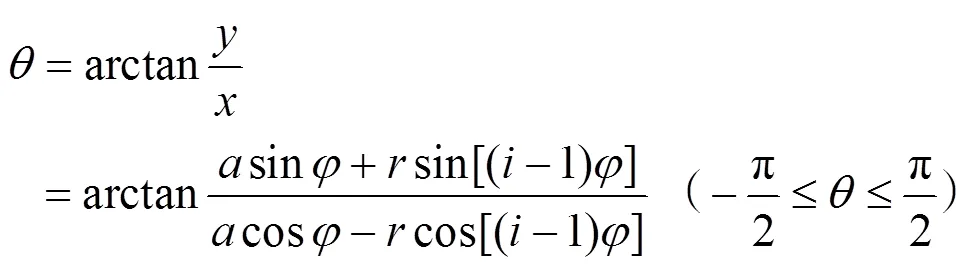
由此便得出了刀尖的運動軌跡以及參數方程，在理想情況下，只要回轉半徑足夠大，內擺線的每條邊都能視作是一條直線，也就實現了正多邊形截面軸的近似加工[5]。

1.2 機械傳動比方案與電子傳動比方案

多邊形截面軸的成型原理是將兩軸同向且轉速成比例旋轉時，刀尖所形成的內擺線軌跡看作是多邊形截面，傳統方法實現同向成比例轉速轉動的原理是通過齒輪組傳動實現的，一對齒輪嚙合會使連接齒輪的兩軸轉向相反，但只需要在帶動工件軸轉動的主動輪與帶動刀具軸轉動的從動輪之間增加一個齒輪，就能實現兩軸同軸轉動，而車床主軸和刀具軸之間的轉速比則可以根據三個齒輪之間的傳動比來確定，在需要改變傳動比時可以通過切換嚙合齒輪來改變傳動比關系（即換擋），但因為傳動比由齒輪齒數比決定，所以改變傳動比的范圍有限。

隨著數控技術的發展成熟，也有采用數控技術與反饋調節原理來實現同向成比例轉速轉動的方案，通過數控系統來同時控制工件軸和刀具軸的轉向和轉速，并引入反饋系統來實時監控調節兩軸的轉速比，將工件軸與刀具軸的轉速維持為一個恒定比值[6]。原理如圖3所示。

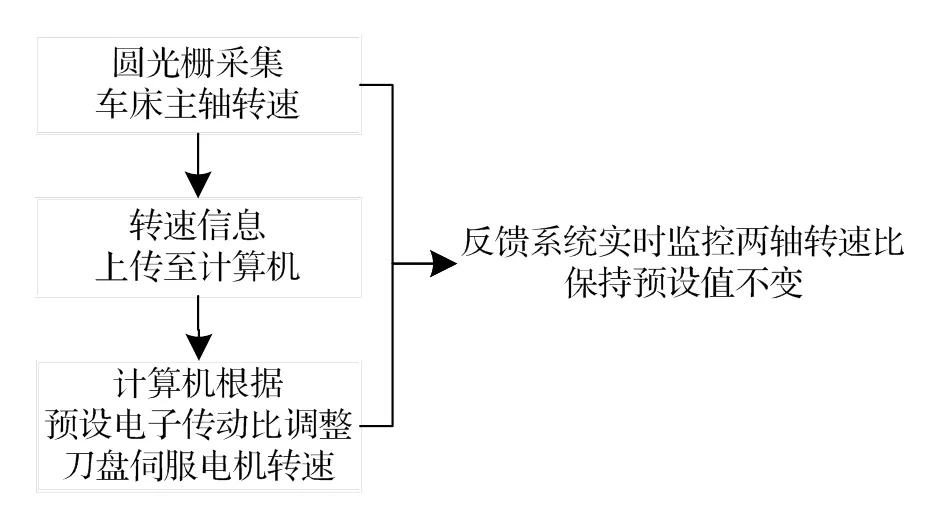
圖3 保持電子轉速比的流程

電子傳動比方案相比于機械傳動比方案，具有更高靈活性，調節傳動比范圍更大，可根據實際需求來進行調節，且改變傳動比時無需停車換擋，具有更高的加工效率與加工精度[7]。

2 MATLAB仿真刀尖軌跡

為了得到更加直觀的刀尖軌跡模型，在做參數分析之前運用MATLAB中的函數工具箱對刀尖形成的內擺線軌跡進行仿真。這也是最常用的將工程問題轉化為數學模型來進行分析求解的思路，數學模型仿真具有更好的可靠性，對于快速求解、求得最優解都有極大的幫助。

采用MATLAB求解刀尖軌跡時用到的數學模型即上文分析得出的刀尖軌跡方程式（1）。為分析得到具體軌跡，此次仿真采用MATLAB自帶函數工具箱中的ezplot函數，該函數能夠根據給出的函數關系式自動繪制出函數的軌跡，無需給出具體的定義域。

根據ezplot函數，輸入如下程序：

S=ezplot(‘x=acosθ-rcos[(i-1)θ]’,‘y=asinθ+rsin[(i-1)θ]’,[0,2*pi])

Set(S,'color','k')

規定工件轉角的取值范圍為0～2π，即工件轉動一周時刀尖運動形成的軌跡，式中、、都可以根據實際加工時的需求來給定具體數值。圖4是截面形狀分別為三角形與正六邊形的仿真圖形。

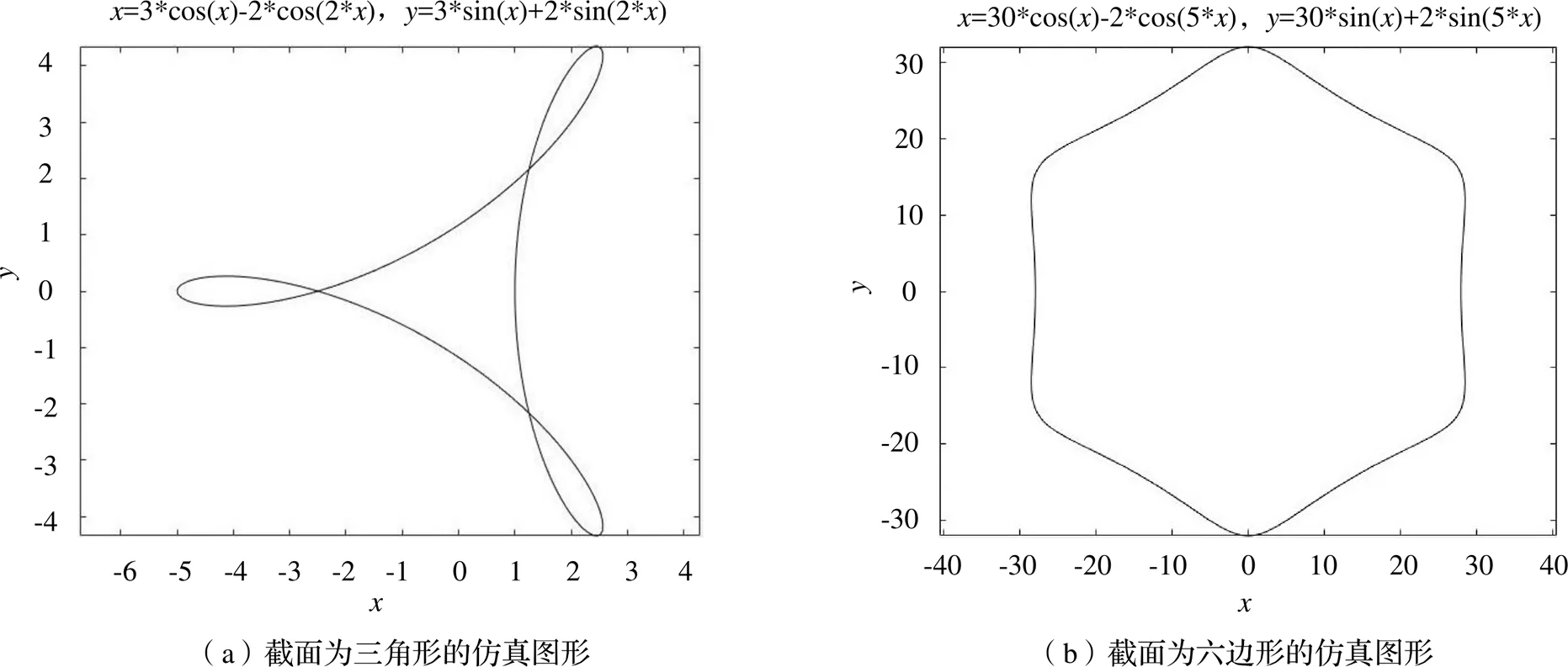
圖4 不同截面的仿真圖形

另外，當中心距和回轉半徑二者比值一定時，無論二者數值如何變化，內擺線軌跡是保持不變的，如果能夠找到一個合適的比值讓刀尖形成的內擺線軌跡每條邊的直線度誤差符合要求，那么則能夠根據這一比值與實際加工場合來對中心距和回轉半徑進行調整。同時通過刀具沿工件軸線移動即可成形截面為多邊形的平面。

3 多邊形截面直線度誤差分析

3.1 多邊形截面直線度誤差計算[8]

根據內擺線的成型原理以及具體的軌跡參數方程可以得出：當刀具的回轉半徑越小，就會使得內擺線的每一條邊的凹陷程度越大，所以在特定參數條件下，可以將內擺線的每一條邊的曲率半徑增加到足夠大，就能將內擺線的每一條邊都近似地認為是直線，內擺線就能近似地看作是一個正多邊形，但這樣的近似思想便會使正多邊形軸截面的每條邊產生直線度誤差，進而影響到每個面的平面度誤差。

誤差分析的原理如圖5所示。可知，刀尖通過加工形成的實際軌跡是一個凹邊內擺線，它與理想情況下的正多邊形是存在誤差的，取其中一條邊進行分析，建立了如圖所示的平面直角坐標系，使曲線關于軸對稱，弧和直線分別與軸有一個交點，令其分別為和，那么顯而易見的是，線段的長度就是實際軌跡和理想軌跡之間的加工誤差了，分析得出這樣的結果后，問題便轉化成了通過幾何關系求出線段的長度。

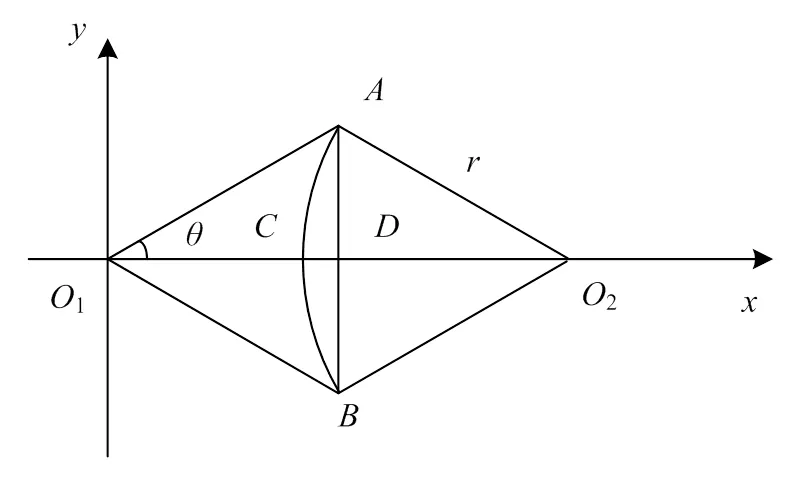
圖5 截面誤差示意圖

誤差計算以正六邊形為例，圖5中的點和點是成型截面中的頂點，設工件軸逆時針轉動為正方向轉動，那么刀尖在點時的位移角∠12＝，由正多邊形的幾何性質可知＝π/（為正多邊形的邊數），結合軌跡分析時得到的結論可知：

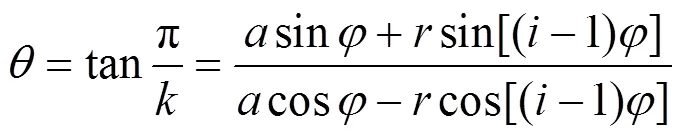
展開可得到：

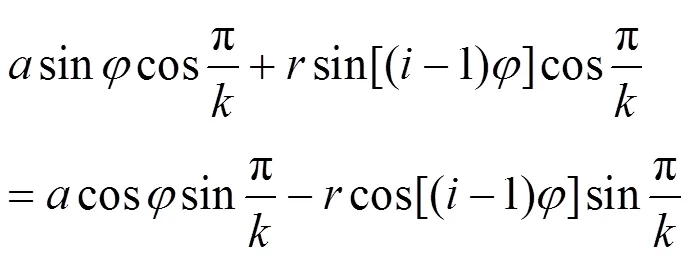
式（5）調整位置化簡后，可以代入輔助角公式再化簡得到：

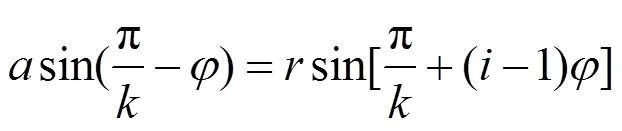
在圖1中，對△12'、邊12'、與邊2'使用正弦定理可得：

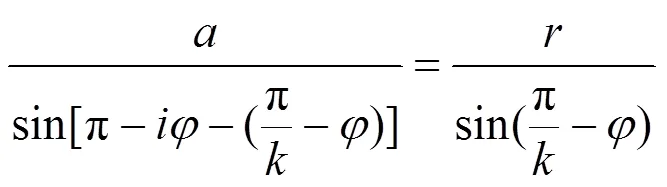
由于式（7）同時存在的加工邊數和轉速比之間存在聯系，根據傳動關系可知，當刀具軸上均勻裝夾了把車刀，刀具軸與工件軸的轉速比為（為整數）時，所形成的軸截面邊數＝×，故當刀具軸上只裝夾一把車刀時，截面邊數和轉速比在數值上相等，化簡式（7）可得：

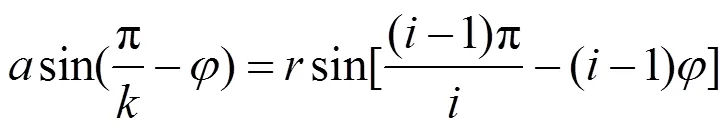
聯立式（6）（8）可以得到：

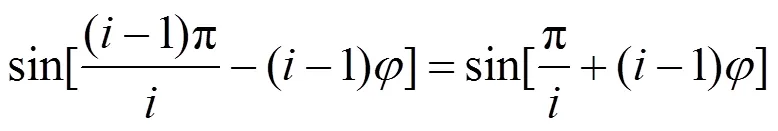
求解可得：

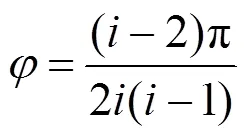
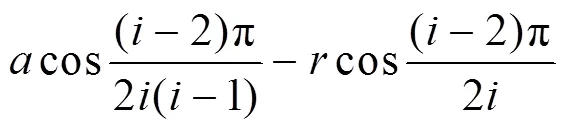
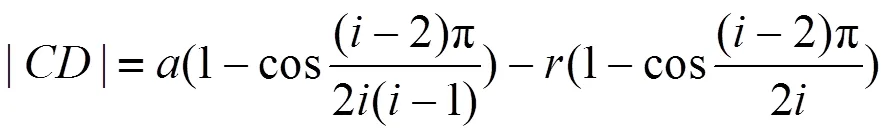
由式（10）可知：正多邊形截面的誤差由兩軸中心距、刀具回轉半徑、轉速比共同決定；兩軸中心距與誤差呈正相關，兩軸中心距越大、則誤差越大；而刀具回轉半徑與誤差呈負相關，刀具回轉半徑越小、形成的曲面越凹、自然平面度誤差也就越大[9]；而由于本方案只采用一把車刀加工，所以轉速比由實際的加工生產方案中的加工邊數來決定，代入生產中常用的加工邊數，即可獲得對應的兩軸中心距和刀具回轉半徑的代數關系如下：

加工正三角形截面軸時，＝3，則有：

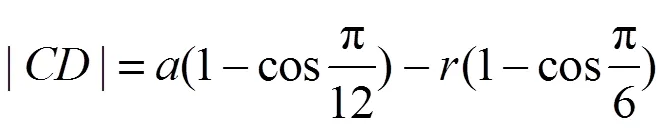
加工正方形截面軸時，＝4，則有：

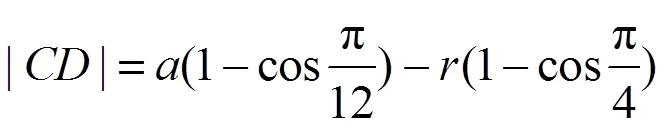
加工正五邊形截面軸時，＝5，則有：

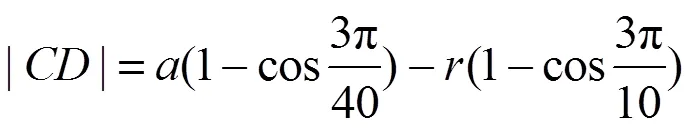
加工正六邊形截面軸時，＝6，則有：

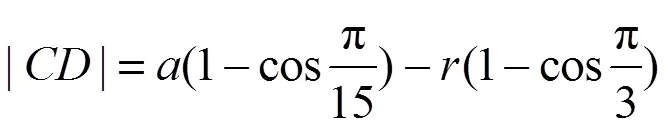
式（12）～（15）即為加工邊數不同時所形成的不同誤差與兩軸中心距和刀具回轉半徑的關系式，在實際加工中可以通過調整兩軸中心距和刀具回轉半徑來控制誤差的大小。

而在前文中的MATLAB仿真分析軌跡時提到過，截面的凹凸程度與兩軸中心距及刀具回轉半徑的比值有關，即當兩軸中心距和刀具回轉半徑的比值發生變化時，成型截面的誤差也會發生變化，下面將對其進行分析。

在理想情況下，加工得到的截面形狀恰好是正多邊形，即此時的||為零，但由于加工中的各項因素，導致加工誤差必定是存在的，如果將加工誤差近似地看作為零，即可得到相應的關系式如下：

加工正三角形截面軸時，令||≥0，則有：

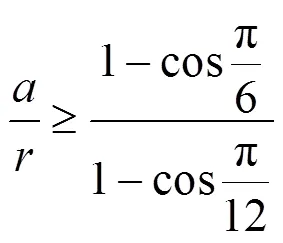
加工正方形截面軸時，令||≥0，則有：

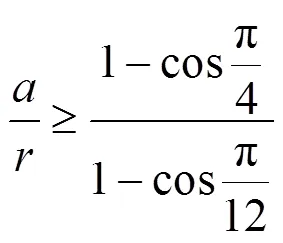
加工正五邊形截面軸時，令||≥0，則有：

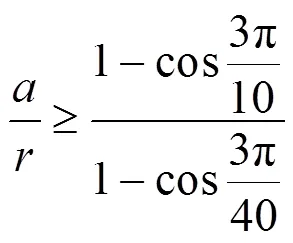
加工正六邊形截面軸時，令||≥0，則有：

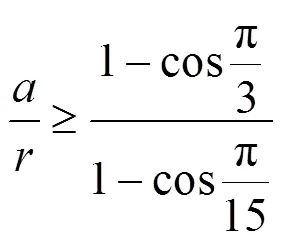
這樣就得到了將誤差近似看作0時初步得到的兩軸中心距和刀具回轉半徑的比值，其他情況都是理想條件下時，盡量滿足對應邊數的比值，得到的誤差會是一個比較滿意的結果。在實際生產中，車間可根據這樣的比值，結合加工零件的實際尺寸來調整兩軸中心距及刀具回轉半徑，進而減小加工誤差，提高加工精度。

3.2 多邊形截面直線度誤差驗算

前文得出了加工時為了得到較好的直線度誤差所需要滿足的中心距與回轉半徑的比值關系，由于其關系式內存在余弦函數，故其比值為無限不循環小數，取臨界值的本質是向臨界無限靠近，所以小數點后的位數取得越多，截面的直線度誤差就越小。

下面將以正六邊形截面為例說明，驗算該關系能否使直線度誤差達到0.025 μm。

正六邊形截面直線度誤差為||＝(1－cos(π/15))－(1－cos(π/3))，中心距與回轉半徑的比值為（1－cos(π/3)）/（1－cos(π/15)），將余弦值小數點位數取到后六位時，比值為22.8812，回轉半徑同樣取10 mm、12.5 mm、15 mm及20 mm，直線度誤差如表1所示，可得當余弦值取到小數點后六位時，獲得的直線度誤差符合≤0.025 μm的要求，即在實際加工中，保持這一比值來對中心距與回轉半徑進行調整，就能加工出符合直線度要求的截面。而在實際加工中，當刀具的主偏角和副偏角為零時，通過刀具沿工件軸線水平移動即可將軸截面的直線度轉化為整根軸的平面度，從而可得到軸上多邊形平面度誤差≤0.025 μm[10]。

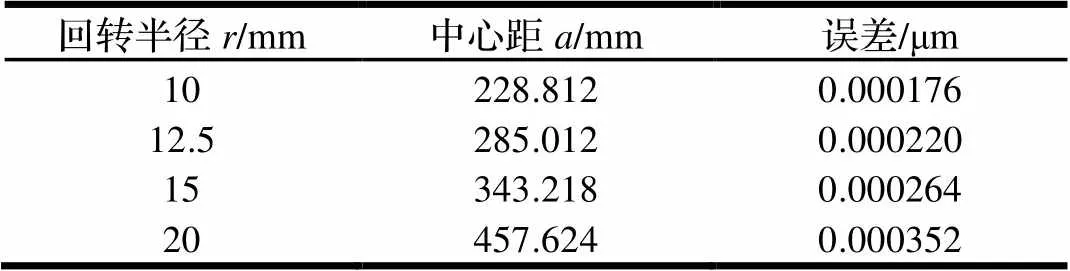
表1 中心距與回轉半徑比值為22.8812時的直線度誤差

4 MATLAB仿真檢驗

前文得出了中心距和回轉半徑的比值，滿足直線度誤差不超過0.025 μm得到加工截面邊數和對應的比值如表2所示。

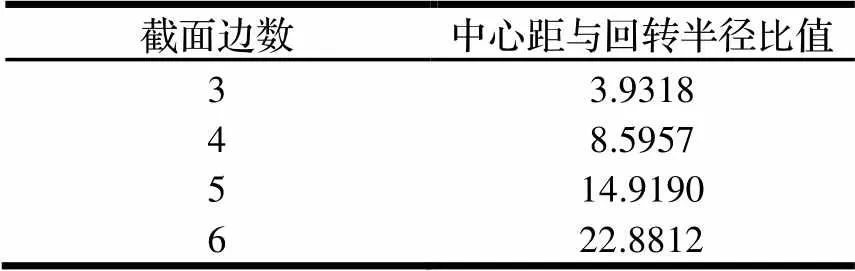
表2 截面邊數與對應的比值

仍以三角形與六邊形截面為例，運用MATLAB軟件對表2陳列的比值結果進行仿真檢驗，如圖6所示，可以看出，截面的曲邊得到了較好的修整，且原本容易產生應力集中的尖角也被轉化為圓角，在一定程度上有助于提高軸的使用壽命[11]。

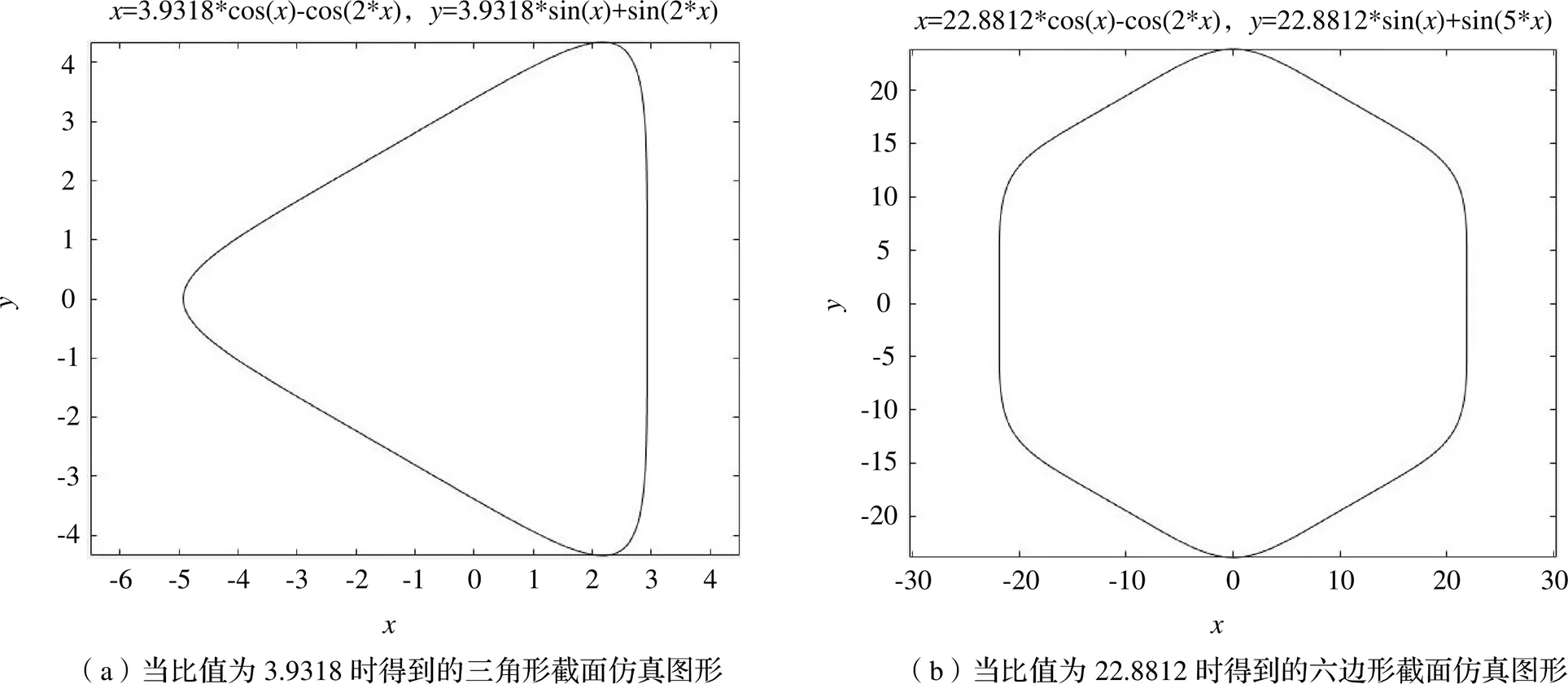
圖6 成特定比例的不同截面仿真圖形

5 結論

本文從對多邊形截面軸的成型原理入手，對該類軸的誤差進行了來源分析及優化計算，得出了如下結論：

（1）電子齒輪傳動方案在大部分場合下具有比機械齒輪傳動方案更大的選擇范圍、更高的加工效率及加工精度。

（2）兩軸間的中心距和刀具的回轉半徑比值是影響截面內擺線軌跡曲邊直線度誤差的主要因素，當兩者比值發生改變后，內擺線軌跡直線度誤差發生變化。

（3）對于不同邊數的截面而言，當中心距和回轉半徑成一定比例時，內擺線軌跡的曲邊直線度誤差能夠得到優化。

[1]趙韓，徐林森，吳焱明，等. 固定輪系的旋輪線及在車削多面體中的應用[J]. 農業機械學報，2006（11）：125-128.

[2]趙韓，徐林森，吳焱明，等. 車削多面體運動的矢量建模及誤差分析[J]. 農業機械學報，2007（4）：154-157.

[3]葛秀光，李佳，王麗萍，等. 擺線在多邊形零件加工中的應用[J]. 機床與液壓，2005（2）：45-47.

[4]Sung L. M.，Tsai Y. C.. A study on the mathematical models and contact ratios of extended cycloid and cycloid bevel gear sets[J]. Mechanism and Machine Theory，1997，32（1）：39-50.

[5]汪諍. 內擺線原理和車方機床分析[J]. 蘭州交通大學學報，2010，29（4）：119-121.

[6]韓紹民，趙慶志，劉世忠，等. 數控機床電子齒輪傳動比計算方法及其機械性能研究[J]. 裝備制造技術，2014（3）：34-36.

[7]王義朋. 數控車方機床的加工和發展趨勢研究[J]. 現代制造技術與裝備，2018（6）：159-160.

[8]胡昌軍，錢瑞明，馮淑慧. 回轉車床上的正多面體零件加工及誤差分析[J]. 輕工機械，2008，26（6）：4.

[9]扈傳云，吳亞瑾. 端部為正多邊形的軸類零件的加工[J]. 機械工程師，2001（7）：42.

[10]鄧中亮．非圓零件車削加工技術[M]. 1版. 北京：人民郵電出版社，1998.

[11]《機械設計手冊》聯合編寫組. 機械設計手冊[M]. 北京：化學工業出版社，1982.

Working Principle and Error Analysis of CNC Lathe for Polygonal Shaft Parts Based on Electronic Transmission Ratio

NI Mingwei，LUO Hongbo

( School of Mechanical Engineering,Sichuan University, Chengdu 610065, China )

Polygonal shaft parts have the characteristics of keyless connection and are widely used in many transmission scenarios, but the traditional machining methods have the disadvantages of low accuracy and low efficiency. In recent years, a method of turning polygon axes with two axes turning in the same direction has been proposed. This paper aims to reduce the flatness error of turning polygon axes on CNC lathes. Based on the molding principle of polygon axis, the geometric model of the tool tip trajectory was established and the trajectory equation of the tool tip was analyzed. The simulation trajectory of the polygon axis section with different number of edges was obtained by substituting the trajectory equation of the tool tip into MATLAB. After geometric analysis of the simulation trajectory, the expression of the section straightness error is obtained, that is, the machining error can be obtained by adjusting the machining parameters in the actual machining. According to the above methods, the machining parameters required by different edge shapes to meet the flatness error (not more than 0.025 μm) of the project were finally obtained.

electronic transmission ratio；polygon axis；error analysis；the MATLAB simulation

TH16；TH114

A

10.3969/j.issn.1006-0316.2022.10.002

1006-0316 (2022) 10-0008-07

2021-03-24

四川省科技計劃重點研發項目（2021YFG0188）；2017-2018四川省科技廳重點研發項目“基于電子傳動比的多邊形軸類零件復合數控車床”（2021YFG0188）

倪明威（1999－），四川成都人，主要研究方向為機械制造，E-mail：1284607302@qq.com；羅紅波（1963－），四川成都人，工學碩士，副教授、碩士生導師，主要研究方向為數控機床、機械結構設計，E-mail：lhuuo630@126.com。