扭旋角度對新型靜態混合器混合性能的影響

李星宇，張春梅，楊鵬達

（沈陽化工大學 機械與動力工程學院，遼寧 沈陽 110142）

SK型靜態混合器是一種傳統的靜態混合器，可適用于石油化工、精細化工、生物石油加工等領域的攪拌、反應、提純、傳熱等流程。國內外學者對SK型靜態混合器的混合特性開展了廣泛的研究,得到了許多重要的結論。孟輝波等[1-2]進行了 SK型靜態混合器的湍流流動數值模擬，揭示了 SK型靜態混合器切割區內部流動阻力特性和混沌運動特性，為了提高 SK型靜態混合器的性能，一些學者對其結構進行了改進，設計了新型靜態混合器；Hobbs等[3]在低雷諾數條件下，對Kenics 型靜態混合器進行了模擬研究，得出改變扭旋元件的長徑比時，能夠影響靜態混合器的混合效率；龔斌等[4]對多葉片的靜態混合器內的流場進行了分析，發現靜態混合器內有強弱漩渦，強化徑向混合；王宗勇等[5]對多流道螺旋靜態混合器的混合性能進行了研究，得出流道的增加能夠增強流體混合效率、縮短混合元件長度。本文在 SK型靜態混合器結構的基礎上，結合多流道的思想，提出一種新型的靜態混合器，利用Fluent進行數值模擬仿真，改變扭旋角度時，對該靜態混合器混合性能的影響進行研究。

1 研究對象及方法

1.1 新型混合器的幾何結構

本文研究的靜態混合器由一根主管、一根支管、四個混合元件組成，如圖1所示。

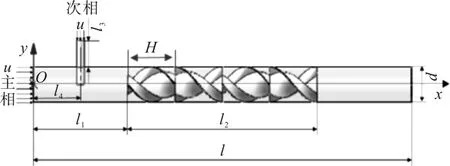
圖1 靜態混合器結構示意圖

在混合管內SK形混合元件和扭旋片同心布置，中心1/2直徑處為SK型混合元件，外圍1/4直徑為關于原點呈中心對稱的夾角β=90°的扭旋片組成，扭旋片長度為H，扭旋角為α，相鄰兩個混合元件中左旋螺旋板和右旋螺旋板在管內呈錯開90°交替排布，如圖2所示,靜態混合器的主要幾何結構參數如表1。

圖2 靜態混合器元件的幾何模型（α=180°）

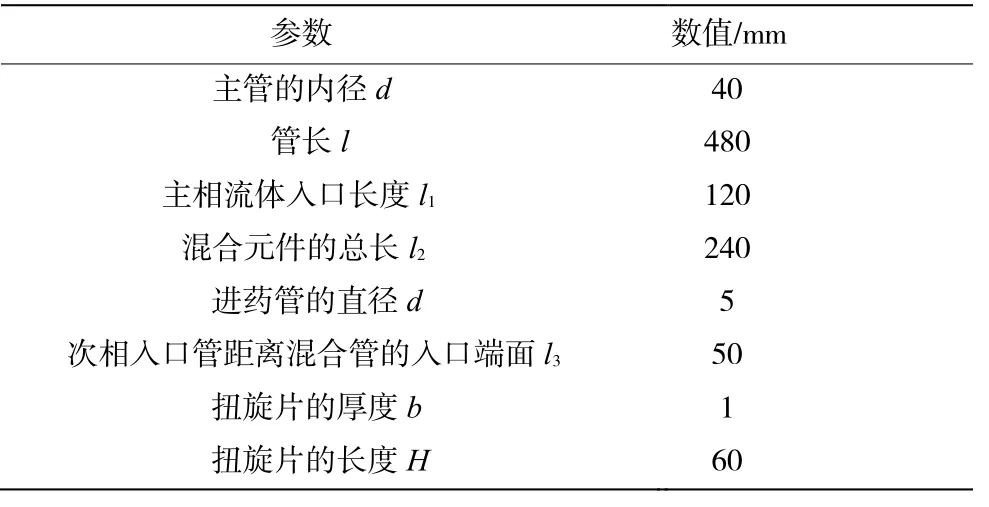
表1 靜態混合器的幾何尺寸

1.2 模擬方案

模型使用Solidworks進行建模,使用Fluent對靜態混合器內的流體濃度場進行數值模擬。模擬研究的主相采用20 ℃水（密度為998.2 kg·m-3，黏度為0.001 003 Pa·s），次相為H2SO4（密度為1 836 kg·m-3，黏度為0.010 18 Pa·s）；兩種流體均為連續的不可壓縮的牛頓流體，忽略重力的影響。多流模型采用mixture[7]模型。設定主相流動方向為X軸正方向，建立如圖1的坐標系。 假設所有物性參數都是定值,主相與次相的入口速度相同，采用均勻速度的入口邊界，出口邊界條件選用自由出流。壓力與速度耦合選擇SIMPLC算法。

靜態混合器內的流體流動狀態利用主相入口的雷諾數Re為參照，由雷諾數計算公式（1）可得主相的入口速度。

式中：ρ—流體密度，kg·m-3；

u—入口流體速度，m·s-1；

d—入口內徑，mm；

μ—流體動力黏度，Pa·s。

1.3 網格無關性檢驗

在對研究對象進行網格劃分時，如果網格劃分數量過大，造成計算量太大，收斂速率低，而網格劃分數量過少時，可能達不到所需計算精度，為此，根據流體流過最后一個混合元件的分離強度I確定合適的網格數量。

分離強度為流體的實際濃度方差與尚未混合時的方差的比值，表達式如（2）。

式中：X—對某一截面內H2SO4的m個采樣點的體積分數平均值；

Xi—某一截面中不同位置H2SO4的體積分數。

在主相的入口雷諾數Re=1 200的情況下，對α=150°靜態混合器內濃度場模擬計算, 所得流體流過最后一個混合元件的分離強度隨網格密度變動情況如圖3所示。在圖中, 可發現網格總量在2 188 474以后的變化起伏明顯降低, 變化不超過5%, 亦即當網格總數超過2 188 474之后,分離強度就基本不再改變, 而此時的網格總量也不再影響運算準確度,故本文選擇網格數在2 188 474以上進行模擬計算。

圖3 分離強度隨網格數量變化曲線

2 混合性能

在主相的入口雷若數Re=1 200的情況下，對α=90°、120°、150°、180°四種混合器內濃度場進行數值模擬。

2.1 軸向濃度分布

不同扭旋角對應的靜態混合器軸向截面 H2SO4濃度分布云圖，如圖4所示。

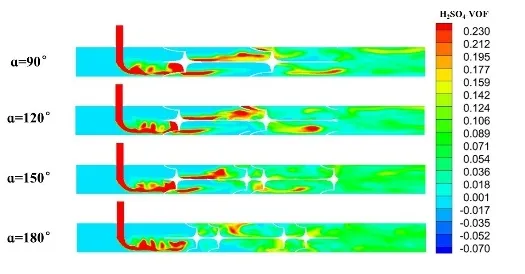
圖4 混合器軸向截面的H2SO4體積分數分布云圖

由圖4可以看到兩種流體在第一段混合元件混合前兩種流體幾乎尚未混合，經過第一個混合元件后，混合區域開始逐漸擴大。流體經過4個混合元件扭旋作用基本都能達到均勻混合的效果。混合元件能夠加速混合過程，使流體加速擴散過程。當扭旋角從90°增大到180°，可以明顯看到混合元件的混合能力隨著扭旋角的增大而增強，扭旋角為180°時，能夠在最少的混合元件的條件下達到相同的混合效果。

2.2 徑向濃度分布

不同扭轉角度在每個扭轉元件的首尾徑向H2SO4的的體積分數分布云圖如圖5所示。

圖5 徑向H2SO4體積分數分布云圖

從圖5可以看到，x=120 mm截面次相即使通過加藥管匯入主流管道中，在混合元件前的管內幾乎沒有發生混合。在經過第一個混合元件后，可以觀察到x=180 mm截面的兩流體開始出種現交錯，說明兩種流體開始在混合元件的扭旋作用下被分割成多個區域。x=240 mm截面的次相混合更加均勻，混合的效果明顯改善，此時將混合效果進行比較可以發現，α=90°和α=120°下仍存在高濃度區域，故混合效果相對較差。在流體到達的x=300 mm時，α=180°的混合元件使得流體基本混合均勻，α=90°仍存在部分高濃度區域，α=120°和α=150°混合效果相差不大，說明扭旋角度的增加改善了混合速度。在最后一個元件的出口截面, 除了α=90°之外, 其他混合器徑向H2SO4體積分數基本均勻。

2.3 混合特性定量分析

為了進一步地定量分析靜態混合器的混合效果，通過采用分離強度來說明混合的均勻程度[8-9]。由式（2）計算得出混合器內元件進出口位置的分離強度。

不同扭角的混合器內特征軸向位置分離強度對比如圖6所示。

圖6 分離強度隨軸向位置的變化關系

由圖6可以發現流體在經過第一個混合元件后，α=180°混合器的分離強度值迅速降低到0.11，混合效果非常顯著，而α=90°的混合器則需要兩個混合元件才能達到相同的分離強度。流體流經α=120°的混合器三個混合元件時，分離強度為0.0573，而α=180°只需要流經兩個混合元件就能達到同樣的分離強度值，相同條件下節省一個混合元件。α=150°的混合器與α=180°的混合器經過對比，經過第一個混合元件的分離強度值大于α=180°，即α=180°的混合器混合效果更好，第一個混合元件后混合性能相差不大；總之，α在 90°～180°時，混合效果隨著扭轉角度的增大而增大。

通過利用貢獻率，進一步說明每一段混合元件對整個混合器混合效果的貢獻程度[10]。貢獻率表達式如下：

式中：Ii,m—第m個元件在入口截面的分離強度；

Io,m—第m個元件在出口截面的分離強度；

m—第m個混合元件。

根據式（3）可以計算得到四個混合元件的貢獻率分別是 57%、24%、13%、6%。濃度相比主相較低的次相在第一個混合元件扭旋的作用下，便與主相充分混合，分離強度下降明顯。隨著第二個混合元件的繼續作用，前三個混合元件對全部混合效果貢獻超過90%。第四個混合元件對混合效應的貢獻較低, 而且分離強度隨軸向位移的變動較平緩,說明此時混合元件不再提升混合性能，而是起維持混合狀態的作用。說明提高本文這種新型靜態混合器的混合性能的有效途徑為增大前三個元件的混合性能，可采用增加扭旋角的辦法來實現。

3 結 論

在低雷諾數情況下，本文所提出的新型靜態混合器內，扭旋角為 180°的混合器經過前三個混合元件的作用，混合效果明顯優于其余三者。兩相流體混合速度隨扭旋角增大而增大，濃度分布更均勻；扭旋角的增大使得混合分離強度的降低速率增大，混合性能更優。適當地提高扭旋角參數有利于提高該靜態混合器的混合性能。