基于干擾觀測器的四旋翼吊掛系統非線性控制

趙永生，陳欣宇，范云生

(大連海事大學船舶電氣工程學院，遼寧 大連 116026)

1 引言

近年來，由于飛行器起降方便，移動不受地形影響等特點[1，2]，越來越多的研究人員從事飛行器的開發研究工作，飛行器的使用也越來越普及，多使用于航拍領域如影視拍攝、新聞報道、電力巡檢、環境監測等使用攝像機的領域[3]，因此世界海關組織協調制度委員會(HSC)將之歸類為“會飛的照相機”。隨著飛行器的發展，開始出現飛行器吊掛負載的應用，吊掛運輸在快遞運輸及危險地區救援等方面均有突出表現[4，5]。如何控制四旋翼飛行器吊掛系統成為新的研究熱點[6]。

四旋翼飛行器吊掛系統是一個多自由度、強耦合、欠驅動的復雜系統，控制難度很大[7]。其增加的兩個擺角自由度加劇了系統的耦合程度，使系統的控制難度大大提升，尤其吊掛擺角不能直接控制，需通過飛行器位置來間接控制，并且易受外界甚至飛行器旋翼旋轉產生的風的干擾影響，進而破壞整個吊掛系統的穩定。

許多學者對四旋翼吊掛系統進行了深入研究。文獻[8]用能量分析的方法設計了四旋翼無人機吊掛飛行系統的非線性控制器，在抑制吊掛物擺動的同時飛行器也能到達目標位置。文獻[9]將系統模型轉換為開環結構的有限時間差分博弈問題，與納什均衡解和滾動優化的思想相結合，設計了基于狀態反饋的滾動納什控制器。文獻[10]通過動態反饋將系統轉化為線性能控系統，并設計了動態反饋控制律。文獻[11]將四旋翼吊掛系統建立為差速混合動力系統，設計了非線性控制器，使飛行器姿態及負載姿態控制器全局指數穩定。文獻[12]對負載質量變化的情況設計了魯棒滑模控制器(SMC)，可快速跟蹤所需軌跡，同時抑制抖動。文獻[13]引入虛擬力用于位置控制，使用反步法四旋翼姿態控制和負載擺角控制將實際推力驅動到該虛擬力，從而實現軌跡跟蹤。

當前的研究已經較為完善，但仍存在一些不足之處，體現在未對吊掛負載設計控制器，對吊掛負載所受干擾考慮不夠充分，僅利用控制器的魯棒性減小干擾影響。

結合前人經驗，本文對上述問題進行了優化[14-19]。首先為吊掛負載設計控制器，將其對飛行器的整體干擾轉化為對飛行器位置的干擾，不影響飛行器的姿態響應；其次針對吊掛負載易受干擾問題設計了干擾觀測器估計所受干擾并修正；最后設計了四旋翼吊掛實驗平臺驗證設計方案。文章結構如下：第一部分運用牛頓-歐拉及拉格朗日方法[23]建立四旋翼吊掛系統的數學模型；第二部分針對吊掛負載干擾問題設計干擾觀測器觀測負載所受干擾并返回修正；第三部分為四旋翼吊掛系統姿態、位置及擺角三部分的控制器設計；第四部分為實驗平臺的搭建及驗證。

2 數學模型的建立

四旋翼吊掛系統有四個輸入、八個自由度，是一個高度耦合、高度欠驅動的復雜系統，不能簡單將吊掛負載當作干擾處理，需要在傳統四旋翼飛行器模型的基礎上建立新的四旋翼吊掛系統模型，其示意圖如下：

圖1為建立的四旋翼吊掛系統示意圖，其中飛行器為常見十字形四旋翼飛行器。以飛行器質心點為原點o建立坐標系，給出各參數定義如下：飛行器前后方向為X軸方向且后退為負，左右方向為Y軸方向且向右為正，上下方向為Z軸方向且向上為正；飛行器繞X軸旋轉角度為橫滾角φ且向右轉動為正，飛行器繞Y軸旋轉角度為俯仰角θ且向下轉動為正，飛行器繞Z軸旋轉角度為偏航角ψ且向右轉動為正。α擺角為吊掛繩與飛行器xoz平面夾角，β擺角為吊掛繩與飛行器yoz平面夾角，L為吊掛繩索長度。令四旋翼質心到電機軸心長度為l，飛行器質量為M，負載質量為m。在對四旋翼吊掛系統進行建模時，由于系統較復雜、模型不確定性等因素的影響，需對模型做出一些簡化：忽略空氣阻力對飛行器吊掛系統的影響，認為吊掛繩是剛性的且質量不計，吊掛繩的懸掛點為飛行器質心。

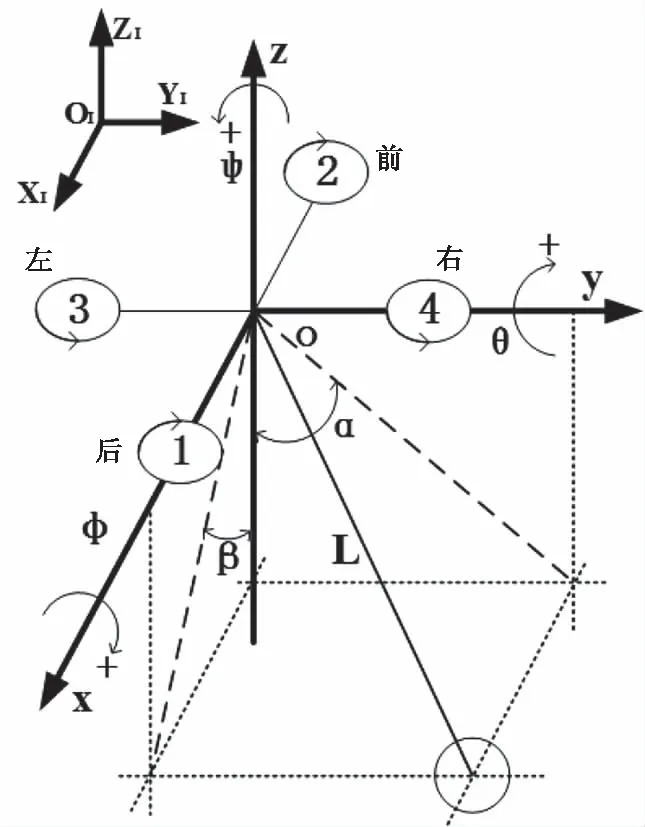
圖1 四旋翼吊掛系統模型

傳統四旋翼飛行器數學模型為

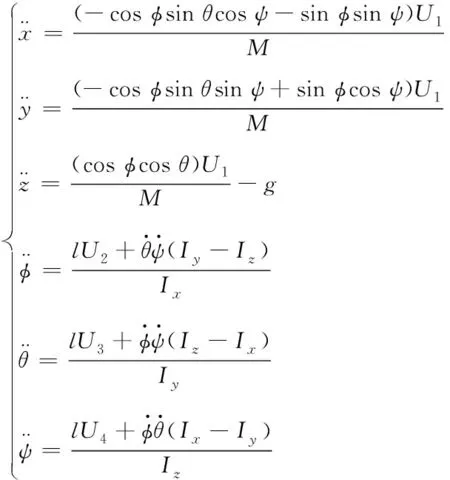
(1)

其中，U1代表四個旋翼產生的總升力，U2代表橫滾力，U3代表俯仰力，U4代表偏航力矩。g代表重力加速度，Ix、Iy、Iz代表機體繞相應坐標軸的轉動慣量。

在傳統四旋翼飛行器的基礎上，四旋翼吊掛系統增加了吊掛物，通過對四旋翼及吊掛物進行受力分析來建立四旋翼吊掛系統的數學模型。

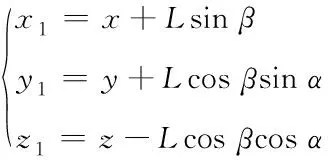
(2)

對其兩邊進行二階求導，即可得吊掛物加速度與四旋翼飛行器加速度之間的關系

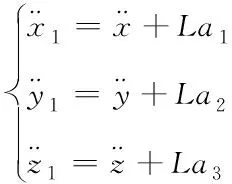
(3)

且

由加速度關系式可對其進行受力分析

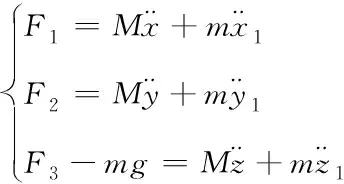
(4)

將式(1)和式(3)代入式(4)，得：

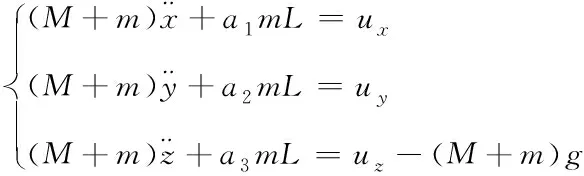
(5)

采用哈密爾頓原理及拉格朗日公式計算系統總動能

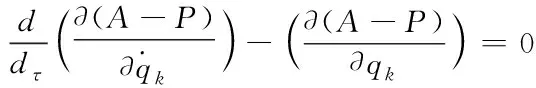
(6)

A為四旋翼吊掛系統總動能，P為系統勢能，系統總動能A為

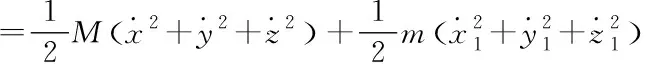
(7)

認為地平面是零勢能，可得系統的勢能P為

P=(M+m)gz-mgLcosβcosα

(8)

得到系統總動能及勢能后，將其代入拉格朗日公式，qk取α和β，計算后可得吊掛物擺角加速度與四旋翼飛行器加速度之間的關系式

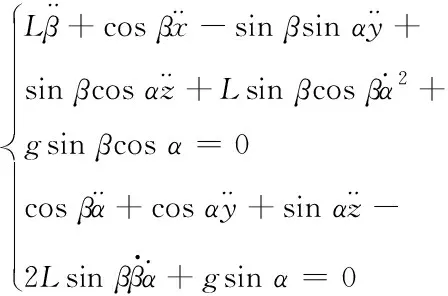
(9)

由式(1)、(5)、(9)得八自由度的四旋翼吊掛系統數學模型

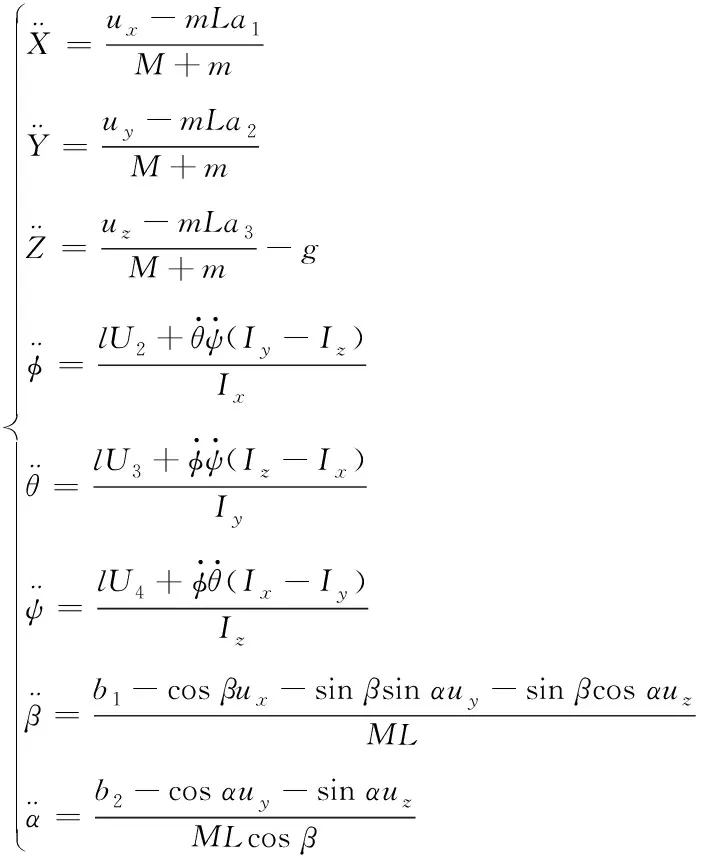
(10)

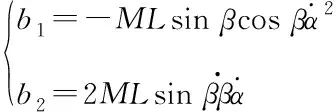
由式(10)可知，吊掛物的擺角加速度與四旋翼飛行器的加速度相互耦合，吊掛物的擺動會影響飛行器的穩定，而飛行器的移動又會影響吊掛物的擺動。因此需分別對吊掛物擺角及飛行器位置設計控制器，并且吊掛物易受各類外界干擾影響，為其設計干擾觀測器以修正干擾影響。

3 干擾觀測器的設計

吊掛物擺角為四旋翼吊掛系統欠驅動程度最深的部分，并由于其懸掛運輸方式，極易受到外界風干擾、飛行器螺旋槳轉動產生的風干擾及飛行器本身震動的干擾，因此需設計干擾觀測器對吊掛物擺角所受干擾進行估計和修正。以吊掛物擺角β為例設計擺角干擾觀測器。

在式(10)的擺角數學模型中加入模型不確定性及外界干擾力矩影響，得到新的數學模型如下

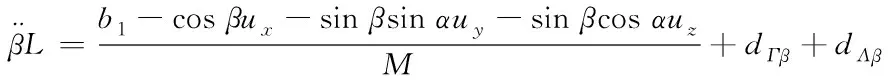
(11)

其中dΓβ表示模型不確定性，dΛβ表示外界干擾，模型總干擾為

dβ=dΓβ+dΛβ

(12)

由式(10)、(12)得系統擺角新的數學模型

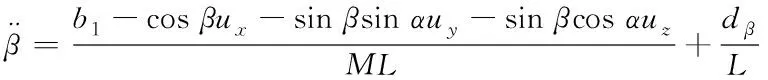
(13)

將式(13)寫作仿射非線性系統格式

x=f(x)+g1(x)u+g2(x)d

(14)

得

(15)

為提高系統的魯棒性，需對干擾dβ進行補償，設計非線性干擾觀測器對干擾dβ進行觀測

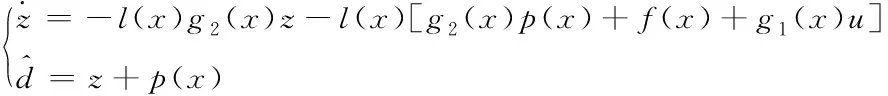
(16)

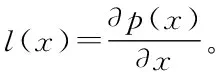
設計吊掛物β擺角的干擾觀測器如下

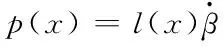
(17)

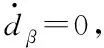
由此可以得到誤差導數為

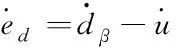
(18)

由式(17)、(18)得

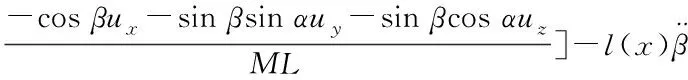
(19)

代入式(13)

=l(x)u＿dβ/L-l(x)dβ/L

=-l(x)ed/L

(20)

由式(20)可知，選取合適的l(x)可使系統漸進穩定，隨時間變化擾動估計誤差將趨于零。

同理可得吊掛物α擺角干擾觀測器

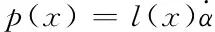
(21)

4 控制器的設計

四旋翼吊掛系統為四輸入、八輸出的強耦合欠驅動系統，并且多個變量均易受干擾，因此需要設計干擾觀測器對干擾進行估計和補償，并為每個自由度設計控制器來控制。其控制部分可分為四個子系統：可直接驅動的高度及偏航子系統，內環控制的姿態子系統，外環控制的飛行器位置子系統，外環控制的吊掛物擺角子系統。其控制流程圖如下

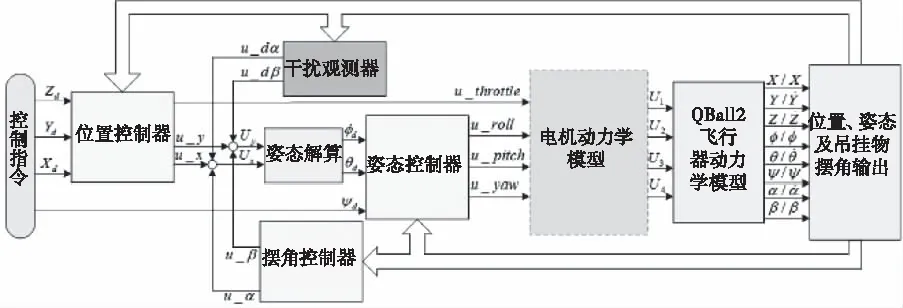
圖2 四旋翼吊掛系統控制流程

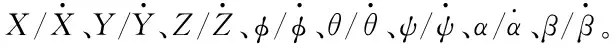
飛行器橫滾角和姿態角對飛行器的位置影響較小，因此將其忽略作小角度近似，得位置-姿態轉換公式如下

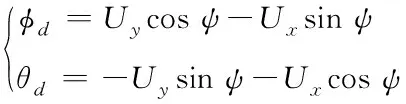
(22)

及電機模型轉換公式如下

(23)

Kt、Ky為升力系數和反扭矩系數。

4.1 位置控制器設計

四旋翼吊掛系統的位置控制器、姿態控制器及擺角控制器均采用積分型反步法控制器。相比于傳統的反步法，積分型反步法在消除靜態誤差、減小模型不確定性以及外界影響方面有優勢。

以四旋翼吊掛系統飛行器高度通道為例設計控制器，高度期望值Zd與實際值Z的差為

z1=Zd-Z

(24)

對式(24)求導，得其跟蹤誤差的導數

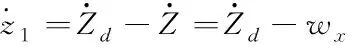
(25)

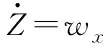
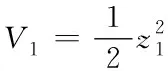
(26)

對其求導，得

(27)

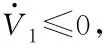
(28)

在虛擬控制量后加入了積分項，可增強控制器的魯棒性、消除模型不確定性的影響

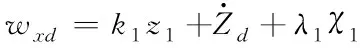
(29)

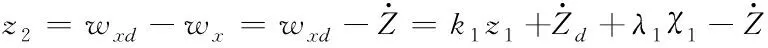
(30)

代入式(27)，得

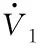
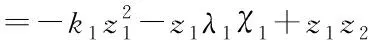
(31)

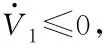
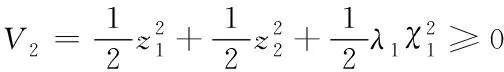
(32)

對式(30)求導

(33)

將飛行器高度數學模型式(10)代入式(33)

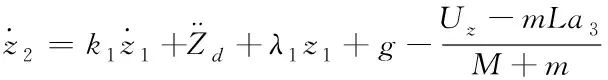
(34)

則

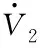
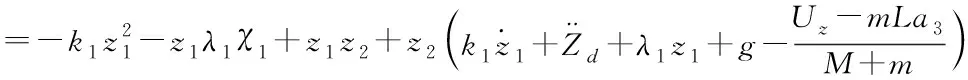
(35)

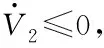
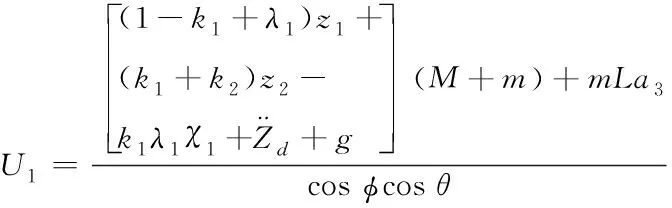
(36)

式中，k2為大于0常數。將式(36)代入式(35)，得

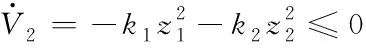
(37)

由式(32)(37)可證明所設計的控制律令高度漸進穩定。

同理可得飛行器位置控制器的控制律

(38)

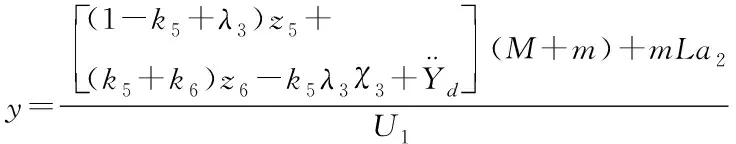
(39)

其中kn(n=3…6)、λi(i=2，3)為大于0常數，且

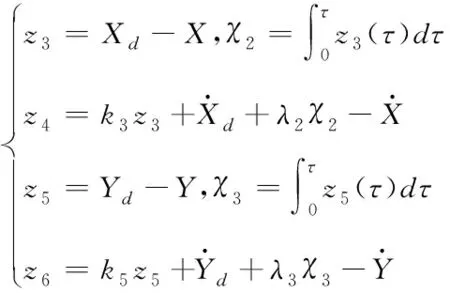
(40)

4.2 吊掛物擺角控制器

吊掛物擺角由于其欠驅動的特性，無法直接控制，需通過控制器將其轉化為位置信號間接控制。控制器采用積分型反步法控制器，設計方法與上文類似，故省略詳細過程，得

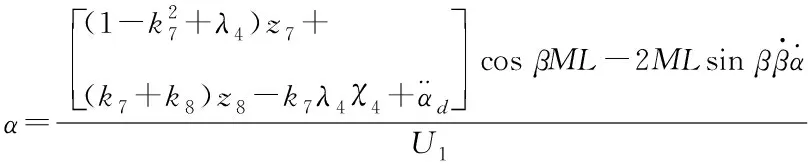
(41)

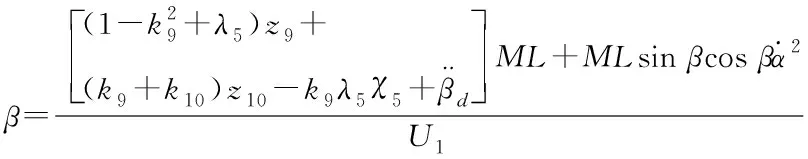
(42)

其中kn(n=7…10)、λi(i=4，5)為大于0常數，且

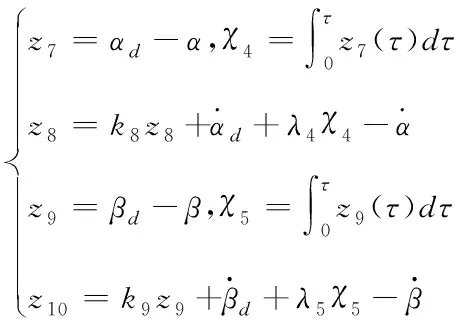
(43)

由式(38)、(39)得到飛行器位置控制器控制量和式(41)、(42)得到的吊掛物擺角控制量及式(17)、(21)得到干擾觀測器的補償量，可得四旋翼吊掛系統的飛行器位置控制量

(44)

4.3 姿態控制器

得到飛行器位置控制量后，經式(22)將其轉化為姿態角控制量。飛行器姿態角控制為系統的內環控制，采用積分型反步法控制，方法同上，在此僅給出結果

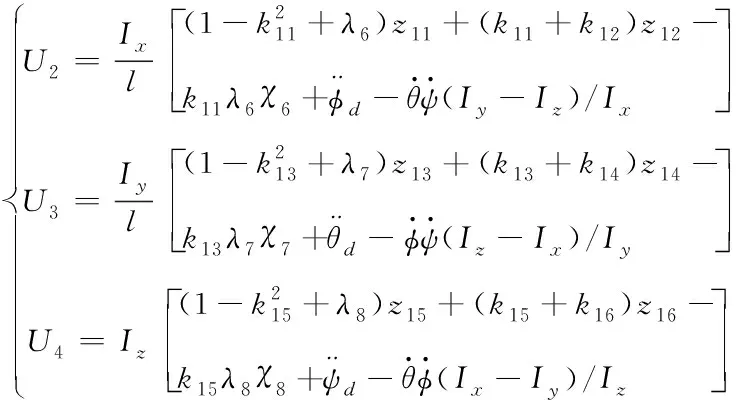
(45)

其中kn(n=11…16)、λi(i=6，7，8)為大于0常數，且

(46)

5 仿真驗證

仿真在MATLAB/Simulink中運行，四旋翼飛行器采用Quanser公司生產的QBall2的參數，吊掛負載為0.2kg重心為中心的圓球，吊掛繩長1.5m，系統參數如表1。

表1 模型參數

由圖3-5可知，吊掛物的擺動會影響四旋翼飛行器的穩定性，尤其對飛行器位置影響較大，積分型反步法可以有效降低擺動帶來的干擾。

圖3 飛行器高度變化

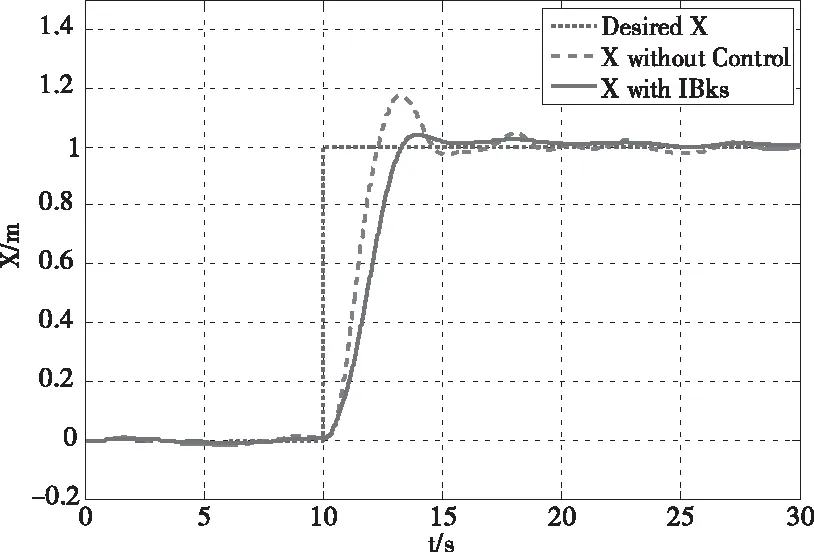
圖4 飛行器X位置變化

圖5 飛行器Y位置變化

由圖6、7可知，在沒有擺角控制器的時候，吊掛物會產生較大的擺角，不利于吊掛系統的穩定，而加入擺角控制器后可以將擺角降到較小的值，且可快速穩定。

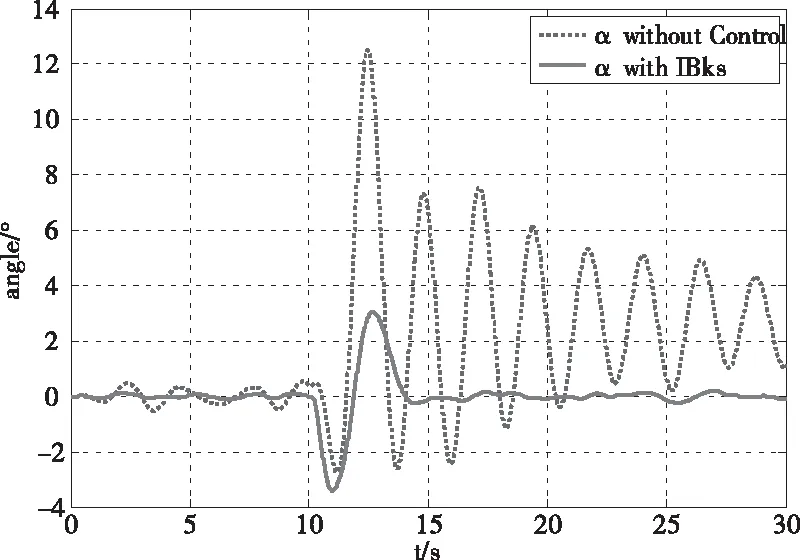
圖6 吊掛α擺角變化

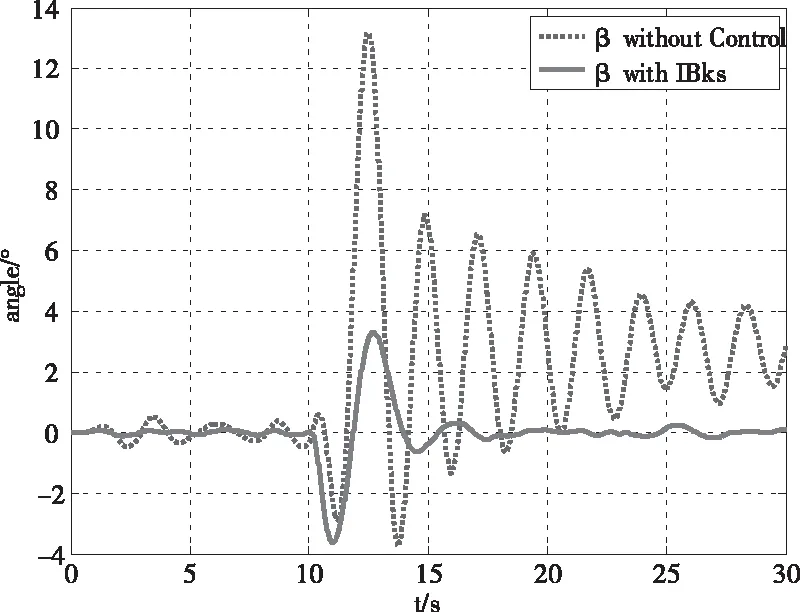
圖7 吊掛β擺角變化

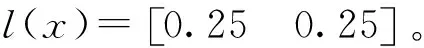
由圖8、9可知，在受干擾影響后，不加入干擾觀測器時吊掛擺角會出現較大的震動，不利于系統的穩定，而加入干擾觀測器可以有效地降低干擾的影響。由圖10可知干擾觀測器不僅能觀測出加入的干擾，同時還能觀測出飛行器移動對吊掛擺角帶來的干擾。

圖8 吊掛α擺角DOBC下變化

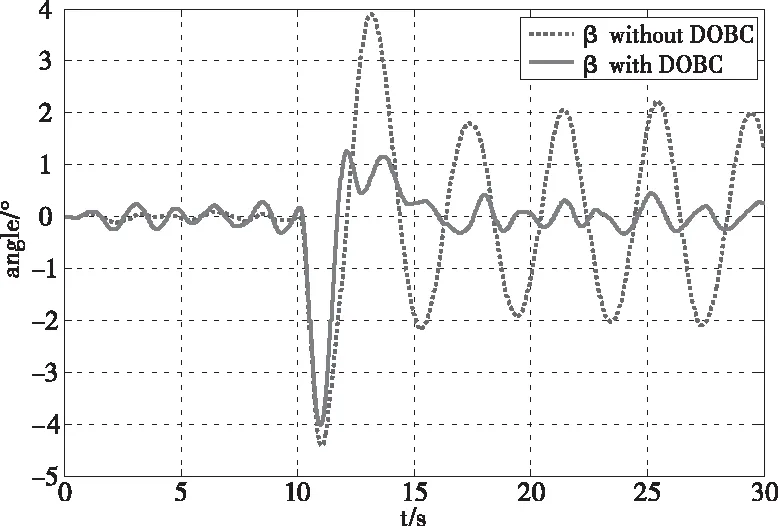
圖9 吊掛β擺角DOBC下變化

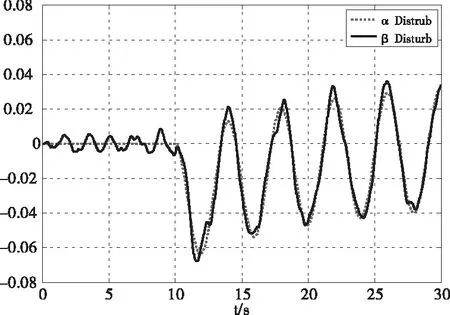
圖10 干擾觀測器觀測的干擾

圖11-14為飛行器姿態及電機相關量，從中可知飛行器在飛行過程中各項參數均處于正常范圍內，證明了該系統的可行性。

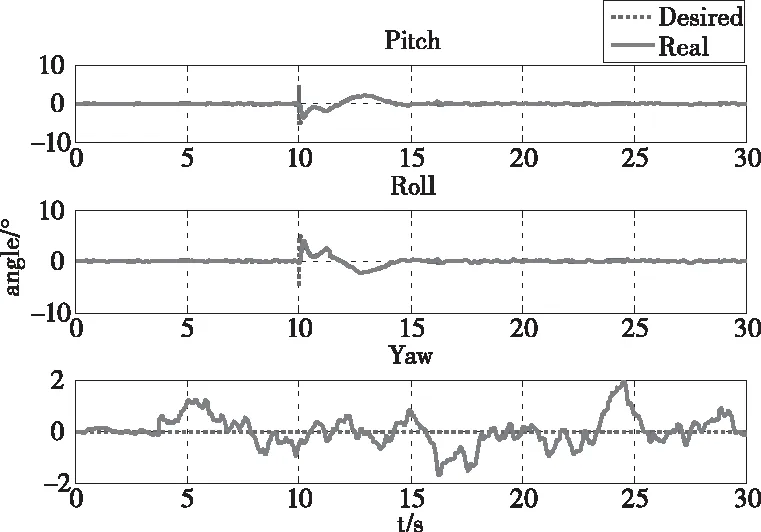
圖11 飛行器姿態角變化

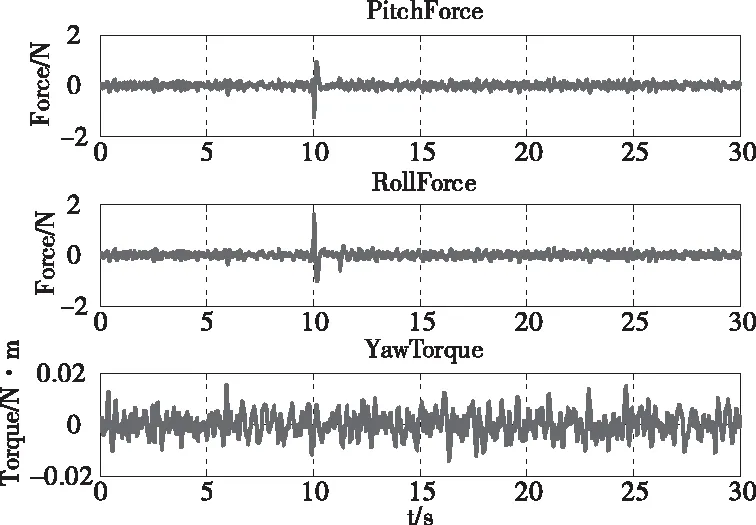
圖12 飛行器姿態力矩變化

圖13 飛行器姿態控制量變化

圖14 電機PWM控制信號

6 結論

本文主要針對四旋翼吊掛系統的吊掛物擺動問題。首先為系統建立了數學模型，然后為飛行器位置、姿態及吊掛物擺角設計了積分型反步法控制器，并針對吊掛物易受干擾的情況設計了擺角干擾觀測器對干擾進行估計和補償。最后在MATLAB/Simulink中搭建仿真模型對搭建的數學模型及控制器、觀測器進行驗證，仿真表明設計的非線性控制器可以有效降低吊掛物擺動對飛行器造成的影響，同時設計的干擾觀測器能觀測出外界干擾的影響并補償，可增強系統的魯棒性，降低干擾帶來的誤差，對四旋翼吊掛飛行運輸帶來一種有效可行的方案。