高應變率下含水紅砂巖爆破損傷演化模型研究

柴耀光，劉連生,2，曾 鵬，劉 偉，易文華，楊 硯，鐘抒亮,陶鐵軍,3

(1.江西理工大學資源與環境工程學院，江西 贛州 341000; 2.江西省礦業工程重點實驗室，江西 贛州 341000; 3.貴州大學土木工程學院，貴陽 550000)

近年來，爆破技術因其高效性而被廣泛應用于礦山開采、隧道開挖、地下工程等領域[1-2]。得益于此，地下工程及開采作業逐漸向深部進行。自然條件下，巖體大多處于含水狀態[3]，巖體的力學性能受水的影響很大，含水量的微小變化可能會導致巖石強度與變形能力的顯著變化。地下工程爆破開挖時，不可避免的會遇到含水巖體，輕易忽略爆破沖擊對含水巖體的損傷影響，可能會引發重大安全事故。因此，為探究含水巖體在爆破沖擊作用下的損傷演化規律，有必要建立相應的損傷本構方程。

國內外學者[4-9]研究發現，既使是巖性不同的巖樣，其力學特性也往往隨著含水率的升高而逐漸劣化：巖石顆粒與水之間的水-巖交互作用受礦物組成、粒徑、孔隙體積等結構的影響較大，不同巖石類型之間差異較明顯。損傷本構模型作為描述巖石破壞過程的有效工具而被眾多學者[10-12]所推崇，與此同時，考慮復雜載荷或環境條件下的巖石靜載損傷模型已經引起了許多研究人員[13-16]的注意，并取得了豐富的研究成果。在此基礎上Li等[17]、Qiao等[18]、Dong等[19]、Suzuki等[20]對于巖石動態本構方程也進行了詳細的探究，王聰聰等[21]基于斷裂力學建立了含水裂紋在爆破擾動下的力學模型。然而，卻很少有研究涉及含水率和應變率耦合作用下巖石的動態損傷本構方程。含水紅砂巖在動載作用下其損傷可以分為兩部分：一是水對巖體力學性能的劣化引起的宏觀損傷；二是動荷載沖擊對巖體內部裂隙等所造成的微觀損傷；因此可從宏觀與微觀兩方面探究其動載作用下所受復合損傷。針對不同含水率的紅砂巖試樣，巖石內部損傷隨著含水率的增加而逐漸擴大，表現為巖體彈性模量、內摩擦角、粘聚力等參數的降低，其中巖體彈性模量常用來表征巖體的損傷[22-23]。因此考慮用彈性模量定義紅砂巖的含水損傷；荷載作用下，巖體內部微元破壞數量與其所受荷載大小呈正相關關系，可用微元體破壞數量來定義荷載損傷。為了準確描述含水率和應變率耦合作用下巖石的本構方程，本文考慮將巖石損傷等效為兩部分：不同含水率造成的宏觀損傷以及不同應變率作用導致的微觀損傷，進而提出一個可以綜合反映含水率和應變率耦合作用下的紅砂巖動態損傷本構方程。

本文通過對含水紅砂巖進行動態沖擊試驗。基于Weibull分布與Drucker-Prager準則，推導得到紅砂巖在含水率與應變率耦合作用下的復合損傷變量與動態損傷本構方程，并將本構方程推導的理論曲線與試驗所得進行對比，擬合度較好。

1 試驗

1.1 試樣制備

試驗所用紅砂巖由江西贛州采集，由石英、長石、云母等礦物組成。按ISRM[24]建議，切割成直徑50 mm長徑比1∶1的圓柱體。通過測量試樣孔隙度、質量、縱波波速等，剔除離散性較大試樣。將制備好的紅砂巖置于實驗室通風1個月，得到完全干燥試樣。部分制備好的試樣如圖1所示。

圖1 部分試樣

為得到不同含水率的試樣，將加工好的試樣置入盛滿水的水箱中，間隔1 h取出進行稱重，直到試樣重量不變為止，認為此時試樣已飽和。根據其重量的變化可確定試樣含水率，公式如下：

(1)

式中：ω為巖石含水率;Ww為含水巖石質量;Ws為干燥巖石質量。

經試驗，不同含水率的試樣可通過控制浸水時間得到。本試驗設計5種含水率，分別為0%、0.75%、1.5%、2.25%、3.0%。不同含水率試樣制備過程如表1所示。

表1 不同含水率試樣制備

1.2 儀器簡介

沖擊試驗在霍普金森壓桿[25]上進行。裝置沖頭與桿件由40 Cr合金鋼制成，密度為7 810 kg/m3; 縱波波速為5 400 m/s；彈性極限為800 MPa；入射桿、透射桿與緩沖桿的長度分別為2.0、1.5、0.5 m。為確保所得試驗數據的有效性，每次沖擊后進行動態應力平衡檢驗(見圖2)。直徑50 mm的SHPB試驗系統如圖3所示。

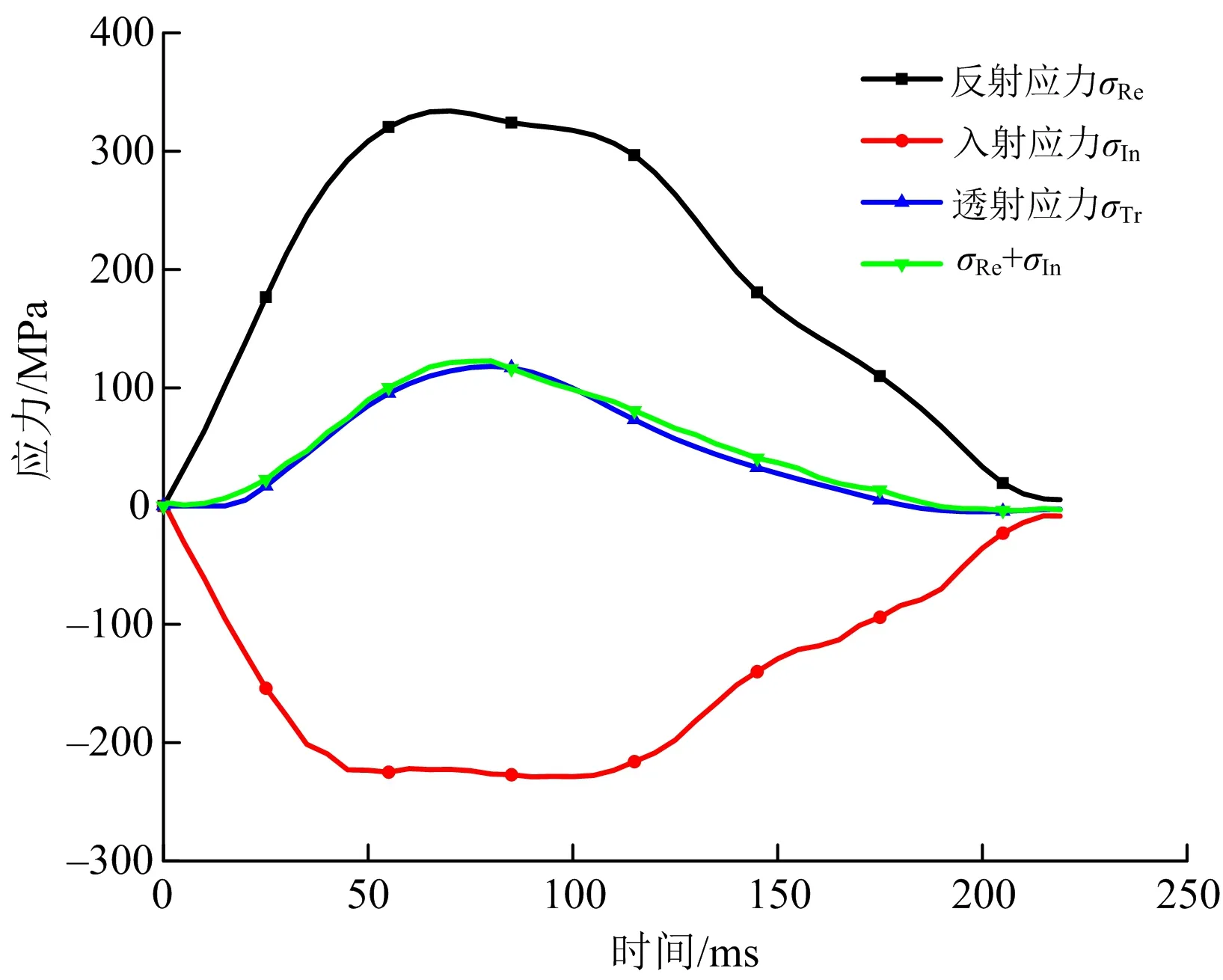
圖2 試樣N-5-5動態應力平衡

圖3 SHPB試驗系統

1.3 試驗方案

為探究高應變率下含水紅砂巖的復合損傷變量與動態損傷方程，試驗分設5種不同的含水率與應變率，對其組合分析。試驗分為5組，以N為編號，后接不同的數字組合進分組。以N-1-1為例，中間的數字范圍由1～5，代表了由低到高的5種應變率。而末尾的數字同樣由1～5，代表由低到高的5種含水率。每組試驗重復3次，由于數據過多，每組試驗僅列出1組試驗結果，部分試驗數據如表2所示，其變化規律如圖4所示。

表2 紅砂巖動態壓縮試驗結果

圖4 紅砂巖動態應力-應變

由圖4可知，隨著含水率的增加，試樣的動態彈性模量逐漸減小，峰值應力對應的破壞應變逐漸降低，臨界應變逐漸變大；試樣在破壞后，應力-應變曲線并非直線下降, 而是應力緩慢下降至臨界應變處后迅速破壞，即隨著含水率的增加，試樣逐漸由脆性向延性轉化。相同應變率下，試樣的峰值應力隨含水率的增加而降低。

2 紅砂巖損傷演化方程

2.1 含水狀態下紅砂巖損傷演化方程

本文所采用的損傷變量由宏觀與微觀兩部分組成，微觀損傷可由裂隙數目、缺陷體積等來定義；宏觀方面可以用波速、能量、密度、波阻抗、彈性模量等來定義；在含水率和應變率的共同影響下，巖石的損傷不僅表現在微觀結構上，而且在力學性能上也有不同程度的劣化。含水率越高，水對巖體所造成的宏觀損傷就會越大，彈性模量下降越多。因此可用彈性模量來定義巖體含水損傷，表達式為

(2)

式中：D1為含水率損傷變量；Eω為不同含水率巖石的彈性模量；E0為干燥狀態下巖石的彈性模量。

2.2 荷載作用下紅砂巖損傷演化方程

目前，正態分布與Weibull分布是最常用的2種巖石微元強度分布方式。第1種分布方式可以較好的描述巖石內部損傷的演化且物理意義較為明確，但是計算過程過于復雜，實際應用較少。第2種基于Weibull理論的分布方式卻具有計算量小、描述準確等優點，因此被更多的學者所采用。其表達式如下：

(3)

p(F)=0(F≤0)

(4)

式中：m、F0為Weibull分布參數。

巖體受荷時，其內部微元體破壞數量增加，當破壞數量達到極限時，會引起巖體的宏觀破壞。因此，荷載損傷變量可以用微元體破壞數量來衡量，即：

(5)

式中：D2為荷載作用損傷變量；Nn為已破壞的微元體數目；N為總的微元體數目。

當巖體所受外荷載由0增長到F時，其內部微元體破壞數目可由下式進行計算：

(6)

將式(6)代入式(5)，可求得荷載損傷變量：

(7)

微元體受荷時的損傷本構方程可根據等效應變假設求得：

(8)

從式(7)可以看出，荷載損傷變量D2與微元體的強度F有關。Drucker-Prager準則(以下簡稱D-P準則)因比其他理論更能反映巖體的實際情況而被廣泛應用。本文認為紅砂巖的破壞服從D-P準則[26-27]。

(9)

式中：φ為巖石的內摩擦角;I1 ,J2為應力張量的第一不變量和應力偏量的第二不變量。

基于D-P準則，曹文貴等[28]確定了在三軸壓縮條件下巖石的I1與J2的表達式：

(10)

(11)

式中：v為試樣的泊松比；E為試樣的初始彈性模量；ε1為試樣的軸向應變。

動態單軸壓縮下，試樣的σ2=σ3=0，ε1=ε。式(10)、式(11)可轉化為

I1=Eε

(12)

(13)

把式(12)、式(13)代入式(9)中可得：

(14)

對式(8)、式(14)求導可得：

(15)

(16)

當試樣的應變達到臨界應變，即ε=εf時，由函數在極值點處導數為零可得：

(17)

聯立式(15)、式(16)、式(17)可得：

(18)

(19)

巖石在臨界破壞即ε=εf時，σ=σf，此時把式(19)代入式(8)中可得：

(20)

把式(20)代入式(7)，可得巖石受荷載作用時的損傷變量表達式：

(21)

2.3 復合損傷變量的演化方程

含水率以及荷載作用均會對巖石試樣產生不同的損傷，根據損傷力學理論，巖石的損傷變量可以用宏觀物理指標如彈性模量表示。表達式如下：

(22)

式中：Dω為復合損傷變量;Eω為含水率和荷載作用下巖石彈性模量;E0為初始彈性模量。

巖石在單軸加載下的應力-應變關系可根據等效應變原理求得，如下：

(23)

式中：σ,E為未損壞材料的應力和彈性模量；σ*,E*為損壞材料的有效應力和相應的彈性模量；ε,D分別為材料的應變和損傷變量。

巖石在含水率與荷載共同作用下的本構關系如下：

σ=E0(1-Dω)ε

(24)

式(24)中Dω可表述為

Dω=D1+D2-D1D2

(25)

從式(25)可知，巖體的整體損傷變量Dω由含水損傷D1和荷載損傷D2以及它們之間的耦合相互作用組成。因此，損傷變量呈現典型的非線性特征。此外，由于耦合項整體為負，說明含水率和應變率的耦合效應實際上削弱了巖石的總體損傷。

綜上，單軸壓縮下含水巖體的損傷本構方程為

σ=E0[1-(D1+D2-D1D2)]ε

(26)

上述所說荷載損傷為靜態荷載下巖石的損傷,對于動態壓縮下，由于巖石率效應的影響，試樣所受的應變率越大，其彈性模量、臨界應變就會越來越大。考慮到應變率的影響，將荷載損傷變量D2看作為應變率有關量，即D2中的參數均視為應變率相關量。從式(21)可以看出，與荷載損傷變量有關的巖石宏觀物理指標有峰值應力、臨界應變和彈性模量，因此動態壓縮下巖石荷載損傷變量D2的計算方式是以干燥紅砂巖試樣的動態壓縮試驗為基礎，根據試驗所得的不同應變率下的峰值應力、臨界應變、彈性模量等參數，繪制出相應的散點圖并進行擬合，進而得到巖石宏觀物理參數的率效應模型，并將其與含水損傷變量共同代入式(25)可得到含水率和應變率共同作用下的復合損傷變量。

3 損傷變量的確定

3.1 含水損傷變量

D1可由含水紅砂巖的靜態彈性模量代入式(2)求得，計算結果如表3所示，變化規律如圖5所示。

表3 D1隨含水率的變化規律

圖5 D1隨含水率變化

D1整體的變化近似呈指數函數增長。方程如下：

D1=-0.709e(-ω/3.113)+0.706 (R2=0.99)

(27)

由圖5可知，D1隨含水率的增加而逐漸增大。這是因為隨著巖體內部水分增加，更多的巖體開始遭受水巖作用，造成的損傷逐漸變大。由曲線斜率可知，D1增長的趨勢逐漸減小，這是由于隨著水分不斷進入試樣內部，試樣逐漸飽和，水-巖耦合作用逐漸達到平衡，損傷的增加也在逐漸減小。

3.2 荷載損傷變量

根據式(20)，在含水率為0的情況下，選取不同應變率下的損傷變量來計算所需的彈性模量、峰值應力等參數,用于計算荷載損傷的m值。得應變率作用下m的變化曲線(見圖6)。由圖6可以看出，m與應變率兩者之間近似呈線性關系，m隨著應變率的增加而逐漸增大，表達式如下：

圖6 m值隨應變率變化

(28)

把計算好的m值代入到式(21)中可得荷載損傷D2隨應變的變化曲線(見圖7)。

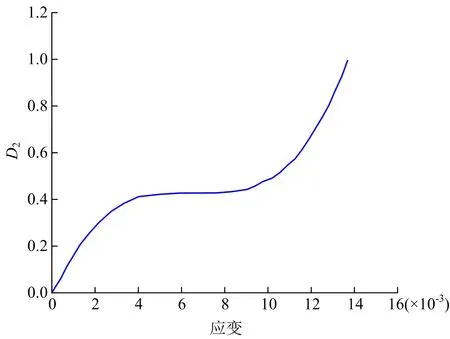
圖7 D2隨應變變化

由圖7可知，沖擊作用下，荷載損傷D2的增長過程可分為3部分，即初始階段、低速發展階段和快速發展階段。初始階段，巖體瞬間遭受動荷載作用，內部孔隙、裂紋等閉合，荷載損傷量迅速增加，并隨著應變率的增加而擴大。但此階段作用于巖體上的應變率，并不足以使巖體內部產生新的裂紋，所以其荷載損傷量趨于穩定。對應于巖石動態壓縮過程中的壓密階段；低速發展階段，荷載損傷增長幾乎為0，對應于巖石壓縮過程中的彈性階段與微裂紋穩定擴展階段，此階段裂紋增加緩慢，損傷變量變化較小；快速發展階段，損傷快速增長，對應于巖石裂紋快速擴展與破壞階段，巖石內部產生大量裂隙，并迅速貫通，損傷快速增加，直至巖石完全破壞。

3.3 復合損傷變量

根據得到的含水損傷變量D1和荷載損傷變量D2的變化規律，計算D1、D2的值并代入式(25)中，可以得到含水率和應變率共同影響下的復合損傷變量Dω的變化趨勢。應變率為96.93 s-1時，不同含水率下復合損傷Dω的變化如圖8所示。

圖8 Dω隨應變變化

由圖8可知，復合損傷變量Dω與荷載損傷D2的變化趨勢近似，不同的是在中期復合損傷變量Dω的變化相較于荷載損傷D2較為緩和。這是由于在裂紋加速擴展階段，由于水Stefan效應[29]的影響，會阻止裂紋的快速擴展，進而導致復合損傷Dω在加速階段的變化較為緩和。

由圖8可知，當應變為0時，此時的復合損傷變量Dω僅代表含水損傷。且含水率越大時，Dω的初值越大，巖石的初始含水損傷越嚴重。

4 紅砂巖動態損傷本構模型驗證

為驗證理論推導所得紅砂巖動態損傷本構模型的準確性，將計算好的復合損傷變量代入式(26)中，可得到紅砂巖理論應力-應變曲線。通過對比實測曲線可對本構模型的準確性進行驗證(見圖9)。

圖9 含水紅砂巖動態本構模型檢驗

從圖9可看出，利用本構模型所推導出的理論應力-應變曲線與實測應力應變曲線在試樣臨界破壞前，即峰前階段擬合度較高；試樣破壞后，理論與實驗的結果差異較大。這是由于復合損傷變量未達到1，即紅砂巖未達到臨界破壞時，紅砂巖的強度主要由外部荷載對巖石施加的力使得紅砂巖產生軸向應變導致；在試樣破壞后的階段，紅砂巖的殘余應力主要是由破碎的巖塊提供，由于巖石破壞的不均勻與不確定性，導致峰后階段應力下降時理論與實測曲線擬合度一般。從上圖可知，該本構模型并不能與含水紅砂巖在動態壓縮下應力-應變曲線的各個階段完全對應，還需要進一步的改善。

5 結論

1)推導得到了紅砂巖在含水率與應變率耦合作用下的復合損傷變量與動態損傷本構方程。

2)含水損傷D1在一定范圍內隨含水率的增加而逐漸擴大，隨著試樣逐漸飽和，含水損傷趨于穩定。復合損傷Dω與荷載損傷D2在應變率的作用下變化趨勢近似，分為3個階段，即初始階段、低速發展階段與快速發展階段。3個階段代表了巖石受動荷載作用時的破壞過程，可與含水紅砂巖動態壓縮破壞過程應力-應變曲線的各個階段相對應。

3)推導建立的含水紅砂巖動態損傷本構模型，可以較好地描述含水紅砂巖動態壓縮應力-應變曲線的各個階段，驗證了該模型的準確性與合理性。