一類高階非線性分數階多點邊值問題解的存在性
劉 暢,王文霞
(太原師范學院 數學系,山西 晉中 030619)
0 引言
分數階微積分的概念是整數階微積分到任意階的推廣。相比于整數階導數,分數階導數可以更好地描述過程的記憶性和遺傳性。分數階微分方程在自動控制、航天技術、信號識別、生物數學、物理學、力學等領域廣泛應用。
分數階微分方程邊值問題近年來備受關注,見文獻[1~4]。在不同邊界條件下的微分方程解的存在性是分數階微分方程理論研究的一個重要領域,見文獻[5~8]。近年來一些作者研究了高階分數階微分方程的邊值問題,見文獻[9~11]。
文獻[9]研究了如下分數階微分方程m點邊值問題正解的存在性:
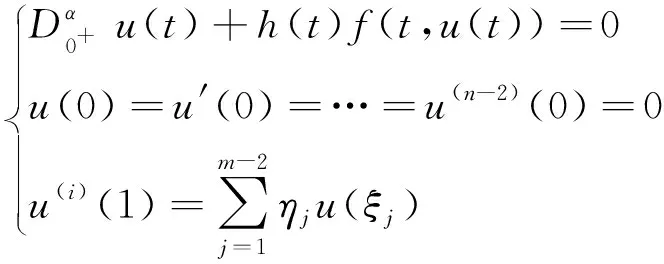
(1)
其中i≥0是整數,n為整數,i≤n-2,α≥2,0 文獻[10]研究了如下非線性項依賴未知函數的分數階導數,且具有非線性邊界條件的分數階微分方程的邊值問題: (2) 其中n>3,1≤γ≤β≤n-2,f∶[0,1]×[0,∞)×[0,∞)→[0,∞),g∶[0,1]×[0,∞)→[0,∞),k∶[0,∞)→[0,∞)是連續函數。作者運用了錐上的不動點理論,得到了邊值問題(2)的唯一正解存在的充分條件。 文獻[11]研究了如下分數階微分方程無窮點邊值問題: (3) 其中α>2,n-1<α≤n,i∈[1,n-2]是整數,αj≥0,0<ξ1<ξ2<…<ξj-1<ξj<…<1 (j=1,2,…)。作者運用Schauder不動點定理,建立了邊值問題(3)正解的存在性定理。進一步,利用凹算子的不動點定理給出了邊值問題正解的存在唯一性結果。 受上述文獻啟發,本文研究如下高階非線性分數階微分方程多點邊值問題: (4) 其中n>3,1<γ≤β≤n-2,j∈[1,n-2]是整數,0≤ξ≤1,0<η≤1,a,b,λ,μ都為正數,f∶[0,1]××→,g∶→是連續函數,是Riemann-Liouville導數。 本文運用Leray-Schauder非線性抉擇原理,討論邊值問題(4)解的存在性的充分條件。 定義1[1]連續函數f∶(0,+∞)→的α>0階Riemann-Liouville分數積分定義為 其中,等式的右端在(0,+∞)有定義。 定義2[1]連續函數f∶(0,+∞)→的α>0階Riemann-Liouville分數導數定義為 其中n=min{m∈∶m≥α},等式的右端在(0,+∞)有定義。 引理1[1]假設u∈C(0,1)∩L(0,1)有α>0階導數屬于C(0,1)∩L(0,1).則 ci∈,i=1,2,…,n,其中n大于或等于α的最小整數。 引理2 若h(t)∈C[0,1],則下面邊值問題 有唯一解x(t)且 其中 證明 由引理1,將微分方程轉化為等價的積分方程 于是 由xi(0)=0得,cn=cn-1=cn-2=…=c2=0.即 則 于是 故 因此我們得到 證畢。 引理3 函數G(t,s)滿足以下性質: 1)G(t,s)在[0,1]×[0,1]上是連續的; 2) ?(t,s)∈[0,1]×[0,1],有 證明 由G(t,s)在表達式可知結論1)成立。以下證明結論2)成立。 ?(t,s)∈[0,1]有 證畢。 類似于引理3的證明可得 我們引入如下記號 下是一個Banach空間。 定義算子T∶E→E如下 則 引理4[4](Leray-Schauder非線性抉擇原理)設F是Banach空間,Ω?F是凸的,且0∈Ω.若T∶Ω→Ω是一個全連續算子,則下列結論至少有一個成立: i)算子T在Ω上有一個不動點, ii)集合E={x∈Ω∶x=λT(x),0<λ<1}是無界的。 本文將用到如下假設: H1)存在非負函數ω(t),φ(t)∈L1[0,1],使得 |f(t,u,ν)|≤ω(t)|u|+φ(t)|ν|,?t∈[0,1],u∈+,ν∈+ 且 注2 若條件H2)滿足,則存在k>0,使得 |g(x)|≤k 定理1 假設H1),H2)成立,則算子T∶E→E全連續。 證明 首先證明T∶E→E是連續的。 由條件H1)可知 <2l[ω(s)+φ(s)] 由Lebesgue控制收斂定理可知, 于是由條件H1)、H2)和注1可得, 故有 設Ω為E中的有界集,則存在常數r>0,使得 以下證明T(Ω)是相對緊的.對任意的x∈Ω有 此外,因為G(t,s),G1(t,s)在(t,s)∈[0,1]×[0,1]上一致連續,所以?ε>0,?δ>0,使得當t1,t2∈[0,1],|t1-t2|<δ時有 進而對?x∈Ω有 <ε <ε 即TΩ等度連續。 由Arzela-Ascoli定理可知,算子T∶E→E是全連續算子。證畢。 定理2 假設條件H1)、H2)滿足,則邊值問題(4)在E上至少有一個解。 證明 設X={x∈E|x=λTx,λ∈(0,1)},由引理4可知只需證明集合x是有界的。當x∈X時x=λTx,對?t∈(0,1)有 |x(t)|=|λTx(t)|≤|Tx(t)| 因此 故集合X有界。由引理4可知算子T至少有一個不動點,則邊值問題(4)至少有一個解。 例 考慮下面邊值問題 顯然有 通過簡單計算可知,Γ(α)≈11.632,Γ(α-β)=1,Γ(α-γ)=2,進而有 故 于是定理2條件都滿足,所以邊值問題(4)至少存在一個解。 Existence of solutions for a class of higher order nonlinear fractional multipoint boundary value problems LIU Chang,WANG Wen-xia


1 預備知識和引理

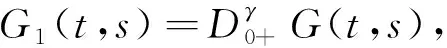

2 主要結果











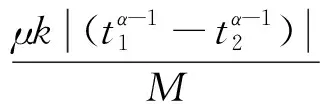
3 示例


