基于優化BP神經網絡算法的隧道巖土體力學參數分析方法研究

龔 盛，楊 柱，張國鵬，羅 曦，陳興周

(1. 西安科技大學 建筑與土木工程學院,西安 710054；2. 中國電建集團西北勘測設計研究院有限公司,西安 710065)

0 前 言

隧道開挖破壞了地層的天然應力狀態，受賦存現場的地下水、隧道上覆荷載、施工方式等復雜工程條件的影響，引起應力重分布并隨時程而變化[1]。而由于土體結構的復雜性以及土體材料的非均質、非線性、不連續的特性，使得土力學參數的確定一直是工程界的難題之一，為此，獲取符合實際的圍巖參數進行支護設計尤為重要[2-3]。土體力學參數可以通過室內試驗和原位試驗獲得，然而，這些試驗獲得的參數都是試樣的力學參數，實際工程中土層的性狀復雜，試樣的力學參數無法很好的反映土層的強度、變形特征[4]。基于現場監測的位移反分析方法是確定土體力學參數的有效方法之一，并且其在隧道的穩定性評價、施工設計以及變形預測中發揮著重要作用。

范新宇[5]等針對水庫邊坡變形受水位線升降影響的特點，采用神經網絡預測了庫水位變化和降雨對邊坡變形的影響；張爭[6]等利用Phase2聯合 MATLAB神經網絡工具箱進行圍巖參數反演，進行隧洞圍巖變形分析，計算結果與監測數據變化規律一致；柏俊磊[7]采用BP神經網絡對水電站高邊坡進行參數反演，通過有限元計算驗證所得參數能較好地反應巖體開挖后的位移變化規律。Zheng Zhaoliang[8]等采用人工神經網絡模型(ANN)和粒子群優化模型算法對邊坡進行位移反分析，根據不同開挖階段的監測位移數據獲得巖體的彈性模量；Yong Zhao和Shi-Jin Feng[9]在考慮了位移損失和空間效應的基礎上，使用粒子群優化算法優化極限學習機，提出了一種基于巖石位移參數反演的方法；原先凡[10]等基于有限差分軟件建立模型，并利用BP神經網絡模型對考慮開挖卸荷狀態下的隧道圍巖力學參數進行反分析；張志華[11]等基于神經網絡計算分析了土體變形量與其對應的力學參數之間的非線性關系。

本文將CO-RDPSO算法優化神經網絡運用到隧道工程反分析當中，根據監測位移反演土體力學參數，并且用文獻算例進行了驗證并反演參數，可為后續支護設計安排提供參考。

1 基于 CO-RDPSO 神經網絡的參數反演方法

在隧道穩定性分析中，土體力學參數選取的合理性決定著計算的正確性，因此有必要進行土體力學參數反演，獲得與工程較為符合的土體力學參數尤為重要。土體力學參數的辨識一般有正分析和反分析兩種。正分析即是通過室內試驗、原位試驗或力學計算等方法進行正向確定參數；反分析則是通過現場監測位移等結果數據來逆向確定參數的方法。受地質體構造復雜性等的影響，通過正向分析得到的參數與工程實際相差較大。本文采用位移反分析的方法并基于BP神經網絡算法來獲取隧道土體力學參數。

1.1 BP神經網絡

BP神經網絡是一種前向傳播的神經網絡，由輸入層、隱含層、輸出層構成輸入數據與輸出數據間的非線性映射，它的信息是正向傳遞的，誤差則是反向傳播的，其基本思想是將預測值與期望間的誤差由輸出層反向傳播，用以調整各個連接神經元之間的權值和閾值，通過多次迭代誤差找到合適權值和閾值，使誤差逐漸減小，網絡實際輸出值不斷逼近期望輸出，神經網絡信息傳遞方式如圖1所示。常規的BP神經網絡采用梯度下降法對誤差進行傳播, 但由于初始權值和閾值是隨機設定的，使得BP神經網絡常出現、易陷入局部最優、網絡學習率不穩定、收斂速度慢等缺陷。

圖1 BP神經網絡結構

1.2 交叉算子的隨機漂移粒子群算法CO-RDPSO

粒子群優化算法(Particle Swarm optimization,PSO)是Poli R和Kennedy J[12]提出的進化算法的一個重要分支，是一種通過全局粒子最優位置和粒子個體最優位置調整下次迭代位置的尋優計算方法。在尋找函數最小值方面具有很強的優化性能，并且收斂速度快。

(1)

(2)

公式(1)～(2)中：W是慣性權重；c1和c2是學習因子，用于調整算法的收斂速度；r1，r2為在[0，1]范圍內正態分布的隨機數。

(3)

公式(3)表明整個種群的收斂會使每個粒子在各自的Pi,n和Gn組成的超矩形附近進行搜索，反映了標準PSO 算法中粒子偏局部的搜索行為，使得標準 PSO 算法在迭代后期易于陷入局部收斂。

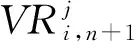
(4)

(5)

(6)

(7)

綜上，RDPSO算法的速度更新公式可寫為：

(8)

Holland 受自然界生物進化提出了遺傳算法，該算法自20世紀70年代提出以來在解決優化問題上得到了廣泛的使用[15]，其中交叉算子是遺傳算法優化的主要工具，將交叉算子運用到粒子群算法上也有著優秀的表現。交叉學習可以利用已有的優秀粒子構造新的粒子，不僅可以提高粒子的種群多樣性，避免粒子過早收斂，同時使得粒子的搜索范圍更大，更有機會跳出局部收斂。

(9)

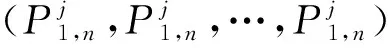
(10)

R=(t/nmaxiter)×M

(11)

公式(11)中:t為迭代次數；nmaxiter為最大迭代次數；M為粒子總數。

(12)

(13)

最后應用隨機漂移粒子群算法進行速度和位置的更新，如公式(8)和公式(2)所示。

1.3 CO-RDPSO優化神經網絡反演流程

基于CO-RDPSO 算法的隧道力學參數反演分析流程如下：首先依據地質及施工資料建立隧道數值仿真模型，在反演參數取值范圍內進行均勻采樣，帶入數值模型計算生成訓練樣本。采用CO-RDPSO 算法對 BP神經網絡的初始權值和閾值進行優化，使神經網絡能夠更好地反映隧道變形與圍巖力學參數之間的非線性映射關系。將實測位移帶入訓練好的神經網絡，通過不斷迭代優化尋找最貼近實際監測數據的材料參數，最后利用數值模型和計算反演參數下隧道的位移，通過計算位移與實測位移的對比評價反演效果。

2 工程算例

2.1 數值模型

采用文獻[16]中的案例驗證CO-RDPSO算法優化BP神經網絡的效果。某地鐵隧道采用盾構施工，隧道外徑 6.0 m，襯砌厚 0.3 m，建模時采用實體單元模擬襯砌，土體密度1 800 kg/m3，其他參數詳見表 1。地表覆蓋 3～5 m厚雜填土，主要由黏性土、石灰巖碎石、建筑垃圾以及生活垃圾等組成，下層主要是中風化白云質灰巖，巖體節理裂隙較發育。

表1 土體參數參考值

依據文獻資料建立的數值模型如圖2所示，模型的尺寸為50 m×40 m×30 m(長×寬×高)，模型的四周和底面設置法向約束，模型頂面采用自由邊界，由于隧道中心點到模型頂面的距離小于隧道中心點到實際地面的距離，在模型頂面施加1.4 MPa的法向力，用于模擬土層和地面荷載。隧道采用全斷面開挖法施工，開挖進尺為2 m，在隧道拱頂和拱腰處設置兩個監測點，監測該處的位移值作為數據集輸入樣本，將數據集分為訓練集和測試集對神經網絡進行訓練，并測試神經網絡的預測效果。

圖2 數值計算模型

模型采用的力學參數如表1所示。結合表1中參數的變化區間，丁德馨[17]等采用數理統計分析方法確定了彈塑性位移反分析的可反演參數，其中對變形影響最大的參數主要是彈性模量和泊松比，因此本文主要對彈模和泊松比進行反演，將彈性模量、泊松比均勻分為5個水平，進行正交實驗，得到了25個訓練樣本集，將數值模擬得到的位移值作為數據集輸入值，土體力學參數作為輸出值，得到初始數據集對神經網絡進行訓練與驗證，學習樣本如表2所示。

表2 神經網絡學習樣本

2.2 構建樣本集訓練神經網絡

利用CO-RDPSO算法優化 BP 神經網絡權值和閾值，研究表明隱含層數量對BP神經網絡的準確性影響不大[18]，并且過多的隱含層可能會導致神經網絡出現過擬合的現象，因此本文只選取了一層隱含層，隱含層神經元個數為12個，以均方誤差MSE作為目標函數，利用粒子群算法進行多次尋優計算，單次計算時最大迭代次數為200次，以多次訓練中目標函數最小處粒子的位置作為神經網絡的初始權值和閾值，即完成了神經網絡的訓練。

將隧道開挖2 m處斷面的實測值代入訓練好的神經網絡，其訓練迭代過程誤差曲線如圖3所示，圖3中的適應度即為誤差均方MSE，隨著迭代的進行誤差逐漸減小，當誤差趨于最小時建立最終的BP神經網絡。利用神經網絡計算得到土體楊氏模量為0.358 2 GPa、泊松比μ為0.271 4，因為選取的神經網絡訓練樣本不一樣，本文所得土體力學參數與文獻計算結果有一定誤差，但兩文中參數值非常接近。

圖3 BP神經網絡訓練誤差曲線

2.3 結果分析

將E、μ帶入數值模型獲取模擬位移值，其位移對比如圖4所示，拱頂與拱腰反演參數模擬位移與監測位移誤差分別為0.2% 和 0.75%，分析誤差產生的原因主要有：① 粒子群粒子個數設置為100個，相較于神經網絡權值閾值個數較少；② 本文采用的為單目標粒子群優化算法，目標函數僅有一個，可將平均絕對誤差、均方根誤差作為目標函數，得到不同目標函數下的神經網絡。

圖4 監測點計算位移與預測值對比

3 結 論

(1) 基于神經網絡,對利用正交設計試驗并結合數值模型的樣本集進行訓練,得到了訓練收斂的神經網絡,可以方便地反演計算圍巖力學參數。

(2) 采用CO-RDPSO算法，不僅能提高其全局搜索能力，還能夠加快神經網絡的收斂速度，改善神經網絡易于陷入局部最優解的問題，又利用了神經網絡非線性映射特點，從而能夠得到反演參數的最優解。