運動學約束下直線轉角非對稱平滑加工規劃
何昱龍 琚長江 楊根科 王成光
1.上海交通大學寧波人工智能研究院,寧波,315000 2.上海交通大學自動化系,上海,200240 3.寧波工業互聯網研究院,寧波,315000
0 引言
高速高精度加工一直是現代計算機數控系統亟待解決的問題,平滑的刀具路徑和進給速率是實現所需加工質量的關鍵。在計算機輔助設計系統中,可以使用非均勻有理B樣條曲線等光滑樣條插補曲線來描述刀具軌跡[1],計算機輔助制造系統常直接采用直線段(G01)擬合逼近曲線的方式輸出刀具軌跡[2-4],零件的幾何外形也可能包含帶有轉角的長直線段刀具軌跡。直線段刀具軌跡在轉角處僅考慮了位置連續,忽略了速度與加速度的連續變化,在零件加工時,刀具在轉角處必須完全停止以避免驅動器因超過機械極限而引起慣性振動、破壞零件表面光潔度,導致加工效率低。
為平滑G01刀具軌跡,實現不間斷的連續運動,目前主要有兩種方法:全局平滑[5-6]與局部轉角平滑[2-4,7-12]。全局平滑將所有線性軌跡進行擬合,生成連續參數刀具軌跡,計算量大[3]且難以評估平滑過程中產生的誤差;局部轉角平滑使用指定的參數曲線在定義的公差范圍內混合相鄰的線段,計算量小,有利于誤差評估與實時計算。
一般局部轉角平滑研究[2-4]會分離幾何誤差約束與運動學約束,使平滑過程主要分成兩步:先插入參數曲線,然后規劃運動軌跡。這種方法僅考慮切向運動限制,造成執行器大量性能損失,并且參數曲線的弧長難以解析,用弦長代替弧長會引入額外誤差造成速率波動。為解決此問題,近年來出現一種不需要參數曲線擬合的轉角軌跡平滑方法,該方法在刀具軌跡平滑規劃的同時進行運動軌跡規劃。TAJIMA等[8]提出了兩種基于運動學的轉角平滑規劃方法,并在文獻[6]中加以優化,生成了加加速度限制下的加速度不間斷轉角平滑軌跡。一般情況下,G01轉角開始和結束所在直線運動學約束并不相同,TAJIMA等[6]提出的轉角平滑方法基于直線轉角運動開始與結束時進給速率與加速度大小相同的對稱假設,無法充分利用執行器性能。為此,ZHANG等[9]提出了一種直接生成非對稱時間最優的轉角平滑軌跡方法,但忽略了加速度的突變。WANG等[11]提出了基于整體加工時間優化的非對稱轉角平滑規劃方法,相比文獻[8]可以取得更好的效果,但在求解過程中需要多次迭代,不適用于實時計算轉角平滑軌跡生成。ZHANG等[10]提出了一種直線段進給速率混合的方法,實現了非對稱的轉角平滑規劃,但轉角處加加速度的約束過強制約了執行器性能的發揮。
本文對可以達到給定進給速率的平面G01刀具軌跡進行了研究。在S型速度軌跡規劃的前提下,通過對轉角處運動學和幾何誤差約束的分析,提出一種直線轉角的非對稱平滑規劃方法,實現進給速率與刀具軌跡的同時規劃,利用軸向加加速度與誤差約束解算準時間最優的刀具軌跡轉角平滑參數。
1 單軸初末速度、加速度不為零的S型速度軌跡規劃
S型速度軌跡規劃又稱加加速度限制速度軌跡規劃,引入了加加速度限制使加速度連續,從而使速度軌跡具有柔性,有效抑制運動中的殘余振動[12-13]。完整的S型速度規劃分為以下7個階段:加速度增加階段(Ⅰ階段)、加速度恒定階段(Ⅱ階段)、加速度減小階段(Ⅲ階段),速度(速率)恒定階段(Ⅳ階段)、減速度增加階段(Ⅴ階段)、減速度恒定階段(Ⅵ階段),減速度減小階段(Ⅶ階段),如圖1所示。其中,階段Ⅰ、Ⅱ和Ⅲ統稱加速階段,階段Ⅴ、Ⅵ、Ⅶ統稱減速階段。

圖1 七段式S型速度軌跡
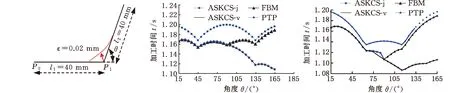
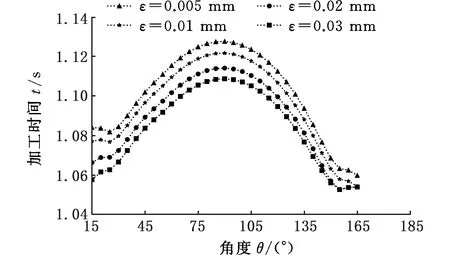
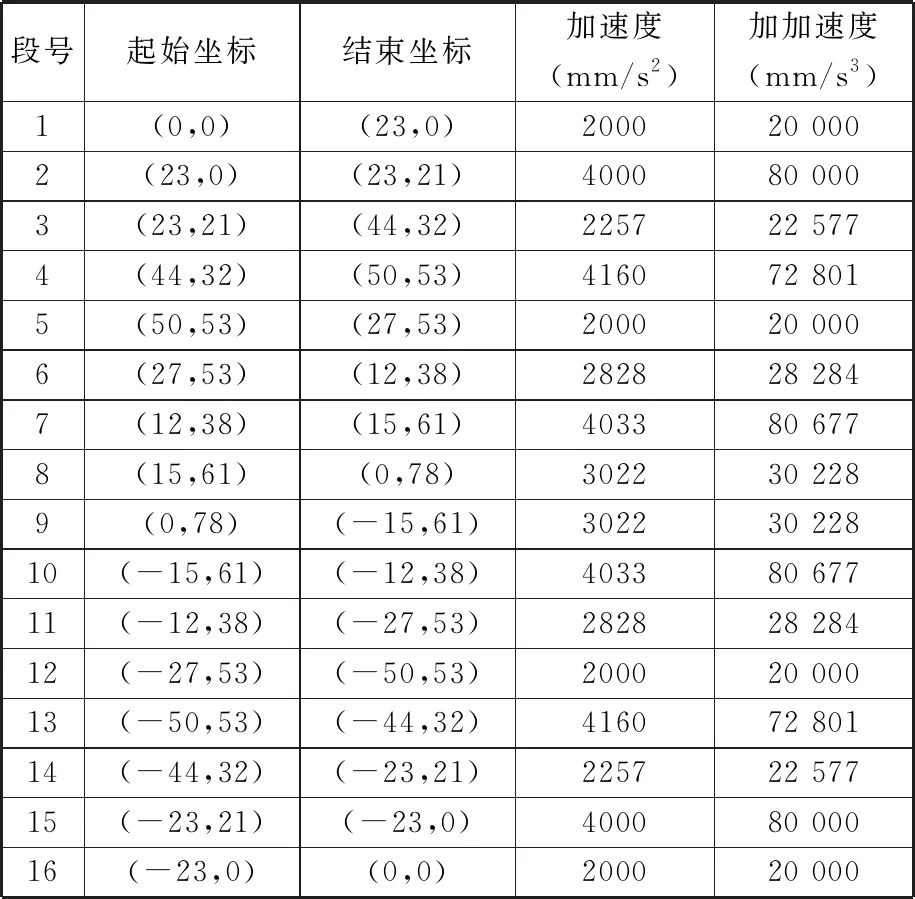
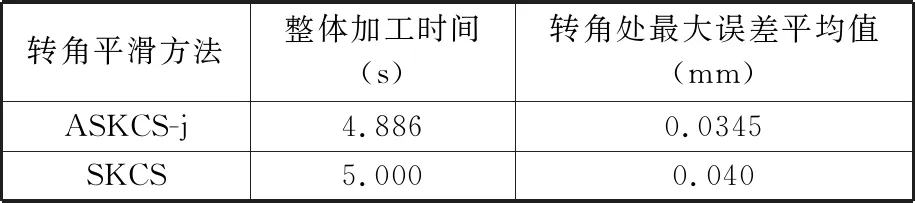
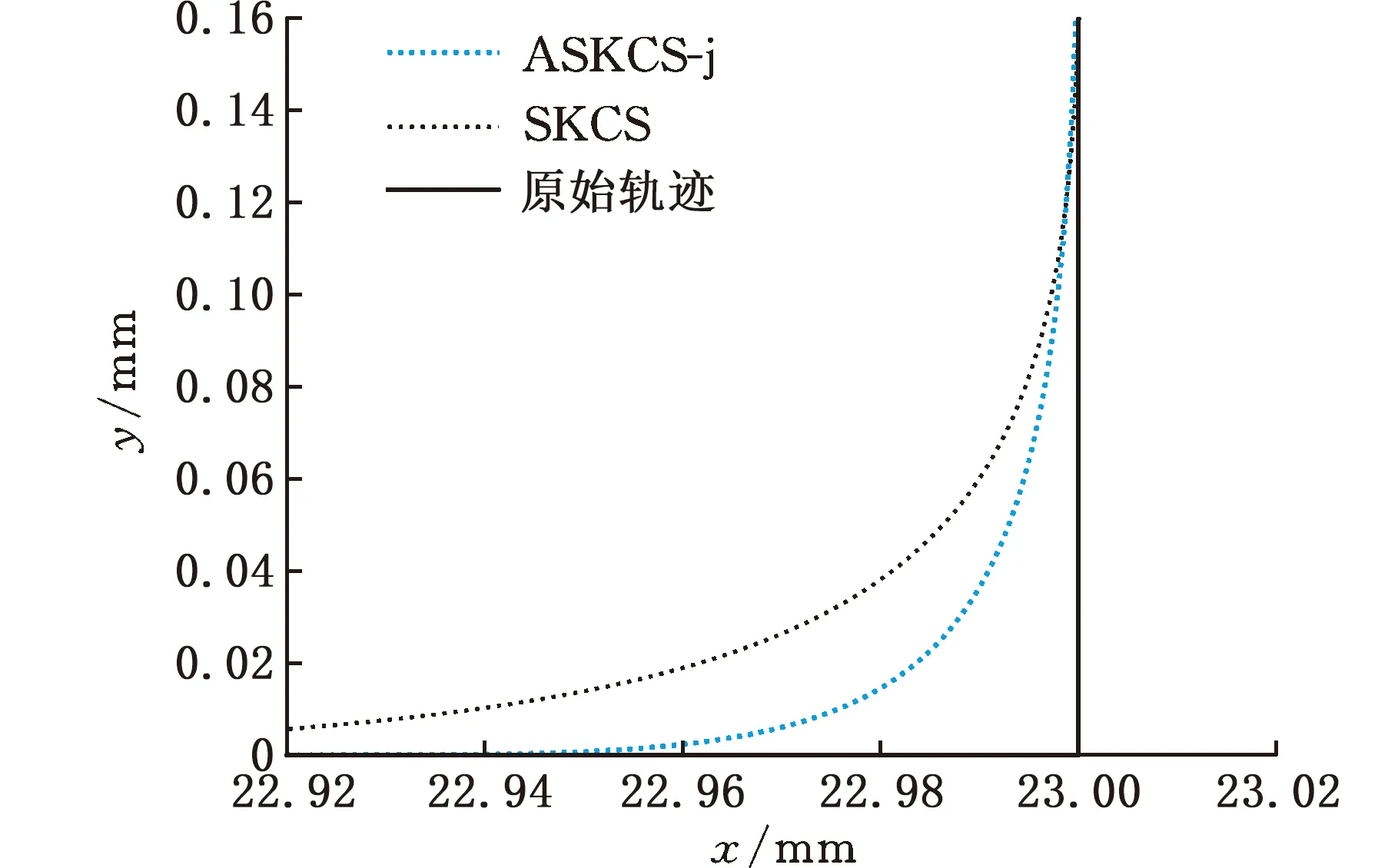
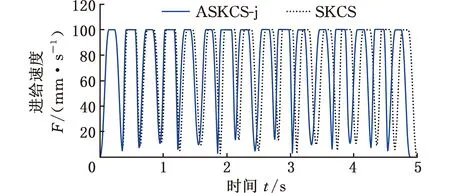
在初末速度、加速度不為零的運動中,系統給定最大速度為vmax,最大加速度為amax,最大加加速度為jmax,則運動過程可描述為從給定開始速度vs(0 主要分析加速段(Ⅰ、Ⅱ、Ⅲ)的運動輪廓,從vs(vs 圖2 四種加速段情況 首先給出階段Ⅰ、Ⅱ、Ⅲ均存在的加速段加加速度、加速度和速度的運動軌跡方程: (1) (2) (3) v2=v1+amaxT2a 式中,J(t)、A(t)、V(t)分別為t時刻的加加速度、加速度、速度;i=Ⅰ,Ⅱ,Ⅲ表示不同的運動階段;τi=t-ti,ti為第i階段的結束時間;Tia為第i階段的持續時間;vi為第i階段結束時的速度。 下面介紹各時間段的求解方法。加速段速度差值Δv=vmax-vs,定義Δvf為as以最大加加速度直接減為0時速度的改變量,即滿足 (4) 當Δv=Δvf時,僅階段Ⅲ存在,則有 T1a=T2a=0T3a=as/jmax (5) 當Δv<Δvf時,加速度先減小后增大,加速段不存在此情況;當Δv>Δvf時,T2a存在的條件為 若as (6) 當as=amax時,階段Ⅱ、Ⅲ存在,T1a=0,T2a、T3a的計算公式同式(6)。 (7) T1a、T3a分別為 (8) 減速段同理,不再贅述。作為特例,初末速度加速度為零的S型速度軌跡規劃,可令vs=ve=as=ae=0獲得。 經過不同直線段的相交處時,允許轉彎速度不完全減為零,以減少電機的頻繁啟停,提高運動效率。 如圖3所示,兩直線交點為Pc,es和ee分別表示兩條直線上運動方向的單位向量,θs和θe分別為兩向量與x軸正向夾角;ε為給定的轉角點Pc到轉角平滑曲線的最大容許誤差;Ps和Pe分別為轉角平滑運動的開始點與結束點,Vs、As分別為開始點處的速度與加速度,大小為Vs、As,PsPc為開始點到轉角點的位移,長度為ls;Ve、Ae分別為結束點處的速度與加速度,大小為Ve、Ae;PcPe為轉角點到結束點的位移, 長度為le;J為轉角平滑時的加加速度,J=Js+Je=jses+jeee,Js、Je分別為J在es和ee方向上的投影,大小為js、je。在單次直線轉角平滑過程中,js與je保持不變。可寫為 圖3 直線轉角的非對稱平滑規劃軌跡示意圖 (9) 在轉角平滑運動過程中,其矢量運動學方程可寫為 (10) 其中,τ∈[0,Tc];Tc為直線轉角平滑過程的持續時間;Aτ、Vτ、Sτ分別為τ時刻的加速度、速度與位移;Vτs、Vτe分別為τ時刻Vτ在es和ee上的分量。τ時刻的矢量合成圖見圖4。 圖4 直線轉角非對稱平滑規劃中運動學矢量合成示意圖 當τ=Tc時,轉角平滑運動結束。將τ=Tc代入式(10),并將以上運動學矢量分別向es和ee方向投影,聯立式(9)可獲得轉角平滑運動的邊界處參數ls、le、As、Ae、Vs、Ve與js、je、Tc的關系: (11) 在轉角平滑的運動過程中,任意τ時刻到Pc距離的平方為 (12) 設τε時刻為轉角運動平滑過程中距離Pc最近的時刻,則有 ‖PcPτ‖2≥‖PcPτε‖2 (13) 提高最大容許誤差有利于提高加工效率[8,11],故令‖PcPτε‖2=ε。由于τε的計算過程復雜,故基于式(12)和式(13)的特殊形式,選擇τ=Tc/2處的軌跡點與Pc的距離為最大容許誤差的邊界值,即‖PcPTc/2‖2=ε,這保證了轉角平滑軌跡在規定的誤差范圍內,即 ‖PcPτε‖2≤‖PcPTc/2‖2=ε (14) 基于式(12)與式(14),可用js、je對Tc進行解析表示,即 (15) 聯立式(14)與式(17),可通過js、je兩個決策參數對直線轉角平滑的運動軌跡進行描述。 一般情況下,在平面的直線運動中,由于需要對x、y軸的速度進行耦合,為實現準時間最優,僅能達到單軸運動學極限,此時有 (16) 式中,Ams、Ame分別為轉角開始與結束所在直線段的直線運動中的加速度邊界;Jms、Jme為加加速度邊界;Amx、Amy分別為x軸與y軸的軸向加速度極限;Jmx、Jmy為軸向加加速度極限。 在轉彎過程中,可能同時達到x、y軸的加加速度極限,即 (17) 由于Vs與Js同向,Ve與Je同向,且在加工過程中,速度方向恒為正向,則有 js>0je>0 (18) 為確定轉角平滑時的運動軌跡,需要確定js、je,即針對式(17)的求解。隨著θs與θe的變化,在式(18)的約束下,式(17)的解出現無解、單解、雙解三種情況,在無解情況下需要進行修正,此時僅能滿足單軸加加速度極限。三種情況對應的軸向加加速度分解如圖5所示。 (a)無解 (b)無解修正 為求解js、je,并充分利用x軸與y軸的軸向加加速度極限,本文采用以下兩種優化模型。 (1)模型1。基于速度的非對稱運動學直線轉角平滑(velocity-based asymmetrical kinematics corner smooth,ASKCS-v),即最大化直線轉角開始與結束時的進給速率和: max(Vs+Ve) (20) 注意到此約束中存在等式,且Vs、Ve和Tc均可由js和je表示,可將模型簡化為 (21) (2)模型2。基于加加速度的非對稱直線轉角平滑(jerk-based asymmetrical kinematics corner smooth,ASKCS-j),即最大化直線轉角開始段與結束段的加加速度較小值: (22) 在轉角處,不需要多軸的耦合,為了實現加速度的連續變化,仍需要對加速度進行單軸極限的限制,即 (23) 其中,A′ms、A′me分別為開始與結束所在直線段的直線運動中可達到的最大加速度,F為最大進給速率。若超過約束,則重新修正轉角時間: (24) 在轉角平滑的過程中,由于最大容許誤差的存在,轉彎處的允許進給速率較小,一般無法達到給定的進給速度,如果轉角鈍化嚴重,即|θe-θs|趨近于180°,出現Vs>F,在這種情況下,令Vs=Ve=F,As=Ae=0,根據文獻[8]所述方式在轉角處進行平滑規劃。 ASKCS-v(模型1)包含高次項,采用序列最小二乘規劃算法進行迭代求解。 ASKCS-j(模型2)為簡單的線性規劃問題,最優解存在于邊界,求解步驟如下: (1)求解式(17)可得4個坐標點(jsi,jei),i=1,2,3,4。 (3)令mini=min(jsi,jei),i=0,1,…,4,記k為{mini}中最大值的下標,(jsk,jek)即目標解,結束。 兩種優化模型均旨在獲得轉角處的最大進給速率以滿足速度規劃中的準時間最優。ASKCS-v優化模型納入對Tc的考慮,進一步約束了轉角平滑過程;ASKCS-j為簡單的線性規劃問題,求解簡單,有利于進行轉角平滑軌跡的實時規劃。 首先在單轉角刀具軌跡中對比ASKCS-v與ASKCS-j在各種轉彎角度下的性能表現,然后在連續轉角刀具軌跡中將ASKCS-j與文獻[6]中的對稱轉角平滑(symmetrical kinematics corner smooth,SKCS)算法進行對比。 兩條直線段P0P1和P1P2構成的單轉角刀具軌跡如圖6a所示,兩條直線段長度均為40 mm,最大進給速率Fm=100 mm/s,規定運動狀態為從P0處完全靜止(速度與加速度均為0)開始到P2處完全靜止結束,P1P2與x軸正向的夾角從15°到170°變化。對比了ASKCS-v與ASKCS-j在最大容許誤差ε=0.02 mm的情況下,給定不同軸向加速度與軸向加加速度極限(具體數值在圖6a中已給出)的加工時間,并將文獻[10]的進給速率混合(feedrate blengding method, FBM)和運動在轉角處完全靜止(point to point, PTP)的運動規劃方法納入對比,仿真結果如圖6b~圖6f所示。對比了ASKCS-j在Amx=1 m/s2,Amy=2 m/s2,Jmx=20 m/s3,Jmy=10 m/s3的條件下,不同最大容許誤差(具體數值圖中已給出)約束下的加工時間,結果如圖7所示。 (a)單轉角刀具軌跡 (b)Amx=1 m/s2 ,Amy=1 m/s2Jmx=10 m/s3,Jmy=10 m/s3 (c)Amx=1 m/s2,Amy=2 m/s2Jmx=10 m/s3,Jmy=20 m/s3 圖7 不同誤差約束下ASKCS-j單轉角加工時間對比 由圖6b~圖6f可看出,相比PTP的規劃方法,FBM、ASKCS-v與ASKCS-j在加工時間上均有減少,當兩直線夾角為銳角時,ASKCS-v與ASKCS-j可以節省更多的加工時間;在加工時間方面,ASKCS-v在銳角情況下略優于ASKCS-j,但在求解速度方面,ASKCS-j明顯快于ASKCS-v,在工程上可進行實時的轉角平滑規劃。由圖7可看出,當最大允許誤差增大時,加工時間縮短,這是由于提高最大允許誤差可以實現更大的進給速率通過轉角。最大允許誤差的存在,柔滑了直線夾角,實現了加工過程中速率、加速度的連續性。 將ASKCS-j與SKCS用于圖8所示的“楓葉”刀具軌跡的轉角平滑中,并對結果進行了比較分析。“楓葉”刀具軌跡設有不同角度的轉彎,且路徑存在對稱性,有利于考察轉角平滑算法的綜合性能。 圖8 “楓葉”刀具軌跡 “楓葉”軌跡中的運動學約束與最大允許誤差見表1;“楓葉”軌跡的坐標與在直線運動中的運動學邊界見表2;兩種平滑規劃方法在各轉角處的運動參數見表3;加工完給定的“楓葉”刀具軌跡的整體加工時間和在各轉角處最大誤差的平均值見表4;部分轉角處的平滑軌跡如圖9所示。“楓葉”刀具軌跡中的運動學軌跡曲線(局部)如圖10所示。 表1 “楓葉”刀具軌跡中的約束 表2 直線段坐標及直線運動中的運動學邊界 表3 轉角處的運動參數 表4 加工時間與轉角誤差平均值 (a)轉角(1) (a)進給速率 上述仿真結果表明,基于兩種模型的規劃方法均將軸向加加速度約束在給定范圍內,實現了進給速率與軸向加速度的連續變化;相比SKCS,本文提出的ASKCS-j在轉角處更能充分利用執行器的性能,縮短運動時間,獲得更平滑的軌跡,將刀具軌跡的整體加工時間縮短了2.3%,最大誤差平均值減小了13%。可見,ASKCS-j可以在運動學與幾何誤差約束下提供更準確的軌跡,并能提供更短的加工時間,滿足高速高精度加工需求。 為驗證ASKCS-j方法的有效性,搭建了圖11所示的運動控制實驗平臺,該平臺主要采用倍福twincat3運動控制軟件、三菱PLC和松下伺服驅動器和伺服電機(型號MINAS-A6B)。 圖11 實驗平臺實物圖 設定系統參數,進給速度最大為100 mm/s,允許最大誤差為0.04 mm,x軸與y軸的加速度與加加速度分別為Amx=2 m/s2,Amy=2 m/s2,Jmx=50 m/s3,Jmy=50 m/s3。加工實驗軌跡參考圖見圖12a,實際加工情況如圖12b所示;仿真進給速率變化如圖12c所示,實際加工過程中的進給速度圖見圖12d。 (a)實驗參考軌跡 (b)實際加工情況 如圖12c、圖12d所示,ASKCS-j仿真過程的整體運動時間為7.52 s,實際運動的時間為7.74 s,仿真結果與實際結果在運動速度、運動時間存在差距,這是由于實際的運動系統為離散系統,針對連續系統進行采樣的周期固定,造成部分數據點丟失;同時在運動過程中存在實際慣量、摩擦等多方面物理因素,造成運動過程的抖動,但仿真結果與實際結果差距在一定的范圍內,可以認為實際結果與仿真結果相同。因此,本文方法保證了加工過程中進給速率的連續變化,并實現了轉角過程中進給速率不完全減為0,減少電機的頻繁啟停,提高了加工效率。 本文針對直線段刀具軌跡的非對稱轉角平滑規劃進行研究,通過運動學分析提出了一類兩種指標下可解析的加加速度有限的直線轉角非對稱平滑規劃方法,通過仿真實驗與樣機實驗驗證了該類方法的可行性與有效性。該規劃方法可以同時實現進給速率與刀具軌跡的平滑規劃,獲得連續變化的進給速率和軸向加速度變化曲線;充分利用驅動器的性能,無需迭代直接解析轉角平滑時的軌跡參數,得到更好的、非對稱的轉彎平滑軌跡,相比對稱轉角平滑規劃,本文方法具有更小的誤差和更短的加工時間的優點,能夠滿足高速高精度加工的需求。本文方法以兩軸平面直線加工為研究基礎,可推廣到笛卡兒坐標系下任一平面的直線加工,三軸及三軸以上的加工也可考慮采用本文方法。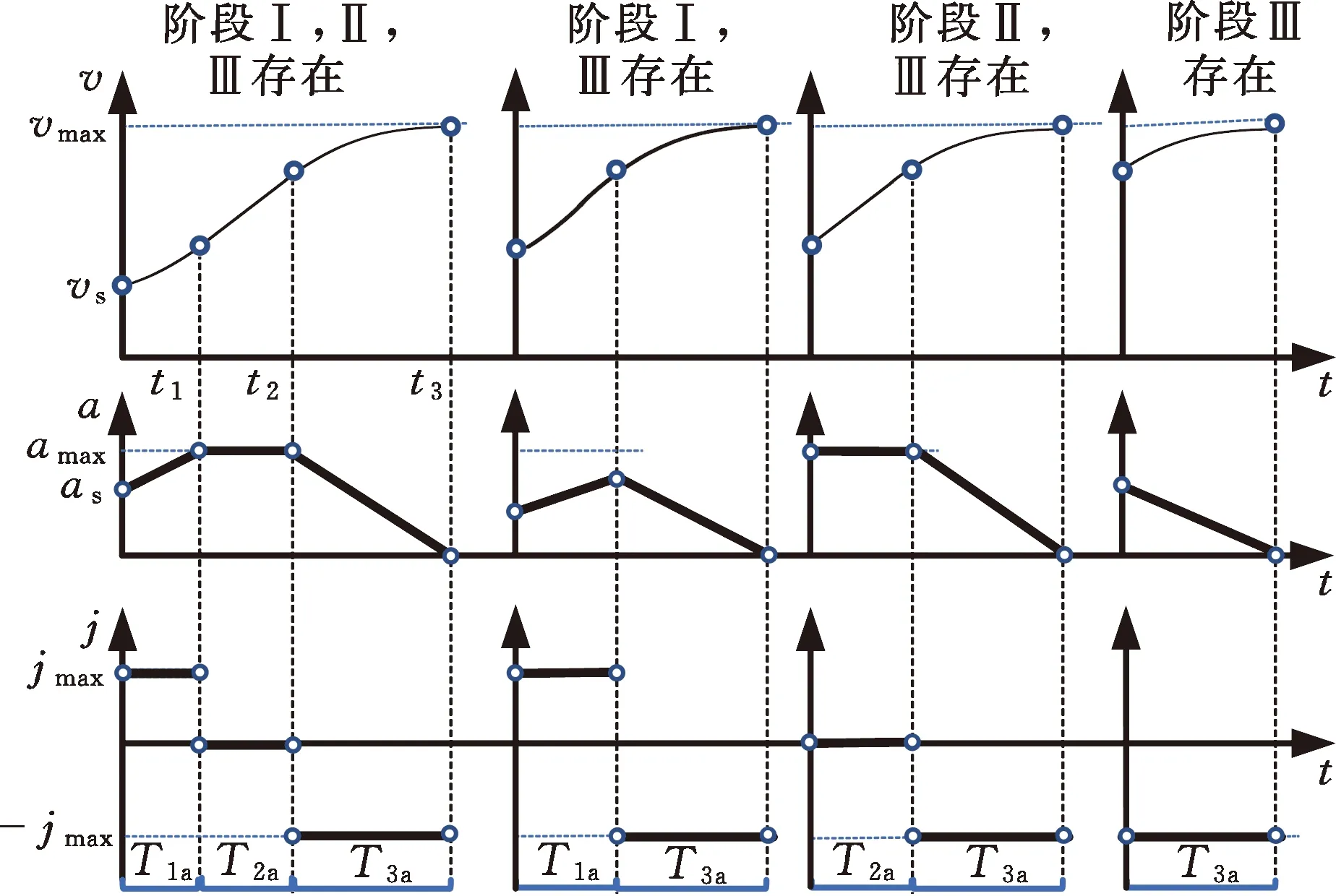
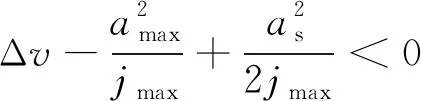
2 平面直線轉角非對稱平滑規劃建模
2.1 直線轉角的非對稱平滑規劃軌跡


2.2 非對稱直線轉角平滑規劃參數的確定

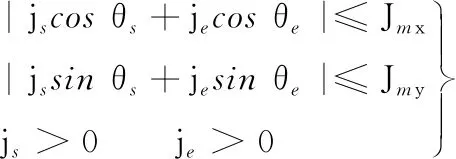
3 優化模型求解
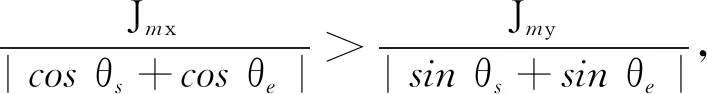
4 仿真分析與實驗驗證
4.1 單轉角對比分析
4.2 連續轉角對比分析



4.3 樣機實驗驗證


5 結語

