五相直線電機混合空間矢量脈寬調制控制策略

丁強，石滕瑞，鮑旭聰

(1.南京工業(yè)職業(yè)技術大學電氣工程學院，江蘇南京 210023；2.江蘇省風力發(fā)電工程技術中心，江蘇南京 210023；3.南京航空航天大學自動化學院，江蘇南京 210016)

0 前言

近幾年，隨著自動控制技術和微型計算機的高速發(fā)展，對各類自動控制系統(tǒng)的進給速度、加速度、快速定位精度等提出了更高的要求[1]。傳統(tǒng)旋轉電機加一套變換機構組成的直線運動驅動裝置已不再能滿足需求，而能夠實現直接直線傳動的直線電機，因省去中間轉換裝置，轉換效率高，是當前的研究熱點[2-3]。直線電機因起動推力大、動態(tài)響應快、定位精度高以及不存在傳統(tǒng)旋轉電機離心力的約束等優(yōu)點[4-5]，在交通運輸、數控機床、能源發(fā)電等領域已有廣泛應用。

由于永磁體勵磁不需要額外的繞組，可大幅度減小體積、節(jié)省成本[6]，永磁直線電機是當前應用最為廣泛的直線電機類型。永磁直線電機是一個多變量、非線性、強耦合性的復雜系統(tǒng)[7-8]，故高效高精度的控制策略是實現直線電機高性能驅動的前提。當前直線電機的控制方式主要有：恒壓頻比(V/f)控制[9]、直接推力控制[10]以及矢量控制[11-13]等。前兩者因控制精度不高、推力波動大，難以應用于高性能場合；矢量控制因較好的動態(tài)性能以及較高的控制精度，是當前直線電機最常用的控制方式。文獻[14]為實現基于矢量控制的直線電機系統(tǒng)高精度抗干擾在線多參數辨識，提出一種新型自適應互聯擴展卡爾曼觀測器，提高了系統(tǒng)的魯棒性。文獻[15]基于直線電機矢量控制系統(tǒng)，提出一種定位力補償二階自抗擾控制器，提升了直線電機位置控制的抗擾性能及跟蹤性能。文獻[16]針對直線電機伺服系統(tǒng)易受不確定因素干擾影響位置跟蹤精度問題，提出一種基于周期性擾動學習的自適應滑模控制方案，顯著提升系統(tǒng)的動態(tài)響應性能和魯棒性能，可以達到更高的位置精度。

為進一步提高推力密度，多相直線電機是今后的發(fā)展趨勢[17]。五相直線電機因高推力密度、強容錯能力以及較低的成本，是當前的研究熱點[18]。但與此同時，多相化帶來的拓撲結構復雜、系統(tǒng)諧波含量高以及控制算法復雜等問題，也對直線電機驅動系統(tǒng)提出了更高的要求[19-20]。

針對當前傳統(tǒng)五相直線電機單空間矢量脈寬調制控制策略運行性能差、系統(tǒng)諧波含量高的問題，本文作者首先搭建了五相直線電機離散域解耦控制數學模型，為后續(xù)控制算法優(yōu)化設計提供了基礎。其次，為抑制系統(tǒng)諧波，文中提出了一種五相直線電機雙混合空間矢量脈寬調制控制策略。為提高電壓利用率，所提策略在采用兩大電壓矢量的基礎上，引入額外2種電壓矢量，通過合理分配電壓矢量作用時間，達到抑制系統(tǒng)諧波的效果，提升電機運行性能。仿真與實驗均充分驗證了文中所提五相直線電機雙混合空間矢量脈寬調制控制策略的有效性及優(yōu)越性。

1 五相直線電機數字控制系統(tǒng)

為實現五相直線電機高性能運行，常采用空間矢量解耦控制策略，故五相直線電機離散化建模是搭建其數字控制系統(tǒng)的基礎。

1.1 五相直線電機連續(xù)域解耦控制數學模型

由于直線電機具有復雜多變的電感和磁鏈，具有強耦合關系，因此為方便研究，在搭建五相直線電機數學模型時作出了如下假設：

(1)不考慮鐵芯飽和、渦流、磁滯效應以及溫度變化對電機參數的影響；

(2)電機氣隙分布均勻；

(3)電機線圈繞組均勻分布在齒槽上。

由于五相直線電機多工作于電動機狀態(tài)，所以文中以電動機的標注慣例對數學模型中的各個參數進行標注，其中相電流的參考方向與相電壓的參考方向一致，與反電動勢的參考方向相反。靜止坐標系下的五相直線電機連續(xù)域數學模型主要包括：電壓方程、電磁推力方程以及機械運動方程，如式(1)—式(3)所示。

(1)

(2)

(3)

其中：U、I、e分別為相電壓、電流、反電動勢矩陣；R、L分別為相電阻、電感矩陣；v為電機運行速度；m為直線電機動子和負載的總質量；B為黏滯摩擦系數；Fm、FL分別為電磁推力、負載阻力。

為實現五相直線電機勵磁、推力解耦控制，需要搭建五相直線電機dq旋轉坐標系下數學模型。當前永磁電機的磁場定向控制策略常采用“id=0”的控制方案，基于此，五相直線電機dq旋轉坐標系下數學模型如式(4)和式(5)所示。

(4)

(5)

其中：ud、uq、id、iq分別為dq軸定子相電壓、電流；Rs為相等效電阻；Ld、Lq、ψd、ψq分別為dq軸相電感、磁鏈；ke為電機反電動勢系數；Δθ為反電動勢與電流的相位差。

1.2 五相直線電機離散化解耦控制數學模型

將式(3)—式(5)進行前向歐拉差分，可得到五相直線電機離散化解耦控制數學模型，如式(6)—式(8)所示。

(6)

(7)

(8)

其中：x(k)表示對應物理量k時刻的值；Ts為數字系統(tǒng)控制周期。

2 五相直線電機空間矢量脈寬調制策略優(yōu)化設計

給出五相直線電機單矢量空間脈寬調制策略詳細推導過程，并在此基礎上，提出一種五相直線電機優(yōu)化混合雙矢量空間脈寬調制策略，降低系統(tǒng)諧波含量，提高系統(tǒng)整體效率。

2.1 基準電壓空間矢量

五相逆變器一共有32種開關狀態(tài)，即存在32個電壓空間矢量，其基準電壓空間矢量分布如圖1所示。

由圖1可知，五相逆變器的32個基準電壓空間矢量將空間分成了均為36°的10個扇區(qū)，且其中30個非零矢量按照幅值大小可分為小矢量VS、中矢量VM和大矢量VL三大類，且大矢量的幅值為中矢量的1.618倍；中矢量的幅值為小矢量的1.618倍。

2.2 單空間矢量脈寬調制策略

為提高電壓利用率，單空間矢量脈寬調制策略一般采用2個大矢量合成參考電壓空間矢量，如圖2所示。

當參考電壓空間矢量所處扇區(qū)的扇區(qū)號為N時，假設該扇區(qū)順時針、逆時針方向基準電壓空間矢量(大矢量)作用時間分別為Ts1、Ts2。

圖2結合伏秒平衡原則，可得：

(9)

(10)

其中：θe為電機電角度。

將式(9)、式(10)聯立可計算得到：

(11)

即可得到基準電壓空間矢量的作用時間。

2.3 雙混合空間矢量脈寬調制策略

五相電機常采用星形連接形式，由于連接形式的限制，與傳統(tǒng)三相星形連接不同的是，五相電機的諧波含量會比較豐富，主要為三次諧波，故需要在考慮三次諧波的基礎上，對空間矢量脈寬調制策略進行優(yōu)化設計。

五相逆變器三次諧波坐標系下的基準電壓空間矢量如圖3所示。

統(tǒng)一開關狀態(tài)下，由圖1及圖3可知：

(1)在基波坐標系下對應的基準電壓空間矢量幅值為大矢量而在三次諧波坐標系下為小矢量；

(2)在基波坐標系下對應的基準電壓空間矢量幅值為中矢量在三次諧波坐標系下仍為中矢量。

故可利用上述基準電壓空間矢量雙坐標系下的對應關系，在單空間矢量脈寬調制的基礎上，引入額外基準電壓空間矢量，合理分配矢量，可達到抑制諧波的效果。

為提高電壓利用率，文中采用雙混合空間矢量脈寬調制方案，引入額外的中矢量，如圖4所示，合理分配大矢量與中矢量的作用時間，以達到抑制五相直線電機三次諧波的效果。當參考電壓空間矢量所處扇區(qū)的扇區(qū)號為N時，假設該扇區(qū)順時針方向基準電壓空間矢量大矢量、中矢量的作用時間分別為Td1、Td2；逆時針方向基準電壓空間矢量大矢量、中矢量的作用時間分別為Td3、Td4。

由圖4結合伏秒平衡原則，可得：

(12)

(13)

以第一扇區(qū)為例，在基波坐標系下的大、中矢量到三次諧波坐標系下成為小、中矢量，其對應關系如圖5所示。

由圖5可知，當基波坐標系下大矢量和中矢量的作用時間滿足以下關系時：

(14)

4個基準電壓矢量在三次諧波坐標系中合成電壓空間矢量為0，即可達到抑制三次諧波的效果。

將式(12)—式(14)聯立可得：

(15)

2.4 基于空間矢量脈寬調制策略的五相直線電機控制系統(tǒng)

文中采用五相直線電機控制結構框圖如圖6所示，是一個基于空間矢量脈寬調制控制策略的速度、電流雙閉環(huán)控制系統(tǒng)。其中，空間矢量脈寬調制策略可采用傳統(tǒng)單空間矢量脈寬調制策略方案，或文中所提雙混合空間矢量脈寬調制策略方案。

3 仿真與實驗

3.1 MATLAB/Simulink仿真結果及分析

對圖6所示的五相直線電機雙閉環(huán)解耦控制系統(tǒng)進行不同空間矢量脈寬調制策略方案的仿真驗證，五相直線電機參數如表1所示。

表1 電機參數

MATLAB/Simulink仿真參數如表2所示。

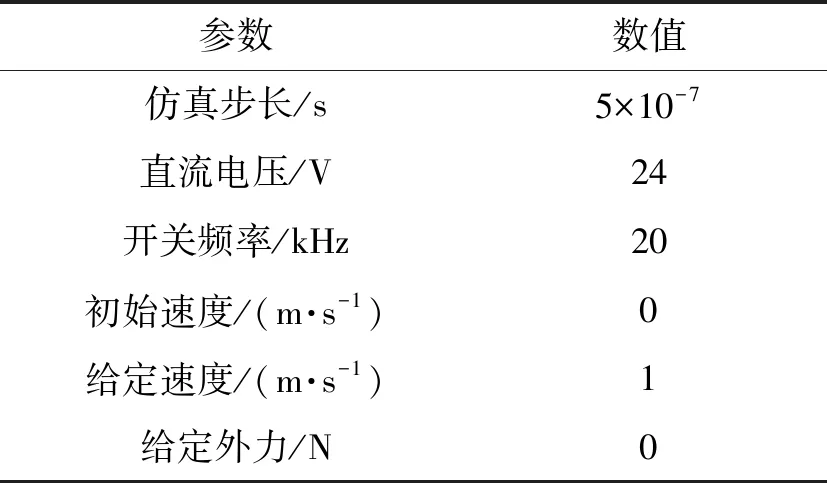
表2 仿真參數

對單矢量SVPWM算法與混合矢量SVPWM算法分別進行仿真，開關頻率皆設置為20 kHz，五相直線電機相電流波形如圖7所示，各相電流相位互差2π/5。

取五相中A相相電流如圖8所示。可知:單矢量下相電流為削頂正弦波，即諧波含量較高；而混合矢量下相電流正弦度較好。相電流幅值前者在0.95 A左右，后者在1.05 A左右，電流頻率二者相同，皆為125 Hz，與理論情況相符。

對2種算法下直線電機相電流分別進行快速傅氏變換(Fast Fourier Transform，FFT)分析，結果如表3所示。可知:單矢量SVPWM控制下的相電流總諧波失真(Total Harmonic Distortion，THD)數值約是混合矢量下的15倍;而單矢量SVPWM控制下的相電流諧波含量中絕大部分為三次諧波，相對基波分量的含量為19%。

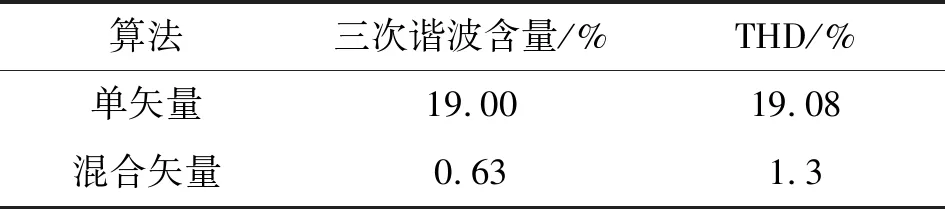
表3 相電流諧波分析數據

2種SVPWM算法控制下直軸電流id波形如圖9所示，id最終穩(wěn)定在0附近，與理論情況相符。單矢量下，id峰值約為0.087 A，在0.006 s左右進入穩(wěn)態(tài)，穩(wěn)態(tài)時有幅值約為0.006 A的脈動; 混合矢量下，id峰值約為0.29 A，在0.019 s左右進入穩(wěn)態(tài)，穩(wěn)態(tài)時有幅值約為0.007 A的脈動。相較而言，單矢量下的id波形稍好一些。

同樣，作出交軸電流iq波形如圖10所示，iq最終都穩(wěn)定在恒值1.05 A附近，此值大小與外加推力FL有關，符合理論情況。單矢量下，iq峰值約為1.667 A，在0.031 s左右進入穩(wěn)態(tài)，穩(wěn)態(tài)時有幅值約為0.007 A的脈動; 混合矢量下，iq峰值約為1.2 A，在0.013 s左右進入穩(wěn)態(tài)，穩(wěn)態(tài)時有幅值約為0.007 A的脈動。相較而言，混合矢量下的iq波形較好一些。

在空載運行條件下，2種算法電磁推力波形如圖11所示，Fm最終穩(wěn)定在恒值0.03 N附近，因為電機本身存在一定阻力，故穩(wěn)態(tài)時電磁推力會略大于外加負載力，不為零。單矢量下，Fm峰值約為0.048 N，在0.004 5 s左右進入穩(wěn)態(tài)，穩(wěn)態(tài)時有幅值約為0.000 6 N的脈動; 混合矢量下，Fm峰值約為0.034 5 N，在0.008 s左右進入穩(wěn)態(tài)，穩(wěn)態(tài)時有幅值約為0.000 43 N的脈動。可見，混合矢量下的電磁推力快速性稍差一些，但脈動比單矢量下的小一些。

電機運行速度v在不同SVPWM算法下的波形如圖12所示，經過一段時間后，v最終都穩(wěn)定在1 m/s，即給定轉速，符合理論情況。單矢量下，v峰值約為1.04 m/s，在0.003 s左右進入穩(wěn)態(tài)，穩(wěn)態(tài)時有幅值約為0.000 52 m/s的波動; 混合矢量下，v峰值約為1.016 6 m/s，在0.007 s左右進入穩(wěn)態(tài)，穩(wěn)態(tài)時有幅值約為0.000 35 m/s的波動。可見，混合矢量下的運行速度穩(wěn)態(tài)波動比單矢量下的更小。

對上述2種SVPWM算法從電流紋波、諧波含量角度分析總結可得：單矢量SVPWM算法控制下電流諧波含量很高，主要為三次諧波；混合矢量SVPWM算法不僅電流紋波小，且諧波含量低，對三次諧波有明顯的抑制效果，控制效果更佳。

3.2 硬件實驗結果及分析

文中采用基于DSP的五相直線電機驅動器，五相直線電機如圖13所示，電機實驗參數與仿真參數一致。

五相直線電機驅動器總體結構框架如圖14所示。驅動器控制芯片采用TI公司的TMS320F2812，主要負責五相直線電機的數字控制與算法實現。

分別用單矢量SVPWM算法和混合矢量SVPWM算法驅動五相直線電機。設置電機空載運行，運行速度為1 m/s，此種工況下直線電機相電流波形如圖15所示。可知：電流頻率二者相同，約為125 Hz，單矢量下電流波形畸變嚴重，電流峰值達到2 A左右；而混合矢量下電流波形正弦度較好，電流幅值約為1 A，與理論及仿真結果一致。

2種算法控制下相電流FFT分析如圖16所示。可得：單矢量SVPWM控制下的相電流THD數值較大，而混合矢量控制下則比較小，前者約是后者的5.5倍；單矢量SVPWM控制下的相電流諧波含量中絕大部分為三次諧波，約占諧波總量的86.7%，而混合矢量SVPWM算法下相電流三次諧波含量較小；其他次諧波含量2種算法控制下都差不多。說明五相直線電機中三次諧波問題嚴重，而混合矢量SVPWM算法抑制三次諧波具有較好效果。

4 結論

針對五相直線電機傳統(tǒng)單空間矢量脈寬調制控制策略運行性能差、系統(tǒng)諧波含量高的問題，文中提出一種雙混合空間矢量脈寬調制策略。為提高電壓利用率，所提方案引入額外的中矢量，通過合理分配大矢量與中矢量的作用時間，以達到抑制五相直線電機三次諧波的效果。仿真與實驗結果表明：與傳統(tǒng)單空間矢量脈寬調制策略相比，使用文中所提雙混合空間矢量脈寬調制策略方案的五相直線電機系統(tǒng)諧波含量明顯降低，提高了系統(tǒng)效率，且電機運行性能得到顯著提升。