HDPE膜焊接機器人熱力機電耦合能域系統動力學全解建模

陳亞宇， 陳鑫宇， 郭 菲， 孟彩茹， 張 超， 陳 月

(1. 河北工程大學 機械與裝備工程學院， 河北 邯鄲 056038； 2. 河北工程大學 圖書館， 河北 邯鄲 056038；3. 河北建設集團安裝工程有限公司， 河北 保定 071000)

在垃圾填埋場運營中，由于地基不均勻下陷、機械破損、化學腐蝕、縮性形變等原因會引起防滲高密度聚乙烯(high density polyethylene，HDPE)膜破損[1]。如果漏洞沒有被及時修補，會嚴重污染周圍土壤及地下水[2]。目前針對運營中垃圾填埋場漏洞修補主要是灌漿修補法，但該方法由于卵石層間隔不規律、高分子灌漿材料的不穩定性[3-4]，可能發生灌漿材料未到達HDPE膜破損部位凝固的現象，使其修補效果欠佳。

針對上述問題，本文提出利用并聯焊接機器人，在前期破損定位基礎上，利用鉆探技術移除膜上介質后，對裸露HDPE膜直接焊接修補的方法。所研究的并聯焊接機器人將并聯機構和熱熔焊加工結合起來，具備剛度高、動力學性能好、結構緊湊[5-7]及熱熔焊精準焊接HDPE膜破損等優勢，能有效彌補灌漿修補不確定因素。

目前應用于多剛體系統動力學的方法主要有以下幾種：牛頓-歐拉法[8-9]、拉格朗日方程法[10-11]、凱恩法[12-13]、虛功原理[14-15]等。以上方法被廣泛用于并聯機器人動力學建模中，但局限于單能域動力學建模，若要構建多能域動力學模型，需利用中間變量將各個子能域分別建模列動力學方程并聯立求解，不僅增加了方程數目，還導致計算過程繁瑣。因此，文獻[16-17]中，提出了旋量鍵合圖理論，將旋量理論[18]和鍵合圖[19]相結合，利用旋量理論分析空間機構簡潔的優勢，有效降低了傳統鍵合圖分析空間機構動力學復雜性[20]。鍵合圖理論作為一種圖形化建模工具，在熱力學工程領域得到了廣泛應用[21-23]。本文采用旋量鍵合圖建立并聯機構本體系統動力學模型，采用傳統鍵合圖建立伺服電機驅動和熱力子系統鍵合圖模型，獲得完整的機、電、熱耦合多能域系統動力學全解模型。

1 HDPE膜焊接機器人機構簡介

本文研究的HDPE膜焊接機器人由X4并聯機器人[24]動平臺輸出軸上添加熱熔焊接裝置組成。文獻[25]運用螺旋理論對X4并聯機器人進行了自由度分析，其為三移一轉四自由度機構，具體的運動形式為沿空間3個軸線的任意平動及繞垂直動平臺軸線的轉動，能夠滿足HDPE膜焊接的需要。該并聯機器人機構簡圖，如圖1所示，其定平臺上4個轉動副R的鉸點用A1，A2，A3和A4表示,A1A3與A2A4兩線相互垂直，動平臺上4個轉動副R的鉸點用D1，D2，D3和D4表示，D1D3與D2D4兩線夾角χ為120°，定平臺和動平臺通過4條完全相同的R-(2-SS)-R支鏈相連，伺服電機和減速器轉動驅動主動臂AiBi(i=1,2,3,4)，從動臂由平行四邊形4S通過另一個轉動副與動平臺相連。在定平臺上建立定坐標系O-XYZ，即慣性坐標系ΨO,坐標原點O位于轉動副(A1，A2，A3，A4)所在平面的幾何中心,X軸垂直于A1A2，Y軸垂直于A2A3,Z軸為過中心點O的豎直軸。同樣建立動坐標系o-xyz，坐標原點o位于轉動副(D1，D2，D3，D4)所在平面的幾何中心，x軸垂直于D1D2,y軸垂直于D2D3,z軸為過中心點o的豎直軸。末端執行部分的焊接裝置采用熱熔焊槍，HDPE膜焊接機器人的三維模型，如圖2所示。

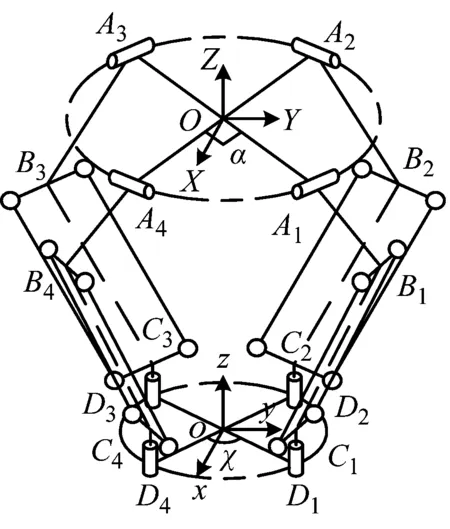
圖1 X4機器人機構簡圖Fig.1 Mechanism diagram of X4 robot

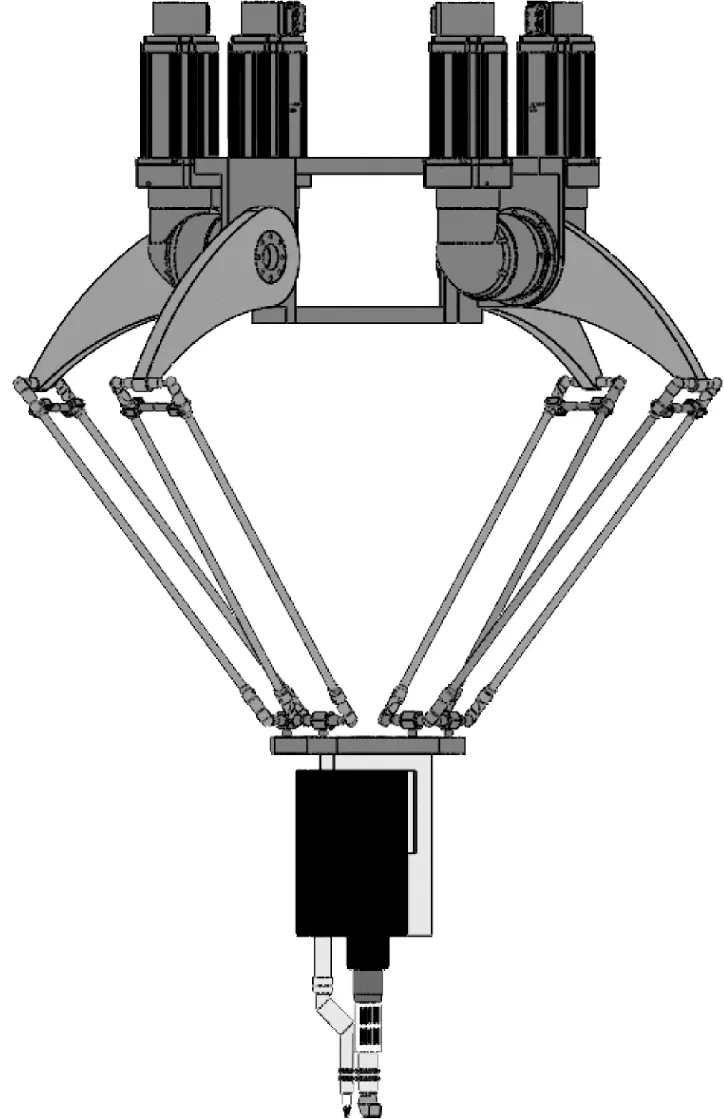
圖2 HDPE膜焊接機器人三維模型Fig.2 3D model of HDPE film welding robot

2 HDPE膜焊接機器人動力學建模

2.1 機器人機械本體建模

2.1.1 支鏈旋量鍵合圖建模

由于X4并聯機器人具有4條結構相同的支鏈，選取第i條支鏈進行建立支鏈坐標系，其結構如圖3所示。

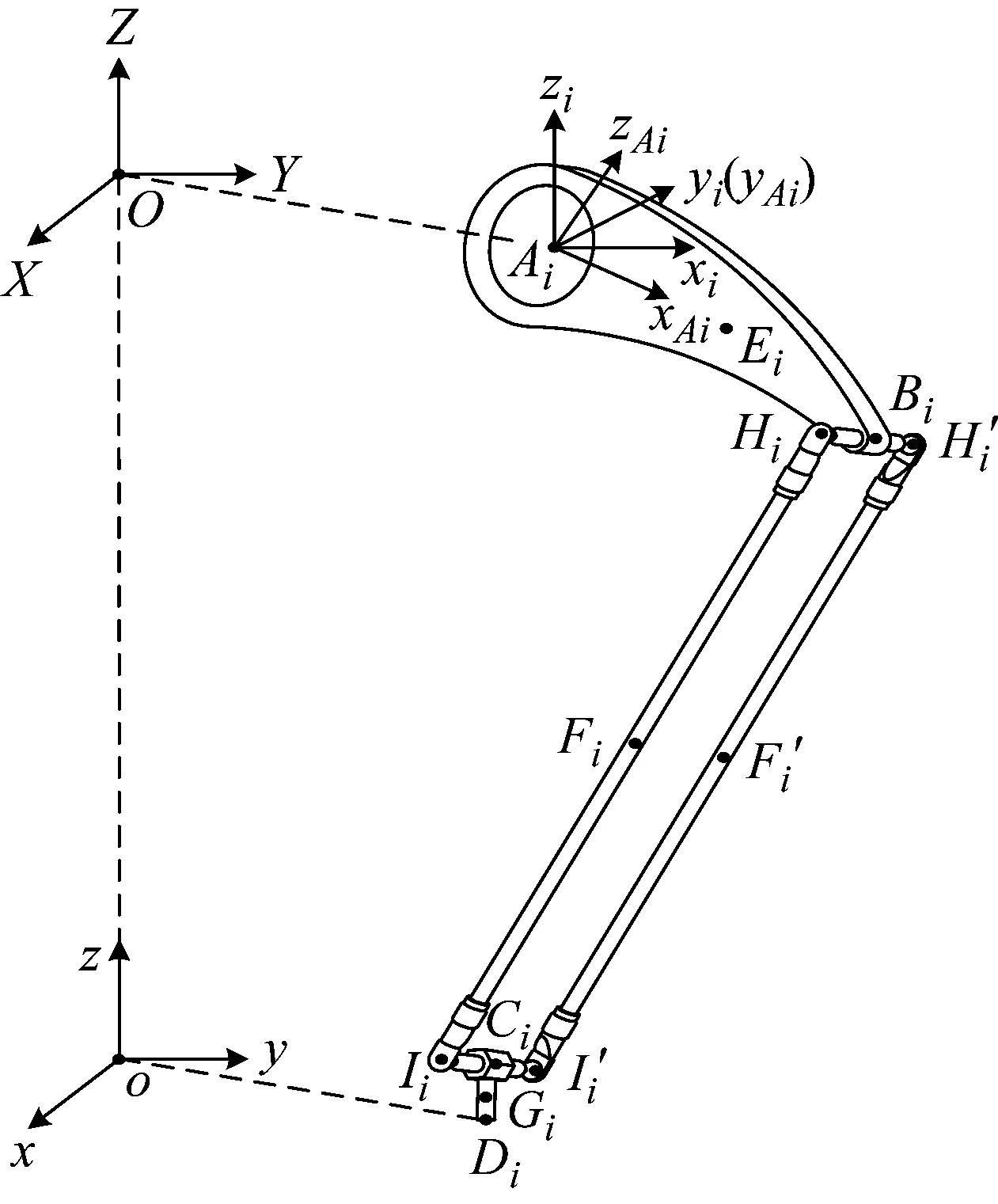
圖3 第i條支鏈結構圖Fig.3 Structure diagram of the ith chain

建立支鏈旋量鍵合圖建模所需的坐標系為以下。

支鏈坐標系：以轉動副轉動中心Ai為坐標原點，建立支鏈坐標系Ψi,其zi軸為平行于慣性坐標系Z方向，yi軸為轉動副固定軸線方向，則xi=yi×zi。

輔助坐標系：以主動臂Bi點為坐標原點，建立輔助坐標系ΨBi，其xBi軸方向平行于BiCi方向向量，zBi軸垂直于四球鉸副轉動中心所定義的平行四邊形平面，則yBi=xBi×zBi。

運動副接觸坐標系：首先，建立轉動副接觸坐標系ΨAi,以轉動中心Ai為坐標原點，其zAi軸方向平行于AiBi方向向量，yAi軸為轉動副固定軸線方向，則zAi=xAi×yAi。其次，建立轉動副接觸坐標系ΨDi和球鉸副接觸坐標系ΨHi，ΨH′i，ΨIi，ΨI′i，分別以轉動副轉動中心Di和球鉸副轉動中心Hi，H′i，Ii，I′i為坐標原點，ΨDi坐標軸方向平行于慣性坐標系ΨO的各坐標軸方向，其余球鉸副接觸坐標軸方向平行于輔助坐標系ΨBi的各坐標軸方向。

桿件質心坐標系：在4個連桿的質心位置處分別建立四連桿的質心坐標系ΨEi，ΨFi，ΨF′i，ΨGi，其中質心坐標系ΨEi與接觸坐標系ΨAi平行，質心坐標系ΨGi與慣性坐標系ΨO平行，其余質心坐標系與輔助坐標系ΨBi平行。

根據郭菲等的研究建立支鏈旋量鍵合圖，如圖4所示。由于轉動副Ai連接定平臺，速度為0，故采用0流源輸入。轉動副Di連接動平臺，通過鍵②/③/④/⑤，將支鏈旋量鍵合圖連接到動平臺旋量鍵合圖,可得到該并聯機構完整旋量鍵合圖模型。鍵①表示連接到電機驅動子系統鍵合圖。

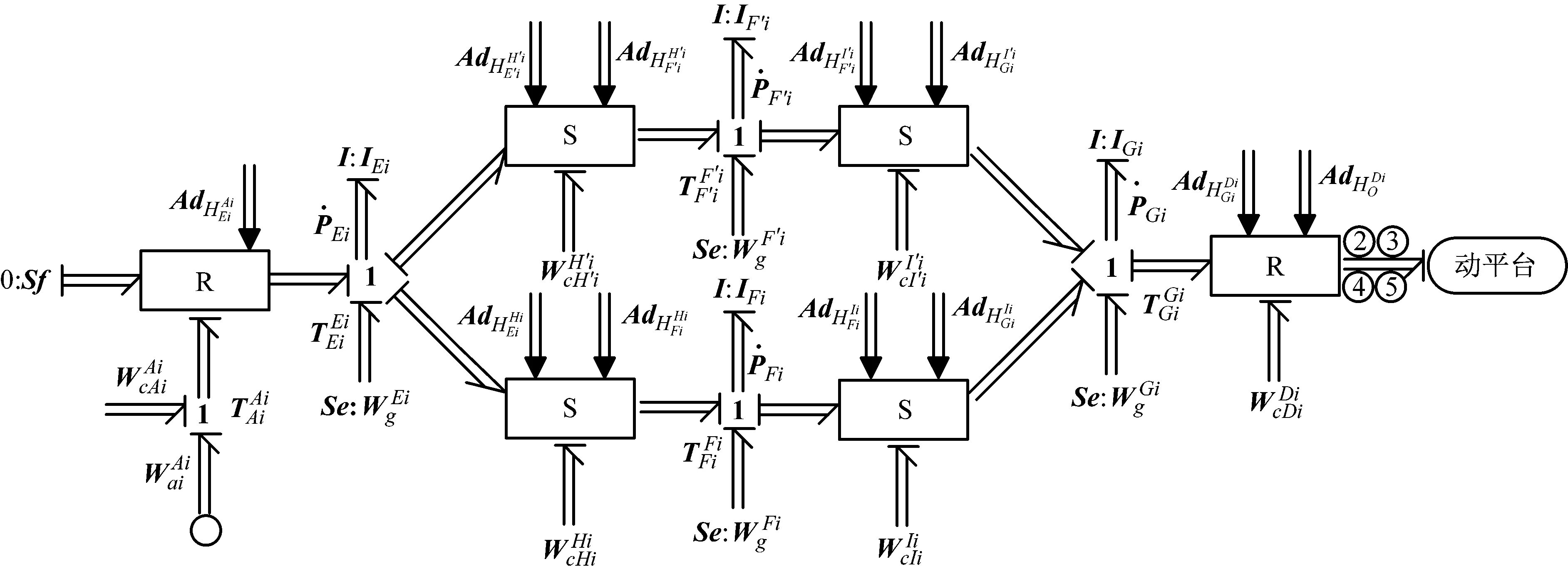
圖4 支鏈i旋量鍵合圖Fig.4 Screw bond graph of the i chain

根據支鏈旋量鍵合圖模型，列出支鏈狀態方程為

(1)

其中

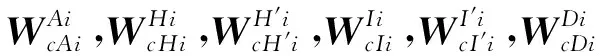
2.1.2 動平臺旋量鍵合圖建模

首先假設動平臺的E點受到We的載荷作用，以E點為坐標原點，建立與慣性坐標系ΨO平行的載荷坐標系Ψe，然后在動平臺質心位置建立與慣性坐標系ΨO重合的質心坐標系ΨP,如圖5所示。建立動平臺旋量鍵合圖，如圖6所示。

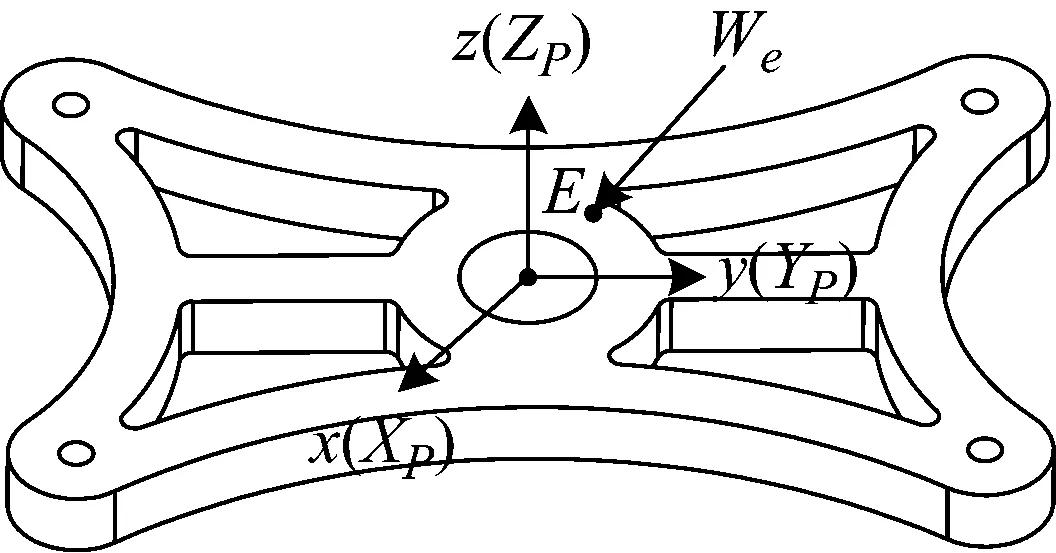
圖5 動平臺結構圖Fig.5 Structure diagram of moving platform

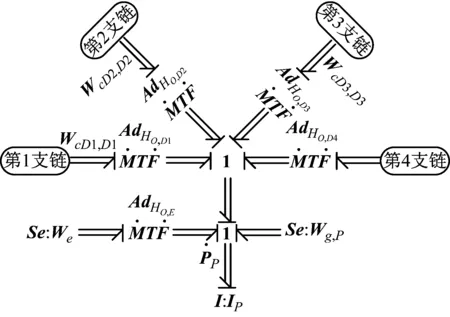
圖6 動平臺旋量鍵合圖Fig.6 Screw bond graph of moving platform

根據動平臺旋量鍵合圖模型，可列出動平臺狀態方程為

(2)

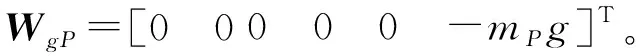
根據式(1)、式(2)聯立可得到機構本體動力學模型，共包含92個未知數，可列得92個相互獨立的方程，可求得驅動力和各構件之間約束力。

2.2 驅動電機鍵合圖建模

本文的并聯機器人采用伺服電機和減速器作為驅動設備，其鍵合圖模型如圖7所示。

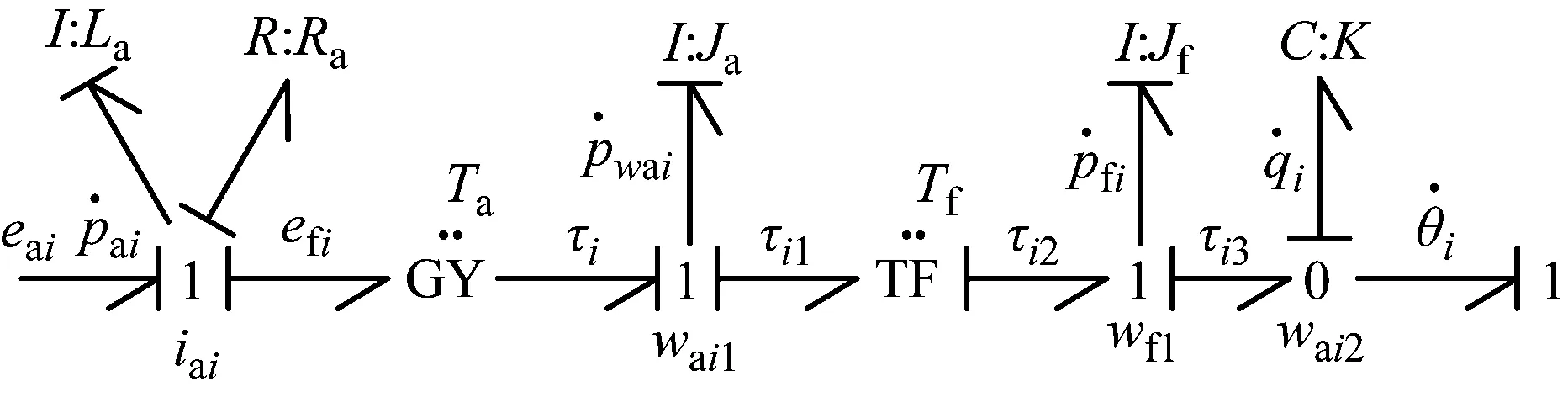
圖7 伺服電機和減速器鍵合圖模型Fig.7 Bonding graph model of Servo motor and reducer

分別選取電勢p和電流q作為狀態變量，可得到驅動系統的狀態方程為

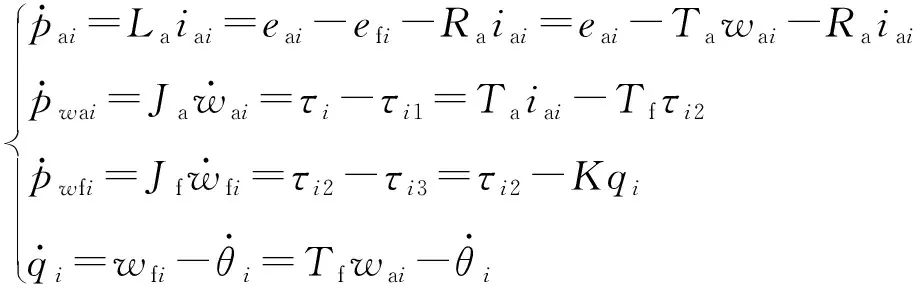
(3)

式中：La為電機電樞電感；Ra為電機電樞電阻；Ja為電機轉子的轉動慣量；Ta為電機電磁轉矩常數；Tf為減速器減速比；Jf為減速器轉子的轉動慣量；K為減速器扭矩剛度。

2.3 焊槍鍵合圖建模

熱風擠出焊槍主要由焊接驅動單元、熔化室、預熱室三部分構成，如圖8所示。熱風擠出焊槍是一個熱力和機電系統相耦合的動力裝置，其工作過程中涉及動力學、熱力學、傳熱學等諸多方面，由于熱力學復雜性，很難與其他能域鍵合圖模型直接耦合，為得到熱力機電系統耦合模型，本文基于變質量熱力系統基本方程簡化焊槍整體為一個三通口C-場并對其進行鍵合圖建模，用于分析其動力學與熱力學性能。

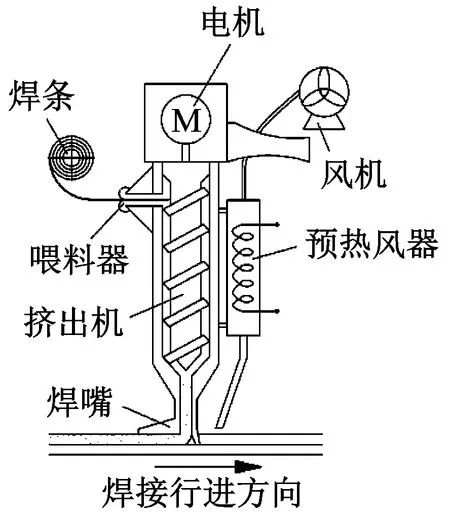
圖8 熱風擠出焊槍結構圖Fig.8 Structure diagram of hot air extrusion welding gun

吉布斯方程顯示內能變化可由3種能量作用表示，其表達式為式(4)，變質量熱力系統鍵合圖模型為圖9所示。

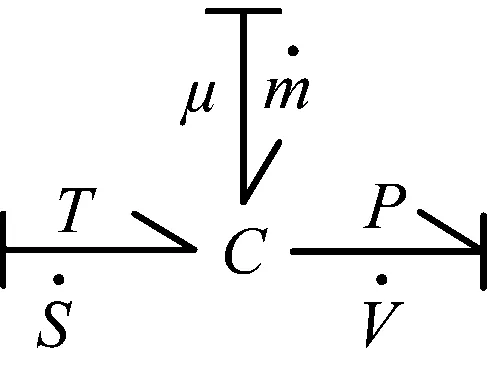
圖9 變質量熱力系統鍵合圖模型Fig.9 Bonding graph model of variable mass thermodynamic system

dU=TdS-PdV+μdm

(4)

式中：U為系統的內能；T為溫度；S為熵；P為壓力；V為體積；μ為吉布斯勢；m為質量。

根據變質量熱力系統的基本方程和理想氣體的狀態方程，可得出三通口C-場的特性方程[26]為

式中：v為工質的比體積；s為工質的比熵；h為比焓；T0，P0，v0，s0分別為各量的初始值；k為絕熱指數，k=cP/cV，cP為質量定壓熱容，cP=1.004 kJ/kg·K；cV為質量定容熱容，cV=0.717 kJ/kg·K。

焊接驅動單元建模：焊接驅動單元是由驅動電機帶動螺桿轉動，焊條通過喂料器喂入螺桿內部。由于直流電機的轉矩方程和電壓與伺服電機相同，故此處驅動電機建模與上述伺服電機建模相同。此處將焊料流入簡化為流源處理。

預熱室建模：預熱室中風機產生氣體并經過預熱風器進行加熱生成熱空氣：一部分從前端噴出用以對待焊接母材進行預熱；另一部分噴入熔化室，將螺桿內部重新塑化的焊料壓送到已加熱的待焊接材料表面。假設鼓風機中無回轉器，轉速恒定，將鼓入空氣作為流源處理。電熱電阻器鍵合圖模型如圖10所示，其中電熱和熱傳導的R-場特性方程分別為式(8)、式(9)。

圖10 電熱電阻器鍵合圖模型Fig.10 Bonding graph model of thermistor

式中：R=R25[1+α(T1-298)]，R25為25 ℃時的電阻值，α為溫度系數；T1，T2為熱傳導過程的絕對溫度，且T1-T2>0；H為熱傳導系數。

熔化室建模：在熔化室內，焊料被均勻熔化攪拌，重新塑合后擠出，將焊料流出簡化為流源處理。

焊槍工作過程中存在著機械功、熱傳遞、質量遷移3種能量變化，由鼓風機流入預熱室的新鮮空氣帶入能量，熱電阻絲加熱后又加入能量，總能量的一部分進入熔化室，熔化焊料，另一部分通過預熱噴嘴對待焊件進行預熱，其余部分留在預熱室轉化為內能。將上述的焊槍各部分鍵合圖通過C-場T，μ端口的0-結連接起來，得到焊槍多能域鍵合圖模型如圖11所示。

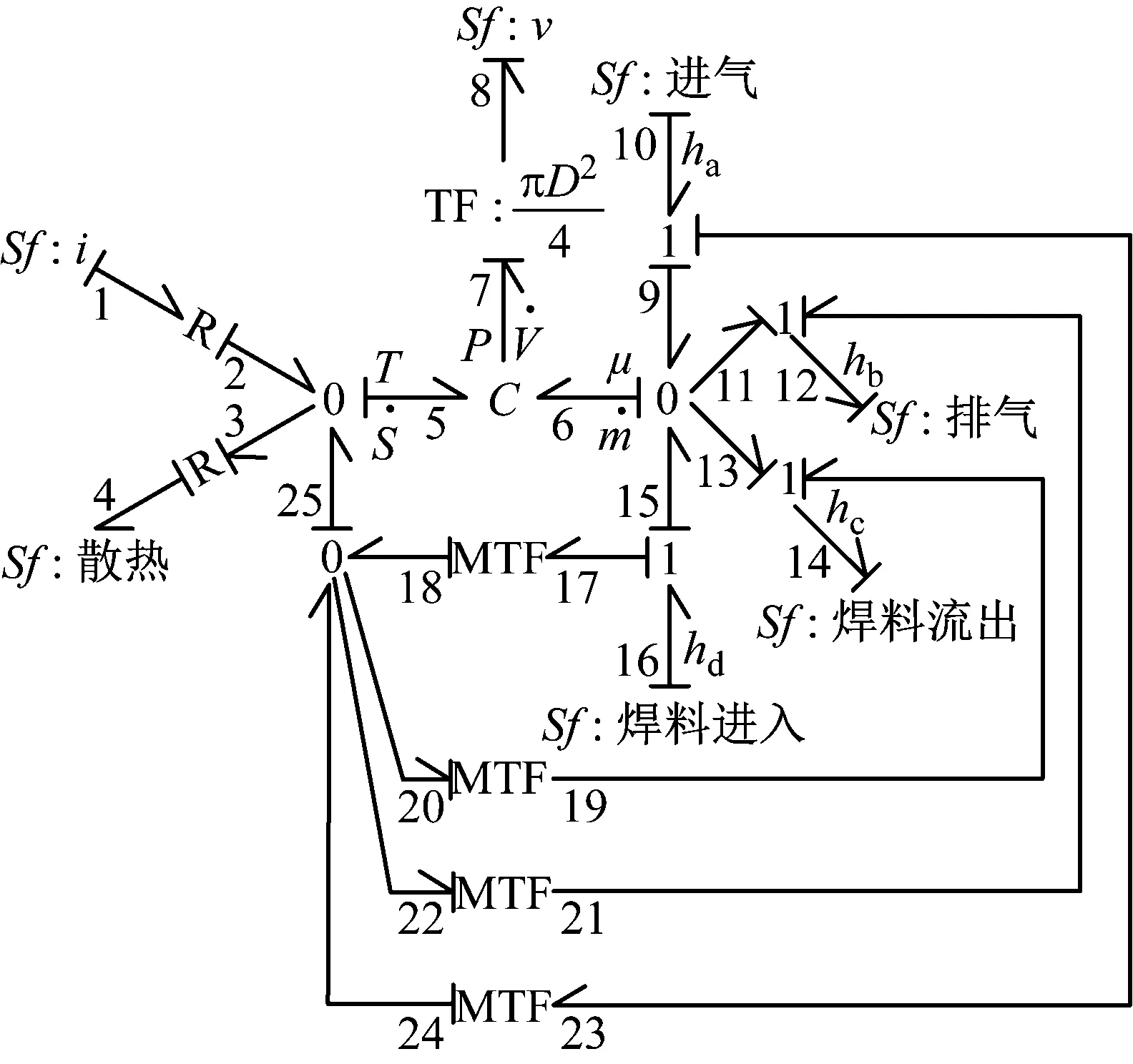
圖11 焊槍鍵合圖模型Fig.11 Bonding graph model of welding gun

系統輸入源是f1，f4，f8，f10，f12，f14，f16,狀態變量是q5(熵S)，q6(質量m)，q7(體積V)，可推導出狀態方程為

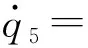
(10)

(11)

(12)

根據功率守恒，可得式中MTF17;18，MTF20;19，MTF22;21，MTF23;244個功率換能器的模數為

式中，ha，hb，hc，hd分別為流入空氣、排出空氣、流入焊料、排出焊料的比焓。

結合系統輸入源的邊界條件，聯立式(5)～式(16)，可解得其焊槍系統的動態特性。

2.4 焊接機器人多能域系統動力學全解模型

將驅動電機鍵合圖與并聯機器人旋量鍵合圖模型通過1-結相連，為保證焊槍焊接速度與機器人行走速度匹配，將機器人旋量鍵合圖與熱風擠出焊槍鍵合圖通過二通口-MTF-相連，建立HDPE膜焊接機器人機、電、熱耦合能域系統動力學全解模型，如圖12所示。

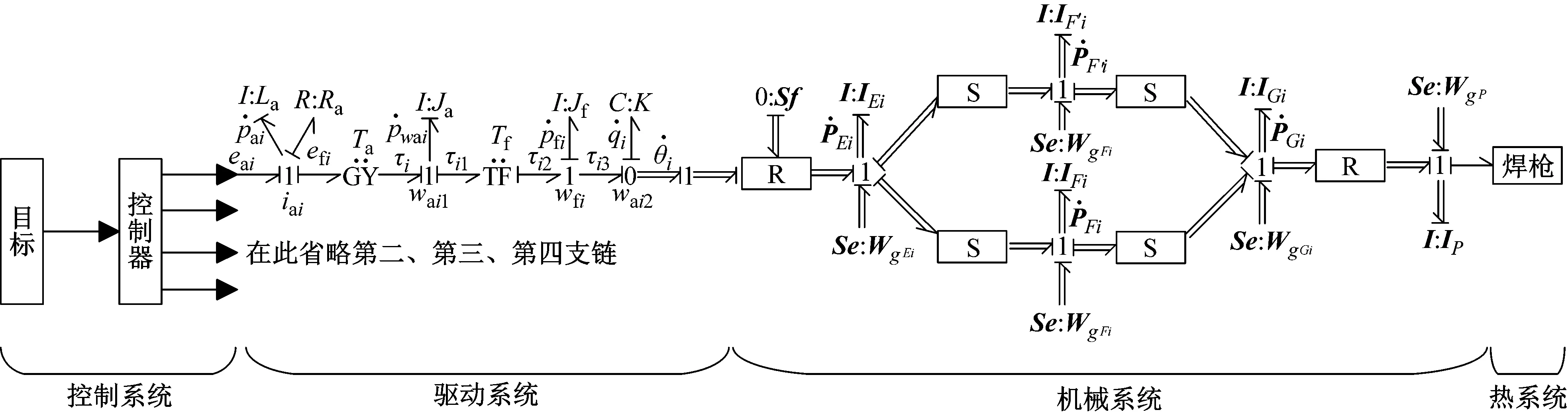
圖12 HDPE膜焊接機器人系統鍵合圖模型Fig.12 Bonding graph model of HDPE film welding robot system

根據焊接速度與行走速度成等比變化，可推得MTF的轉換模數為

M(v)=I/f

(17)

式中：I為焊接電流；f為擺動頻率。

基于系統全解鍵合圖模型，能直接獲得系統中各部件與部件間的運動、功率、溫度等信息。

3 仿真分析

3.1 并聯機構動力學全解仿真

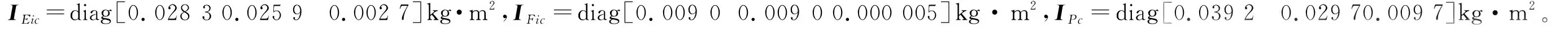
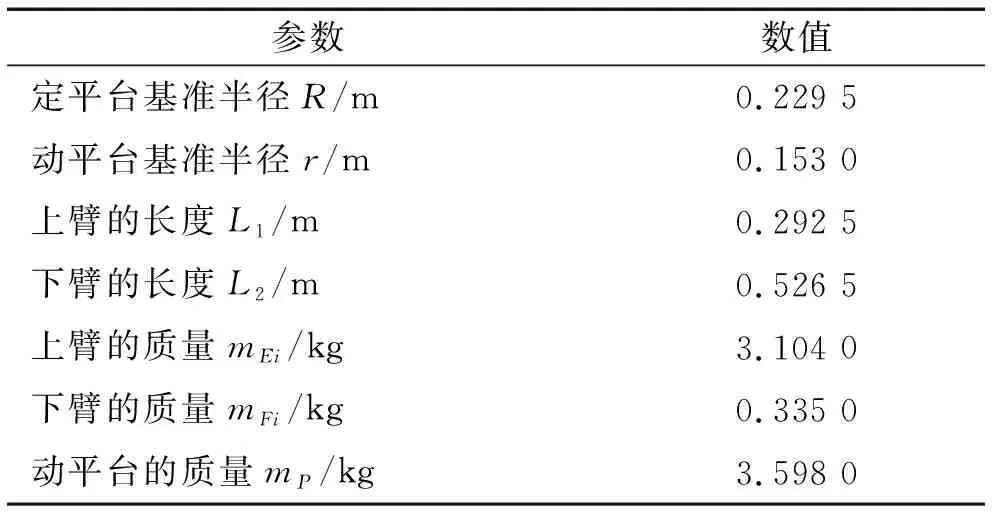
表1 并聯機構部分參數Tab.1 Part of parallel mechanism parameters

給定機構初始姿態為γ=0°，同時給動平臺施加一個50 N載荷，動平臺末端執行軌跡為:從原點出發沿x軸正方向移動100 mm,然后以原點O為圓心，半徑100 mm繞圓心旋轉一周。利用ADAMS軟件對建立的三維仿真模型進行仿真，仿真驗證模型如圖13所示，得到機構的仿真驅動力和約束力曲線，如圖14～圖17所示。同時通過機構的狀態方程和運動學信息，利用MATLAB軟件編程可以得到機構的理論驅動力矩曲線，如圖18所示。驅動力矩仿真值與理論值的誤差如圖19所示，其誤差來源主要為理論計算時忽略了球鉸等構件的慣量，最大誤差為0.29%，誤差相對于驅動力矩數值很小，因此可驗證基于旋量鍵合圖進行動力學建模的可靠性。

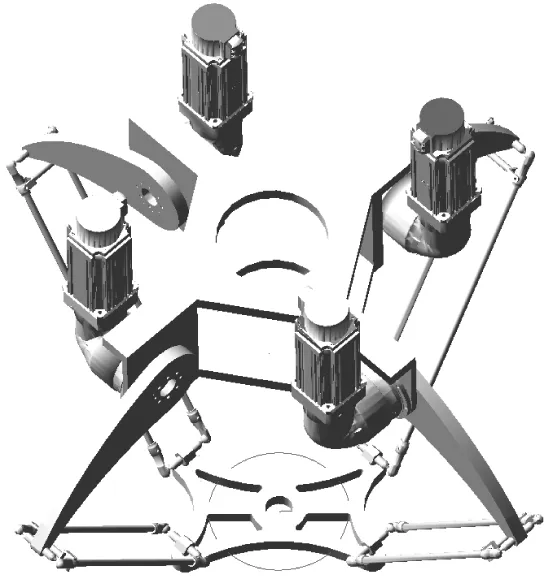
圖13 ADAMS仿真模型Fig.13 Simulation mode in ADAMS

圖14 仿真驅動力矩Fig.14 Driving torque of simulation

圖15 轉動副Ai處約束力Fig.15 Constraint force of the Ai rotation joints

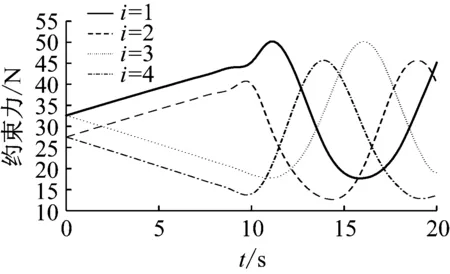
圖16 轉動副Di處約束力Fig.16 Constraint force of the Di rotation joints

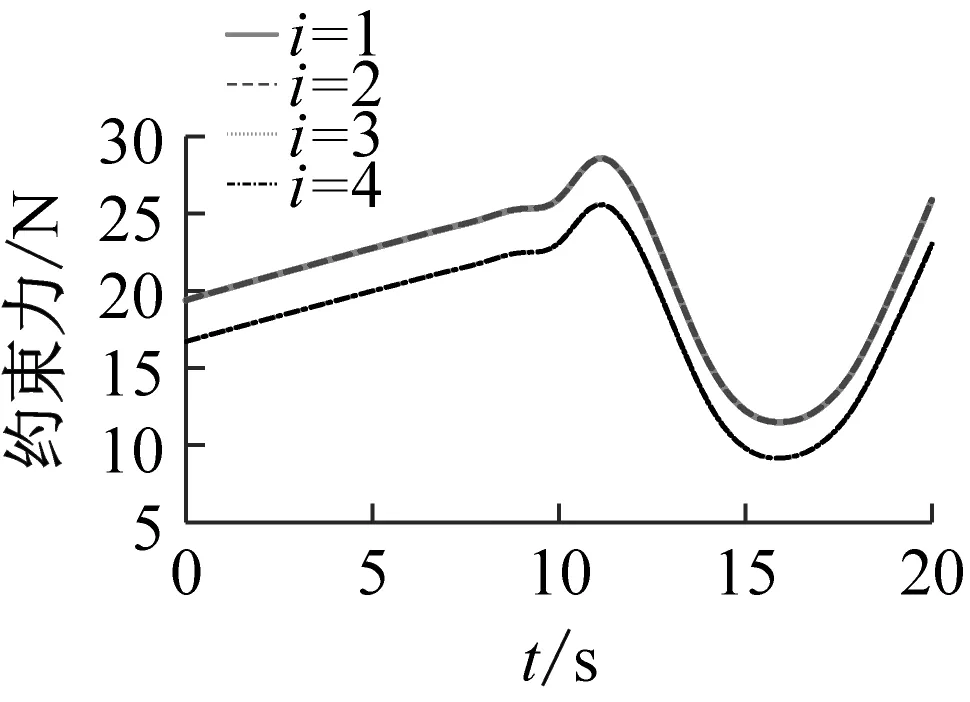
(a) 支鏈1

(b) 支鏈2

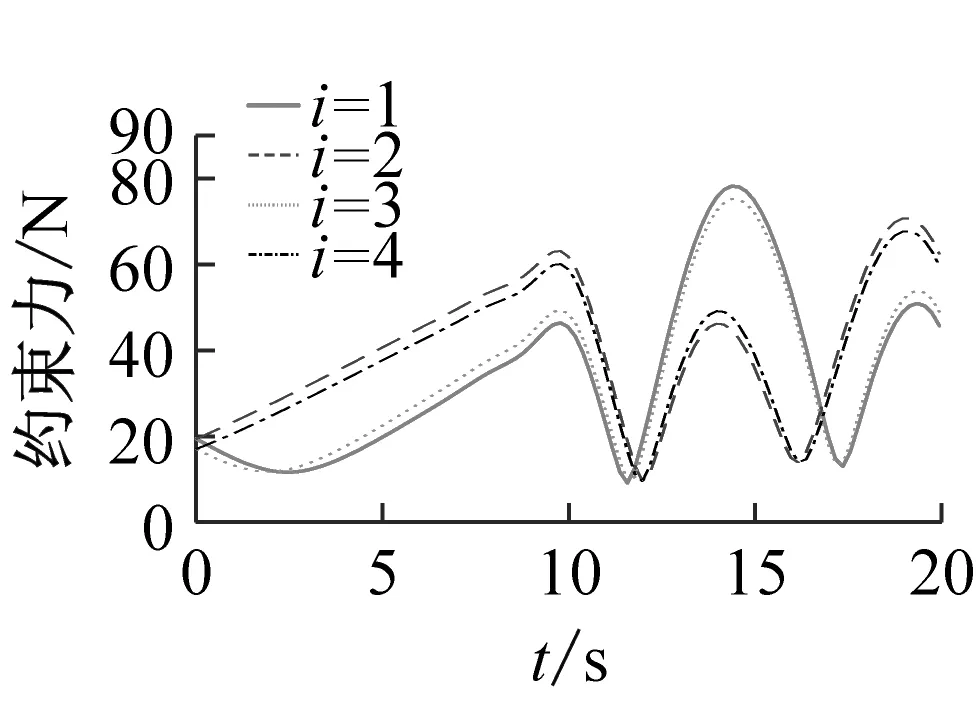
(c) 支鏈3

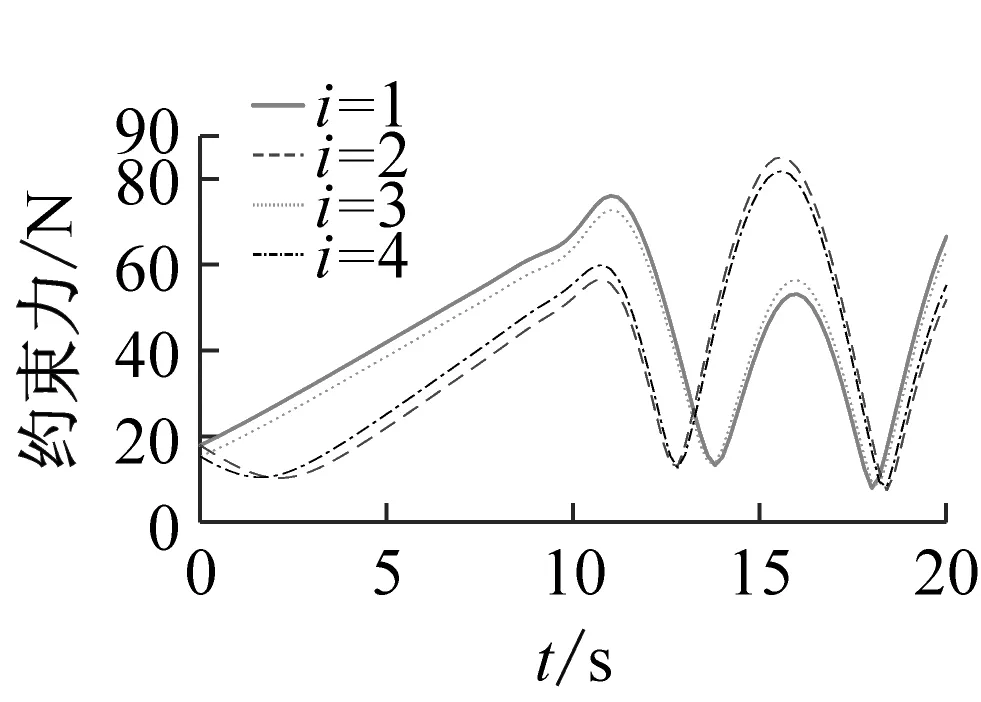
(d) 支鏈4圖17 球鉸副約束力Fig.17 Constraint force of spherical joints

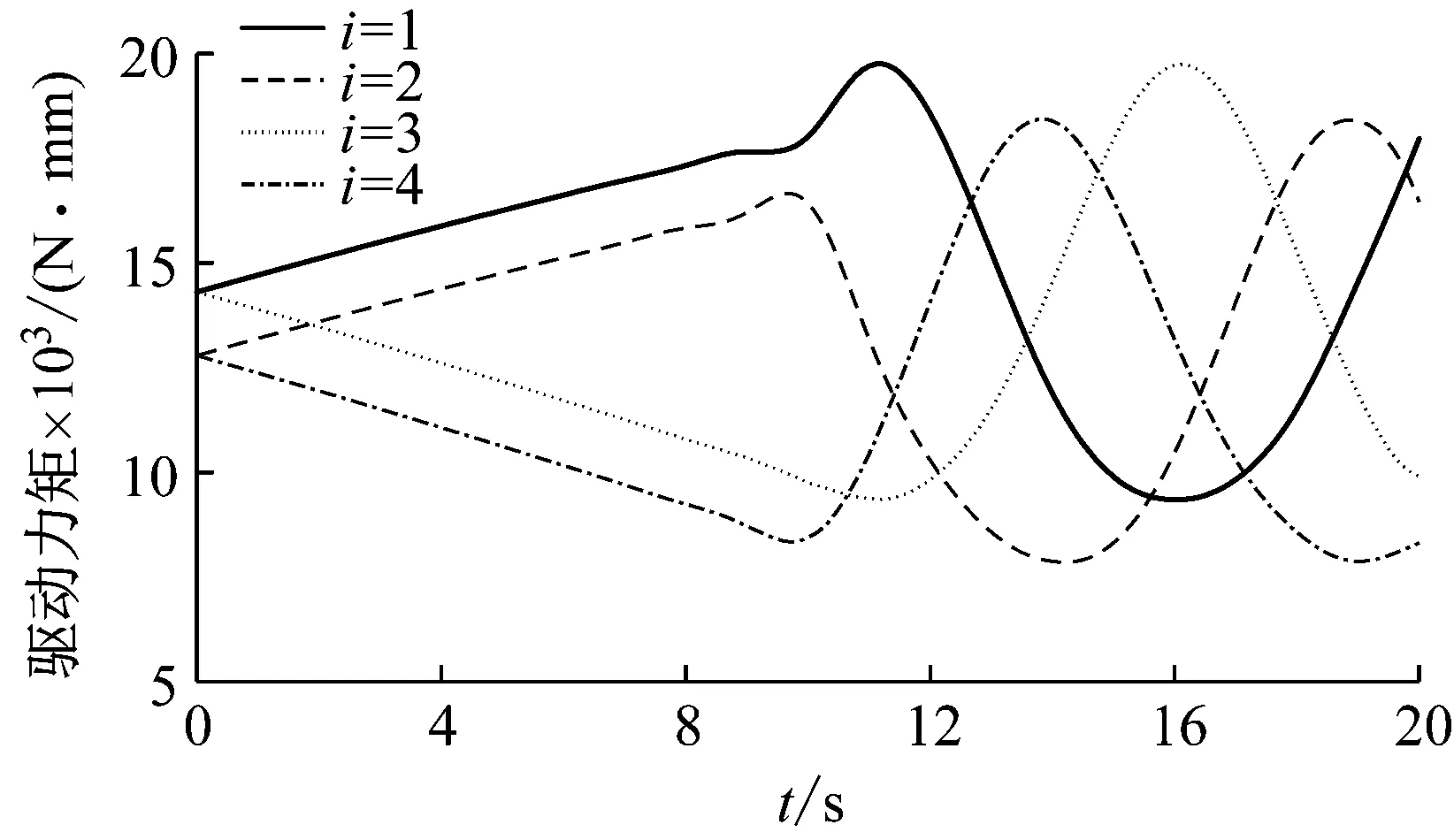
圖18 理論驅動力矩Fig.18 Driving torque of theory

圖19 理論值與仿真值誤差Fig.19 Error between theoretical and simulation value

3.2 20-sim仿真分析

在本節，將焊接機器人系統鍵合圖模型及其控制系統在20-sim軟件環境下進行仿真。其中伺服電機和減速器、熱風焊槍的一些基本參數如表2、表3所示。

表2 伺服電機及減速器的參數Tab.2 Parameters of servo motor and reducer

表3 熱風焊槍的參數Tab.3 Parameters of hot air welding gun

仿真計算時，可根據仿真基本參數和邊界條件，設置仿真積分算法和運行方式，將仿真結果以圖像顯示。使動平臺運行圖13所示軌跡，反解可得出電機電流的變化情況，如圖20所示。對比圖14和圖20可知，電機電流曲線和驅動力矩曲線的趨勢變化基本相同，驗證了HDPE膜焊接機器人系統的機、電耦合動力學模型的合理性。

圖20 電機電流變化Fig.20 Motor current variation

給定焊槍系統的輸入源并結合邊界條件，可對焊槍系統的多個參數進行觀測。本例選擇焊槍系統的熱力學溫度和質量作為研究對象，仿真結果如圖21和圖22所示。由圖21可知，溫度從環境溫度開始上升，并在達到穩定運行狀態時達到恒定值。假設動平臺行走速度恒定，控制系統輸入為運動學反解出的驅動關節角位移，熱系統輸出為質量流量。通過分析和仿真可發現，隨著時間增加，焊槍系統的焊料擠出量增多，質量變化曲線斜率不變，即熱系統輸出質量流量恒定，也就是單位時間內焊料擠出量不變，保證了焊道厚度一致。通過計算圖22中曲線斜率為0.833 g/s，與熱風擠出焊槍實際擠出量0.8 g/s非常接近，表明仿真計算具有較高精度。

圖21 焊槍內溫度變化Fig.21 Temperature changed in welding gun

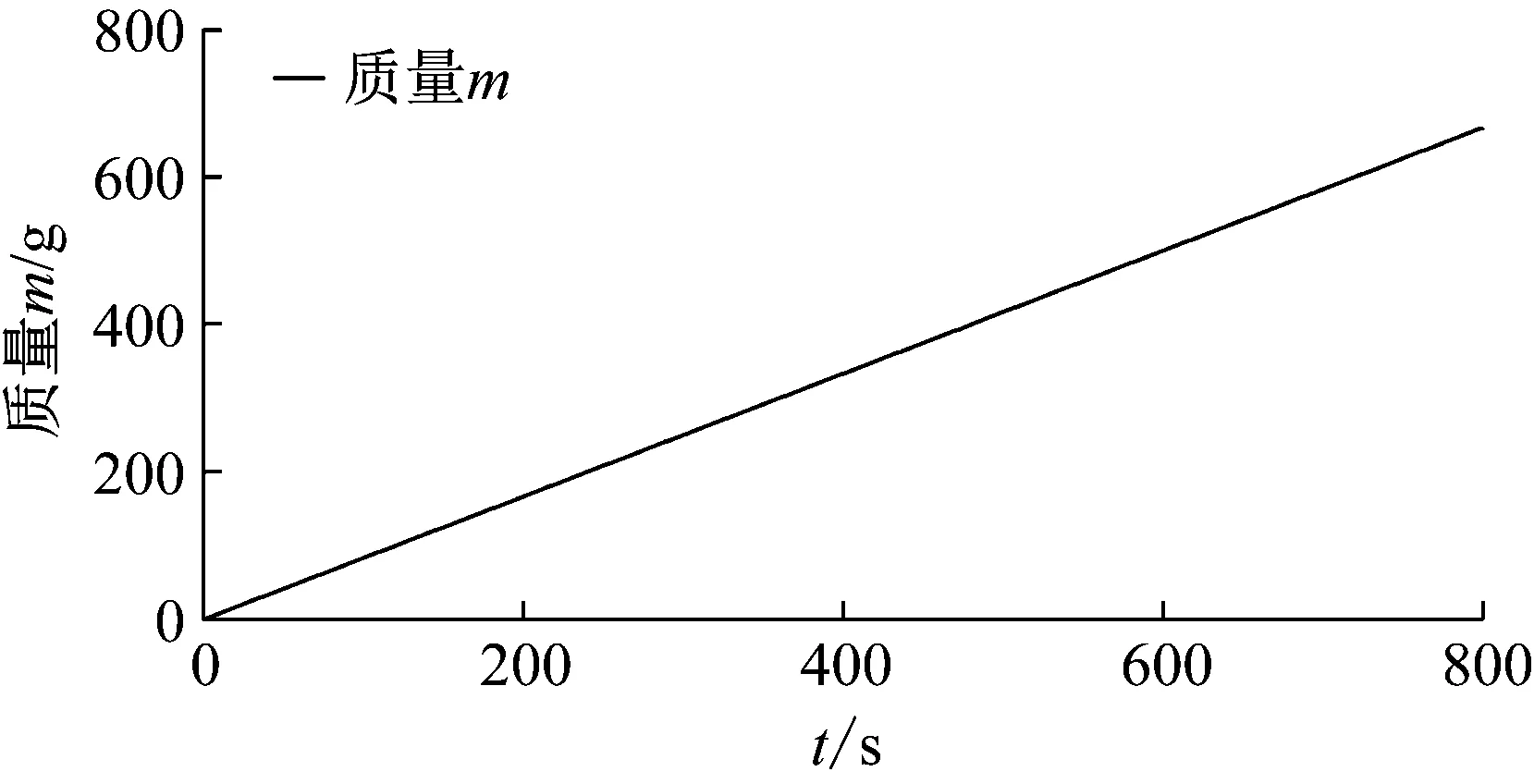
圖22 焊槍系統質量變化Fig.22 Quality changed in welding gun system

4 結 論

采用旋量鍵合圖及鍵合圖理論分別構建了填埋場防滲層智能修補并聯機構機械本體動力學模型及電機驅動子系統、末端熱熔焊執行子系統，考慮速度匹配，將旋量鍵合圖與熱系統鍵合圖相連，獲得機電熱耦合能域系統動力學全解模型，并通過MATLAB，ADAMS，20-sim仿真驗證了HDPE膜焊接機器人多能域系統動力學全解的合理性。