Coherent interaction and action–counteraction theory in small polaron systems,and ground state properties

Zhi-Hua Luo(羅質(zhì)華) and Chao-Fan Yu(余超凡)

School of Physics and Information Engineering,Guangdong University of Education,Guangzhou 510303,China

Based on the coherent interaction and action–counteraction principles, we investigate the ground state properties for small polaron systems, the coherent-squeezed fluctuation correction, and the anomalous lattice quantum fluctuation,with the new variational generator containing correlated squeezed-coherent coupling and quantum entanglement. Noting that -2t is the T.B.A. energy, for the coherent interaction effect, we find the ground-state energy E0 to be -2.428t, in which the coherent squeezed fluctuation correction -A0t is -0.463t (where t is the hopping integral, ω is the phonon frequency), with the electron–one-phonon coupling constant g=1 and the electron–two-phonon coupling constant g1 =-0.1. However, as a result of the action–counteraction effect, ?E0 is -2.788t, but -?A0t is -0.735t. As to the polaron binding energy (EP), for the coherent interaction effect, EP is -1.38ω, but for the action–counteraction effect, ?EP is-1.88ω. In particular, the electron–two-phonon interaction noticeably enlarges the coherent interaction and the coherent squeezed quantum fluctuation correction. By intervening with the quantum entanglement, the evolutions of the squeezed coherent state and the lattice quantum fluctuation begin to take control. At that time,we encounter a new quantum phase coherence phenomenon—the collapse and revival of inversion repeatedly for the coherent state in the entangled evolution.

Keywords: coherent interaction and action–counteraction, correlated representation variational approach,entangled-squeezed coherent state,interaction of electron with the coherent squeezed fluctuation

1. Introduction

The investigation of the properties of coupled electron–phonon (el–ph) systems and the related polaron behavior has played a central role in condensed matter physics for a long time. Because the coupling of electrons with the lattice vibration noticeably changes the characteristics of both electrons and phonons, it leads to a number of interesting effects and phenomena.[1–8]Over the last few years, effects due to the strong el–ph interaction and polaronic signatures have been evident in several compounds, such as hightemperature cuprate superconductors,[9,12]colossal magnetoresistance manganites,[8,11,13]fullerenes,[10]and DNA.[14]

This amount of experimental results has stimulated the study of different coupled el–ph systems. Among the most studied models, there is the Holstein lattice model[1,2](small polaron), and the Fr¨ohlich model (large polaron).[15,16]Recently, for the Fr¨ohlich polaron, the weak electron–phonon coupling region is fairly well described. For the arbitrary electron–phonon coupling strength, the variational approach,the variational path-integral,[22–24]the kernel polynomial,[25]and the polaron clusters method have investigated[18,19]further.

The Holstein model has motivated many studies since 1959.[1]The variational ansatz is expected to give reliable results only for ground-state properties.[26–28]In recent years,various methods,such as the variational path-integral,[25]density matrix renormalization group analysis,[29]and the exact diagonalization of small clusters,[30,31]have been used for studies of the Holstein model with special attention to the polaron problem. As we know,the local electron–phonon interaction leads to lattice localized distortion. For strongly coupled el–ph systems, the polaron is strongly localized, therefore the theory of strong-coupling el–ph systems has had some unsolved problems from the very time of its creation.[8,10,13]That is, the complex physics of the coupled el–ph systems in polar crystals and related polaronic behavior are far from a simple thing.[18,19,24,25]Recently, the variational wave function of a coherent two-phonon state for the lattice ground state was proposed by Zheng.[42]Feinberget al.[43,44]generalized this idea and showed how the squeezed state of the phonon is deeply related to the anomalous lattice fluctuation. At the same time, instead of the two-phonon coherent state expansion, we have proposed the variational approximation based on the squeezed coherent state expansion. In line with this new idea,for the arbitrary electron–phonon coupling strength,the ground-state energy of the Fr¨ohlich’s polaron systems is not only lower than the squeezed phonon state approach, but also goes beyond the results given by the Feynman path integral and the existing theoretical approximation.[22–24]Equally,for the system of Holstein’s polaron, the ground-state energy and the polaron binding energy also greatly exceed the results given by the two-phonon coherent state approach.[46]Furthermore, this new idea has generalized to the solution of quantum noise caused by the one-phonon coherent state field; for example,the persistent current in the mesoscopic ring and the quantum coherence dissipation in the quantum tunneling system with the spin–lattice phonon coupling.[47,48]

2. Coherent interaction theory, correlated representation variational method with quantum entanglement

2.1. One-phonon coherent state variational approximation,the nonlinear solitary wave

Taking into account the electron–two-phonon interaction,the Holstein’s Hamiltonian for coupled el–ph systems in onedimensional molecular crystals reads

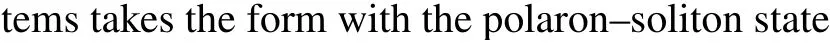
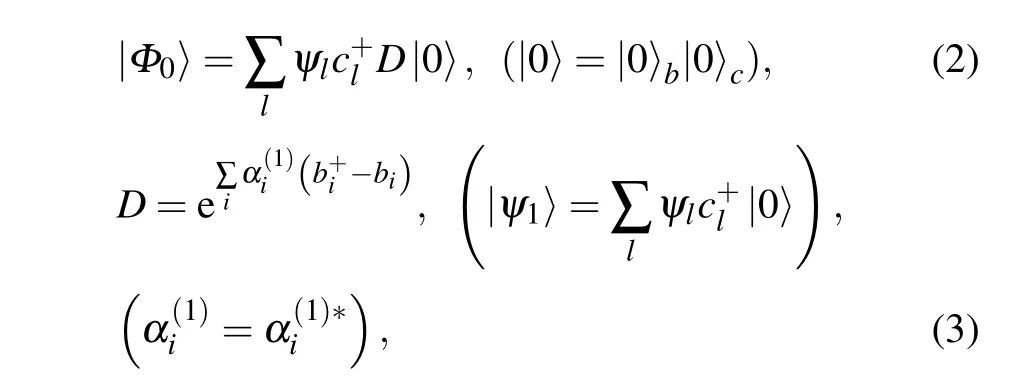
whereψidenotes the polaron–soliton state at the latticei,the variational parameters to be determined, and|0〉the vacuum state of the coupled el–ph systems.

In this manner, the ground state energy for the coupling systems will be given by

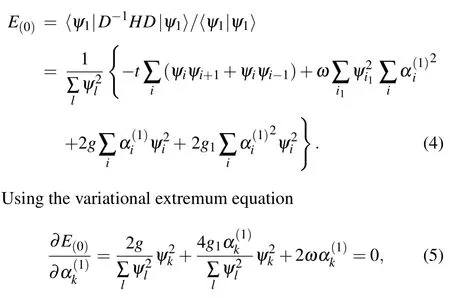
we can find for the nonlinear coherent parameteras

2.2. Correlated representation variational method based on the coherent interaction theory with quantum entanglement

3. Ground state based on the principles of coherent interaction and action–counteraction

3.1. Ground state based on the coherent interaction theory with quantum entanglement

Wheng1/= 0, noting that 2|g1|＜ω,ψ2＜1, and|A1|ψ2?1,as a reasonable non-linear expansion approximation to Eq.(24),the result is likely shown to be

3.2. Action–counteraction law correction

Fig.1. Variation of ground state energy ?E0 with the quantum entanglement versus the entangled parameter f1 at ω =1.0,t =1.0, g=1.0, g1 =-0.1,where ?E(1), ?E(2)0 stand for the electron–one/two-phonon interaction, respectively,E(0) shown in Ref.[38].

As is well known,considering the representation correlation betweenD(α)andS(z),the generator will be described by the joint generator with electron-displaced phonon correlation

4. Lattice phonon quantum fluctuation and binding energy of polaron based on the quantum entangled effect

In the light of the entangled state representation (9), we now investigate the new quantum entanglement behavior for the lattice quantum fluctuation and the binding energy of polarons in the polaron–soliton systems. Noting that

Noting that the electron–two-phonon interaction will enlarge the phonon squeeze action and will affect both the squeezed coherent state and the representation correlation,γwill develop to ?γ ?γ,α0η0to|?α0?η0|?|α0η0|,so〈Δ2?n〉=(f1+f2)2(?α0?η0)2ξ2〈Δ2n〉?〈Δ2n〉,thus〈Δ2?X〉?〈Δ2X〉,as shown in Figs.2 and 3.

Fig. 2. .Variation of lattice quantum fluctuation〈Δ2 ?X〉(unit ˉh/2Mω) versus entangled parameter f1 at ω =1.0,t =1.0, g=1.0, g1 =-0.1, where〈Δ2 ?X〉(1),〈Δ2 ?X〉(2) stand for the electron–one-phonon/two-phonon interaction,respectively.

Fig. 3. Variation of quantum fluctuation in between the phonon coordinate and the phonon momentum versus the entangled parameter f1 at ω =1.0,t=1.0,g=1.0,g1=-0.1,where〈Δ2 ?X〉〈Δ2 ?P〉(1),〈Δ2 ?X〉〈Δ2 ?P〉(2) stand for the electron-one/two-phonon interaction,respectively.

On the other hand, in terms of the coherent interaction betweenD(α)|0〉bandS(z)|0〉b, the binding energy of the polaron also leads to the important correction,

Fig.4. Variation of phonon–electron correlation parameter ξ(1)and ξ(2)versus f1 at ω =1.0,t=1.0,g=1.0,g1=-0.1,respectively.

Fig. 5. Polaron binding energy ?EP versus the entangled parameter f1 at ω=1.0,t=1.0,g=1.0,g1=-0.1,where ?E(1)P , ?E(2)P stand for the electronone/two-phonon interaction,respectively.

5. Summary,discussion and remarks

In synthesizing Section 1 and the results in Sections 2–4,some key physics and principal comments are obtained.

(i)Because of the coherent interaction betweenS(z)|0〉bandD(α)|0〉b, the coupled el–ph systems certainly evolve into the squeezed coherent stateS(z)D(α)|0〉bwith quantum entanglement but notD(α)S(z)|0〉b. The main quantum effects originate from the interaction of electrons with the coherent squeezed quantum fluctuation with quantum entanglement. As a result of the coherent interaction, the coherent

(iii) The local squeezed action and the non-local entangled action are not a result of their own action, but coexist with each other. That is, the local squeezed action parameterγ=f1f2and the non-local entangled action parameter(f1+f2) are interrelated withf21+f22=1. Because the local squeezed action and the non-local entangled action restrict each other’s evolution, the evolutions of the lattice quantum fluctuation and the coherent state cannot move forward to collapse and the stability of the ground state is assured. At that time, we will encounter a new phenomenon of the quantum phase coherence,in which the coherent state shows the revival of the collapsed inversion repeatedly.energy. By use of the polaron–soliton state wave function, the Debye–Waller coherent scattering effect is reduced fromte-(1/2)ξ2α(0)2≈0.375t(g=1.0,ω=1.0,ξ=1.4) tote-(1/2)ξ2?α(1)2e-4γ ≈t.

Acknowledgment

Project supported by the National Natural Science Foundation of China(Grant No.10574163).