Anisotropic plasmon dispersion and damping in multilayer 8-Pmmn borophene structures

Kejian Liu(劉可鑒) Jian Li(李健) Qing-Xu Li(李清旭) and Jia-Ji Zhu(朱家驥)

1School of Science,Chongqing University of Posts and Telecommunications,Chongqing 400065,China

2Institute for Advanced Sciences,Chongqing University of Posts and Telecommunications,Chongqing 400065,China

3Southwest Center for Theoretical Physics,Chongqing University,Chongqing 401331,China

We investigate the collective plasma oscillations theoretically in multilayer 8-Pmmn borophene structures,where the tilted Dirac electrons in spatially separated layers are coupled via the Coulomb interaction. We calculate the energy dispersions and Landau dampings of the multilayer plasmon excitations as a function of the total number of layers,the interlayer separation,and the different orientations. Like multilayer graphene,the plasmon spectrum in multilayer borophene consists of one in-phase optical mode and N-1 out-of-phase acoustical modes. We show that the plasmon modes possess kinks at the boundary of the interband single-particle continuum and the apparent anisotropic behavior. All the plasmon modes approach the same dispersion at a sufficiently large interlayer spacing in the short-wavelength limit. Especially along specific orientations,the optical mode could touch an energy maximum in the nondamping region,which shows non-monotonous behavior. Our work provides an understanding of the multilayer borophene plasmon and may pave the way for multilayer borophene-based plasmonic devices.

Keywords: plasmon,8-Pmmn borophene,multilayer,two-dimensional materials

1. Introduction

Graphene and the booming two-dimensional (2D) materials have been the superstars for their novel properties in condensed matter physics since 2004.[1]Now the 2D materials include not only graphene and the derivatives of graphene but also transition metal dichalcogenides (TMDs),[2–7]black phosphorus,[8–12]indium selenide,[13]stanene,[14–17]and many other layered materials.[18–23]Due to various advantages of the 2D materials, such as long lifetime,[24]gate tunability,[25,26]and optoelectronic applications,[2,27]they become promising materials for a wide range of nanophotonics and optoelectronics.[25,28–30]

Plasmon, the elementary excitation of the interacting electron/hole gas, with novel plasmonic phenomena like selective absorbance and scattering,subwavelength bound state,and local field enhancement, plays a fundamental role in researching the dielectric and optical properties of metals and semiconductors.[31]Resulting from the unusual linear dispersion of the Dirac massless electrons,graphene plasmons show the exceptional properties of electrical tunability, low intrinsic loss, and high optical field localization. In recent years,plenty of graphene-based plasmonic devices have been proposed theoretically and demonstrated experimentally, such as photodetectors,[32,33]terahertz lasers,[34]resonators,[35]and biosensors.[36–38]Along with graphene,plasmons in the other 2D materials, e.g., MoS2,[39]WTe2,[40]2H-TaSe2,[41]and phosphorene[42,43]also attracted more and more interests.

Several 2D boron structures have been predicted and experimentally fabricated.[44,45]As one of the most stable structures, the 8-Pmmnborophene, an orthorhombic lattice with three-mirror symmetry planes perpendicular to each other and a glide plane at one of the mirror symmetry planes,[46,47]belongs to the space groupPmmn(No.59 in Ref.[48]). The 8-Pmmnborophene reveals the tilted Dirac cone and anisotropic massless Dirac fermions by first-principles calculations,[49,50]which sharply contrasts the up-right Dirac cone and isotropic Dirac fermions in graphene. There have been reported that plasmon dispersion possesses the anisotropic behavior[51]and the tilt-induced kink[52,53]in 8-Pmmnborophene. However,the dependence on electron concentration of both the plasmonic resonance frequency and magnitude is relatively weak in monolayer 8-Pmmnborophene, limiting its applications in nanophotonics. One may expect the transparent photonic devices based on 8-Pmmnborophene/insulator stacks by depositing alternating wafer-scale borophene sheets and thin insulating layers, which could be grouped into photonic-crystal-like structures.

This paper presents a detailed study of the multilayer optical and acoustical dispersion in 8-Pmmnborophene. Within the quantum theory of the electron liquid, based on the matrix Dyson equation for the Coulomb propagator in multilayer borophene, we calculate the dispersion and Landau damping of plasmons and understand their dependence on the in-layer electron density,number of layers,and interlayer spacing.The plasmon spectra consist of one optical mode with a square-root dispersion andN-1 acoustical modes with linear dispersion.We show that the plasmon modes possess kinks at the boundary of the interband single-particle continuum, and the Landau damping drastically increases within the interband singleparticle continuum.All the plasmon modes approach the same dispersion at a sufficiently large interlayer spacing in the shortwavelength limit.The plasmons in multilayer borophene show the apparent anisotropic behavior,and the optical mode could touch an energy maximum in the nondamping region along specific orientations.

2. Model

The Hamiltonian of 8-Pmmnborophene is given by[54,55]

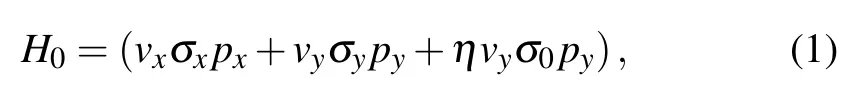
wherepx,yare the momentum operators,σx,yare 2×2 Pauli matrices, andσ0is a 2×2 identity matrix. The anisotropic velocities arevx=0.86×106m/s,vy=0.69×106m/s, andη=0.46 is the tilt parameter of Dirac cone.[54]The energy dispersion and corresponding wave functions of monolayer 8-Pmmnborophene are given by

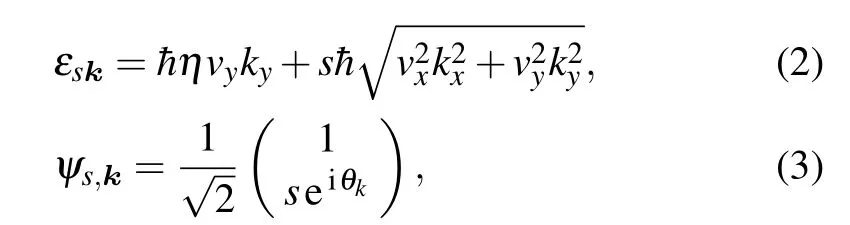
wheres=+(-) is the band index for conduction (valance)band andθkis the polar angle of the wave vectorkrespect tox-axis. Since the Dirac cone is tilted and the Fermi surface is not a circle but an ellipse, we define the Fermi vectorkFby letting the area of the elliptic Fermi surface the same as the area of a circle whose radius iskF. The Fermi energyεFcan be expressed by the effective Fermi vectorkFas[56]

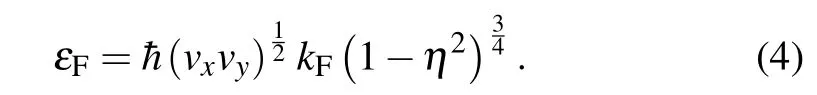
The tilted Dirac cone reduces to up-right Dirac cone(e.g.,the case of graphene)whenη=0 andvx=vy=vF.

We consider the structure of multilayer 8-Pmmnborophene with interlayer spacingdas shown in Fig. 1. The bare Coulomb interaction is a symmetric tensor

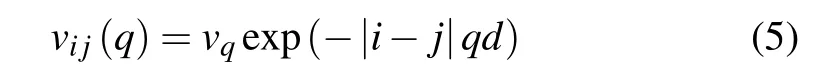
with respect to the layer indicesi=j=1, 2, ...,N. The off-diagonal(diagonal)elements represents the interlayer(intralayer) Coulomb interaction andvq= 2πe2/(κq) is the Fourier transform of intralayer Coulomb interaction withκbeing the static dielectric constant. Here we assume that the dielectric background of the environment surrounding borophene layers is homogeneous and can be well described by an average effective dielectric constant. Since the effective dielectric constant does not alter the dispersion of plasmon qualitatively,we can take the effective dielectric constant as 1,which merely means a renormalization of unit.[52]

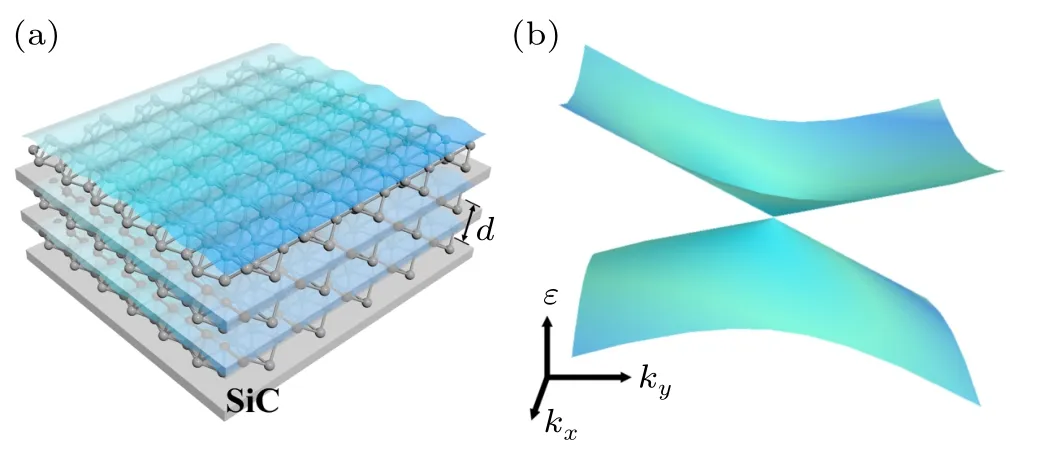
Fig. 1. Schematic diagram of plasmon for N-layer 8-Pmmn borophene.(b)The tilted and anisotropic Dirac cone in 8-Pmmn borophene.

Within a practical setup,the interlayer spacing ofdmultilayer 8-Pmmnborohpene should be sufficiently large so that the electron tunneling between layers is neglectable. Therefore, only the diagonal elements of the polarizability remains andΠ(q,ω)=δijΠi(q,ω).

The noninteracting Lindhard polarization function of each layer of 8-Pmmnborophene is given by

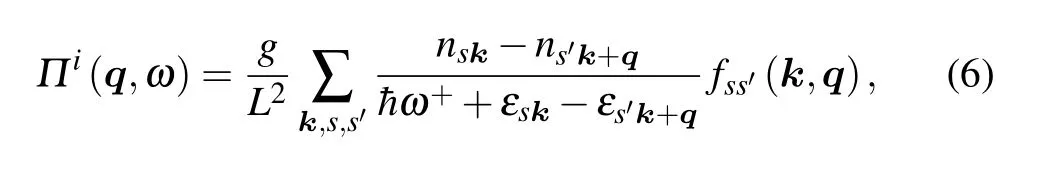
whereg=2 is the degeneracy from spin,nskrepresents Fermi function which reduces to step function in zero temperature andω+=ω+iδwithδ →0. From the wave functions of the 8-Pmmnborophene,the overlap function is given by

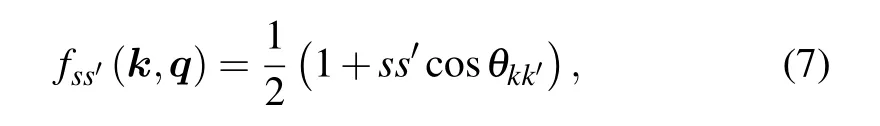
whereθkk′=θk-θk+q,θqandθk+qare the polar angle of wave vectorqandk+q,respectively.

The dynamical polarization function of monolayer borophene can be calculated by[52]

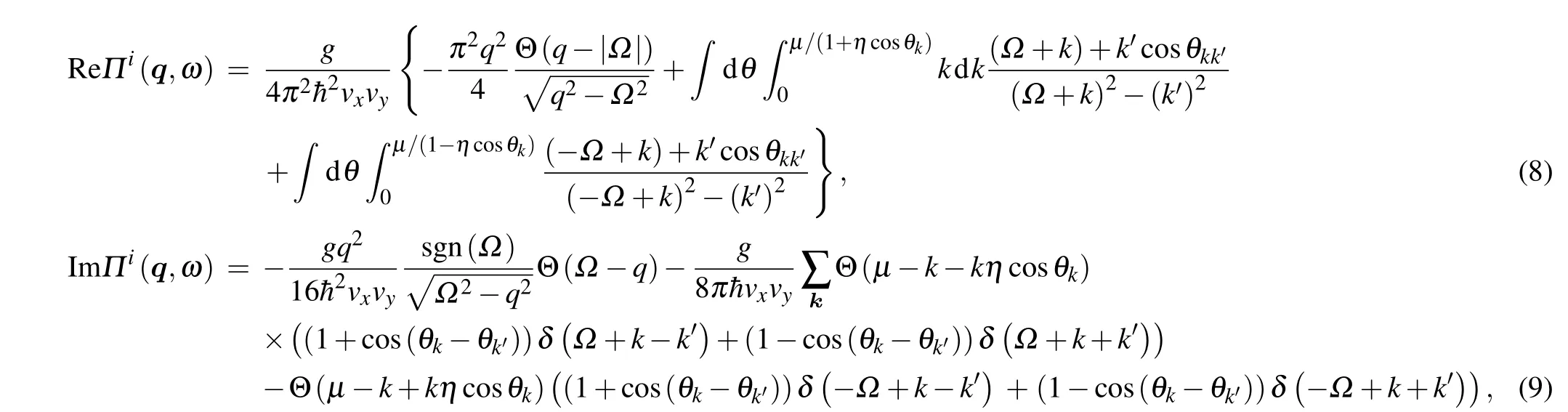
whereΩ=ˉhω-ˉhvxqηcosθq. Note that we have already assumed that the dielectric background is homogeneous. Then the plasmon dispersion can be calculated by the evaluating zeros of the dynamical dielectric functionε(q,ω),i.e.,

gives the damping of plasmons due to the properties of the intra/interband single-particle continuum.

3. Results and discussion

In the following paragraphs,we present our numerical results for the energy dispersion and Landau damping of multilayer 8-Pmmnborophene with the different number of layersN,interlayer separationdand polar angleθq. We calculate the energy spectrum from the general formula(10). In all figures,we adopt the unitsεFandkFfor plasmon energy and momentum,respectively. For the electron densityn=1012cm-2,we haveεF=106 meV andkF=2.507×106cm-1.

In Fig. 2, we plot the plasmon dispersion ofN-layer 8-Pmmnborophene withN= 2, 3, 4, and 5,d= 2 nm andθq=π/5.The plasmon dispersion in a monolayer is shown by a black dashed line for reference. There are two kinds of plasmon modes inN-layer 8-Pmmnborophene, one in-phase optical mode andN-1 out-of-phase acoustical modes. The inphase optical mode shifts to higher energies when the number of layers increases. With increasingN,the number of the multilayer acoustical modes increases correspondingly, and the energy of upper-lying modes enhances.In contrast,the lowestlying mode approaches the single-particle continuum boundary.The enhancement enables the top acoustical mode to cross the monolayer mode of five-layer borophene in the interband single-particle continuum. Notice that only two of the four acoustical modes are suppressed in five-layer compared with the acoustical mode in double-layer. In the short-wavelength limit,the behavior of multilayer plasmon modes shows a dramatic difference, which is in sharp contrast to graphene.[57]The optical mode has a kink at the boundary between the interband single-particle continuum and the nondamping region.However, the acoustical modes show rather faint evidence of the kink.

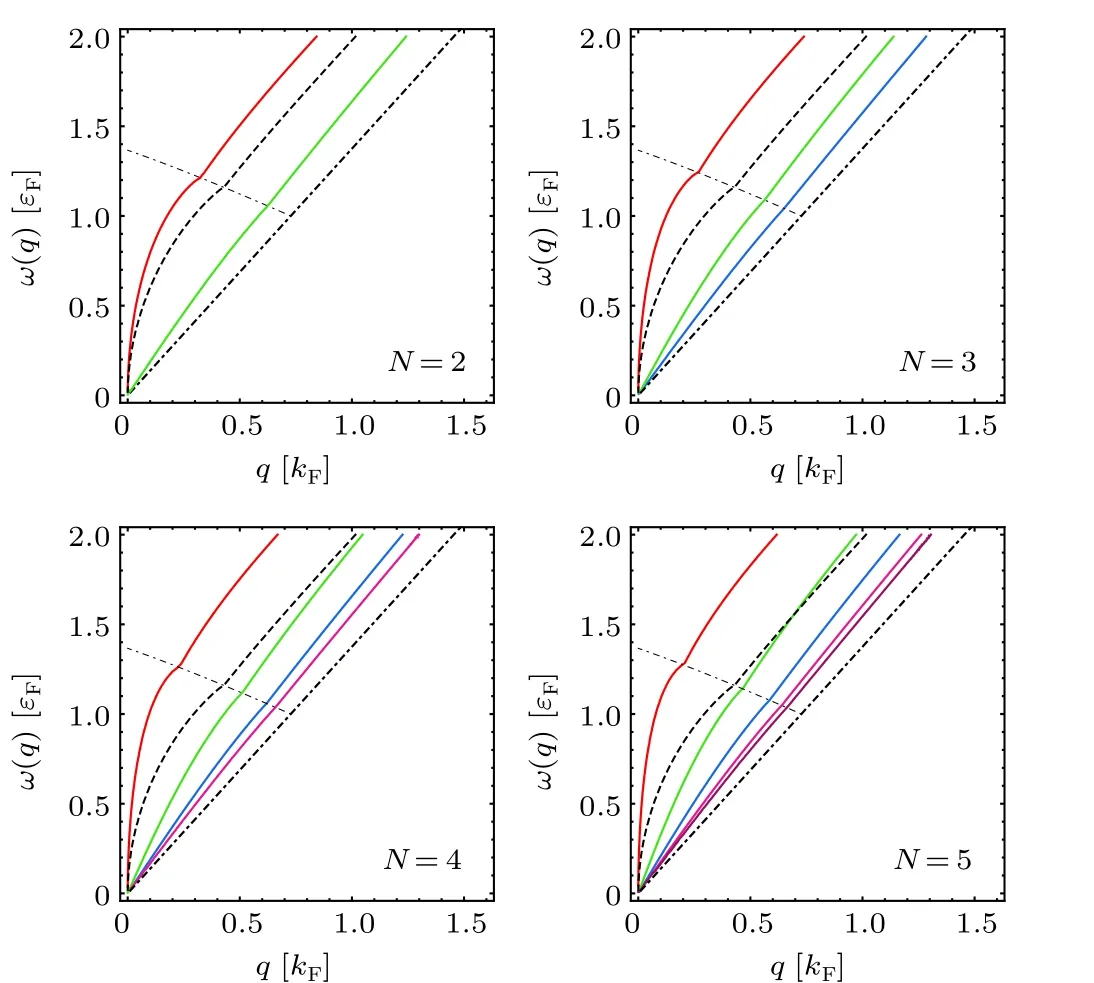
Fig.2. Plasmon dispersion for N-layer(N=2,3,4,5)8-Pmmn borophene with d = 2 nm, n = 1012 cm-2 and θq = π/5. The black dot-dashed line show the boundaries of intra-and inter-band single-particle continuum.Black dashed line is plasmon mode in monolayer 8-Pmmn borophene.Color solid line represent the plasmon modes.

In Fig. 3, we study the Landau damping of the corresponding multilayer plasmon modes shown in Fig.2. The energy enhancement for all multilayer modes results in a more extensive broadening of the corresponding plasmon dispersion, which dues to the increasing distance of the plasmon modes from the boundary of the intraband single-particle continuum. The Landau damping also shows the kink at the momentum corresponding to the boundary between the nondamping region and interband single-particle continuum,similar to the plasmon dispersion. The damping increases drastically in the interband single-particle continuum,which is in agreement with a previous study about the loss function of plasmons in monolayer borophene.[52]

In Fig. 4, we study the plasmon dispersion of threelayer borophene with various interlayer separationsd. The most apparent behavior is that the energy of in-phase optical mode decreases while the energies of out-of-phase acoustical modes increase with increasingd. However, all multilayer plasmon modes in the short-wavelength limit remain almost the same when the interlayer spacing is sufficiently large(e.g.,d= 10 nm), which reproduces the result in graphene multilayer.[57]This means all multilayer modes forq ?kFcoagulate around the monolayer plasmon mode independent of the number of layers if the interlayer separation is large enough. The physical reason lies in that the influence of the interlayer tunneling vanishes,and the plasmon branches from different layers behave independently. However, the kink of the optical mode is robust against the increasing interlayer separation. In contrast,the acoustical modes develop rather faint kinks on the boundary of the interband single-particle continuum.continuum is pushed down, and the energy of the plasmon modes decreases out of the long-wavelength limit. Asθqincreases from 0 toπ,the kinks become more and more apparent,especially for the acoustical modes. Note that the optical mode touches an energy maximum in the nondamping region,and the acoustical modes tend to behave like the optical mode when theθqapproachesπ. These anisotropic plasmons are caused by strong tilt Dirac dispersion of 8-Pmmnborophene.

Fig. 3. The damping function for N-layer (N = 2, 3, 4, 5) 8-Pmmn borophene with d =2 nm, n=1012 cm-2 and θq =π/5. Black dashed line shows the Landau damping function in monolayer 8-Pmmn borophene.Color solid line represents the Landau damping function.

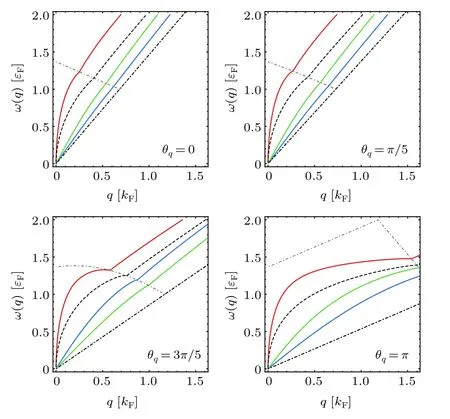
Fig. 5. Plasmon dispersion for three-layer 8-Pmmn borophene with n=1012 cm-2 and d=2 nm. (a)–(d)correspond to directions θq=nπ/5,with n=0,1,3,5. All other parameters and notations are the same as plasmon mode in Fig.2.

Fig. 4. Plasmon dispersion for threelayer 8-Pmmn borophene with n =1012 cm-2 and θq =π/5. Under the condition of d =2 nm, 3 nm, 5 nm,10 nm. All other parameters and notations are the same as plasmon mode in Fig.2.

Figure 5 shows the anisotropic spectra of the three-layer plasmon modes with different polar angleθq(θq=nπ/5,n=0, 1, 3, and 5). We can find that the plasmon modes possess different behavior in different directions. Compared with the case ofθq=0, the boundary of the intraband single-particle

4. Summary

In this paper, we have investigated the collective plasma oscillations theoretically in multilayer 8-Pmmnborophene structures,where anisotropic and tilted Dirac electrons in spatially separated layers are coupled via the Coulomb interaction. We calculated the energy dispersions and Landau dampings of the multilayer plasmon excitations as a function of the total number of layersN, the interlayer separationd, and the polar angleθq. The multilayer plasmon spectrum consists of one in-phase optical mode andN-1 out-of-phase acoustical modes. The energy of the in-phase branch and upper-lying out-of-phase branches of the multilayer plasmon increase with increasing the number of 8-Pmmnborophene layers,while the other branches decrease. The optical mode has an apparent kink at the boundary of the interband single-particle continuum, but the acoustical modes show rather faint evidence of their kinks. The Landau damping also shows a similar kink at the boundary and drastically increases within the interband single-particle continuum. As the interlayer separationdincreases, all the plasmon modes approach the same dispersion in the short-wavelength limit and sufficiently large interlayer spacing.We also show the anisotropic behavior of the plasmon in multilayer borophene. The optical in-phase mode touches an energy maximum in the nondamping region, and the linear dispersion of the acoustical out-of-phase modes becomes square-root dispersion when theθqapproachesπ. The presented numerical calculations provide an understanding of the multilayer borophene plasmon depending on the tunable parameters. Our work may pave a way for the plasmonic devices based on multilayer 8-Pmmnborophene.

Acknowledgments

This work was supported by the Scientific Research Program from Science and Technology Bureau of Chongqing City(Grant No.cstc2020jcyj-msxmX0684),the Science and Technology Research Program of Chongqing Municipal Education Commission (Grant No. KJQN202000639), and in part by the National Natural Science Foundation of China (Grant No.12147102).