基于多方向振動數據的風機齒輪箱故障智能診斷

孟繁曄，高翼飛，陳長征，2

（1.沈陽工業大學機械工程學院，沈陽 110870；2.遼寧省振動噪聲控制工程技術研究中心，沈陽 110870）

0 引言

齒輪箱作為風機中的重要部件，具有質量輕、體積小、傳動比大的優點，其運行狀態的好壞會對整體機械設備的穩定運轉產生影響。由于風機齒輪箱的工作環境大多是在高速度、重載荷、強沖擊的惡劣條件下，因此齒輪箱故障頻次較高。同時風能在國家中的能源占比正不斷攀升，所以對風機齒輪箱的故障診斷就顯得極為重要[1-3]。由于在復雜的工況下，強背景干擾成分的存在導致有效的故障特征信號難以被識別，所以進行故障診斷時首先需要對信號進行降噪處理，從而提高故障特征的比重，得到更優質的信號。近幾年隨著人工智能的不斷進步，使用數據驅動進行智能診斷正慢慢成為研究的熱門方法。原本傳統的診斷方法如快速傅里葉變換、小波變換等由于過度依賴專家經驗已慢慢淡出歷史舞臺，而在特征提取和識別方面有獨特優勢的深度學習已成為智能故障診斷中的“寵兒”[4-6]。

ESMD于2013年由王金良等提出，是著名的經驗模態分解方法（EMD）的新發展，相比于基礎的EMD，ESMD除了有自適應分解信號的特性，還可以通過極點對稱插值和自適應全局均線選取最優的篩選次數，從而能使模態混疊和端點效應有所緩解[7-8]。

MobileNet V2神經網絡是Google公司提出的主要應用在移動端設備的輕量化卷積神經網絡，在保證準確率的基礎上，大大降低了運算的時間及所需設備的要求[9-10]。

對于復雜工況下故障難以提取，同時降低運算所需設備的要求，并增加故障診斷的成功率，本文提出了一種結合ESMD、MobileNet V2及D-S證據理論的方法。該方法首先將3個方向原始的故障信號進行ESMD分解得到模態分量，利用相關系數進行信號重構，將3個方向重構后的信號輸入進MobileNet V2網絡中進行訓練，最后將得到的3個預測結果利用D-S證據理論進行融合計算并得到最終的預測結果。本文對代入某公司搭建的模擬實驗臺測得的數據集進行準確率的驗證，從而驗證方法的有效性。

1 基于ESMD的信號分解與重構

1.1 ESMD原理

ESMD流程如圖1所示，運算流程如下：

圖1 ESMD流程圖

1）找出原始信號或待分解樣本Y的全部極值點，包括極大值和極小值，并將其依次記為Ei（i=1，2，…，n）；

2）將相鄰的極值點Ei用線段相連，并將線段中點依次記為Fi（i=1，2，…，n－1）；

3）通過插值的方法將左右邊界的中點F0、Fn進行補充；

6）用原始信號與第一個經驗模的差值Y－M1重復上述步驟1）～步驟5），依次得到M2，M3，…，直到分解出殘余變量R，且R只剩符合要求的一定數量的極點。

ESMD分解放棄了原本的上、下外包絡插值曲線，選擇使用極值中點內部插值曲線，減少了異常極值點的波動影響；通過計算最佳模態分解次數，優化了分解的效果，對于解決模態混疊和端點效應問題都有了較大的進步。

1.2 信號重構

對信號進行模態分解，分解出數個IMF分量，并從中按照計算Spearman的相關系數的方法選出適當的IMF分量，進行信號重構。相比于原始的故障信號，重構之后的信號降低了高頻噪聲的成分比重，提高了信噪比。由于風機常處在惡劣的工況下，使用該方法能在一定程度上解決采集到的原始信號具有較強干擾的問題，雖然重構之后的信號仍然存在能量較高的噪聲干擾成分，但這一處理方法會對后面的神經網絡的自動提取有極大的幫助。

2 MobileNet V2模型

MobileNet V1網絡模型是在2017年由谷歌團隊提出并發表在2017年計算機視覺頂級會議CVPR上的輕量化網絡，由于大部分神經網絡是運行在計算能力較強的服務器中，而過于龐大的網絡無法在普通的電腦端或者移動端運行，針對這一問題，提出了該網絡。

MobileNet可以在保持模型精度的同時降低神經網絡參數的計算量。MobileNet V1網絡使用的是類似于VGG網絡的堆疊卷積操作，但區別是，前者將后者的標準卷積層轉變為深度可分離卷積。深度可分離卷積是2012年被提出、2013年被改進的。就是將一個普通卷積拆分為一個深度卷積和一個逐點卷積。深度卷積通過單通道卷積核，對每一個通道都進行卷積操作，同時并未改變輸出的深度，這樣操作過后得到的是與原通道數一致的輸出特征圖。但這樣可能會出現一個問題：由于通道數過少，特征圖的維度也過少，從而導致獲取到的有效信息可能會減少。接下來就引入了逐點卷積，逐點卷積就是1×1卷積，主要的作用就是進行升、降維操作。

深度可分離卷積可以使用更少的參數、更少的運算，達到計算相差不多的結果。

若使用3×3的卷積核，參數量和計算量均可以降為原來的1/8～1/9。同時，MobileNet采用了兩個全局超參數：width multipier（寬度乘法器）和resolution multipier（分辨率乘法器），這使得網絡在延遲度和精準度之間能進行有效地均衡，可以根據使用者對實際問題的大小選擇合適的模型大小。

除此之外，MobileNet V1網絡還將原本的ReLU激活函數換成了ReLU6激活函數。ReLU6函數的表達式為：ReLU（6）=min（max（0，x），6）。ReLU函數對大于0的值不進行任何處理，而ReLU6函數在輸入值大于6的時候，返回6，ReLU6“具有邊界性”，而其與原本的ReLU激活函數不同，作為非線性函數，ReLU6在低精度的計算下可能具有更強的魯棒性。

但是在實際使用中發現，深度卷積部分的卷積核比較容易出現訓練報廢的現象，即出現深度卷積訓練過后的卷積核為空的現象，所以在MobileNet V1的基礎上，改進提出了MobileNet V2網絡，結構如表1所示。其在本質上仍然屬于輕量化卷積神經網絡，架構是基于反向殘差結構。由于后者是前者的改進版本，所以后者仍然是采用深度可分離卷積實現特征的提取，因此MobileNet V2的參數量和計算量也大大減少。而兩者的區別主要有兩個方面：

表1 MobileNet V2網絡結構

1）MobileNet V2在深度卷積前增加一個1×1的“擴張層”，目的在于提升通道的數量，進而獲得更多的圖像特征。因為深度卷積自身無法將上層的通道數量進行增減，輸出通道數量取決于上層傳輸的通道數量。如果上層傳輸的通道數量過少，則深度卷積就處于低維狀態，進而無法獲取比較理想的特征，在深度卷積前加一個逐點卷積，可以使網絡在更高的維度提取特征。

2）MobileNet V2在最后一個激活函數上，舍棄了ReLU6激活函數，轉而使用了Linear激活函數。這是因為ReLU6在高維度中計算時保留的信息較多，丟失的信息較少，但在低維度中，卻反了過來，而最后是處于低維度中。為了避免出現卷積核信息為空的現象，MobileNet V2放棄了ReLU6激活函數，這樣可以保留更多的特征。

MobileNet V2與經典的網絡（如VGG16、GoogleNet）相比，無論是在計算的速度還是準確率上都更勝一籌，這是由于其網絡結構的特性；與當下流行的ResNet相比，在故障診斷率上與ResNet50相當，略遜于ResNet101，但是在計算的時間上，相較于前兩者都有明顯的進步，能很好地實現“輕量化”這一特點。

3 D-S證據理論

3.1 基本概念

1）識別框架。識別框架Ω定義為一共可以含有多少種假設，即表示的是需要判斷事件發生情況的范圍。

2）基本概率分配。基本概率分配簡稱BPA，指的是每一個研究方向對Ω全域中，每一種情況的基本概率的計算過程。

5）信任區間。在證據理論中，對于識別框架Ω中的某個假設A，通過計算Bel（A）和Pl（A），進而表示對某個假設的確認程度，如圖2所示。

圖2 信息的不確定性表示

3.2 Dempster合成法則

4 實驗驗證

4.1 實驗介紹

為驗證實驗結果，本文使用Inter Core i5-9400F CPU處理器、Windows10系統的計算機，使用Matlab2018a、Python3.7進行編程，并在Tensorflow2.0的框架下進行實驗。使用的是某公司搭建的風機齒輪箱實驗平臺，使用驗證的風機齒輪箱為天津某風場提供的齒輪箱，如圖3所示。

圖3 某公司風機齒輪箱實驗平臺

實驗一共分為2組，分別為軸承故障和齒輪故障。采集的方向包括水平、豎直、軸向3個方向，采用的是加速度傳感器。其中軸承故障為內圈故障、外圈故障和滾動體故障；齒輪故障包括點蝕故障、缺齒故障、齒根故障和齒表故障（如表2、表3）。同時每組實驗還對健康的狀態進行了檢測。由于實驗臺搭建在該公司的工作間中，周圍同時還進行著其他的工作與實驗，會帶來極大的噪聲干擾，這在一定程度上模擬了實際情況中風機齒輪箱惡劣工作環境帶來的干擾。

表2 齒輪箱軸承狀態

表3 齒輪箱齒輪狀態

4.2 實驗流程

由于采集信號過程中環境的嘈雜會帶來極大的噪聲干擾，故先將原始信號利用ESMD方法進行模態分解，隨后對IMF分量進行相關系數的計算，在各個狀態中，IMF1分量的相關系數均在0.9上下，即IMF1分量中包含絕大部分原始信號的特征，故將IMF1分量作為新的輸入信號。隨后使用Matlab2018a對新數據進行處理，由于數據樣本足夠多，為了保證數據的全面性，直接對每種故障類型的數據截成500段，每段截取信號長度為1024。雖然深度學習在計算機視覺等情況上發展得很好，但是碰到時間序列時，構建預測模型比較難，所以可將時間序列轉化成圖片，充分利用計算機視覺的優勢。故將1024個點按照32×32順序排列，隨后將其轉化為灰度圖，如圖4～圖5所示，即每種故障類型生成500個32×32的灰度圖作為輸入的數據。

圖4 軸承4種故障水平方向對應灰度圖示例

圖5 齒輪5種故障水平方向對應灰度圖示例

將每種狀態中的450張作為訓練集，50張作為測試集。故軸承訓練集一共包含了4種狀態，1800張圖片，測試集包含200張圖片；齒輪訓練集一共包含5種狀態，2250張圖片，測試集包含250張圖片。將每個方向上的數據輸入到MobileNet V2神經網絡中進行訓練，epochs取200，一共訓練10次，取平均值，隨后將輸出的結果利用D-S證據理論進行融合計算后得到最終的故障診斷準確率，實驗流程如圖6所示。

圖6 實驗流程圖

4.3 實驗結論

4.3.1 軸承對比實驗

一共訓練10次，取均值，將結果圓整后，得到混淆矩陣如圖7所示。

圖7 3方向軸承故障診斷圓整后的混淆矩陣圖

故障診斷的準確率分別為：水平方向為67%，豎直方向為75.5%，軸向為56.5%。隨后將輸出的結果利用D-S證據理論進行融合，計算后得故障診斷準確率為83.31%。為了做對比，將原始的無ESMD處理的信號輸入到網絡中訓練10次，取平均數并對其進行相同的數據融合操作，得各情況準確率如表4所示。

表4 各情況準確率表%

通過對比可知，第一種情況，在不進行ESMD分解和沒有D-S理論證據的數據融合時，取3個方向的最高值，準確率僅僅能達到73.2%，這與工作環境的嘈雜和使用的加速度傳感器位置的偏差及加速度傳感器本身的精準度有關，但這極大可能地模擬了實際環境中的風機齒輪箱診斷的情況。而在第二種情況中，使用ESMD分解，但不使用D-S融合理論，即取單方向最高診斷準確率，可以達到75.5%，相比于第一種情況，提升了大約1%～2%，這證明了ESMD分解及隨后信號重構的效果，能達到降低噪聲的作用，進而使故障特征更明顯，從而提高神經網絡的診斷準確率。第三種情況，在不使用ESMD的條件下，使用D-S證據理論進行數據融合，3個方向的診斷結果相互作用、互相印證，使得故障診斷準確率相比于前兩種情況都有大幅的提升。第四種情況，也是本文所使用的方法，由于在每個方向上均使用了ESMD分解及信號重構方法，使得單方向上的故障診斷準確率得以提升，隨后再依據D-S證據理論進行數據融合，進而達到83.31%的準確率，相比于前3種情況，均有較大的提升。

隨后使用其他網絡進行了同樣的操作，計算時間及準確率對比如圖8所示。

圖8 網絡的計算時間及準確率對比圖

由此可見，本文選用的方法在保證一定準確率的同時，可以大大減少計算的時間，減輕對設備的要求。

4.3.2 齒輪對比實驗

同軸承相似，利用取均值并圓整后的混淆矩陣計算得到3個方向齒輪故障診斷圓整后的混淆矩陣圖如圖9所示。

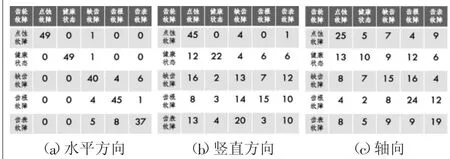
圖9 3 個方向齒輪故障診斷圓整后的混淆矩陣圖

齒輪的故障診斷準確率分別為：水平方向為88%，豎直方向為42%，軸向為37.2%。通過3個方向的故障診斷比較，發現豎直方向和軸向的故障診斷準確率遠低于水平方向，這可能與當時測量的環境與加速度傳感器的優劣度有關，但分析其輸出的混淆矩陣可以得知，并無明顯的證據證明存在沖突現象，故可以使用D-S證據理論對數據進行融合，融合后的結果為94.78%。有此結果可知，在故障診斷中，獲得多個方向的故障診斷數據，即便有幾個方向準確率較低，但在無明顯的信息沖突情況下，融合后依然高于單方向的診斷準確率，這也證明了本文使用方法的有效性。

5 結語

針對風機齒輪箱故障診斷問題，本文提出了一種結合ESMD、MobileNet V2及D-S證據理論的方法，并運用實際搭建的風機齒輪箱實驗平臺獲得的數據集進行實驗驗證，同時設置了對照實驗，分別與使用不同的網絡和不使用ESMD及D-S證據理論進行對比。實驗結果表明，在保證準確率的情況下，本文提出的方法大大提高了運算的速度，實現了輕量化。未來工作將進一步提升診斷的準確率并實現移動端或嵌入式設備的診斷。