考慮關鍵件加工質量的雙資源約束車間調度算法

孫愛紅 宋豫川 楊云帆 雷 琦

重慶大學機械傳動國家重點實驗室，重慶，400044

0 引言

產品質量的形成過程中，某些關鍵件的加工質量是影響產品質量的重要因素，制造商在保證盈利水平的條件下，必須尋求切實可行的生產策略以盡可能地提高產品質量。

近年來，資源約束型作業車間調度問題逐漸受到國內外學者的廣泛關注。MONDHER等[1]從研究方法、機床柔性、工人柔性、優化指標、求解方法、方法框架等6個方面，對雙資源約束作業車間調度問題(dual-resource constrained job shop scheduling problem，DRCJSP)和雙資源約束柔性作業車間調度問題(dual-resource constrained flexible job shop scheduling problem，DRCFJSP)的部分工作進行了回顧，其中涉及到的優化目標有利潤、完工時間[2]、工人數、延遲訂單數、生產成本、生產效率、拖期[3]、能耗[4]、噪聲污染、工人調動次數等。WU等[5]針對DRCFJSP建立了以最小化最大完工時間和準結時間為目標的數學模型。孔繁森等[6]為獲得人機聯合任務分配問題的最優資源利用方案，建立了以資源利用均衡率、工人任務復雜度均衡率、平均認知度為約束條件，以最小化平衡滯延時間為目標的人機聯合任務分配模型。以上研究考慮的目標多涉及資源(時間、人力、物力、財力、環境等)的有效利用，幾乎沒有考慮產品的加工質量，可能導致相關目標完成而加工質量難以保障的問題，并且此類問題在資源有限的場景中更容易出現。

有研究從以下兩個方向來保障產品質量。一是從整體的角度出發，以提高總體工件加工質量為目標來保障產品質量[7-9]，這要求所有工件同等重要，工件之間不存在優先等級。通常來說，不同工件的重要程度必然不同，因此，以整體加工質量為優化目標可能造成部分非關鍵件搶占關鍵件的優秀資源，導致非關鍵件加工質量過剩，而關鍵件質量未達到預定加工要求。二是從關鍵件/關鍵工序出發，對加工要求高的關鍵件或關鍵工序指定特定的工人/機床來加工，以保障其加工質量[10-11]，這雖然在一定程度上滿足了關鍵件的加工質量要求，但資源柔性降低，導致某些特定工人/機床的工作量過大，調度目標優化程度下降。

因此，為進一步完善產品加工質量的保障策略，本文結合生產車間的實際情況，考慮關鍵件加工質量、準備時間、機床類型、人和機床加工異質性等因素，建立了雙資源約束柔性作業車間調度問題模型，將關鍵件加工質量閾值作為約束條件，在保障關鍵件加工質量的同時提高總體工件的加工質量，并以最小化最大完工時間為目標，設計了基于時窗的活動調度策略的兩級嵌套蟻群算法進行求解，在實現優化調度目標的過程中，不斷提高關鍵件和整體工件的加工質量。

1 問題描述和數學模型

1.1 問題描述

考慮關鍵件加工質量的雙資源約束柔性作業車間調度問題可以描述為：w個工人操縱m臺機床加工n個工件，工件中有nc個為關鍵件，各工件包含多道工序且每道工序有多臺可選加工機床，同一工序在不同機床上的加工時間可能不同。車間內部的機床可分為普通機床和數控機床。對于數控機床，工人僅需負責工件的上下料、清洗等準備工作，而普通機床工人則需參與準備工作以及工件加工的全過程。若工件在某一機器上連續加工，則工人只需對連續工序的首道工序進行相應的準備工作。工人數目小于機床數目，每個工人具備操作一臺以上機床的能力，工人操作不同機床的加工合格率以及不同機床的加工合格率不一定相同。關鍵件的加工質量(由工件各道工序的工人和機床的加工合格率來體現)需在加工質量閾值上。調度任務為每一道工序安排合適的機床、工人和順序，在滿足關鍵件加工質量要求的前提下，使得工件的總完工時間最小、整體加工質量水平更高。

為簡化問題，本文給出如下假設：①各工件的每道工序在不同機床上的加工時間已知；②同一時刻一臺機床只能加工一個零件；③每個工件在某一時刻只能在一臺機床上進行加工，不能中斷；④不同工件的工序之間沒有先后順序約束；⑤不同工件之間具有相同的加工優先級；⑥工人可以操作的機床集合已知；⑦每個工人在任意時刻只能操作一臺機床；⑧在零時刻，所有工件均可被加工；⑨不同機床、工人的加工合格率是已知的。

1.2 數學模型

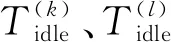
基于以上定義，給出調度目標函數：

min(f1)=min(maxCk)

(1)

(2)

(3)

(4)

式中，f1為總完工時間；f2為總加工質量水平。

(5)

TRijkl=Tijk(1-Hk)(2-elk)+TijkHk

(6)

(7)

(8)

STi(j+1)qr≥ETijkl

(9)

(10)

YijklYxyqr(ETijkl-STxyqr)(STijkl-ETxyqr)≥0

(11)

YijklYxykr(ETijkl-STxykr)(STijkl-ETxykr)≥0

(12)

(13)

(14)

STijkl≥0

(15)

式(5)表示關鍵件的加工質量需滿足給定質量要求；式(6)、式(7)分別表示機床和工人的實際加工時間；式(8)說明工序實際加工時間取決于機床、工人的選擇以及工序加工的排序情況；式(9)反映了工藝加工順序，每個任務必須按工序的先后順序完成；式(10)表示每道工序只能由單個工人操作一臺設備完成；式(11)表示每臺設備在任意時刻只能完成一道工序；式(12)表示每個工人任意時刻只能操作一臺機床；式(13)、式(14)分別表示設備為普通機床和數控機床時的工序可選完成時間；式(15)表示所有工序的開始加工時間都大于零。

本文考慮的是完工時間f1和質量f2的多目標優化問題。企業主要關注生產性能時，會更看重f1，而輕視f2。為處理這種情況，將f1設定為主要優化目標，將f2看做附帶優化目標。如果同等對待兩個目標，則企業會忽略那些f2偏高的解，因為那些解不符合他們的偏好；相反，將附帶優化目標嵌入到優化過程中，附帶優化目標也能得到充分優化。

2 算法設計

蟻群算法因原理簡單、通用性好、條件約束少等特點而被廣泛用于求解組合優化問題。針對考慮了關鍵件加工質量的DRCFJSP，本文設計了一種兩級嵌套蟻群算法來進行求解，算法的第一級為工序排序層，第二級為資源指派層。此外，根據問題的特點，設計了一種新型候選集來保證解的可行性，并提出了一種基于時窗的活動解碼來提高解的質量。螞蟻尋優過程可視為以最小化總完工時間為主要目標的單目標尋優，使主要優化目標充分優化，附帶優化目標通過保質策略在尋優過程中不斷優化。

2.1 候選集設計

螞蟻在尋跡之前，要預先設置候選集D、禁忌集T。候選集D中存放螞蟻下一步可選的節點，即螞蟻的可選路徑集；禁忌集T中存放螞蟻已經過的節點，不允許再次選擇。合適的候選集設計可以保證生成解的可行性以及尋優效率。劉曉陽等[12]為保障裝配序列可行，根據干涉矩陣，以裝配域為單位進行干涉檢查，將具有可裝配性的裝配單元組成了候選集。黃學文等[13]用蟻群算法求解基于OR子圖(or-subgraph)描述的多加工路徑柔性作業車間調度問題時，結合OR子圖的Allowed列表生成算法(簡稱ORA算法)生成候選集。以上文獻設計的候選集未考慮螞蟻路徑的壓縮，只要螞蟻到達到這個節點，下一步的所有可選節點都加入候選集。張潔等[14]研究了螞蟻路徑的壓縮策略，針對螞蟻可選路徑在搜索過程中移動范圍固定、不利于保持群體多樣性等缺點，提出一種通過衡量螞蟻節點加權散度來確定候選集大小、進而提高搜索效率的路徑壓縮方法。本文設計了兩種候選集：可選加工工序候選集、工序對應的資源組合候選集。對于資源組合候選集，如果工序對應工件是關鍵件，則應保證當前所選資源組合不會導致目前及以后的加工質量低于閾值。

2.1.1工序候選集

工序選擇的螞蟻地圖是(N+1)×N(N為總工序數)節點的網絡。由于工藝約束限制，每個工件在任意時刻至多有一道工序等待加工，因此每只螞蟻的實際可轉移個數不多于工件數n。候選集確定為n個工件未加工工序的第一道工序。例如，若有5個待加工工件，它們的總工序數分別為3、4、4、3、4，已加工工序數分別為1、1、4、3、1，則工序候選集S={O12，O22，O44，O52}。

2.1.2資源組合候選集

資源組合選擇的螞蟻地圖由總工序數N和總資源組合數Npair組成的N×Npair網絡構成。對于給定的工序Oij，首先確定可完成Oij的工人、機床組合；接著判斷該工件是否為關鍵件。若為非關鍵件，則所有工人、機床組合即為候選集；否則，需確保關鍵件滿足閾值條件。資源候選集的確定步驟如下：

(1)找出加工該工件每道工序的最好資源組合Mijb和Wijb，得到該工件i可達到的最好加工質量：

(16)

式中，ρMijb為機器Mijb的加工合格率；ρWijbMijb為工人Wijb操作機器Mijb的加工合格率。

(2)記初始加工質量Qi=1。根據已完成工序所選的資源組合確定當前工件能達到的最好加工質量Qibn，找出加工該工序的全部資源組合B，由Qi和Qib得出全部資源組合中能使工件的加工質量得以保證的加工該道工序的資源組合：

(17)

(18)

(3)確定該工序的加工資源[k，l]后，更新Qi：

Qi←Qiρkρlk

(19)

2.2 基于時窗的活動調度策略

調度策略的不同決定了調度結果的好壞。為此，MENG等[15]針對考慮能耗的DRCFJSP，給出了半主動解碼、主動解碼、貪婪解碼和考慮能耗解碼的4種調度策略。李兢堯等[16-17]對時窗、時窗操作做了詳細介紹，針對復雜制造環境下DRCFJSP的機床時窗與工人時窗的不同，提出了時間比較策略，為每道工序快速選擇滿足其工藝約束的最早調度時窗。除半主動解碼方法外，上述調度策略均可總結為：當前工序的開工時間為所選資源約束下第一個可用時窗的最早開始時間或該工序前序工序的完工時間。實際調度中，雖然這種貪婪的思想能充分利用空閑時間，但所有的工序的調度都取可用時窗的最早可加工時間不一定會得到滿意的調度結果。圖1中，實線方框表示已加工工序，虛線方框表示待調度工序，虛箭線箭頭所指為調度結果工序，方框中的“2-1”表示工件2的第一道工序。圖1a、圖1b給出了在機床M1上使用基于貪婪思想的主動調度下的工序“2-2”和“4-1”的調度過程。時間窗[2，5]是工序“2-2”的第一個可插入的時間窗，其中，工序“2-2”于時間窗[2，5]的最早可開始時間2開始后，工序“4-1”不能再次插入時間窗[2，5]。為彌補基于貪婪思想方法的缺陷，本文改進了貪婪思想的解碼方式，提出一種基于時窗的活動調度策略。這兩種策略的差異體現在工序的開始時間是否為最早可用時窗的最早可開工時間。圖1c、圖1d所示的調度過程中，工序“2-2”的完工時間與第一個可用時間窗[2，5]的后序工序的開始時間相同，但開始時間不再是該工序在時間窗上的最早可開始時間，于是工序“4-1”在調度時可插入該時間窗，使得調度結果比前者更優。

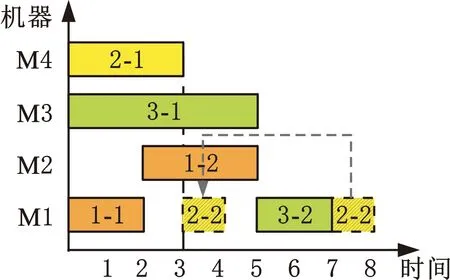
(a)工序插入時窗的最早可開始時間調度圖

若第一個可用時窗的開始時間WST晚于其前序工序的完工時間ETOi(j-1)，則該工序的開始時間STOij為WST。若第一個可用時窗i的開始時間WST早于其前序工序完工時間ETOi(j-1)，則需判斷其前序工序的完工時間是否為該工序的開始時間。于是，該工序的開始時間為

STOij=

(20)

(21)

其中，LenWi為時間窗i的時窗長度；AveTk為所有可在機床k上加工的全部工序的平均完成時間；Kijk表示工序Oij是否能在機床k上加工，若是，Kijk=1，否則，Kijk=0。

于是，在基于時窗的活動調度策略上，考慮人員柔性、設備屬性，設計了一種基于時窗的活動調度策略的DRCFJSP調度策略，時窗可分為工人加工時窗(工人參與加工的連續時間段)/空閑時窗(工人空閑的連續時間段)和機床加工時窗(機床加工的連續時間段)/空閑時窗(機床空閑的連續時間段)，如圖2所示，可以看出加工時間的確定需要使用2種規則。

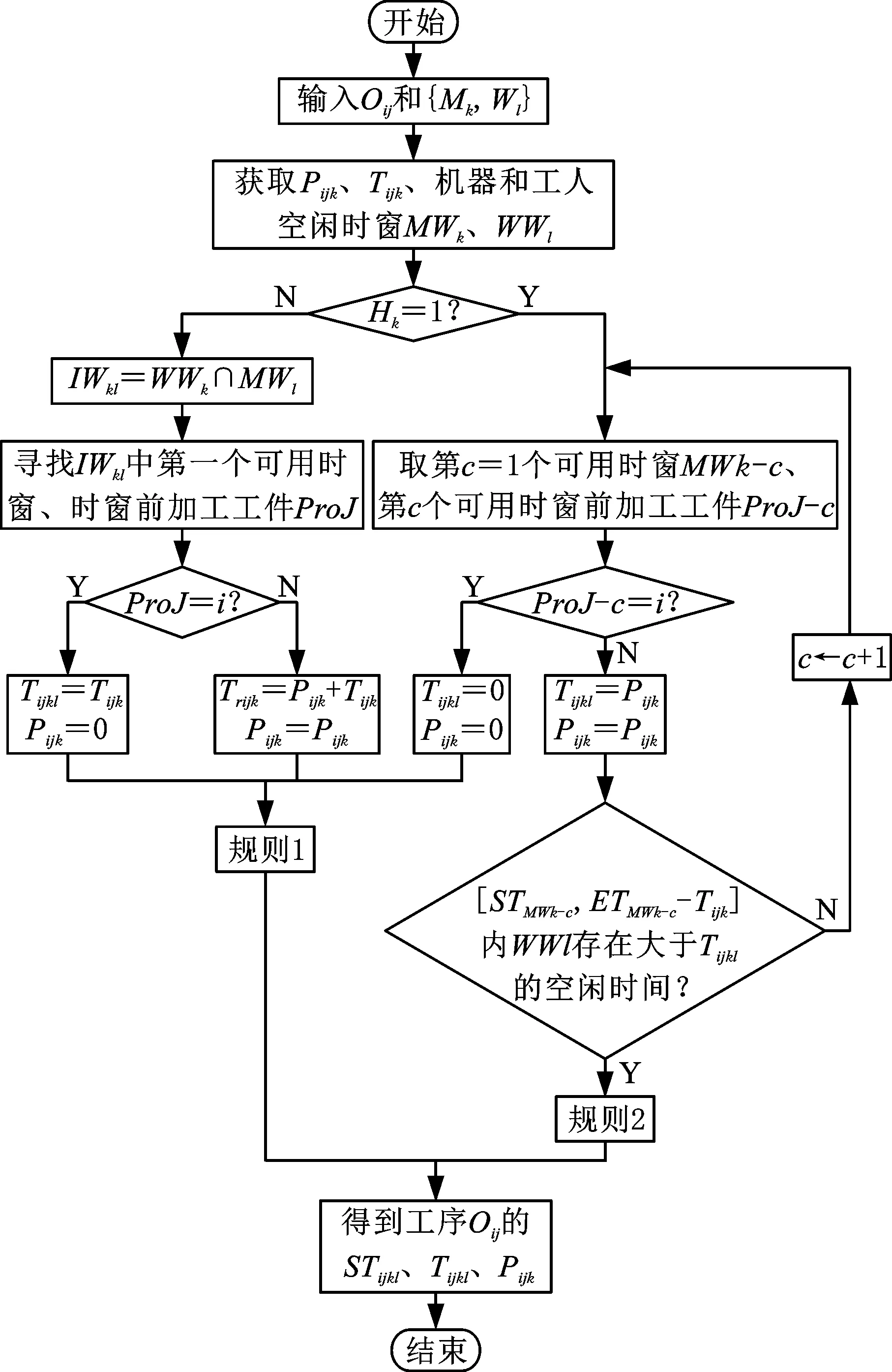
圖2 考慮人員柔性和機床類型的DRCFJSP調度流程圖

規則1當所選機床為普通機床或工人加工時間為零時，工序Oij的開工時間與Oi(j-1)結束時間、工人或機床可用空閑時窗的形式開工時間、完工時間有關，工序Oij的開始時間STijkl=min(STi(j-1)，Tws，Tms)，其中，Tws、Tms分別為工人l和機器k的可用時窗的開始時間。

規則2當所選機床為數控機床且工人加工時間不為零時，工序Oij的開工時間不僅與Oi(j-1)的結束時間及機床可用時窗的開始結束時間有關，還與工人的時窗有關，如圖3所示。圖3描述了所選機床為數控機床、機床空閑時窗可用的情況下，工人空閑時窗也可用的4種情況，圖中符號Tws、Twe分別為工人l的可用時窗的開始時間和結束時間；Tms、Tme分別為機器k的可用時窗開始時間和結束時間，Tle為工序Oij的前序工序的完成時間。工序Oij的開始時間為

(a)情況1

STijkl=

(22)

(23)

式中，Tp為工人l加工時間的最晚結束時間。

2.3 考慮關鍵件加工質量的保質策略

有別于將加工質量當作多目標中的一個指標進行優化和指定特定工人和機床處理關鍵件/關鍵工序的方法，本文提出的策略是將加工質量f2看作附帶優化目標，即在關鍵件加工質量得到保證的前提下，不斷提高關鍵件加工合格率閾值和總體加工質量水平閾值。目標f2的優化策略的具體步驟如下：

(1)記螞蟻總數為Anum，初始滿足關鍵件加工合格率閾值的完工時間為C0、總體加工質量水平為Q0。對所有解的加工質量水平f2降序排序，若排在第μAnum位的f2μ>Q0，則更新Q0；否則，Q0不變，其中，μ的取值通常為0.1～0.2。

(2)在每次迭代過程中，將不滿足總體質量閾值條件的解淘汰。

(3)判斷排在第μAnum位調度解的關鍵件加工合格率和完工時間f1μ，若f1μ>C0且關鍵件的加工合格率大于關鍵件質量加工合格率閾值，則更新Q0和C0。

(4)以f1為目標不斷進行優化迭代直至達到終止條件。

對于關鍵件加工質量閾值，由于生成解的過程保證了可行解始終滿足關鍵件的加工質量閾值條件，所以本文的保質策略無需考慮每個調度解各關鍵件是否滿足閾值條件。隨著總體加工質量水平閾值的不斷提高，最終解的加工質量將處于一個比較高的水平。

2.4 局部搜索

蟻群算法通過信息素和啟發式信息引導螞蟻從候選表中選擇作業，對于本文設計的兩級嵌套蟻群算法，螞蟻要經過工序選擇和資源選擇兩個階段的狀態轉移過程。偽隨機比例狀態轉移規則既可以避免陷入局部極小值，又可避免因隨機造成的概率性劣向轉移，常能取得較好的全局優化性能。工序選擇的狀態轉移規則如下：

POijOxy=

(24)

(25)

資源選擇的狀態轉移規則如下：

(26)

(27)

2.5 信息素更新

第i只螞蟻anti在搜索后，需要更新螞蟻地圖中所遍歷路徑的信息素。精英蟻群策略能使算法在收斂的同時具有較好的全局搜索能力和較高的搜索效率。工序選擇和資源選擇的信息素更新規則分別為

(28)

(29)

(30)

(31)

式中，Q為常數；ρ為信息素揮發系數；p為精英螞蟻路徑組合；t表示第t次迭代。

求解考慮關鍵件加工質量的雙資源約束的柔性作業車間調度問題的兩級嵌套蟻群算法的流程如圖4所示。

圖4 算法流程圖

3 實驗

為測試本文設計的兩級嵌套蟻群算法在求解考慮關鍵件加工質量DRCFJSP的性能，在CPU-I5 1.19 GHz、內存8.00 GB的PC機上使用Python 3.7.0編程運行和實現。算法參數設置如下：循環次數K=200，螞蟻總數Anum=30，信息揮發數ρ=0.1，初始信息素τ0=1，信息素啟發因子α=1，期望啟發因子β=5，P0=0.8，P1=0.8，P2=0.5，信息素增強系數Q=1。每個算例求解20次，每次求解過程中，當最優解連續10代不更新時，結束運行。

3.1 算例1

將文獻[11]給出的DRCFJSP實際應用案例作為算例1，在不改變原問題的基礎上，為保證算例符合本文問題，對算例重新進行描述，即將非機加工工序(鉗、熱處理、檢驗等)時間看作是后道機加工工序的準備時間，其余描述不變。

文獻[11]只考慮工人操作效率的異質性，未考慮工人操作每臺機床的實際合格率不同，于是，本文在原始算例的基礎上，增加了機床和工人操作某道工序的加工合格率(機床k加工合格率ρk、工人l操作機床k的熟練度ρlk)，工序加工時間、各工件的工序數量與原算例一致。數控機床(機床1、2)的加工合格率高于普通機床(機床3～8)，設機床1～8的加工合格率為(0.996，0.992，0.984，0.985，0.986，0.983，0.985，0.982)；工人需參與普通機床的整個加工過程，對工序的實際加工質量產生影響；工人只需參與數控機床的準備工作，對實際加工質量不產生影響，因此，根據文獻[11]對工人能力級別的區別系數，得到工人在各機床上的加工合格率矩陣：

E=[eij]8×8=

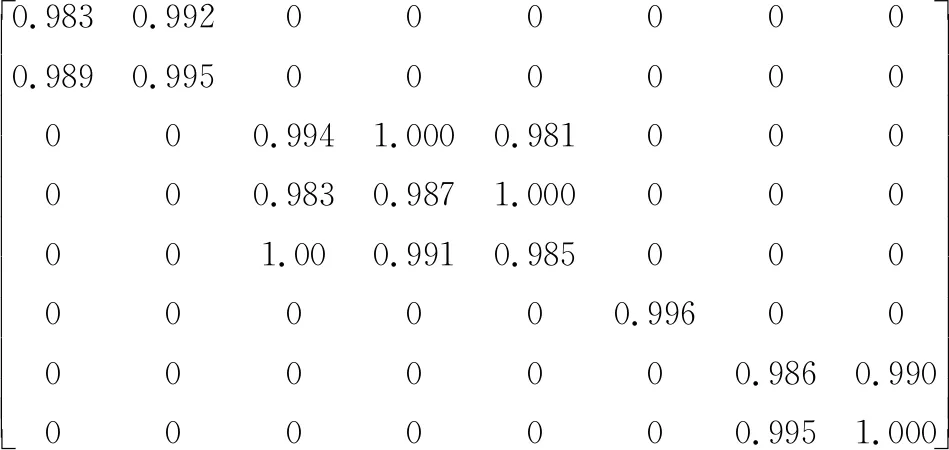
其中，elk為工人l操作機床k的加工合格率，elk=0表示工人l不可操作機床k。文獻[11]中，指定人員加工工件3、4、7、8的關鍵工序，于是本文選擇工件3、4、7、8為關鍵件。文獻[11]中關鍵工序指定特定工人加工，本文根據所給工人在各機床上的加工合格率矩陣，設定關鍵件3、4、7、8對應的工件加工質量閾值為(0.945，0.935，0.935，0.936)。

使用文獻[11]的保質策略，即不考慮工件的整體加工質量，只將關鍵工序指派給加工合格率較高的工人和機床組合進行生產，利用本文設計的兩級嵌套蟻群算法求解算例1，得到甘特圖(圖5)。圖5中，黑框表示準備時間，例如，機床1上工件8的第一道工序的準備時間為文獻[1]中工序1(鉗)的時間；彩色框和灰框為機加工工序，其中，灰框表示關鍵工序，虛線框①中的關鍵工序指派給工人8完成，虛線框②中的關鍵工序指派給工人2完成。最優調度解的完工時間為40.60，優于文獻[1]中的總完工時間42.62。本文增加的合格率評價僅用作工件加工質量的衡量，并未實際改變加工時間以及加工過程，且本文算法得到的最優解優于文獻[11]的最優解，因此本文提出的兩級嵌套蟻群算法在求解DRCFJSP上有更好的性能。

圖5 算例1的調度甘特圖

為進一步驗證考慮關鍵件加工質量的策略，將策略1(將關鍵工序指派給特定工人進行加工的保質策略[1])、策略2(整體保質策略[9])和本文策略進行對比，迭代結果如圖6所示，可以看出，在主要優化目標完工時間相同的條件下，策略2與本文策略的總體加工質量水平和關鍵件加工質量水平具有一定優勢，可見指派關鍵件/關鍵工序給特定工人進行加工并不能保證很高的整體加工質量和關鍵件加工質量；但策略2的總體加工質量水平高于本文策略，但策略2的關鍵件加工質量水平低于本文策略，可見本文所提策略在一定程度上能防止加工質量向非關鍵件偏移。

(a)完工時間 (b)總體加工質量水平 (c)關鍵件加工質量水平

各工件的加工合格率情況如圖7所示，策略2的一些非關鍵件如J1、J2、J5、J6的加工質量均高于本文策略最優解的加工質量，但關鍵件J3、J7的加工質量并沒有達到質量閾值，導致關鍵件加工質量得不到保障，可見只考慮整體加工質量會導致部分非關鍵件搶占關鍵件的優秀加工資源。本文策略得到的最優解中，所有關鍵件均能滿足加工質量的要求，因此本文策略有效。

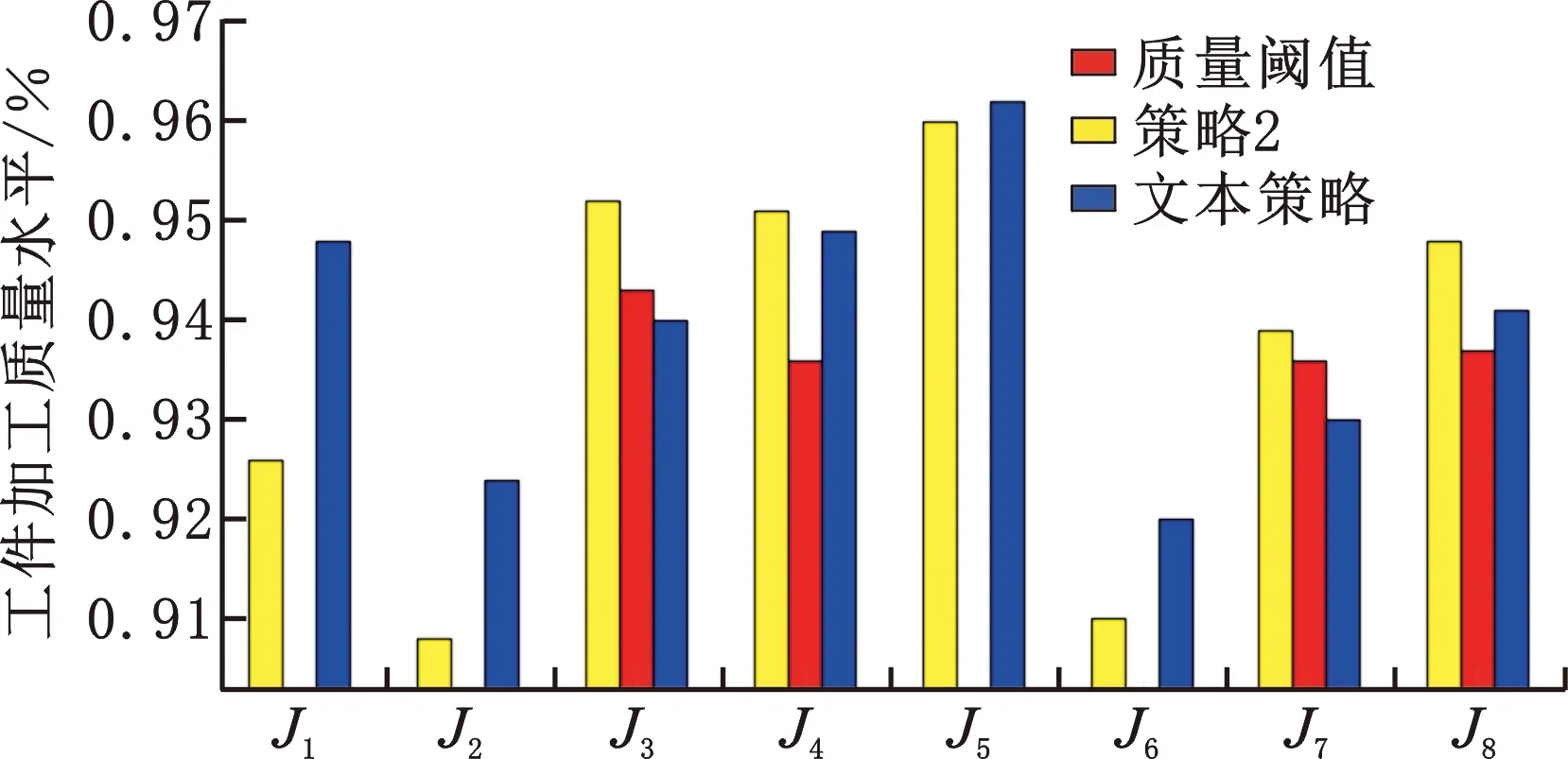
圖7 不同策略對應各工件加工質量柱狀圖

3.2 算例2

算例1規模太小，僅需很少的迭代就能收斂，且沒有考慮準備時間。為進一步驗證本文所提保質策略和兩級嵌套蟻群算法的可行性，在BRANDIMARTE[18]設計的FJSP算例mk01～mk10上增加了工人數量及各工人對應的可操作機器集[19]，形成算例2。根據本文問題的特點，增加以下條件：任選全部機床的30%為數控車床，工序準備時間服從U[2，8]的均勻分布；任選20%的工件為關鍵件，關鍵件加工質量服從U[0.93，0.95]的均勻分布；普通機床和工人的加工合格率服從U[0.98，1.00]的均勻分布，數控機床的加工合格率服從U[0.994，1.000]的均勻分布，以驗證算法的可行性。表1給出了mk01～mk10的具體延伸情況和算例的測試結果(含對應的關鍵件及其加工質量要求)。算例mk01的規模為10×6，即工件數n=10，機器數m=6，工人數為4，數控機床的機器編號為2和4，關鍵件的編號為1和4，對應的關鍵件加工質量要求分別為0.934和0.943，最優解的完工時間Cmax為56，整體加工質量水平Q為10.591，工件1～10的加工質量水平分別為0.946、0.957、0.947、0.947、0.949、0.950、0.933、0.945、0.951、0.942，關鍵件1的加工質量水平為0.946，關鍵件4的加工質量水平為0.947，均滿足對應的關鍵件加工質量要求。

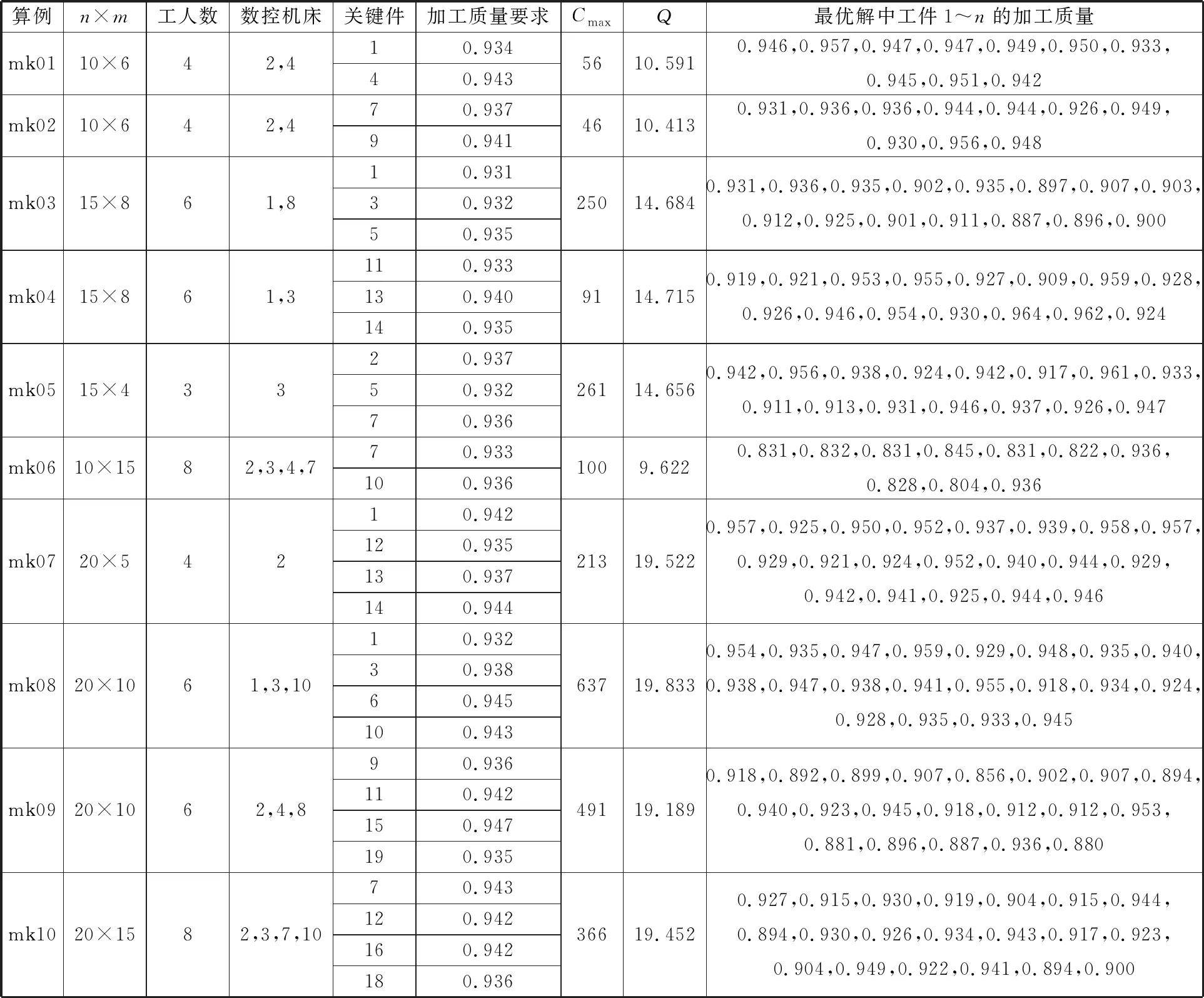
表1 算例2測試結果

由表1可以看出，各算例最優解得到的關鍵件的加工質量均能滿足其加工質量要求。圖8為算例2中mk01的迭代收斂圖，可以看出，隨著總完工時間的縮短，加工質量閾值一直上升，平均加工質量及最優解的加工質量都不斷上升并最終收斂，總完工時間的最優解為56，加工質量水平為22 369 740。由圖9(算例mk01的最優解的甘特圖)可以看出工人操作普通機床和數控機床在加工時間的差異。數控機床2加工工件2的第一道工序時，工人僅負責加工的準備工作外；普通機床3加工工件1時，工人除需完成準備工作，還需參與整個工件加工的過程。機器連續加工同一工件時，后道工序的準備工作可以省略，如機床2上工件8的最后兩道工序、機床1上工件6的相鄰兩工序。本文設計的兩級嵌套蟻群算法不僅可以解決考慮關鍵件加工質量的相關問題，還能避免工序間準備時間的冗余，以及人員在普通機床和數控機床之間的差異問題。

圖8 算例mk01迭代收斂圖

圖9 mk01調度甘特圖

4 結論

為解決雙資源約束柔性作業車間調度問題，本文考慮關鍵件的加工質量及整體工件加工質量，設計了帶保質策略的兩級嵌套蟻群算法。針對工人、機床時窗差異，以及工人操作普通機床和數控機床之間的差異，提出了一種基于時窗的活動調度策略。實驗分析了2種保質策略和考慮關鍵件的保質策略的整體加工質量水平與關鍵件加工質量水平的差異，發現在資源有限型車間內，考慮關鍵件的保質策略能夠更好地解決非關鍵件搶占關鍵件加工資源的問題。

加工質量問題是實際制造系統亟待解決的問題之一，本文目前解決的是靜態調度問題，后續將研究加工質量的動態調度問題，包括在動態加工的場景中如何實時跟蹤工件的加工質量，以及快速響應因加工質量變化帶來的調度決策，嘗試設計實時性和準確性更高的資源約束型生產調度算法。