基于遺傳學習人工蜂群算法的級聯多電平逆變器SHEPWM研究

陳施齊，王 英

(大連交通大學 自動化與電氣工程學院，大連 116045)

0 引 言

多電平逆變器因自身特殊的電路拓撲結構和控制方法，被廣泛應用于柔性輸電、泵、鐵路、電動汽車驅動系統等高壓大功率場合。相比于其他拓撲的多電平逆變器，級聯型H橋逆變器具有制造設計可模塊化、無需二極管箝位、相電壓冗余、有多個電壓源易于控制等優點。

特定諧波消除脈沖寬度調制(以下簡稱SHEPWM)作為多電平逆變器的常用調制方法，可以通過選擇開關時刻去消除特定的低次諧波，開關角由非線性方程組求得，因此非線性方程組的求解是SHEPWM技術的核心問題和研究熱點。文獻[1]提出將遺傳算法的交叉算子引入到人工蜂群(以下簡稱ABC)算法的觀察蜂階段，以增加非線性方程組解的多樣性；文獻[2]提出精英蜂群搜索策略來平衡ABC算法勘探與開發能力，達到高效尋優的目的；文獻[3]引入Tent混沌映射改進策略，提高ABC算法的全局尋優能力；文獻[4]采用禁忌搜索策略，在避免ABC算法早熟的同時，加快收斂速度；文獻[5]提出將多種群遺傳算法應用于多電平逆變器SHEPWM技術數學模型非線性方程組的求解；文獻[6-8]同樣著眼于算法，以優化SHEPWM技術開關角的求解。

本文將遺傳學習(以下簡稱GL)算法引入到ABC算法的偵察蜂階段，偵察蜂階段被拋棄的蜜源將由GL算法構建的新蜜源代替，用GL算法和ABC算法相結合的ABC-GL算法，解決SHEPWM求解非線性方程組問題，提高了ABC算法的求解精度，能更快速地迭代收斂。仿真結果驗證了ABC-GL算法的有效性。

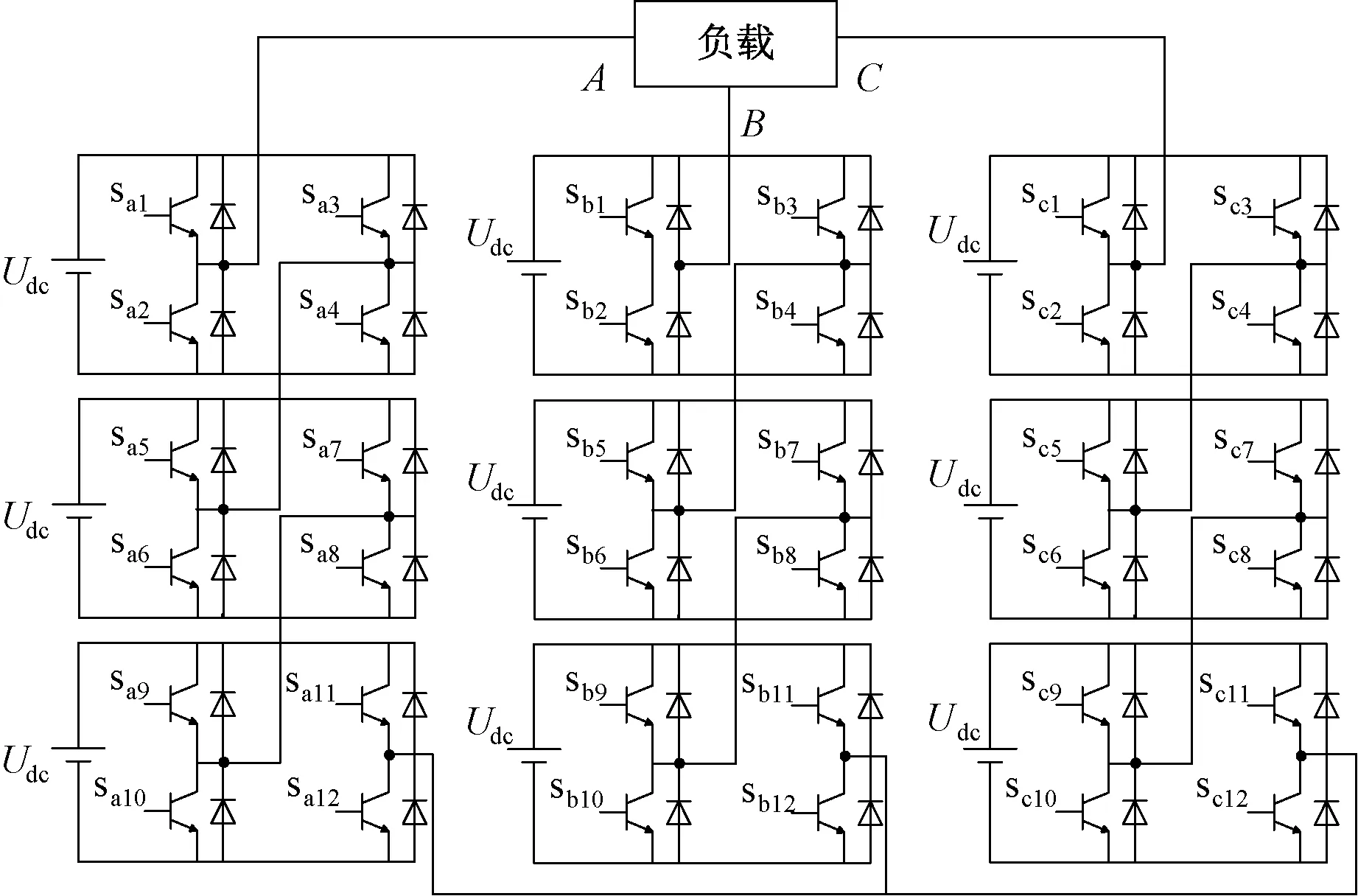
圖1 三相級聯型H橋七電平逆變電路拓撲

1 H橋七電平逆變器及SHEPWM原理

圖1為三相級聯型H橋七電平逆變電路拓撲，其中3個三電平H橋通過單元級聯的方式組成三相電路的其中一相，通過將下面的H橋單元輸出箝位到上面的H橋單元，達到單元輸出電壓疊加的效果。

表1為A相逆變電路輸出電壓與開關管開關狀態之間的關系。

從理論上看，SHEPWM可對任意逆變器輸出波形進行分析，為達到消除(N-1)個諧波的目的，需要選擇計算出N個開關角度。在實際情況中，為了盡可能減少諧波，使輸出波形易于控制，應盡量使波形具有對稱性。為了消除偶次諧波，應使波形正負兩半周期鏡對稱；為了消除諧波中的余弦項，應使波形在正半周期內前后1/4周期以π/2為軸線對稱。圖2為2k+1電平的階梯波，其中k為T/4內開關角個數。

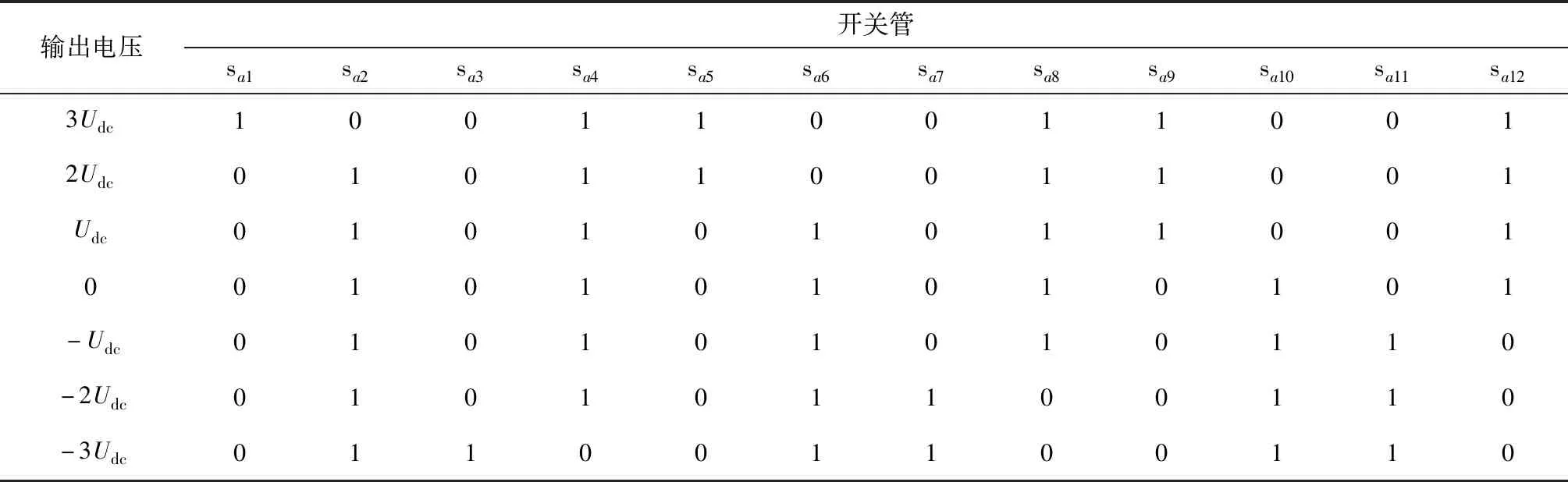
表1 H橋型七電平逆變器A相輸出電壓與開關管開關狀態之間的關系

對圖2波形進行傅里葉級數分解，可得：

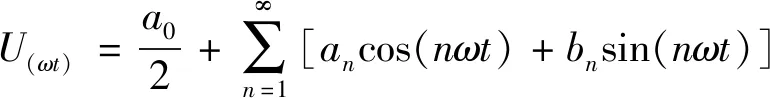
(1)

(2)

經過奇偶性及對稱性處理后，該波形的基波及各次諧波可以化簡：

(3)

式中：U(ωt)為輸出電壓；n=1,2,3,…；U(dc)為H橋單元直流側電壓；ω為角頻率；αi為第i個開關角度；k為1/4周期內開關角度數。開關角度應滿足:

(4)

令待消除諧波的幅值為0，可以得到關于α的非線性方程組。

2 ABC-GL算法

ABC算法受蜂群尋找優質蜜源行為的啟發，通過蜜蜂個體反復比較蜜源質量的好壞確定全局最優。ABC算法結構簡單、參數少、魯棒性強、探索能力強，但容易陷入局部最優。GL算法借鑒生物種類的遺傳進化過程，根據定義的適應度，通過全局搜索更新適應度最高的新個體，存在交叉、變異、選擇操作。

類似于傳統ABC算法的總體運行過程，ABC-GL算法先用ABC算法生成一個分布較優的初始種群，在ABC的偵察蜂階段引入GL算法，對于ABC的每次迭代，對于每個符合試探次數Ti>L的蜜源i，都進行GL算法里的交叉、變異、選擇操作。ABC-GL算法中，SN是初始種群數量，每個蜜源的位置xi,j=(xi1,xi2,…,xiD)代表優化問題的一個可能解，其中i∈{1,2,…,SN}，D是待優化問題維數，蜜源的花蜜量對應于相應解的質量或適應度值fiti。

ABC-GL算法的流程如下。

1)由式(5)隨機初始化生成含有SN個初始解的種群，根據式(5)隨機初始化生成初始人工蜂種群。

xi,j=xmin,j+rd(xmax,j-xmin,j)

(5)

式中：rd為[0，1] 之間的隨機數；xmin,j與xmax,j分別為第j維變量的下界與上界。

2)計算每個蜜源的適應度值fiti。

3)雇傭蜂階段：雇傭蜂通過式(6)對蜜源進行搜索更新，生成候選解vi=(vi1,vi2,…,viD)，并計算新的適應度值fiti，若優于原來的適應度值則替換xi。

vi,j=xi,j+φi,j(xi,j-xk,j)

(6)

式中：φi,j為[-1，1]之間的隨機數，k∈{1,2,…,SN}是隨機選取的一個蜜源，且滿足k≠i，j∈{1,2,…,D}是隨機選取的一個維。

4)觀察蜂階段：觀察蜂按照式(7)的選擇概率對雇傭蜂發現的蜜源進行進一步搜索開采。

(7)

5)偵察蜂階段：若一個雇傭蜂對應的蜜源xi經過L次開采搜索仍沒有成功更新，則對應的雇傭蜂成為偵察蜂，采用式(8)重新隨機初始化搜索一個新的蜜源代替xi。

xi,j=xmin,j+rand(0,1)(xmax,j-xmin,j)

(8)

6)記住全局最優解gbest。

7)交叉操作：對于每個被拋棄的蜜源xi，根據sol=[sol1,sol2,…,solD]生成一個子代。

隨機抽取當前蜂群里的兩個蜜源，其序號為s1、s2,s1≠s2≠i，令：

(9)

(10)

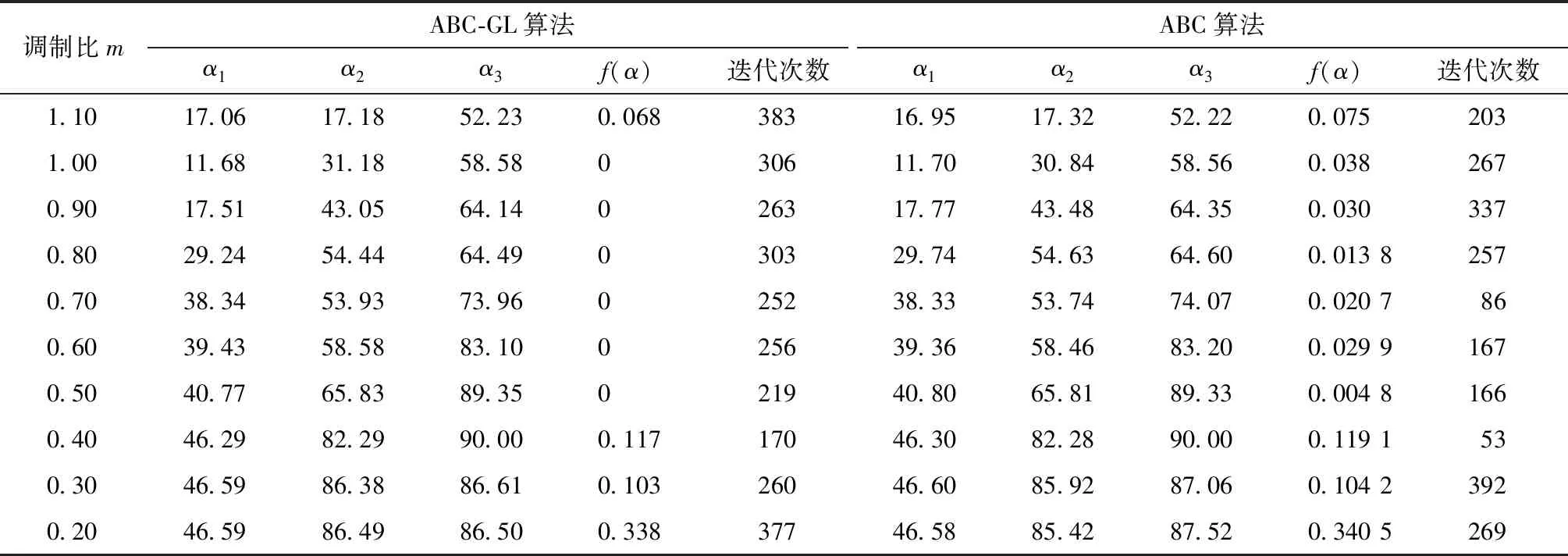
8)變異操作：使用變異概率pm對sol的每一維進行隨機變異操作。對于sol的第d維，若rd

sold=Xmin,d+rd(Xmax,d-Xmin,d)

(11)

9)選擇操作：產生的子代sol將與被拋棄蜜源xi競爭，若找到的sol優于xi，則提前結束GL過程；反之則重復偵察蜂過程Tmax次，直到找到更優蜜源sol。若經Tmax次都未找到，則取已產生的最優xi作為新蜜源，這樣可以確保新蜜源大多數時候不會發生退化現象。

10)計算偵察蜂階段的適應度值fiti，若優于原來的適應度值則用新的蜜源替代原來的蜜源，算法終止，生成3個最優開關角，輸出gbest，否則回到流程(3)。

3 SHEPWM開關角度求解

當k=3時,逆變器輸出電壓波形為七電平的階梯波，式(3)可以消除兩種特定諧波，由輸出波形的對稱性及三相電壓之間的相位關系，只需要消除6a-1,6a+1次諧波(a=1,2,3,…)，故令5、7次諧波幅值為0，定義基波調制度:

(12)

式中：U為基波幅值。令:

(13)

由此，建立算法的適應度函數f(α):

(14)

由上式可知，SHEPWM開關角求解問題被轉化為一個單目標問題，當f(α)最小時，ε1、ε2、ε3均為最小，此時求出的開關角度即為式(13)的解。

為驗證ABC-GL算法求解非線性方程組的性能優于改進前的ABC算法，在調制比m相同的情況下比較兩種算法求得的開關角度、f(α)和迭代次數。其中ABC的參數：初始種群數量SN=100，D=3，迭代次數400。ABC-GL的參數：初始種群數量SN=200，D=3，單點變異概率pm=0.005，最大試探次數Tmax=20，迭代次數400。不同調制比下，兩種算法的比較結果如表2所示。由此可以得出，通過ABC-GL算法運算生成的f(α)更接近0，且進化時間更穩定，證明ABC-GL算法比ABC算法更適合用來求解SHEPWM方程組。

表2 各調制比下兩種算法指標比較

4 H橋七電平逆變器仿真分析

在MATLAB仿真平臺上，從表2的數據中選取5組值，得到目標函數適應值與迭代次數的關系，如圖3所示。

圖3 目標函數適應值與迭代次數的關系

由圖3可見，在目標函數適應值相同的前提下，ABC-GL算法在5次迭代計算中的迭代次數少于改進前的ABC，算法的計算量減小。ABC-GL算法計算出的目標函數適應值均無限接近0，而ABC算法在5次迭代計算中目標函數適應值均不同，且優化精度低于ABC-GL算法。ABC-GL算法在迭代200次左右時已基本得到全局最優解，而ABC算法迭代次數比較分散，可見ABC-GL算法的進化過程比ABC算法穩定。由此可知，ABC-GL算法更適合用來求解目標函數。

為了驗證上述理論分析及改進算法求解方程組的正確性，本文在Simulink環境下搭建三相級聯H橋七電平逆變器，用SHEPWM控制輸出開關角度。圖4、圖5分別給出了調制度m=0.9時ABC算法和ABC-GL算法輸出相電壓UAN和線電壓UAB的波形及FFT結果。

從上述仿真圖可以看出，傳統的ABC算法不能較好地消除5次和7次諧波，而經過GL改進的ABC算法，5次諧波與7次諧波的消除效果較好，線電壓和相電壓的THD值較為理想，可以驗證用ABC-GL算法解決SHEPWM求解非線性方程組問題是正確有效的。相電壓的3次諧波較改進前有些許增加，表明該算法在解決消除5次和7次諧波問題的同時仍有不足。由于相位關系的存在，三相線電壓中3的倍數次諧波被消除，故符合理論預期。

5 結 語

本文針對ABC算法應用于多電平逆變器SHEPWM技術開關角度值求解時容易陷入局部最優，引入ABC與GL結合的算法，在符合ABC求解效率前提的同時，有效地提升了ABC算法的全局搜索能力和尋優精度，減小了ABC算法的計算量，并將ABC算法與ABC-GL算法進行仿真對比，結果驗證了ABC-GL算法計算的開關角度值是正確有效的，輸出電壓可以達到理想效果。