地下水中污染物溶質運移模擬

喻 佳 魏善彪 麻勝坤

（1．江西核工業環境保護中心，江西 南昌 330002；2．江西省地質局實驗測試大隊，江西 南昌 330002；3．萬載紅獅環保科技有限公司，江西 宜春 336100）

0 引言

在建設項目運行過程中出現非正常工況，導致廢液或廢水泄漏后，進入土壤及地下水環境中，會對土壤及地下水環境造成污染。《環境影響評價技術導則 地下水環境》（HJ 610—2016）的評價對象為地面以下飽和含水層中的重力水，未考慮非飽和帶對廢液或廢水的吸附、彌散、降解等作用。該文以某火電廠脫硫廢水收集池為例，利用GMS中FEMWATER模塊將研究區飽和及非飽和帶作為一個整體進行模擬計算，評價廢水泄漏后對地下水環境的影響。

1 FEMWATER模擬求解原理

FEMWATER為基于三維有限元的計算模式。有限元法為采用“分片逼近”方法求解水流、溶質運移耦合的偏微分方程。該求解方法的原理如下：假設模擬范圍是由很多很小的可是彼此聯系的三維的多面體單元組成的，各個單元的頂點稱為節點，不同單元之間則通過節點進行聯系；先采用變分法或加權剩余法來建立各節點單元的系數矩陣，對各單元進行離散求解，然后將各單元矩陣集合，合并成描述整個求解范圍的方程組，同時把邊界條件歸并到總矩陣中，進而建立整個求解范圍的系數矩陣，用FEMWATER中的求解器對方程組進行求解，最后得出結果。

因此，FEMWATER數值模擬的原理為在一定的初始、邊界條件下，用三維有限元法對多孔介質中的飽和-非飽帶的水流及溶質運移方程進行求解。下面介紹水流和溶質控制方程。

1.1 地下水水流運動控制方程

地下水水流運動控制方程如公式（1）所示[1]。

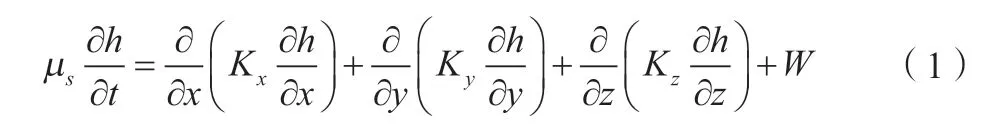
式中：μs為貯水率，1/m；h為水位，m；Kx、Ky、Kz分別為x、y、z方向上的滲透系數，m/d；t為時間，d；W為源匯項，m3/d。

1.1.1 初始條件

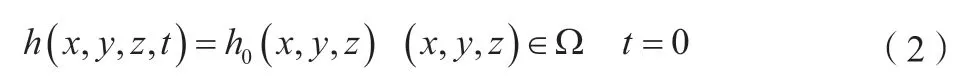
式中：h0（x，y，z）為已知水位分布；Ω為模型模擬區域。

1.1.2 邊界條件

第一類邊界如公式（3）所示。

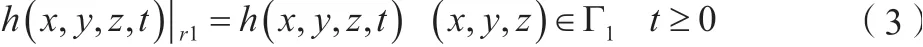
式中：Γ1為一類邊界；h（x，y，z，t）為一類邊界上的已知水位函數。

第二類邊界如公式（4）所示。

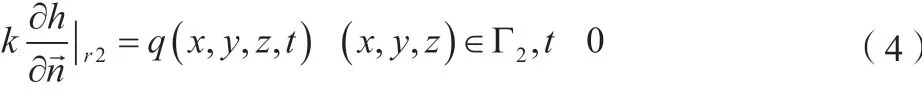
式中：Γ2為二類邊界；k為三維空間上的滲透系數張量；為邊界Γ2的外法線方向；q（x，y，z，t）為二類邊界上的已知流量函數。

第三類邊界如公式（5）所示。

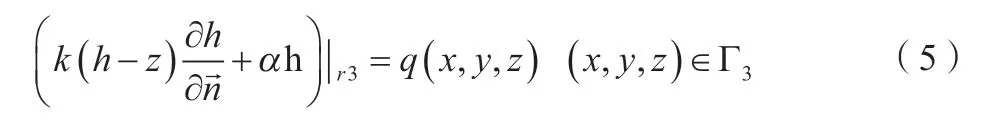
式中：α為已知函數；Γ3為三類邊界；k為三維空間上的滲透系數張量；為邊界Γ3的外法線方向；q（x，y，z）為三類邊界上的已知流量函數。

1.2 溶質運移控制方程

溶質運移控制方程如公式（6）所示[2]。

式中：R為遲滯系數，量綱為1。為介質密度，kg/（dm）3；θ為介質孔隙度，無量綱；c為組分的濃度，g/L；為介質骨架吸附的溶質濃度，g/kg；t為時間，d；x、y、z為空間位置坐標，m；Dij為水動力彌散系數張量，m2/d；vi為地下水滲流速度張量，m/d；W為水流的源和匯，1/d；Cs為組分的濃度，g/L；λ1為溶解相一級反應速率，1/d；λ2為吸附相反應速率，1/d。

1.2.1 初始條件

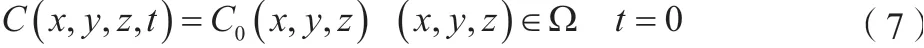
式中：C0（x，y，z）為已知質量濃度分布；Ω為模型模擬區域。

1.2.2 邊界條件

第一類邊界為Dirichlet條件，即指定邊界濃度；第二類邊界為Neumann條件，即指定邊界上的濃度梯度；第三類邊界為Cauchy條件，即同時指定邊界濃度以及邊界上的濃度梯度，也就是第一類邊界條件與第二類邊界條件的結合。

基于FEMWATER可運用三維有限元法對飽和及非飽和帶多孔介質中的水流及溶質運移進行求解，國內不少學者利用其進行研究[3-4]。

2 研究區概況

該文以某火力發電廠脫硫廢水收集池為例進行研究。根據研究區工程勘察報告，其地層自上而下為雜填土，層厚1.00m～2.80m；粉質黏土，層厚約1.20 m～4.10 m，局部夾薄層灰黃色粉土、粉砂；淤泥質黏土，層厚0.90 m～3.50 m；粉細砂，層厚約35.0 m；中砂，層厚約7.10 m～13.50 m；泥質砂巖，此層未揭穿。地下水類型主要包括松散巖類孔隙水及紅層孔隙裂隙水。松散巖類孔隙水由第四系沖積成因的粉質黏土、粉細砂、砂礫石及卵礫石組成，由于表層發育一定厚度的淤泥質和粉砂質黏土層，使其潛水含水層具有微承壓性，含水層厚度一般為30m～40m；紅層孔隙裂隙水由于巖石泥質含量較高，抗風化能力差，裂隙多被充填，因此地下水富水性為貧乏。

3 數值模型

3.1 水文地質概念模型

水文地質概念模型為將研究區域地下含水系統的邊界、內部的含水層結構、地下水水動力和化學特征、滲透系數等水文地質參數的空間分布以及補徑排條件等概化為便于轉換為數值模型的基本模式。

該文根據研究區地下含水系統特征建立水文地質概念模型。首先，確定研究區模擬邊界。邊界條件概化為研究區位于平原區，水文地質條件較簡單，取西北側等水位線為西北邊界，該邊界為透水邊界，反映上游地下水對本研究區域的補給；東南方向的長江劃定為排泄邊界，作為第一類邊界；兩側邊界垂直于等水位線，劃定為零通量邊界；取模型表層為上邊界，接受大氣降水的入滲補給，取為第一類邊界；模型底部為泥質砂巖，該邊界劃為零通量邊界。源匯項：研究區內地下水主要是接受大氣降水的入滲補給，主要排泄方式為流入長江，伴有少部分的潛水以蒸發方式排泄。研究區域水文地質較簡單，在水平方向上不進行參數分區；根據水文地質剖面圖及其顯示的地下水含水層巖性分布情況，模型概化為潛水-微承壓含水層，垂向上分為3層，自上而下0 m～5 m為雜填土粉質黏土、淤泥質黏土，5 m～45 m為粉細砂、中砂，45 m～53 m為泥質砂巖。

3.2 用TIN生成三維網格

GMS為FEMWATER提供了用TIN生成三維網格、由實體（Solid）模型產生三維網格、由節點產生三維網格、直接由Modflow有限差分網格轉為三維有限元網格，共4種可生成三維有限元網格的方式。該研究采用TIN生成三維網格方法。

TIN生成三維網格利用二維網格（2-Dmesh）模塊及三角形不規則網格剖分（TIN）模塊一起生成三維網格（3-Dmesh），該方法可相對比較方便及快速自動生成大范圍的三維網格，局部網格還可以根據需要使用GMS提供的工具進行加密等處理。由于二維網格（2-Dmesh）是三維網格（3-Dmesh）在x-y平面上的投影，因此，需要先生成二維網格（2-Dmesh）。首先，在確定好的多邊形（研究區）上建立二維網格（2-Dmesh），然后再將二維網格（2-Dmesh）轉換為一對TIN，這一對TIN在x-y平面上必須保持一致，否則生成三維網格（3-Dmesh）會出錯，無法生成三維網格。可以通過數據點的高程差值或者輸入一個確定的高程值來確定TIN的高程值，這一對TIN中間的區域就是在這一層上所要建立的三維網格（3-Dmesh）區域。然后選中這一對TIN，使用TINS菜單中的FILL BetweenTINS-＞3-Dmesh就可以生成所要的三維網格[5]。

研究區三維網格生成情況如圖1所示。

圖1 研究區平面、垂向網格剖分圖

由圖1可知，創建網格時對局部研究區域進行加密，可使預測結果更精確。

3.3 水流數值模型識別與校正

概化的水文地質概念模型，通過FEMWATER界面轉化的水流數值模型，須反映研究區域實際流場情況。因此，進行水質模擬預測前，必須對水流模型進行識別、校正，主要是對其參數以及邊界條件等進行校正，源匯項包括降水及蒸發等。本次模擬使用的是多孔介質模型，將研究區概化為非均質、各項同性、空間三維結構、非穩定地下水流。根據水文地質資料，初步選定的參數較客觀地反映研究區實際的流場情況，加之細致地調參進行模擬后，校正后的模型取得了符合要求的效果。研究區參數見表1。

表1 模型計算主要參數一覽表

3.4 水質模型條件的概化

水流模型經識別校正滿足要求后，進行溶質模擬前，需要輸入水質模型相關參數。通常，以評估潛在的污染源為目的的許多溶質遷移問題都將地下水中污染物濃度設為0；因此，本次水質模型將地下水中氟化物初始溶度設為0。模型將污染源以面源形式設定濃度邊界，污染源位置按實際設計概化，并在污染源位置處對網格進行加密處理。在模擬污染物擴散時，不考慮吸附作用、化學反應等因素，重點考慮了對流、彌散作用。

3.5 預測情景

模擬情景設置為在有防滲條件下，脫硫廢水收集池防滲破損5%發生泄漏情景下污染物運移模擬。

3.6 預測源強

由于建立的模型沒有考慮吸附作用及化學反應等因素，因此在其他條件（包括水動力條件、彌散及泄漏量等）相同的情況下，污染物在地下水中的擴散主要由污染物初始泄漏濃度決定。污染物濃度的高低是相對的，該文以超標倍數這個參數選擇預測因子。根據脫硫廢水收集池中污染物超標倍數情況，該文選取氟化物為預測因子。在防滲破損情況下，脫硫廢水收集池氟化物濃度取50 mg/L。

3.7 泄漏時間確定

脫硫廢水收集池下游約30 m處設置了觀測井，假定廢水持續泄漏，觀測井中監測到地下水中氟化物濃度約在273天出現超標，結合監測井每逢單月監測一次的監測頻率，確定泄漏時間為330天。

3.8 預測時間

根據電廠運行年限，確定預測時間為7300天。預測污染物泄漏后第100天、第860天、1000天、7300天氟化物在地下水中運移情況。

4 預測結果

將校正后的水流模型帶入水質模型進行模擬計算，得到氟化物在地下水中運移的計算結果（圖2～圖3），以下各圖說明了廢水泄漏第100天、860天后氟化物在地下水中水平及垂向上的運移情況。氟化物污染物模擬期內運移距離及濃度隨時間變化見表2。

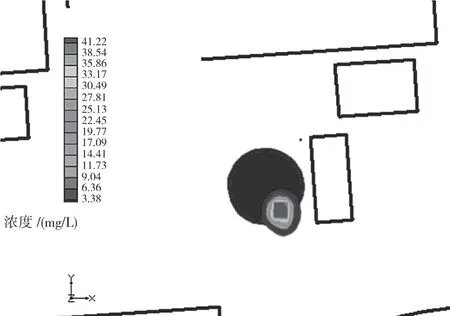
圖2 廢水發生泄漏后，第100天地下水中氟化物濃度分布

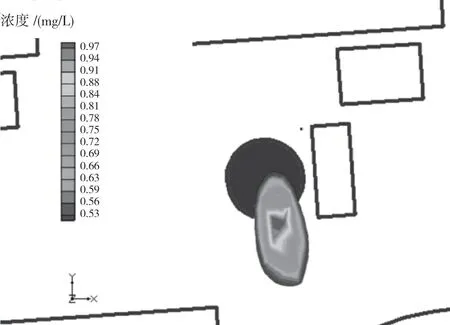
圖3 廢水發生泄漏后，第860天地下水中氟化物濃度分布

表2 不同時間地下水中氟化物運移距離及濃度情況

由圖2可知，氟化物發生泄漏后，由于廢水持續泄漏，氟化物在地下水對流及彌散作用下，向各個方向擴散，泄漏面源中心點處氟化物濃度最大，為43.91 mg/L，中心點水平運移距離為0 m。

由圖3可知，廢水泄漏330天后不再發生泄漏，運移至地下水中氟化物為僅有的污染源在地下水對流及彌散作用下，向各個方向擴散，由于不再有泄漏源強進入地下水中，污染羽中心點在地下水對流的作用下向下游遷移，遷移距離為6.38 m，中心點處氟化物濃度最大，為1.0 mg/L，將至標準限值；垂直方向上，氟化物對承壓層地下水影響相對較小。由于氟化物濃度將至限值1.0 mg/L，對環境影響很小，因此，未對第1000天、7300天進行評價。根據模型計算結果可知，自860天后，地下水中氟化物濃度逐漸降低，直至降為0。

分析不同時間氟化物在地下水中運移范圍可知，在平面上氟化物主要向地下水下游擴散，范圍相對較小，在水動力條件及彌散作用下，廢水泄漏后地下水中氟化物的遷移對潛水、微承壓含水層地的影響在廠區內。

5 結論

該文使用FEMWATER模塊對研究區域進行三維有限元的數值模擬計算，利用GMS軟件的圖像處理功能，將模擬結果可視化輸出，操作直觀簡便。

該文利用FEMWATER對研究區飽和-非飽和帶作為一個整體進行模擬計算，通過概化的模型，基于水流控制方程、溶質控制方程的耦合，可視化的輸出結果較為完整地呈現了污染物泄漏后，在飽和-非飽和帶中的遷移情況。

建議將土壤環境與地下水環境作為一個整體，結合地下水監控井確定廢液或廢水泄漏時間，評價污染物對土壤及地下水環境的影響。