兆瓦級雙饋風力發電機負載附加損耗分離方法研究

李 華

（中車株洲電機有限公司，湖南 株洲 412000）

0 引言

隨著齒輪箱技術更新與迭代速度逐漸加快，與之相匹配的雙饋風力發電機單機功率也逐漸提高，現階段已達到 10 MW等級[1]。兆瓦級大功率或超大功率雙饋風力發電機附加損耗的分離與準確計算一直是業內的瓶頸問題之一。準確分離與計算附加損耗對磁熱耦合精益設計、成本控制等方面均具有積極意義。該文以 1 臺 7 MW 等級 10.5 kV 雙饋風力發電機為計算案例，討論了一種解析—有限元相結合的附加損耗分離與計算方法，可為該類型電機的設計提供參考。

1 負載附加損耗的分離依據及其計算方法

1.1 負載附加損耗的分離依據

針對負載附加損耗的計算，要根據電機設計理論判斷在負載狀態下附加損耗的降落位置。位置 1：定子繞組漏磁場在槽內繞組及繞組端部附近的金屬部件。對兆瓦級雙饋風力發電來說，定子繞組通常匝數較少，并且電機設計通常為細長形式。根據電機設計理論可知，在繞組匝數較少且鐵心較長的情況下，繞組端部漏抗越低，對電機運行的影響越小[2]。那么針對這種類型的電機，定子繞組附加損耗只需要考慮槽內部分。位置 2：定子磁動勢諧波所產生的磁場在轉子導條（或鼠籠）感生電流引起的附加損耗。為了提高轉子運行的可靠性、降低發電機成本，兆瓦級雙饋風力發電主流的技術路線已經朝銅條波繞組形式轉化[3]。轉子線圈采用單匝線棒形式，因此在磁動勢諧波相對復雜的條件下，需要準確計算轉子繞組的附加損耗。位置 3：氣隙諧波磁場在鐵心表面造成的表面損耗與齒中造成的脈振損耗。雙饋電機本身的勵磁形式屬于柔性勵磁，其定子和轉子中通常有頻率不同的三相電流，這就導致氣隙中的諧波成分更復雜[4]。當諧波波長比鐵心凹凸面的間距小很多時，諧波磁通集中在鐵心表面，造成表面損耗；當諧波波長比鐵心凹凸面的間距大很多時，諧波磁通會透入齒、軛，形成閉合磁路，從而造成脈振損耗。那么在兆瓦級雙饋電機中，以上2 種損耗都需要根據具體位置進行計算與分離。

1.2 不同位置附加損耗計算方法

1.2.1 定子繞組槽內附加損耗計算

定子線圈通常采用多跟并繞形式，如果直接采用有限元計算，就難以滿足工程的相應需求。經過對比計算驗證，采用《電機設計》中的解析計算公式就可以基本滿足工程需求，那么由渦流效應造成的定子電阻增加系數如公式（1）所示。

式中 ：m為槽高方向導體數 ；n為寬度方向并繞根數 ；b為線規寬度 ；bs為定子槽寬 ；f為電機工作頻率 ；a為線規高度 ；ε為長度系數，為簡化計算可初步選取ε=5/6。

1.2.2 轉子導條（或鼠籠）感生電流引起的附加損耗

轉子導條采用單匝波繞組形式，因此在有限元計算中可以將導條及其絕緣按照 1 ∶ 1 的比例進行建立，并且為了充分考慮轉子導條的集膚效應，需要將導條表面網格進行加密處理，如圖 1 所示。

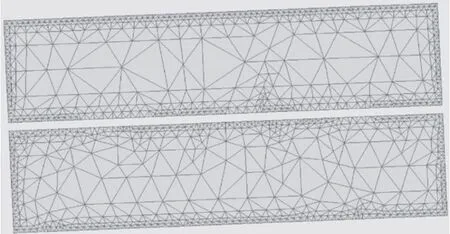
圖 1 轉子導條表面加密剖分

表面剖分深度如公式（2）所示。

式中 ：μ為相對磁導率 ；ω為電磁波角頻率，角頻率的給定取決于所需考慮的諧波次數 ；γ為計算溫度下對應的導體電導率。

在有限元計算中針對實體繞組線棒，計算結果會輸出線棒直流銅耗與交流銅耗的總體值[5]。進一步對直流銅耗與附加損耗進行分離。轉子線棒直流電阻如公式（3）所示。

式中 ：ρt為工作溫度下電阻率 ；N2為每相串聯匝數 ；lef為鐵心有效長度 ；Nt2為繞組并繞根數 ；Ac2為單根線棒截面積 ；a2為并聯支路數。

1.2.3 氣隙諧波磁場在鐵心中造成的附加損耗

在有限元中，分別對鐵心表面、鐵心齒部以及鐵心軛部進行分離，如圖 2 所示。

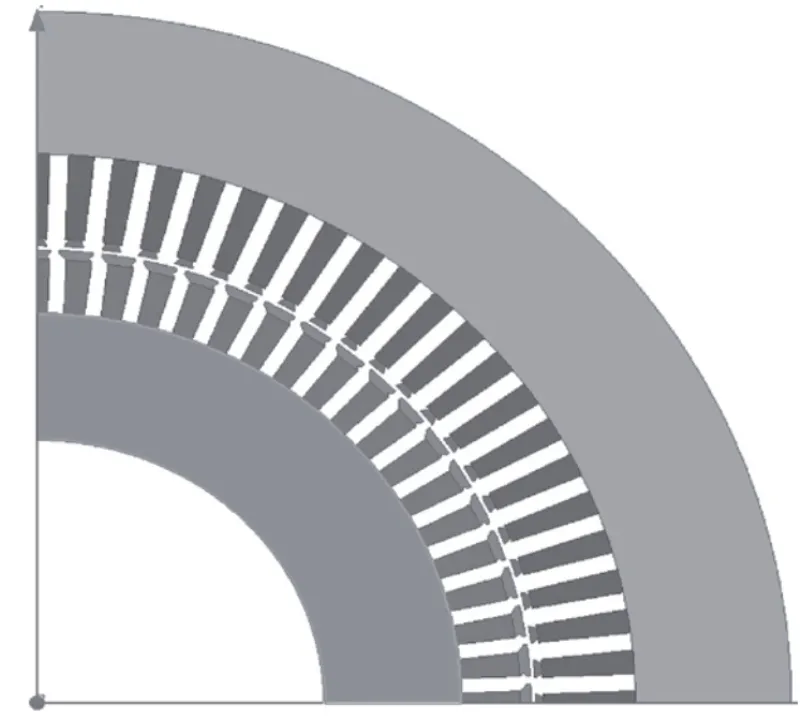
圖 2 鐵心各位置分離

采用解析—有限元相結合的方式計算各部分的鐵耗。在有限元計算中，鐵耗計算以 Bertotti 常系數三項式為計算基礎，軟件中任意磁密波形單位體積鐵耗瞬態時域方程標準形式如公式（4）所示。

式中 ：kh為磁滯損耗系數 ；kc為渦流損耗系數 ；ke為附加損耗系數Kdc為直流偏磁滯損耗系數 ；Bdc磁密直流分量 ；Bm為磁密 ；t為時間 ；Ce為鐵耗波形系數。

根據鐵耗瞬態時域方程分析，在實際有限元計算中，已經將鐵心中基本鐵耗與附加損耗計算在內，再對基本鐵耗與鐵心附加損耗進行分離。針對基本鐵耗的計算，采用經典解析法即可滿足工程實際需求。根據電機設計理論，對齒聯軛結構軛中的基本鐵耗計算如公式（5）、公式（6）所示。

式中 ：phej為軛部損耗系數 ；P10/50為當B=1.0 T、f=50 Hz 時，硅鋼單位質量內的損耗 ；Bj為鐵心軛部的最大磁通密度；pFej為軛部基本鐵耗；ka為矯正系數，ka=1.3 ；Gj為軛部質量。

齒中基本鐵耗計算如公式（7）～公式（8）所示。

式中 ：phet為齒部損耗系數 ；Bt為齒部磁路長度上磁通密度平均值；pFet為齒部基本鐵耗 ；ka為矯正系數，ka=1.8 ；Gt為齒部質量。利用解析法求取齒、軛部分的基本鐵耗之后，即可結合有限元計算結果進一步求取各部分的附加損耗。

2 7 MW-10.5 kV 雙饋風力發電機設計及損耗分離計算

2.1 發電機基本參數

該文基于一臺7 MW-10.5 kV高壓雙饋風力發電機展開設計[2]，并利用以上原理性方法對負載附加損耗進行分離計算。為用戶提供的電機的輸入技術參數見表1。電機設計主要參數見表 2。

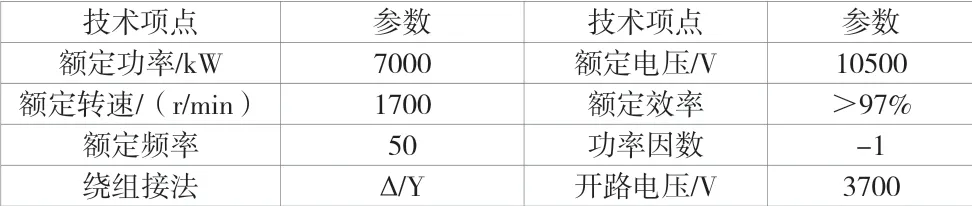
表 1 7MW 高壓雙饋風力發電機輸入技術參數

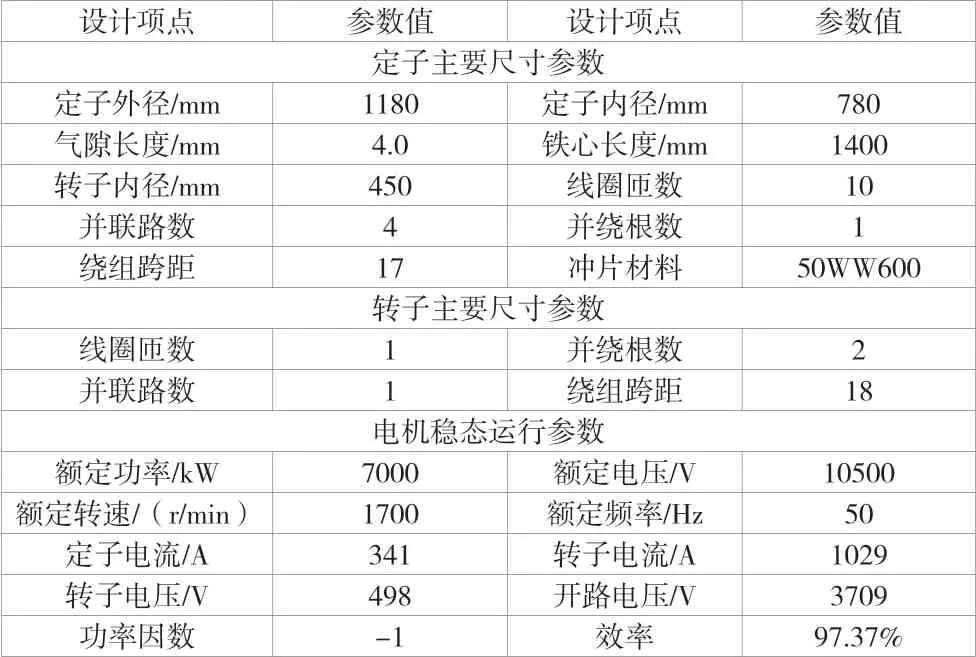
表2 7MW高壓雙饋風力發電機主要設計參數

設計過程中以用戶給定的性能要求為邊界條件，兼顧電機質量和體積，盡可能將該款電機設計為緊湊化結構，提高整機功率密度和性價比。

2.2 發電機負載附加損耗分離計算

針對以上設計參數，并結合前文所述的原理方法，對該款電機負載態下附加損耗進行分離[5-6]。

2.2.1 基本損耗計算

定子基本銅耗如公式（9）所示。

轉子基本銅耗如公式（10）所示。

鐵心基本鐵耗的計算以公式（5）～ 公式（8）為計算依據。其中，Bj與Bt需要結合有限元進行提取。負載態下磁密分布云圖如圖 3 所示。

圖3 負載態磁密分布云圖

通過磁密分布云圖分析，主磁路磁密分布符合電機設計的基本規律，有利于對鐵心內基本鐵耗分布進行控制。

鐵心軛部最大磁密Bj以相鄰極之間的中性面處作為提取位置，此處為兩極之間磁通匯聚最大的位置。因此，此處為鐵心軛部磁密最大的位置。齒部平均磁密Bt的選擇以磁密最大齒為目標，先對全齒所有網格點磁密進行積分處理，再除以全齒體積，以求取其平均磁密[6]，如公式（11）所示。

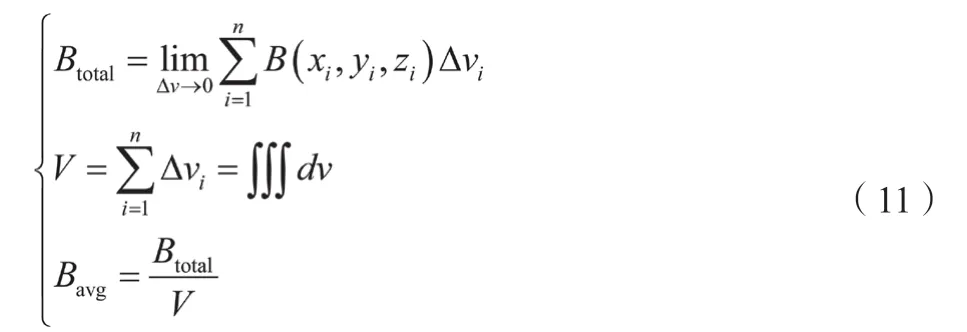
式中 ：Btotal為體磁密大小 ；xi為x方向單位長度 ；yi為y方向單位長度 ；zi為z方向單位長度 ；Δvi為體積增量 ；V為體積 ；dv為單位體積 ；Bavg為平均磁密大小。

根據以上計算原則與計算方法，由有限元提取的各部分磁密數值，見表 3。

表3 鐵心各部分磁密值分布

通過查找武鋼材料樣本手冊 50WW600 材料屬性可知，P10/50=1.702 W/kg。根據電機設計尺寸計算鐵心各部分質量，見表 4。

表4 鐵心各部分質量

根據公式（5）～公式（8）的計算原理可知，定子齒、軛部分的基本鐵耗見表 5。

表5 鐵心各部分基本鐵耗值分布

2.2.2 附加損耗的分離與計算

考察鐵心中的損耗分布密度，如圖 4 所示。分析負載狀態下鐵心損耗密度分布云圖，鐵心表面（定、轉子齒頂）損耗密度極大，根據上文對附加損耗分布位置的分析，可以認為鐵心表面部分的鐵耗全部由附加損耗構成。鐵心齒部損耗密度也存在變大的趨勢，根據上文分析可知，齒部損耗由基本鐵耗與脈振損耗構成。鐵心軛部損耗密度最均勻，但是造成脈振損耗的諧波磁場會經過鐵心軛部而形成閉合回路，因此鐵心軛部同樣要考慮脈振損耗的影響。根據有限元計算得到的各部分鐵耗值，見表 6。

圖4 負載狀態下鐵心損耗分布云圖

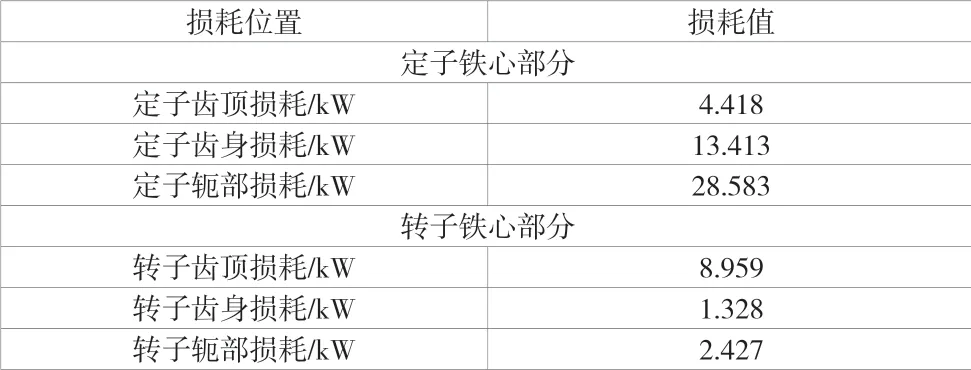
表6 鐵心各部分總損耗值分布

結合以上有限元計算結果與解析計算結果，可進一步分離鐵心各部分的附加損耗 ：1）將鐵心表面全部看作附加損耗范疇。2）定子鐵心附加損耗計算如下。定子齒部附加損耗為 13.413-6.502=6.911 kW ；定子軛部附加損耗為 28.583-20.187=8.396 kW。3） 轉子鐵心附加損耗計算如下。轉子齒部附加損耗為 1.328-0.364=0.964 kW；轉子軛部附加損耗為2.427-0.889=1.538 kW。

繼續對定、轉子繞組中的附加損耗進行分離。定子繞組中附加損耗采用解析法評估即可滿足工程設計要求，該方案

定子繞組的電阻增加系數如公式（11）所示。

定子繞組附加損耗如公式（12）所示。

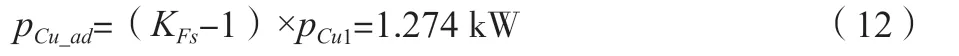
轉子繞組采用有限元計算其交流損耗，額定狀態下轉子繞組歐姆損耗分布如圖 5 所示。

由圖 5 可知，轉子導條受磁力線透入的影響，渦流損耗分布位置主要集中在導條表面。在有效鐵心段內，轉子導條計算實體損耗為 22.53 kW。根據公式（3）計算有效鐵心長度內轉子線圈直流電阻與直流銅耗，如公式（13）～公式（14）所示。

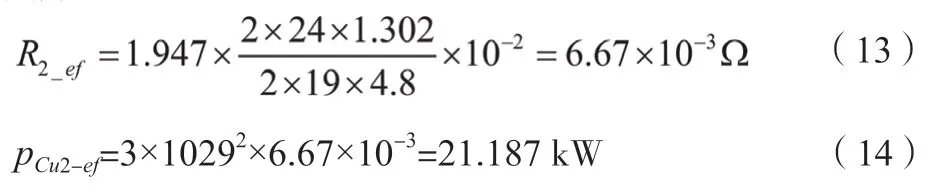
圖5 轉子導條歐姆損耗分布

轉子繞組槽內部分渦流損耗如公式（15）所示。

2.3 小結

至此，該款電機方案負載狀態下各部分附加損耗分離已經完成，各部分附加損耗值見表 7。該電機利用 IEC 標準計算其推薦附加損耗值為 41.2 kW。以上計算可準確分離出的附加損耗為 33.803 kW，該分離比例已經達到了 IEC 標準推薦值的 82%。這說明采用該方法可以準確分離絕大部分的附加損耗，為后續溫升計算提供更準確的依據。另外，剩余18% 的附加損耗可能集中在端部金屬部件與鐵心周圍的結構件中[7]，這一部分損耗的施加位置及施加比例需要進一步根據溫升反饋結果進行校正。

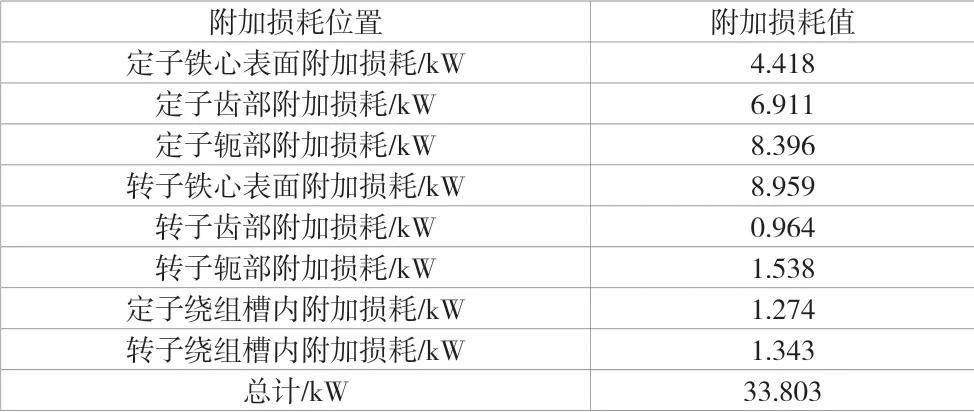
表7 各部分附加損耗值匯總

3 結語

該文對兆瓦級雙饋風力發電機負載附加損耗進行計算與分離，在原理層面闡述了分離的基本原則與計算方法，并結合某款 7 MW-10.5 kV 高壓雙饋風力發電機設計案例進行分析。采用解析—有限元相結合的方法可以準確分離絕大部分的附加損耗，為后續溫升評估與計算提供相對準確的依據，也為相同類型的電機設計提供一定參考。