積累基本活動經驗的圖形與幾何教學策略研究*

孫新宇 吳秀君，2，T 郭夢媛 葉舒琪

（1.江漢大學人工智能學院，武漢，430056；2.江漢大學武漢研究院，武漢，430056）

根據國內外關于活動經驗的文獻和教育理論，不難發現人們都十分贊同“活動促進學習”“從做中學”的觀點，重視新經驗與舊經驗的聯結[1-6]。但大部分實踐研究都只注重教師的活動教案設計和學生參與方面，真正運用在活動教學過程與實踐操作中的研究不夠完善，提出的教學建議比較零散，缺少系統性，教師在真正教學實踐時難以把握。針對上述情況，我們將基于數學活動經驗的視角，進行初中圖形與幾何的教學策略研究。

2021 年9 月至2021 年12 月，我們在武漢市某初中對學生進行問卷調查和對數學教師進行訪談，了解基于數學活動經驗的初中圖形與幾何教學現狀。然后，在該初中進行為期四個月的課堂觀察，依據建構主義學習理論、杜威的經驗主義理論、弗賴登塔爾的數學教育理論和奧蘇泊爾的認知同化學習理論提出相應教學策略，然后在兩個教學班進行教學實踐與策略修正。初中階段是學生開始從形象思維向著抽象思維發展、轉變的時期，圖形與幾何的計算、演繹推理復雜度不斷躍升，對于大部分學生還是有很大的挑戰性的。同時圖形與幾何這一部分無論計算還是證明，都需要嚴格的寫作規范與依據，是培養學生嚴謹性和規范性的重要時期。下面結合自身課堂觀察，在實踐中積累的案例和優質課案例庫研讀對數學活動經驗視角下的初中圖形與幾何教學策略。

一、設置合適的導入方式，喚醒學生的原始經驗

從學生問卷結果可以看出，絕大多數學生在學習圖形與幾何新內容時會借助以往的知識經驗，因此教師在進行新的圖形與幾何內容教學前，需要了解學生具備哪些原始經驗，去設置能夠喚醒學生原始經驗的情境導入。教師可根據具體內容設置新知引入的類型，大部分教師會選擇創設生活情境引入新知和復習舊知引入新知兩種類型。

創設生活情境引入新知這種類型，非常適合與日常生活相貼近的數學知識，這樣的教學設計能夠引起學生的共鳴，從而激發學生繼續學習探索的興趣，培養學生的情感性經驗。比如在黃金矩形教學中從觀察收集美麗的矩形物品導入。又如，在探索軸對稱的性質時，教師可以創設能引起學生動手、觀察和思考的生活情境。活動一：觀察屏幕中自然景觀、建筑物以及日常生活用品的圖片，它們有什么共同特點。活動二：把紙對折，在折痕不被完全剪斷的情況下剪出一個圖案。通過動手操作、觀察這樣的活動，讓學生體驗軸對稱圖形的特點以及在生活中的應用，積累動作性經驗和觀察性經驗。

復習舊知引入新知的類型適合前后知識聯結性強的教學內容。比如在探究平行線的性質時，教師通過提問“上節課學習的平行線三種判定方法的條件、結論分別是什么？如果把判定方法的結論和條件反過來，還成立嗎？”來引入探究課題，有意識地讓學生回顧前面學習的知識，通過類比研究平行線判定的過程去研究平行線的性質，積累學生歸納、類比的抽象性活動經驗。如果教學時間不夠，導入環節可以提前到課外進行，提前喚醒學生需要的原始經驗。

二、設計實踐和探究性的數學活動，留給學生充足的參與時間

根據學生問卷顯示，雖然只有58%的教師會布置探究性的作業，但大部分學生愿意去完成探究性的作業，因此教師應該在圖形與幾何的教學中有意識地多設計實踐性和探究性的數學活動，并在進度安排上留出足夠的時間給學生進行動手操作、觀察、思考、探究、歸納和表達，至于課堂探索時間與進度的沖突問題，可以借助線上平臺在線上或者課下的前置性活動進行預備，縮短課堂上的探索時間。

實踐和探究性的數學活動能有效調動學生的求知欲，激發學生學習積極性，在問題探究中獲得推理能力的提升，體會獲得知識的愉悅，增強學習數學的信心，有效改善學生推理能力不足的現狀，有效促進學生情感性經驗、動作性經驗、觀察性經驗和抽象性經驗的積累。比如，教師通過設計“平行線分線段成比例”“平行線分線段成比例在相似三角形的應用”“相似三角形的判定”“相似三角形判定的變式應用”的數學活動引導學生在做數學活動中對知識經驗一步步深化吸收，最終實現“相似三角形”新知在原有“三角形”與“相似圖形”認知結構中的同化，積累數學活動經驗。

又如，在探索等腰三角形的性質時，教師設計如下活動：（1）按教材給出的方式剪出等腰三角形；（2）觀察剪出的等腰三角形紙片，概括剪出的等腰三角形的特征；（3）觀察其他同學剪出的等腰三角形，是否都具有上述概括的特征；（4）在練習本上任意畫出一個等腰三角形，剪下來折一折，是否符合前面概括的特征。由此概括出等腰三角形的性質，其中活動一是實踐性數學活動，活動二和活動三屬于探究性數學活動，活動四是實踐與探究相結合的活動。整體活動安排為學生先對一個等腰三角形研究發現其特征，然后在對其他等腰三角形進行研究發現特征的一致性，從而概括出等腰三角形的形式，在折疊、觀察、思考和討論的過程中充分體驗特殊到一般的歸納方法，積累學生的思維性經驗。

三、采用問題引導的教學方法，培養學生的抽象性經驗

抽象性經驗主要有猜想、思考、歸納、推理、表達。通過學生問卷和教師訪談顯示，學生的表達、歸納和推理等能力不足，教師在課堂中未能在思考探究環節留給學生充足的時間，當學生難以解決問題時，部分教師會直接給出結論從而導致學生的表達、歸納和推理等抽象性經驗積累不足，不利于發展學生的問題解決能力。教師在數學教學活動中要做引領者，當學生難以進行數學活動的任務時，要及時設置問題串，打破學生與問題間的隔閡，引導學生在一步步、循序漸進解決問題的過程中，經歷知識的再發現、再創造，感受數學魅力，獲得探索的樂趣和成就感，培養情感性經驗和分析、歸納、推理、反思等抽象性數學經驗。比如學生理解不了黃金矩形第三步的折疊方式時，依據再創造理論，教師用展示和提問的方式引導、幫助這部分學生去思考理解，進而實現“黃金矩形”的再創造，也為后續黃金矩形的驗證提供了思路，有效積累了學生動作性經驗和思考、推理的抽象性經驗。

又如，在探索圓周角定理時，教師讓學生測量同一圓弧所對的圓心角和圓周角的度數，并回答以下問題：這兩個角有怎樣的關系？繼續在圓上任取一條圓弧，再次測量這條弧所對的圓心角和圓周角的度數，你還能得出同樣的結論嗎？學生在教師一步步提問和參與活動中發現結論，積累了猜想、分析等抽象性經驗。

四、借助數學軟件，讓學生在觀察和操作中發展空間想象和幾何直觀

圖形的變化一直是圖形與幾何教學中的難點，由于學生缺乏對圖形變化軌跡的空間想象，所以僅僅依靠教師的講解難以理解和解決問題。通過教師訪談，了解到不少數學教師在講解圖形與幾何時，會利用幾何畫板等將圖形變化變得直觀化的數學軟件幫助學生想象、理解，特別是在新授課的探究環節和習題課的講解環節。

在學生猜想的基礎上，教師利用幾何畫板的直觀性和準確性，幫助學生加深對平行線分線段成比例的理解和記憶，發展學生的空間想象和幾何直觀。習題是考察學生對“圖形的變化”掌握情況的有效途徑之一，特別是圖形與幾何中的動點問題，很多學生因為想象不出圖形的運動軌跡導致問題未能解決。例如，等腰△ABC中，∠BAC=120°，AB=AC=，點D在邊BC上，CD=2，將CD繞點C逆時針旋轉α°到CE，連接AE，以AE、AB為邊做平行四邊形ABFE，連DF，求DF最大值。教師在講解這個動點問題前，通過詢問了解到有超過一半的學生不會做的原因是想象不出來F點的運動軌跡，只要明確了F點的運動軌跡，就可以根據三角形的三邊關系找到DF的最大值，所以解題的關鍵點在于明確F點的運動軌跡。學生大部分能想象和發現E點的運動軌跡是個圓，還有少部分能理解F點的運動是跟隨E點變化的，但想象理解不了F點的運動軌跡和E點的運動軌跡在形狀、大小上是一樣的，所以教師借助幾何畫板，拖動E點，學生在觀察幾何畫板中E點和F點的軌跡變化過程中，培養他們的空間想象和幾何直觀，積累思維性經驗。

五、引導學生歸納小結，教師課后進行教學反思

根據學生問卷結果顯示，有64%的學生很少會在學習活動后進行歸納，甚至從來不會歸納，這也能說明有64%的學生不能很好解決問題的原因，因此教師應該注重對學生歸納能力的培養，進而提高學生的問題解決能力。歸納小結存在于教學活動中的知識點小結和課堂內容小結，小結環節不僅可以幫助學生梳理知識結構，將新的活動經驗融入到原有經驗結構中，還可以從學生給出的反饋看出本堂課教學目標達成的大致情況，但具體目標完成情況還需要結合習題、作業的完成情況來分析。這些做法有利于教師對自己的教學進行反思，發現教學中存在的問題，從而使得后續的教學更加完善。

例如，在教師講解角的概念后，以做答題游戲的形式促進學生對角的概念的認識歸納，培養學生的問題解決能力，從答題的速度和準確率檢驗學生對角的概念教學目標的掌握情況，及時調整教學進度。此外，做游戲的形式能極大提高學生數學學習的興趣和主動性，有利于推進后面的教學環節。

課堂結束后，教師也應該引導學生對本節課所有的知識點進行歸納小結，將學到的新知識經驗及時梳理構建知識框架，促進知識經驗的吸收。如在講解完角的比較與運算后，教師引導學生回顧本節課的主要內容，構建知識與方法的框架（如圖1），完善學生的認知結構。

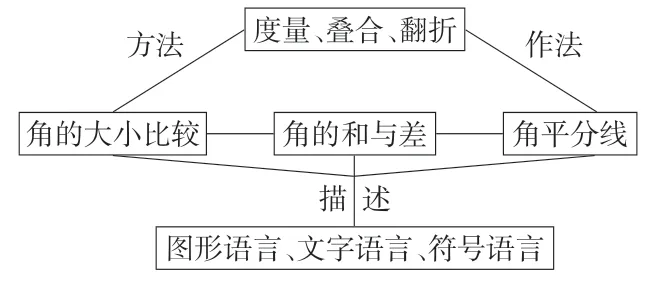
圖1 知識框架圖

六、利用線上平臺和工具，合理安排數學活動流程

教師訪談結果顯示，教師在課堂上未能留給學生充足的時間思考探究，因此教師應該合理安排教學流程，利用線上平臺增加課外實踐應用的環節，使學生能在數學活動中充分體驗探索數學的樂趣，積累數學活動經驗。

課前教師可以將活動預案通過PPT 或者小視頻的方式發布到班級線上平臺，如QQ 課堂、雨課堂、教育云等互動交流平臺，讓學生在課前提前理解活動的要求與內容，留足時間、動員家庭成員一起完成活動預案，為課上的新知探究環節預備好需要的原始經驗。如課前“收集好看的矩形”活動任務的布置，不但能夠使得學生在完成課前活動任務的過程中喚醒原始經驗，還能夠在課堂上留給學生更多的時間去思考探究，積累數學活動經驗。

課后學生可以以小組形式進行網上討論并推舉小組最佳作品參加網上作品展示與互評，增加作品的反饋環節，加強學生互助合作與情感交流，這樣有利于增加集體榮譽感。