基于代理模型的液壓螺栓拉伸器優(yōu)化設計

陳國炎， 錢亞平， 胡 鶯， 石茂林

(1.江蘇理工學院 機械工程學院， 江蘇 常州 213001； 2.常州愛普超高壓液壓系統(tǒng)有限公司， 江蘇 常州 213001；3.江蘇大學 農(nóng)業(yè)工程學院， 江蘇 鎮(zhèn)江 212013)

引言

中、大型螺栓連接在核電、火電、風電設備裝配中起到至關重要的作用。增加螺紋預緊力是保證螺栓連接質(zhì)量的重要手段，與用榔頭敲擊、力矩扳手等傳統(tǒng)技術手段相比，液壓螺栓拉伸器具有預緊力可控、螺栓受力均勻、損傷小等優(yōu)點[1]。隨著液壓螺栓拉伸器的廣泛應用，對其提出的要求越來越多。例如，在高空、狹小空間中使用時，對液壓螺栓拉伸器體積、重量有著嚴格要求。當結構設計不合理時，活塞等關鍵部件容易發(fā)生局部應力過大，導致彎曲變形及油缸爆裂，給企業(yè)造成嚴重損失[2-3]。

目前，關于液壓螺栓拉伸器的研究較少，多集中于原理介紹、強度校核，少部分研究涉及結構優(yōu)化，但未給出具體優(yōu)化過程。例如，文獻[4]分析了液壓螺栓拉伸器的工作原理，結合作者在海洋石油工程中的應用經(jīng)驗，提出了油壓計算、分布加壓、次序預緊的作業(yè)建議，改善了法蘭多個螺栓的預緊力分布；文獻[5]總結分析了液壓螺栓拉伸器主流產(chǎn)品的螺栓上緊程序、油壓加壓程序的不同，比較了國內(nèi)外常用的預緊力計算方法，并結合個人使用經(jīng)驗給出了建議；文獻[6]采用有限元法對拉伸器的關鍵結構進行了強度校核，檢驗了結構的安全性和可靠性；文獻[7-8]建立了缸體、螺帽的有限元模型，通過優(yōu)化缸體的若干設計參數(shù)，降低了缸體應力，但僅給出了優(yōu)化結果，未給出具體優(yōu)化過程。可以看出，關于液壓螺栓拉伸器優(yōu)化設計研究較少，少部分優(yōu)化研究也未給出詳細的優(yōu)化過程及方法。因此，提出面向液壓螺栓拉伸器的優(yōu)化設計方法就成為亟需解決的問題。

從以上研究中可以看出，傳統(tǒng)結構優(yōu)化問題主要通過有限元仿真進行。隨著計算機技術的迅猛發(fā)展，有限元模型的靜力學仿真精度得到大幅提升，但相應的計算成本也顯著增加，單次仿真耗時過長，而優(yōu)化過程往往需要成百上千次調(diào)用仿真模型，最終導致基于仿真的結構優(yōu)化計算成本難以忍受甚至無法實現(xiàn)。為了解決這一問題，研究人員提出了代理模型，通過有限個樣本點的數(shù)值仿真結果，利用核函數(shù)等方法建立設計變量與輸出響應的數(shù)學模型，從而近似替代仿真模型，大幅降低了計算成本，提升了計算效率[9-10]。例如，文獻[11]采用代理模型替代機械式挖掘機動臂的靜力學有限元模型，對動臂的設計變量進行了優(yōu)化。文獻[12]采用代理模型替代某型閥門的計算流體力學有限元模型，揭示了代理模型用于替代高計算成本流體計算仿真的可行性。文獻[13]使用離散元方法建立壩基注漿仿真模型，基于仿真數(shù)據(jù)建立代理模型，用于注漿量的預測與優(yōu)化。文獻[14]采用代理模型替代擠壓鑄造過程的熱 - 力數(shù)值仿真模型，并用于評價和計算擠壓鑄造機的可靠性分析。更多關于代理模型工程應用的文獻可參考文獻[15]。為此，本研究提出基于代理模型的液壓螺栓拉伸器優(yōu)化設計方法，以THDG039型號高壓液壓拉伸器為對象，利用SolidWorks與ANSYS軟件構建下活塞參數(shù)化模型并進行靜力學分析，基于代理模型在滿足體積約束下優(yōu)化最大應力。所提出的優(yōu)化方法可為企業(yè)研制系列高壓液壓拉伸器提供技術支持。

1 液壓拉伸器下活塞有限元模型

以常州某公司THDG039型號高壓液壓拉伸器為對象(圖1)，采用SolidWorks建立拉伸器下活塞三維模型并導入ANSYS進行靜力學分析。下活塞材料為45CrNiMo，密度7850 kg/m3，彈性模量2.06×105MPa，泊松比為0.30。網(wǎng)格劃分采用ANSYS自帶網(wǎng)格劃分，對容易發(fā)生應力集中及最大應力出現(xiàn)部位進行局部加密，生成網(wǎng)格2091676，節(jié)點2861530。分析場景設定為螺栓拉伸穩(wěn)定、不發(fā)生位移變動、上下活塞不發(fā)生相對運動的情況，下活塞主要載荷為液壓面承受的液壓油軸向壓力，與缸體接觸面添加橫向、前后約束，與螺栓接觸面位移設定為0。采用個人臺式機進行計算(CPU：Intel Core i7-10700KF，3.8 GHz；RAM：32 GB)，單次計算時間約13 min，計算結果如圖2所示，選用Von-mise應力作為應力指標，最大值為576.03 MPa，出現(xiàn)在上第二端面與外軸立面之間的銜接處。

圖1 液壓拉伸器Fig.1 Hydraulic bolt tensioner

圖2 有限元分析結果Fig.2 Results of finite element analysis

2 代理模型建立與誤差分析

代理模型是基于少量數(shù)值仿真數(shù)據(jù)建立的描述設計變量與輸出響應關聯(lián)關系的數(shù)學模型，其建立過程主要包括5個步驟：①設計變量和優(yōu)化目標確定；②試驗方案設計；③仿真/實驗結果獲取；④模型建立；⑤精度驗證，如圖3所示。

圖3 代理模型構建流程Fig.3 Construction of surrogate models

圖4 下活塞設計變量Fig.4 Design variables of down piston

2.1 試驗設計

本研究選擇下活塞最大應力與體積作為優(yōu)化目標，選用其4個結構設計參數(shù)作為設計變量，如圖4所示，每個設計變量取值范圍為初始設計值上下浮動0.5 mm，最終獲得設計變量的變動范圍如表1所示。在設計過程中，零件尺寸在整體尺寸鏈不變情況下，隨設計變量改變而發(fā)生變動。

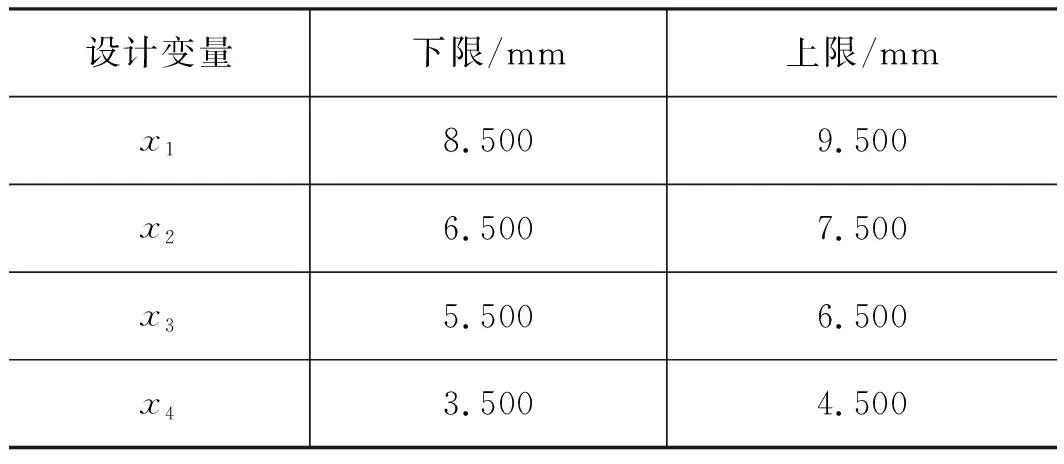
表1 設計變量取值范圍Tab.1 Ranges of design variables

試驗設計(Design of Experiments, DOE)發(fā)源于統(tǒng)計學，目的在于如何通過合理的數(shù)據(jù)采樣獲取樣本空間內(nèi)設計變量與輸出響應的關聯(lián)信息。對于代理模型而言，合理的試驗設計選點能夠有效提升模型精度，常用的試驗設計方法有正交試驗設計、拉丁超立方試驗設計、全析因試驗設計方法等[16]。本研究采用拉丁超立方法進行抽樣，其可在保證采樣點均勻分布的同時，最大程度獲取樣本空間信息。基于代理模型應用經(jīng)驗，訓練樣本容量設定為20(5倍于設計變量)，對應的空間分布如圖5所示。可以看出，生成樣本均勻布滿整個樣本空間，能夠有效獲取樣本空間中設計變量與輸出響應的關聯(lián)信息。

2.2 模型構建與誤差分析

近年來，研究人員提出了眾多代理模型，例如多項式回歸(Polynomial Response Surface，PRS)、徑向基函數(shù)(Radial Basis Function，RBF)、克里金法(Kriging Method，KRG)、支持向量回歸(Support Vector Regression，SVR)。這些方法按照訓練點預測值與真實值相同與否，分為回歸方法與插值方法。其中，支持向量回歸與克里金法分別為回歸方法與插值方法的代表。從既有文獻中可知，沒有任何一種代理模型能夠在所有問題中獲得最好的性能表現(xiàn)，因此需要對模型進行檢驗，選擇出最好的代理模型[17-18]。本研究選用RRS，RBF，KRG與SVR共4種代理模型，介紹如下：

1) 多項式回歸

多項式回歸的基本形式表示如下：

y=f(x)+ε

(1)

式中，y—— 模型的輸出變量

x=(x1,x2,…,xd) —— 模型的輸入變量，其中d為輸入變量數(shù)量

f(x) —— 多項式方程

ε—— 隨機誤差

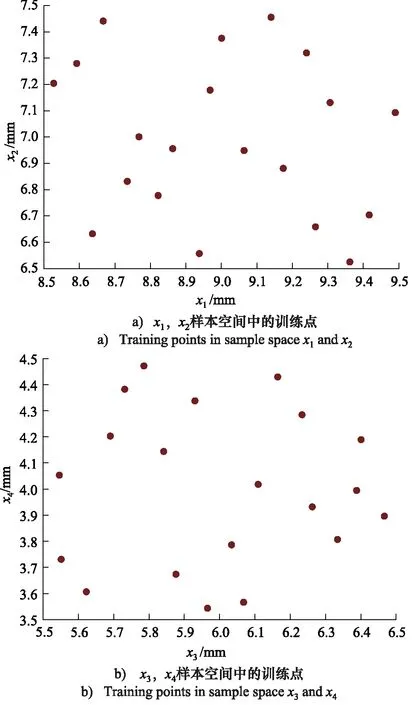
圖5 樣本空間中的訓練點Fig.5 Training points in sample space

f(x)通常采用二階多項式，如下所示：

(2)

利用最小二乘法，多項式系數(shù)a0，ai，aii和aij可通過如下公式獲得：

a=[X′X]-1XY

(3)

式中，a—— 多項式系數(shù)組成的向量

X—— 輸入變量矩陣

Y—— 輸出變量矩陣

2) 徑向基函數(shù)

徑向函數(shù)是指以預測點與訓練點之間的距離為自變量的函數(shù)[19]。以徑向函數(shù)為基函數(shù)，通過線性疊加構造出來的代理模型即為徑向基函數(shù)代理模型。基本思想是以訓練樣本為中心，通過徑向函數(shù)的線性疊加來計算待預測點xnew的輸出值，如下所示：

(4)

式中，ωi—— 徑向函數(shù)系數(shù)

n—— 訓練點數(shù)量

Φ(ri) —— 徑向函數(shù)

(5)

在滿足訓練點不重合條件下，且函數(shù)Φ(ri)為正定核函數(shù)，方程：

ωT=Φ-1·Y

(6)

存在唯一解，最終預測點的輸出可通過式(4)獲得。

3) 克里金法

克里金法假設輸入變量x和輸出變量y滿足如下關系[20]：

(7)

式中，fj(x) —— 基函數(shù)

p—— 基函數(shù)數(shù)量

βj—— 基函數(shù)系數(shù)

Z(x) —— 高斯過程，滿足如下條件：

E(Z(x))=0

(8)

E(Z(xi)Z(xj))=σ2R(θ,xi,xj)

(9)

σ2—— 樣本方差

R(θ,xi,xj) —— 相關矩陣

θ—— 相關矩陣的參數(shù)向量

記：

(10)

得輸出向量：

Y=Fβ+Z

(11)

式中，Z=(Z(x1),Z(x2),…,Z(xn))T。由線性無偏條件和拉格朗日乘子法，得到輸入x的輸出值和基函數(shù)系數(shù)最優(yōu)估計如下：

(12)

(13)

待預測樣本xnew的輸出值如下所示：

(14)

4) 支持向量回歸

支持向量回歸的基本形式可表述如下：

y=ωT·φ(x)+b

(15)

式中，φ(x) —— 輸入x向高維空間的映射

ω—— 權重向量

b—— 線性方程的偏置項

在支持向量回歸中，通過優(yōu)化如下?lián)p失函數(shù)：

(16)

獲取式(15)中的最優(yōu)參數(shù)。損失函數(shù)C的前半部分為權重向量ω的正則化項，決定模型的泛化能力；后半部分為所有訓練數(shù)據(jù)的回歸誤差，決定模型的訓練精度；參數(shù)γ決定模型的泛化能力與訓練精度的平衡關系。構建如下拉格朗日函數(shù)：

b+ei-yi}

(17)

式中，αi為拉格朗日乘子。對式(17)中各項求偏導，可得權重向量ω為：

(18)

因此，式(15)可改寫為：

(19)

預測點xnew的輸出為：

(20)

φ(xi)可構成如下正定核函數(shù)：

K(xi,xj)=φ(xi)Tφ(xj)

(21)

通過求解如下線性方程組獲得α和b：

(22)

結果如下：

(23)

2.3 誤差分析

本研究選用的代理模型基本參數(shù)如表2所示。

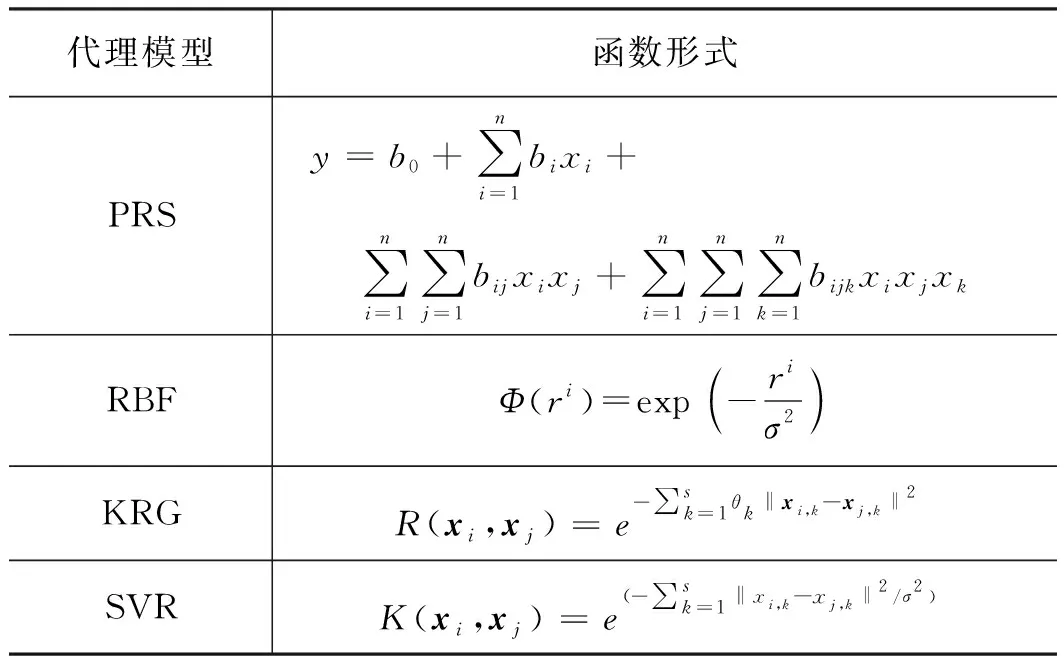
表2 代理模型參數(shù)與函數(shù)形式Tab.2 Parameters and functions of surrogate models

生成20個測試點檢驗代理模型精度，并通過如下3種指標進行評價，包括全局誤差指標決定系數(shù)R方(R2)與均方根誤差(RMSE)，局部誤差指標最大絕對誤差(MAE)，公式如下所示：

(24)

(25)

(26)

表3 4種代理模型檢驗精度對比Tab.3 Performance comparison of four surrogate models

進一步對KRG和SVR預測結果進行分析，可以看出兩種代理模型對于體積的預測精度都非常高，R2接近于1。對于最大應力，KRG代理模型精度要遠好于SVR。一般而言，當R2大于0.8時，就可以認為代理模型精度能夠滿足要求，用于替代原始模型。在本研究測試的4種代理模型中，KRG代理模型在R2，RMSE，MAE中對體積和最大應力2個預測目標均取得最優(yōu)，預測值與真實值較為接近，如圖6所示。R2分別為0.987和0.855，因此KRG代理模型被用于后續(xù)優(yōu)化分析。統(tǒng)計20個測試點的代理模型和有限元仿真的平均計算時間，所得結果如表4所示。從表中可以看出，4種代理模型的計算成本顯著低于有限元仿真模型，能夠節(jié)省大量的計算成本，揭示了代理模型在液壓螺栓拉伸器優(yōu)化設計中的優(yōu)越性。

表4 代理模型與有限元仿真時間對比Tab.4 Time comparison between surrogate models and finite element simulation

圖6 KRG代理模型預測結果Fig.6 Prediction results of KRG surrogate model

3 優(yōu)化結果

基于所建立的KRG代理模型對下活塞進行優(yōu)化設計。在下活塞優(yōu)化過程中，最大應力作為優(yōu)化目標；約束條件主要由最大應力與體積約束組成，下活塞材料為40CrNiMo，安全系數(shù)為1.3，屈服點σs為785 MPa，則最大許用應力為603.85 MPa；體積最大為初始體積的2%，即64171.0 mm3。優(yōu)化問題定義如下：

minmize[σmax]

Subject to

8.500 mm≤x1≤9.500 mm

6.500 mm≤x2≤7.500 mm

5.500 mm≤x3≤6.500 mm

3.500 mm≤x4≤4.500 mm

σmax≤603.85 MPa

V≤64171.0 mm3

選用MATLAB中fminimax函數(shù)求解上述優(yōu)化問題，結果如表5所示。進一步檢驗代理模型優(yōu)化結果，基于優(yōu)化設計變量繪制下活塞三維模型，導入有限元軟件進行靜力學分析仿真，結果如圖7所示。將代理模型優(yōu)化結果、初始與優(yōu)化設計仿真結果列于表6。可以看出，最大應力經(jīng)優(yōu)化后降低5.61%，為574.73 MPa，誤差為1.82%；體積上升2.52%， 突破設定閾值2%，發(fā)生這一現(xiàn)象的主要原因是代理模型自身的誤差(代理模型預測值未突破約束，為64169.6 mm3)。由此可見，雖然代理模型存在一定預測誤差，但仍可獲得較為理想的優(yōu)化結果，證明了代理模型在液壓螺栓拉伸器優(yōu)化中的可用性。

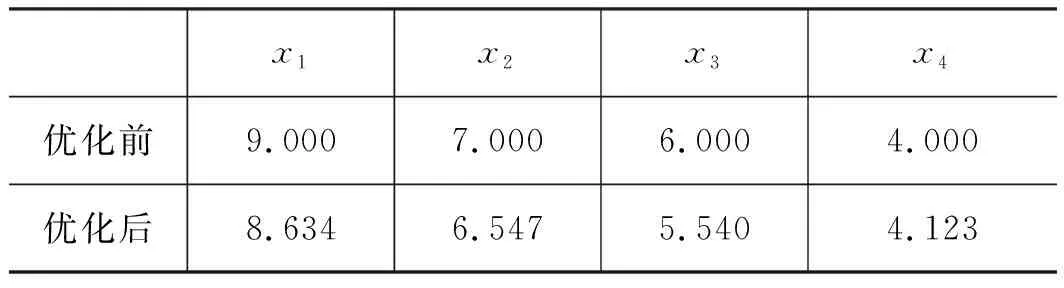
表5 優(yōu)化結果Tab.5 Optimization results mm

表6 初始與優(yōu)化設計對比Tab.6 Comparison between initial and optimal design variables

圖7 優(yōu)化設計變量的仿真結果Fig.7 Simulation results of optimal design variables

4 結論

以液壓螺栓拉伸器中的下活塞為研究對象，采用SolidWorks和ANSYS軟件對下活塞進行參數(shù)化建模與有限元仿真，基于代理模型對最大應力進行優(yōu)化。采用拉丁超立方法生成20個訓練點，利用多項式回歸、徑向基函數(shù)、克里金法、支持向量回歸分別建立代理模型，通過20個測試點檢驗模型精度，結果表明克里金法具有較好的預測精度，在優(yōu)化過程中用于替代仿真模型。優(yōu)化結果表明，在體積增大2.52%情況下，最大應力降低5.61%，體積和最大應力優(yōu)化結果預測誤差分別為0.52%和1.82%。本研究工作揭示了代理模型在液壓螺栓拉伸器優(yōu)化設計中的可用性與可行性。