頻域組稀疏滾動軸承特征提取方法

王華慶 劉澤源 盧威 宋瀏陽 韓長坤

摘要：針對時域非平穩振動信號模式混疊、信噪比低，以及傳統稀疏表示算法模型復雜、優化求解算法難以確定，導致故障特征提取難的問題，提出了頻域組稀疏和群橋約束改進迭代收縮閾值優化的故障特征提取方法（Group Sparse Representation in Frequency Domain，GSRF）。將振動信號轉換至頻域并對變量分組，構造施加群橋約束的最小二乘回歸模型，準確篩選沖擊相關變量；引入迭代重加權系數簡化方程，以軟閾值收縮優化求解頻域稀疏信號；對重構的時域稀疏信號進行包絡頻譜分析提取故障特征。試驗結果表明，提出的頻域組稀疏算法優于傳統的結合 L21范數約束的組稀疏索套方法，可有效提取微弱故障特征，實現稀疏域下的軸承故障診斷。

關鍵詞：故障診斷；滾動軸承；微弱故障；稀疏表示；特征提取

中圖分類號： TH165+.3；TH133.33??? 文獻標志碼： A??? 文章編號：1004-4523（2022）05-1242-08

DOI：10.16385/j .cnki .issn .1004-4523.2022.05.022

引言

滾動軸承廣泛應用在石化、軍工等領域，作為機械設備的重要傳動零件，軸承在高速重載的工況下容易發生損傷失效，影響設備正常運轉，因此對軸承早期故障的監測和診斷至關重要[1]。分析振動信號以提取故障特征是常用的診斷方法[2] ，但惡劣工況和復雜傳動系統往往使測得的振動信號呈現非高斯非平穩、模式混疊、信噪比低的特性，故障特征被噪聲淹沒[3]。因此從早期微弱軸承故障信號中提取特征信息具有重要意義。

稀疏表示在故障診斷方向應用廣泛，求解過程可以大致分為確定數學模型和優化求解兩部分[4]。其數學模型是范數約束的最小二乘逼近函數，Hou 等[5]對希爾伯特解調信號施加 L1約束增強了分解結果的稀疏性，實現了未知轉速的軸承故障診斷。 Zheng 等[6]引入 L1、組2范數及無窮范數約束目標函數，在保證重構信號的稀疏性的同時提升了降噪效果，增強了早期微弱故障特征。優化求解算法可以大致分為貪婪算法、優化約束法、逼近算法、同倫算法。經典的貪婪算法包含由Mallat等提出的匹配追蹤（Matching Pursuit，MP）及由 Pati 等改進的正交匹配追蹤算法（Orthogonal? Matching? Pursuit， OMP），其重構信號往往是近似解[7?8]。優化約束法將原目標函數（不光滑或不可導等不易快速求解的問題）轉換為光滑的或可求導問題，優化后的目標函數和原目標函數不同，簡化了求解過程。其代表算法為梯度下降和交替方向乘子法（Alternating Direc? tion of Method of Multipliers，ADMM）[9]。逼近算法將非光滑約束問題拆解為多個簡單子問題，利用逼近算子分別求解這些子問題以提高求解效率。經典算法包括收縮算子、增廣拉格朗日算法、受控極小化（Majorization Minimization，MM）、迭代收縮閾值算法（Iterative? Shrinkage ? Thresholding? Algorithm ， ISTA）等[10?12]。

組稀疏回歸模型在求解中協同約束組內、組間變量，促進分解的稀疏性。An 等[13]提出多尺度周期組索套，利用多級小波子帶構建稀疏模型，通過 MM 優化非凸罰函數，在小波域提取周期脈沖，實現強噪干擾下的特征提取。Zhao 等[14]構建稀疏多周期組套索模型，使用 MM 解耦多重故障，實現了低信噪比復合故障信號的診斷。Zhao 等[15]基于增強稀疏組 Lasso 懲罰，自適應選擇確定參數，并在 MM 優化中嵌入周期先驗，直接提取時域脈沖，實現了微弱故障信號的診斷。

雖然上述方法成功提取了故障特征，但仍存在如下問題。1）模型過于復雜，多數模型為提升分解結果會引入多項罰參量，容易降低組內、組間變量選擇的一致性。2）優化保凸能力弱，復雜非凸模型求解對優化算法要求高，當懲罰項不易平滑時將顯著增加計算復雜度。

為解決上述問題，提出了基于頻域的組稀疏特征提取方法，以組稀疏保證分解稀疏性的同時保留脈沖相關信息。軸承故障信號是故障特征信號與噪聲的耦合信號，時域降噪難以實現解耦，將信號變換到傅里葉正交空間，有利于實現信號解耦，降低噪聲，提取沖擊信號。因此，先建立沖擊敏感的數學模型并轉換至頻域的振動信號按組劃分，再對分組后的頻域信號施加群橋約束以選取沖擊相關特征變量，引入迭代重加權系數，簡化目標函數方程便于 ISTA 優化求解，最后重構稀疏時域信號，在包絡譜上提取出信號故障特征。 GSRF 對同一懲罰項施加多種約束來保證變量篩選的一致性和稀疏性，利用權重系數凸優化回歸模型，降低運算難度，通過對軸承早期故障信號的分析驗證了所提方法的有效性。

1 基本原理

1.1 稀疏表示

用于生物信息、數理統計、信號處理等領域的數據維數通常很大，對信號做稀疏表示有利于緩解數據的存儲、傳輸、提取的壓力。稀疏表示簡單理解為原信號是用少量基原子線性組合而成的[16]，即：

式中振動信號 Y ∈ Rn，觀測矩陣 D∈ Rn × m 可為字典集或變換矩陣，稀疏系數 a ∈ Rm，噪聲ε∈ Rn。

常用的稀疏表示模型可以總結為：

式中 p >0，懲罰系數λ>0。式（2）表示常用的范數約束求解，當 p=0時，是多項式復雜程度的非確定性問題，難以直接求解，Donoho與Candes等證明 p=1時，式（2）轉變為索套算法（Least absolute shrinkage and selection operator，Lasso ），在滿足一定稀疏性條件下，與p=0有同樣的稀疏解。

1.2 橋組稀疏

傳統 Lasso 算法僅能解決組內變量選擇問題，稀疏性不強，Yuan 等在 Lasso 基礎上引入組間變量選擇，Huang 等又加入了橋懲罰項，進一步提高了運算速度與稀疏性，廣泛應用在數據分析統計中[17?18]。

其原理為，對 n 維1列的信號 y =（y1，y2，…，yn ）′，有 n 維 d 列設計向量 Dk =（ D 1k，D 2k，…，Dnk ）′（k=1，…，d），A1，…，AJ 表示設計向量 D 的已知分組（1≤ J ≤ d），以aAj =（ak，k ∈Aj ）′表示第 j 組的回歸系數，有橋組稀疏目標函數為：

式中懲罰系數λ>0，橋懲罰系數γ>0。式（3）是非凸問題，需轉化為便于求解的凸函數。

1.3 迭代重加權

任意向量 e ∈ Rn，其p 范數可定義為：

對式（4）變形：

利用式（6）及權重 w 即可以將式（3）中的非凸問題轉變為凸優化求解[19]。

1.4 近端算子

有函數f（x ）=g（ x ）+h（x ），其中 g（ x ）是可導凸函數，h（x ）不可導，其最小值可由迭代循環求解：

式中? t 為步長，常取李普希茲常數的倒數；?g （ x ）為梯度。式（7）可寫為不動點迭代形式：

式中prox稱為近端算子，在廣義梯度下降更新求解中廣泛應用，下文將結合迭代重加權的思想進一步優化約束。綜上所述，確定了數學回歸模型和優化求解算法，便可通過迭代運算求近似解。

2 基于頻域組稀疏的特征提取

2.1 組稀疏

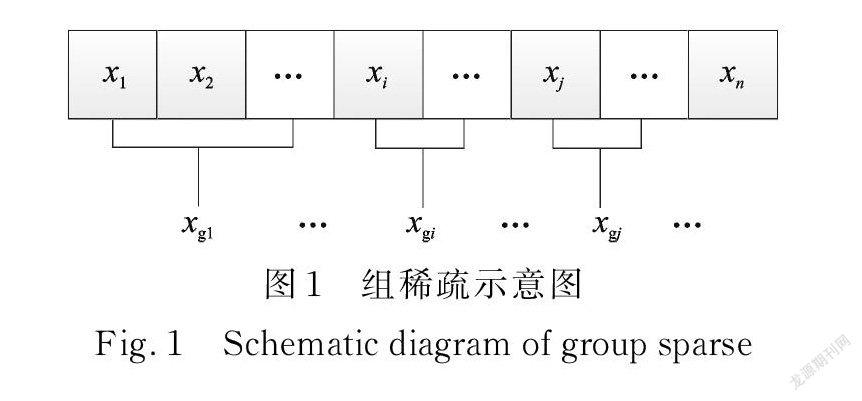
傳統稀疏約束對向量內全部變量進行篩選，沒有考慮變量間關系，組稀疏將 n 維向量 x 內變量分組，示意圖如圖1所示。

圖1中，xgi表示第i組變量，每組變量數量可以根據信號特點劃分，若不同組間無重復的變量可認為是非重疊組，反之認為是重疊組劃分，即當i≠j 時，非重疊組中xgi與xgj無相同元素，重疊組中xgi與xgj有相同元素。重疊組稀疏不僅約束組內變量，還影響組間變量的選擇，顯著增強每次迭代對沖擊相關變量的篩選能力，使重構時域信號具有更強的稀疏性[20]，沖擊特征更明顯。

為解決時域非平穩振動信號模式混疊、信噪比低及分解結果不稀疏的問題，將待處理信號轉換到頻域。引入重疊組稀疏后，數學回歸模型寫為：

式中 x 為待求解的稀疏信號，y 為轉換至頻域的原始振動信號，懲罰系數λ>0。2范數平方項保證重構信號和原信號的一致性，對組變量xg施加1范數約束以增強沖擊特征選取能力[21]。

2.2 組橋約束

為進一步提高分解結果的信噪比，引入群橋約束組的變量[22?23]，式（9）寫為：

式（3）中橋懲罰系數取0<γ<1時可以強化沖擊相關變量的選擇能力，此處依據經驗選取群橋系數γ=0.5，但式（10）是非凸優化問題，結合1.3節介紹的迭代重加權，式（10）轉化為：

上式形似式（2）的基礎 Lasso 問題。據1.4節介紹，式（12）的前一項可視為 g（ x ），后一項可視為 h（x ），對 g（ x ）二階泰勒展開并配方后，目標函數式（12）存在近端算子：

式（13）有數值解，更新可得稀疏信號 x。

2.3 基于頻域橋組稀疏的故障診斷方法

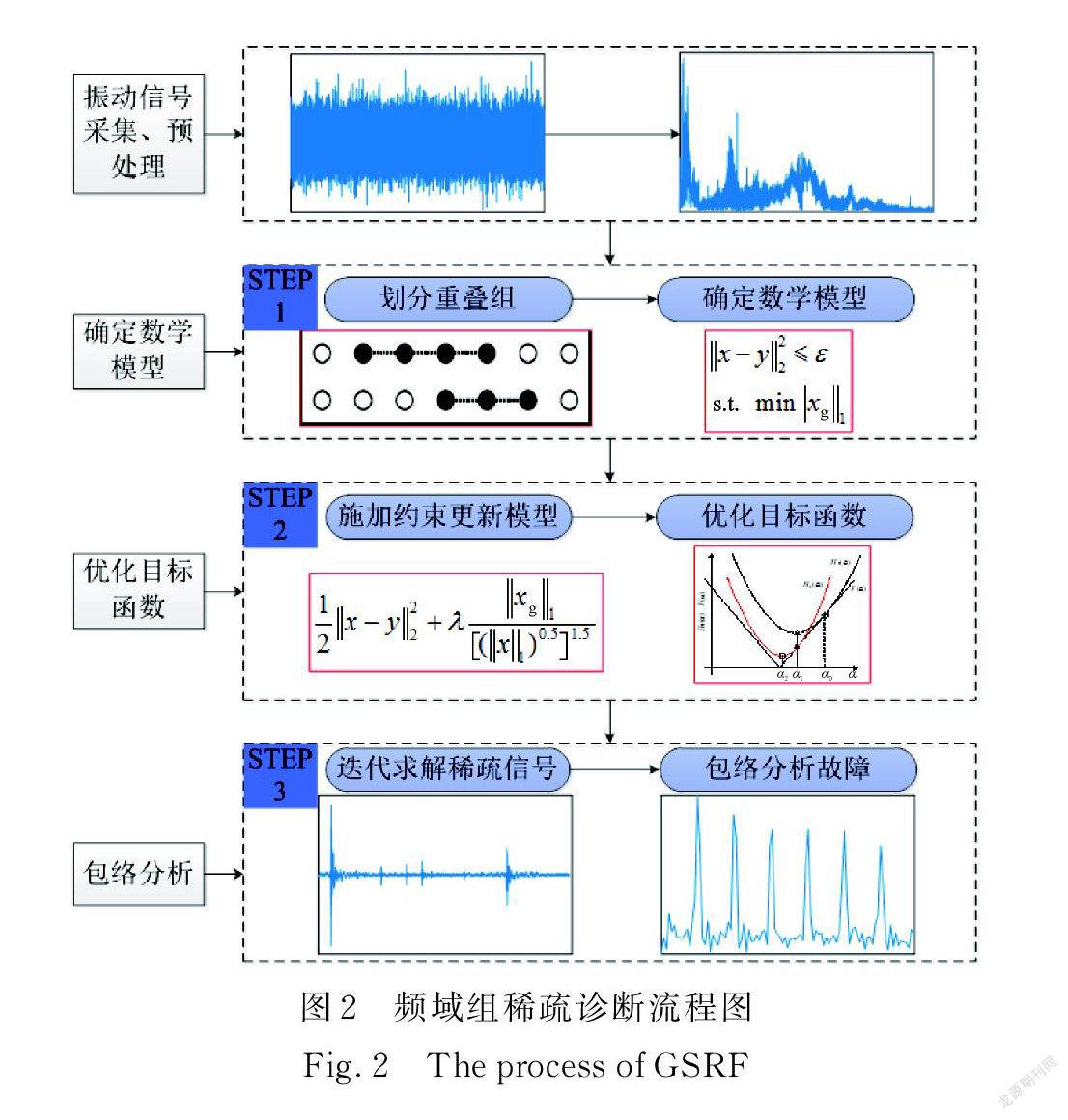
針對軸承的早期微弱故障，提出了以重疊組、群橋約束為基礎的稀疏模型，以迭代重加權和迭代收縮閾值為優化算法的微弱故障特征提取方法，其具體實現步驟如圖2所示流程圖。

所提方法為減弱非平穩時域噪聲干擾在頻域進行特征提取，主要步驟如下：

（1）對轉換到頻域的振動信號內的變量按照重疊組劃分，確定最小二乘結合 L1范數約束組變量的基礎數學模型。

（2）施加群橋約束，進一步強化篩選沖擊敏感的組間及組內變量，并引入迭代重加權系數簡化目標函數，將非凸問題轉化為形如加權 Lasso 的凸函數。

（3）對優化后的數學模型采用 ISTA 迭代更新求解頻域稀疏信號，再轉換回時域，最后對時域稀疏信號進行包絡譜分析，提取故障特征頻率，實現故障診斷。

3 實驗分析與驗證

為驗證 GSRF 的有效性，分別采用公開軸承故障數據及課題組試驗臺數據，與傳統非重疊組結合 L21范數約束的 Lasso 算法做了對比分析研究。

3.1 實驗驗證一

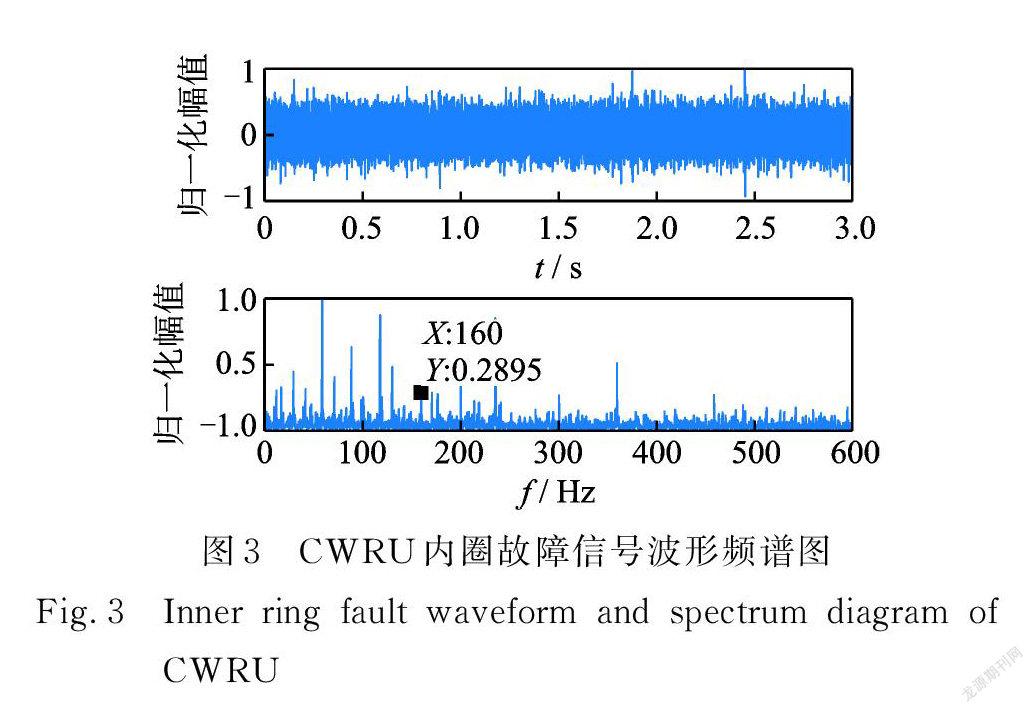
采用凱斯西儲大學公開數據集中的 SKF 深溝球軸承，故障類型為內圈及外圈故障，采樣頻率12×103 Hz，內圈故障直徑為0.014 in（0.356 mm），電機轉速為1772 r/min，計算內圈故障特征頻率約為159.9 Hz；外圈故障直徑0.021 in（0.533 mm），電機轉速1750 r/min，外圈故障頻率約為104.55 Hz。

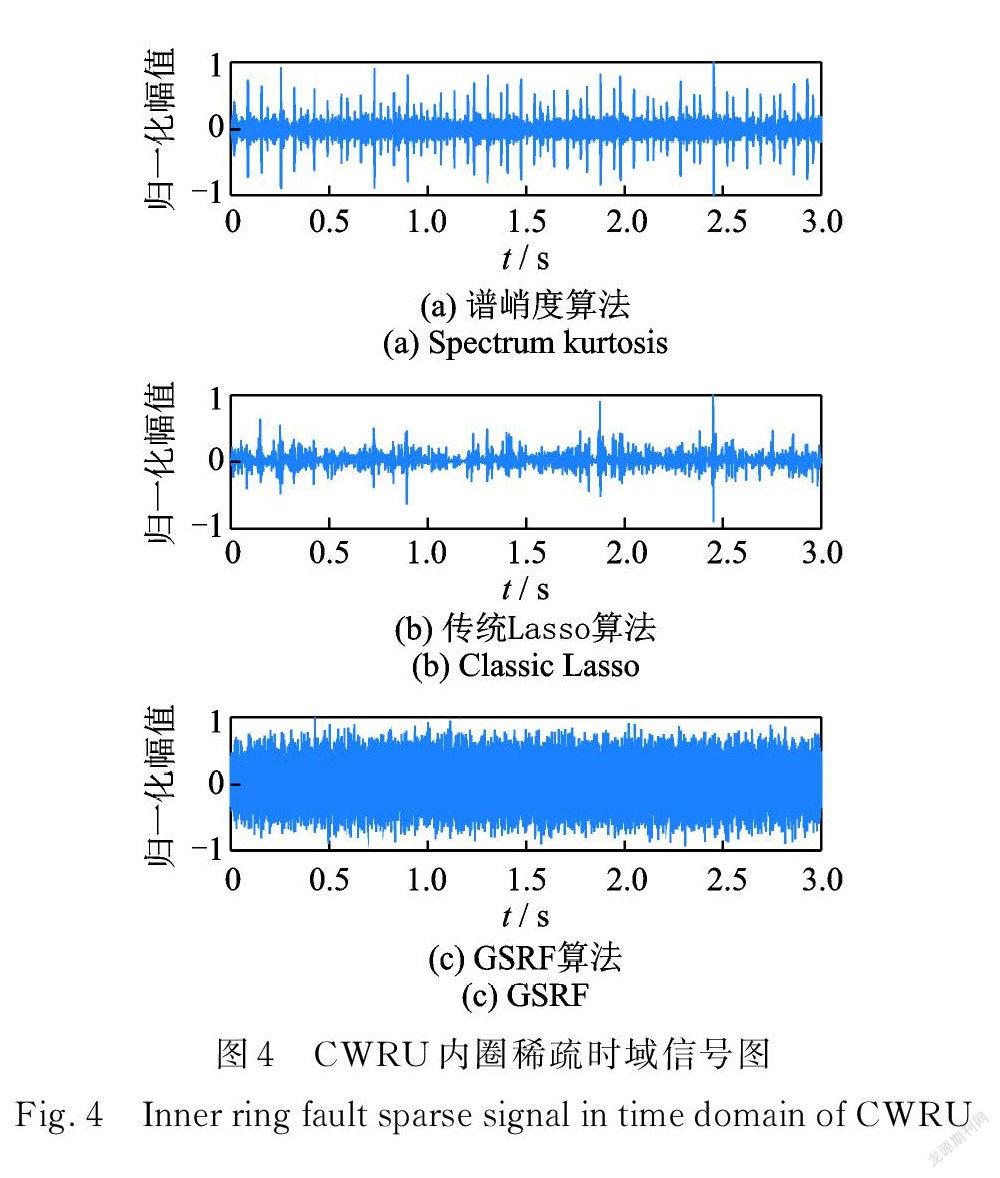
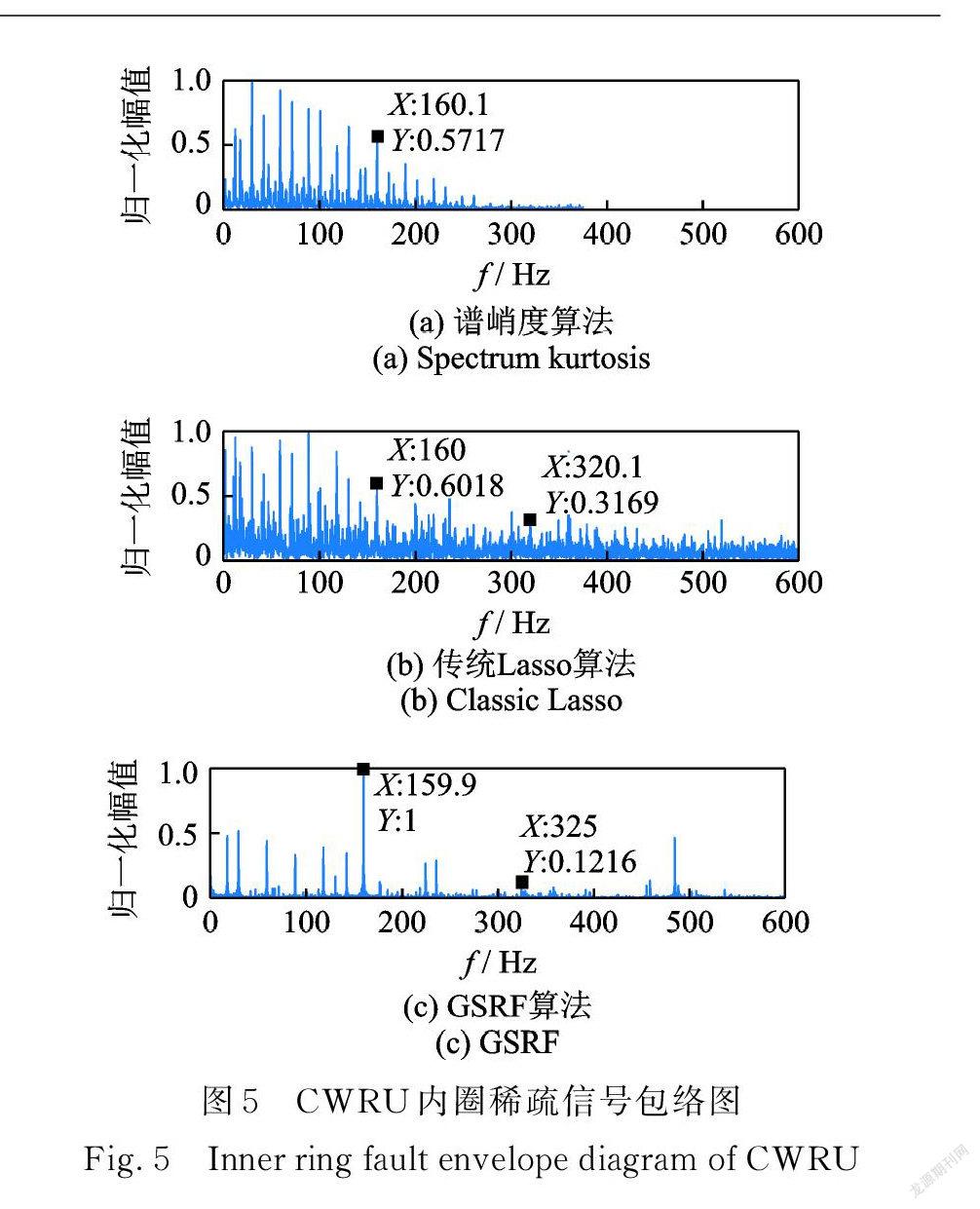
如圖3所示，內圈故障特征頻率完全被噪聲淹沒，分別以譜峭度、非重疊組結合 L21范數約束的 Lasso （傳統方法）和頻域群橋組稀疏（GSRF）做分析，圖4為時域重構信號對比圖，圖5為包絡譜對比。

所提方法綜合考慮軸承轉速、采樣頻率及頻域分辨率的影響，選取頻域信號的重疊組變量系數為20。圖4中（ a ）為譜峭度，（b）為傳統方法，（ c ）為 GSRF 。由圖3和4對比可知，譜峭度和傳統方法恢復的時域信號更稀疏，GSRF 處理后的時域信號與原始振動信號相比無明顯變化。圖 5（ a ）為譜峭度稀疏信號包絡譜，（b）為傳統方法稀疏信號包絡譜， GSRF 包絡譜如圖（ c ）所示。對比包絡譜，譜峭度和傳統方法實現了故障特征增強，但對噪聲成分的抑制效果較弱，GSRF 在增強故障特征的同時，較好地抑制了故障無關頻率成分。

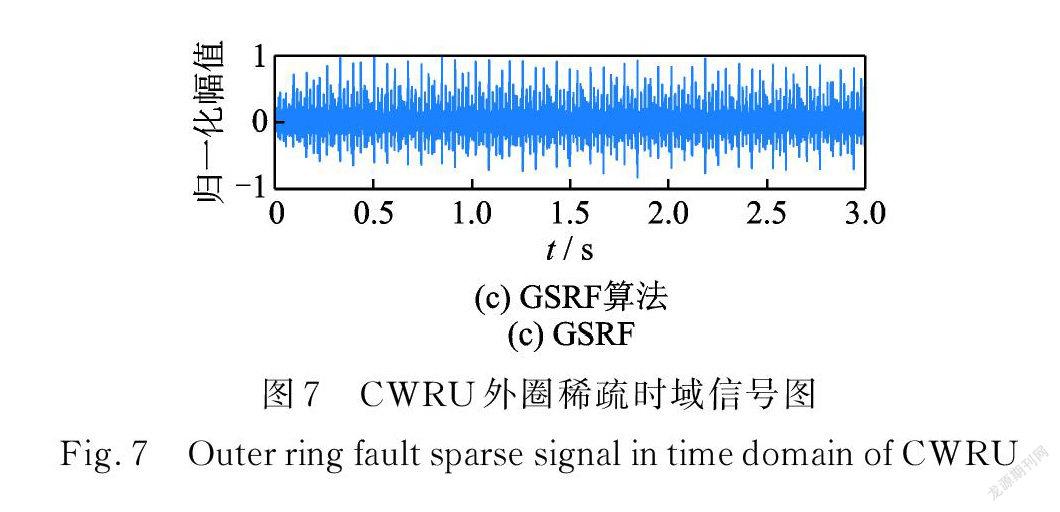
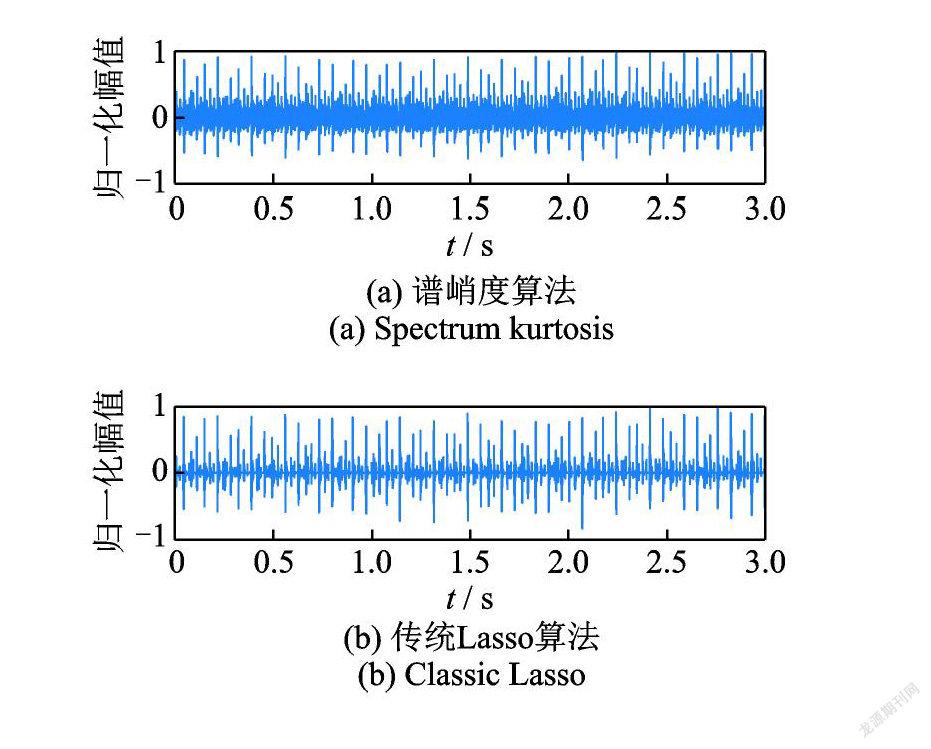
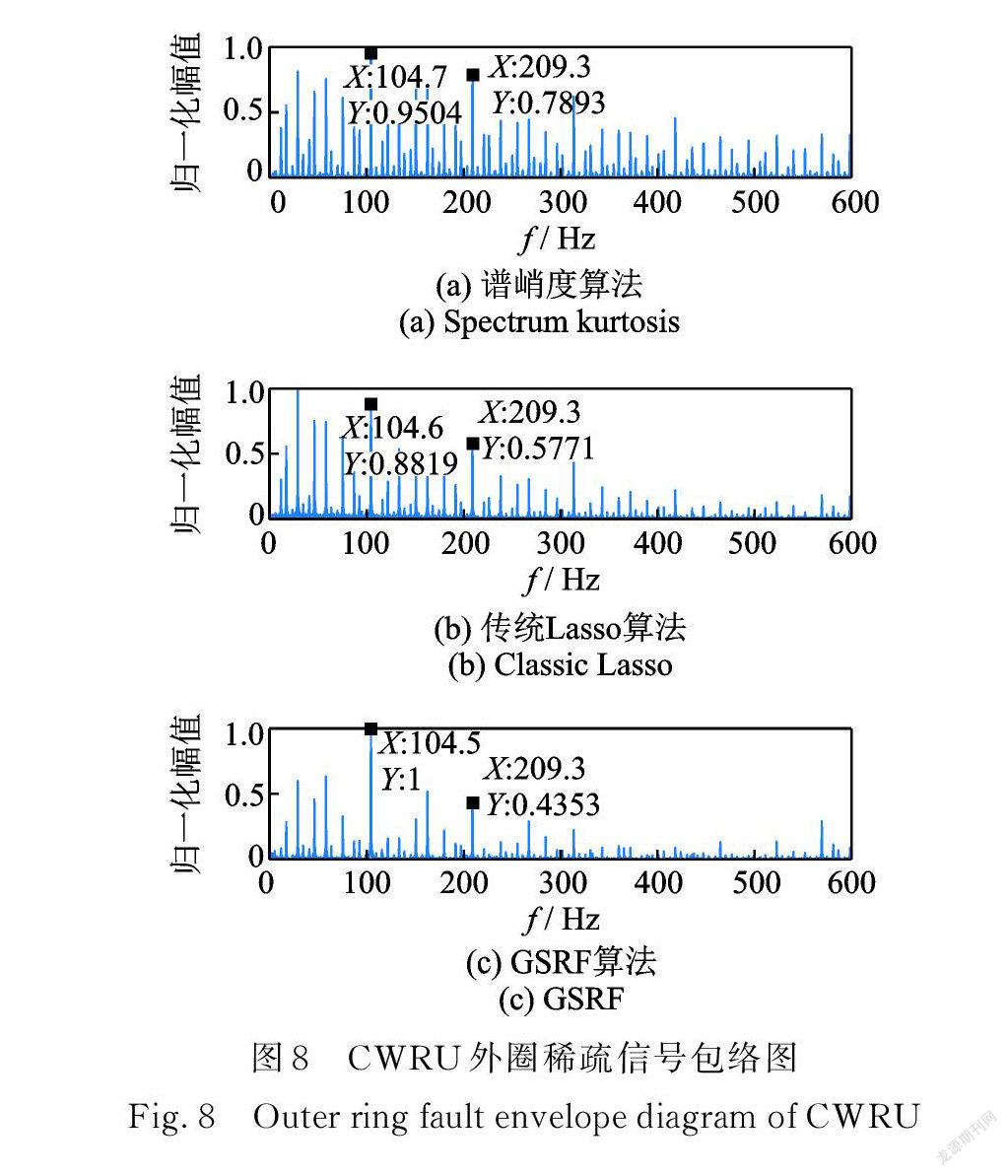
沖擊明顯，包絡譜上特征頻率受噪聲干擾。圖 7，8中（ a ），（b），（ c ）分別是譜峭度、傳統方法及 GSRF 的分析結果。對比可知，傳統方法處理后的信號在時域上更稀疏，GSRF 則在頻域上消除了更多噪聲干擾。綜合分析認為 GSRF 在稀疏分解中盡可能多的保留了沖擊信息，有效消除了故障無關成分的

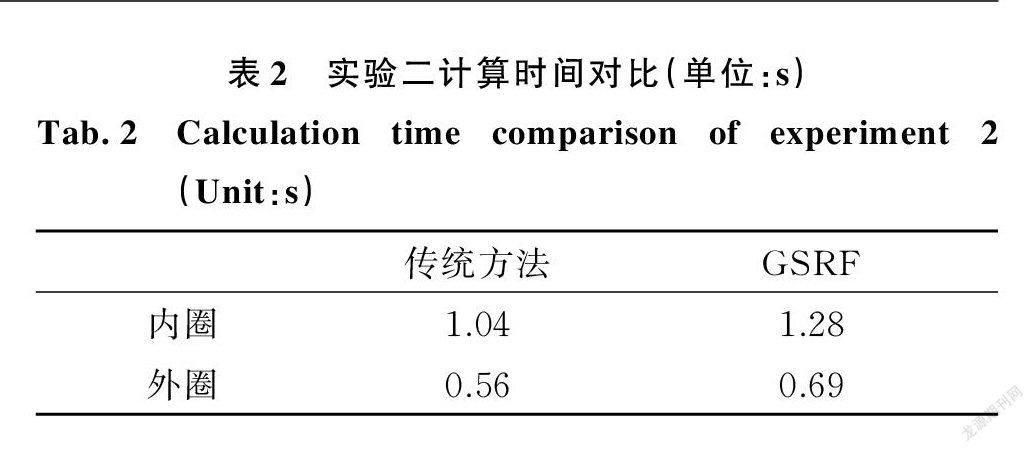
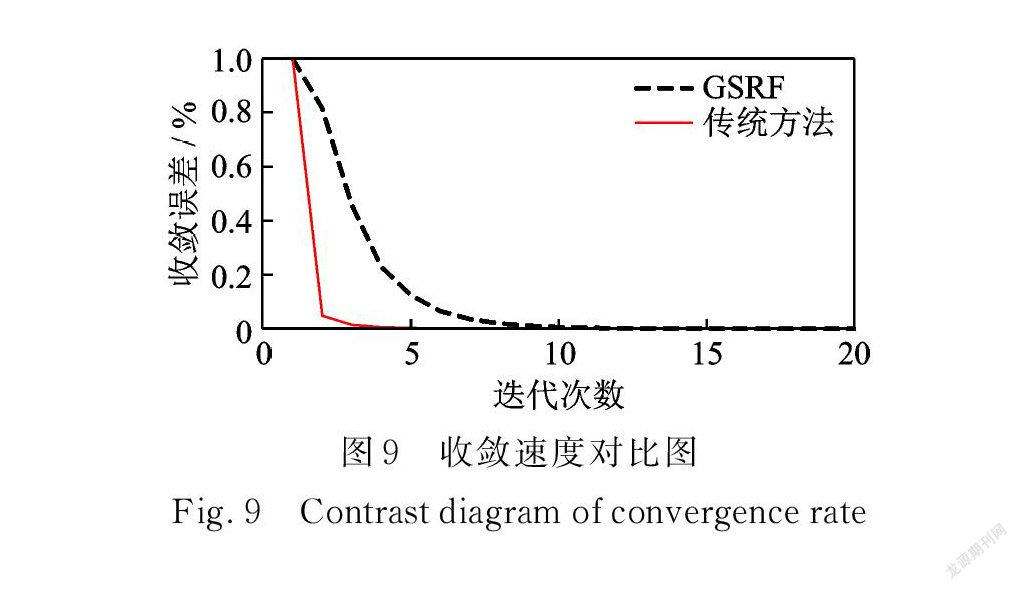
圖9中，計算復雜的 GSRF 收斂相對更慢，也能在10步內收斂。表 1記錄計算時間，分析認為 GSRF 對變量的細致篩選會降低運算速度，但卻能顯著提升診斷結果的準確性。

3.2? 實驗驗證二

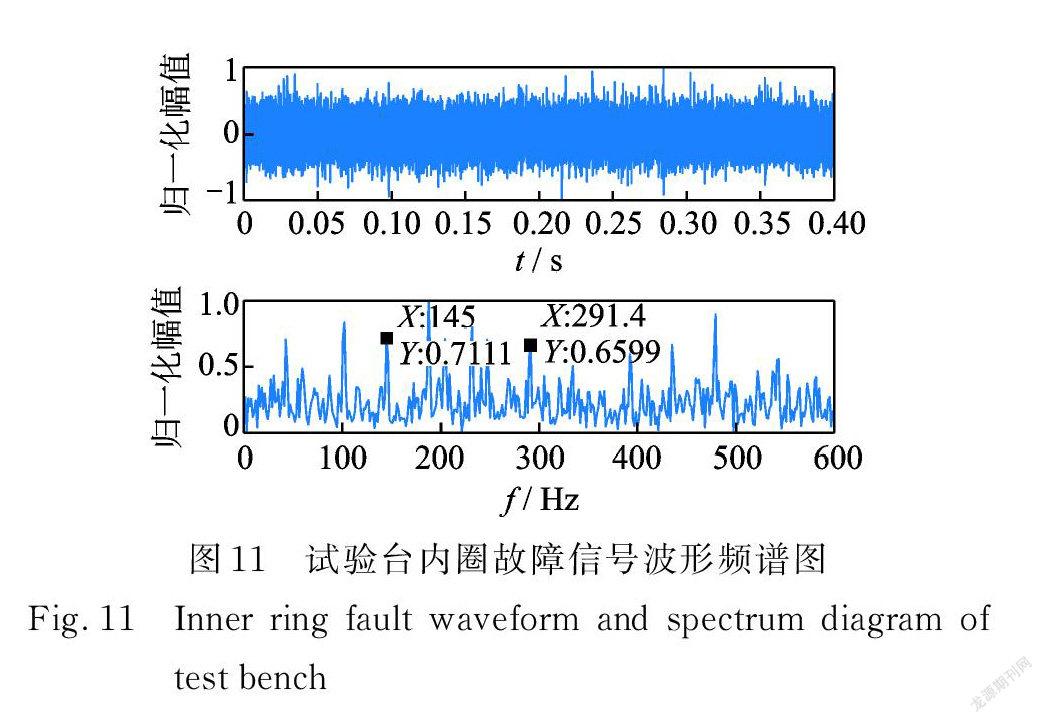
在如圖10所示的試驗臺上采集振動信號，對 N205EM 圓柱滾子軸承做水平和豎直方向的數據采樣，采樣頻率為105 Hz，電機轉速為1300 r/min，線切割加工內、外圈故障寬度均為0.3 mm，深度為0.05 mm，計算內、外圈故障特征頻率分別為145.84，86.32 Hz。

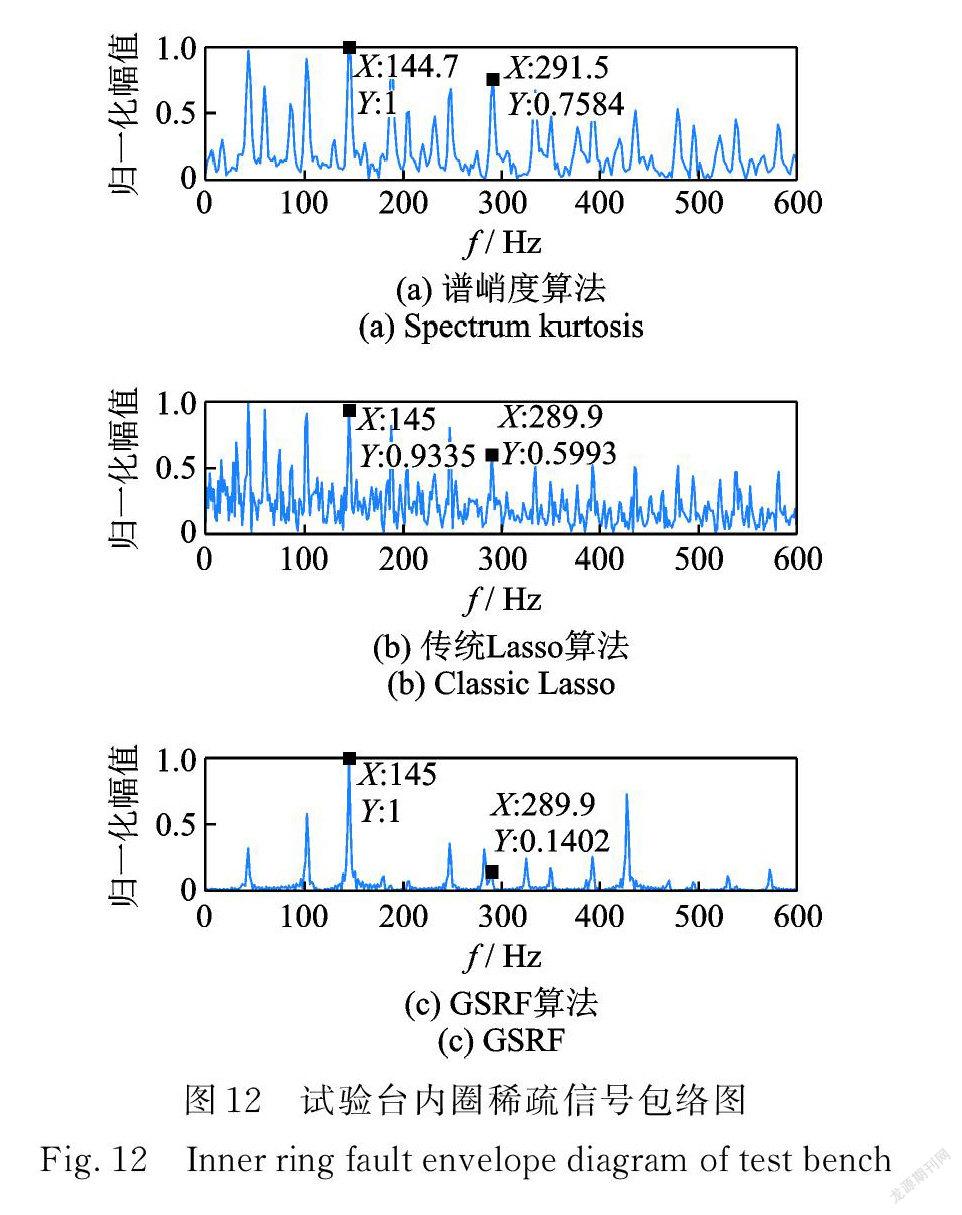
內圈故障信號時域頻譜如圖11所示，故障特征頻率已被噪聲淹沒。綜合考慮軸承轉速、采樣頻率及頻域分辨率的影響，對頻域信號按每組20個變量劃分重疊組，處理結果如圖12所示。譜峭度和傳統方法的包絡譜分析在圖12（ a ），（b）中故障特征頻率較原信號有一定增強，但仍無法消除其他噪聲成分的干擾，GSRF 處理的結果在圖12（ c ）中則有效抑制了非平穩噪聲。

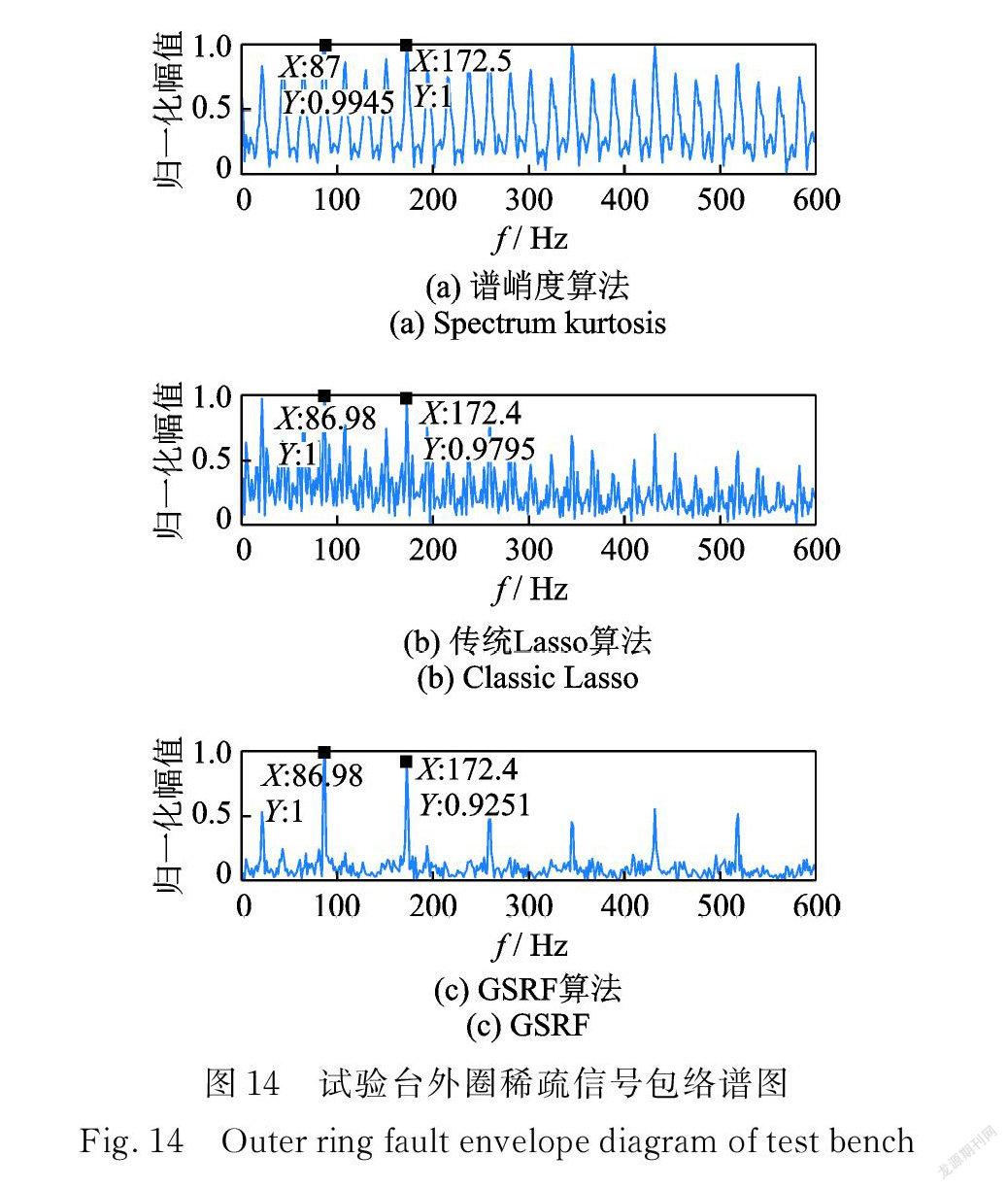
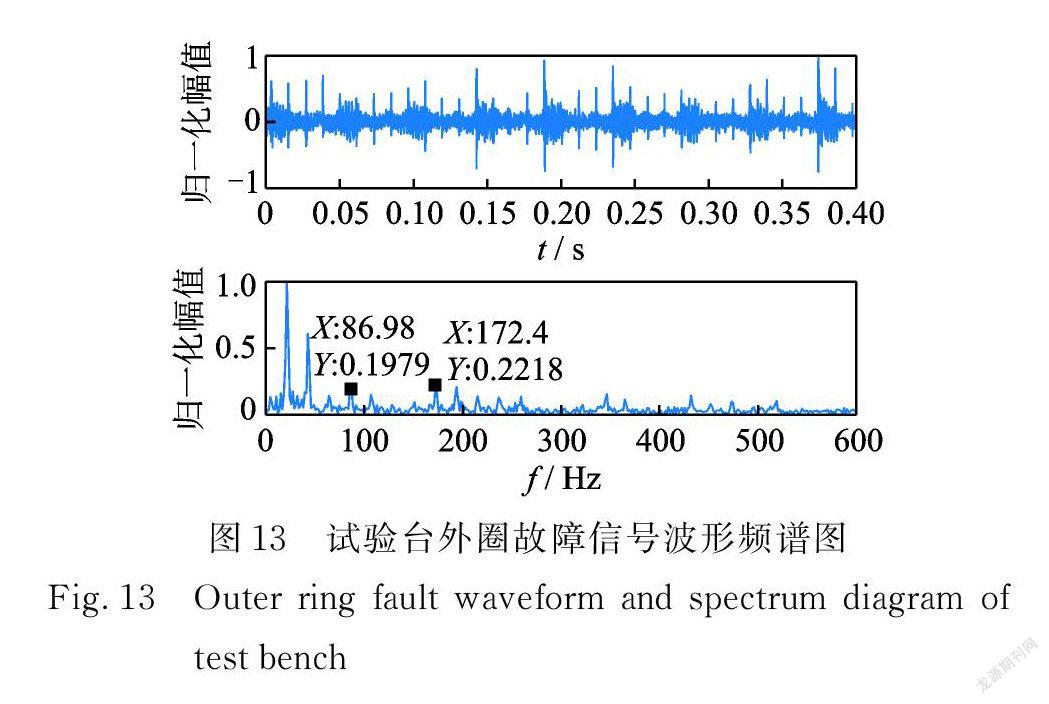
圖13為外圈故障信號的波形頻譜圖，故障特征頻率86.32 Hz 明顯被淹沒。圖 14（ a ），（b）是分別應用譜峭度和傳統方法處理后的結果，沖擊特征頻率及其高次諧波明顯被增強，但無法消除旁瓣噪聲的影響，在圖14（ c ）中故障特征頻率及其高次諧波明顯且消除了干擾。表2為傳統方法與 GSRF 計算時間對比結果，GSRF 在沒有顯著增加運算時間的情況下獲得了更好的故障識別效果，實現了微弱故障的診斷。

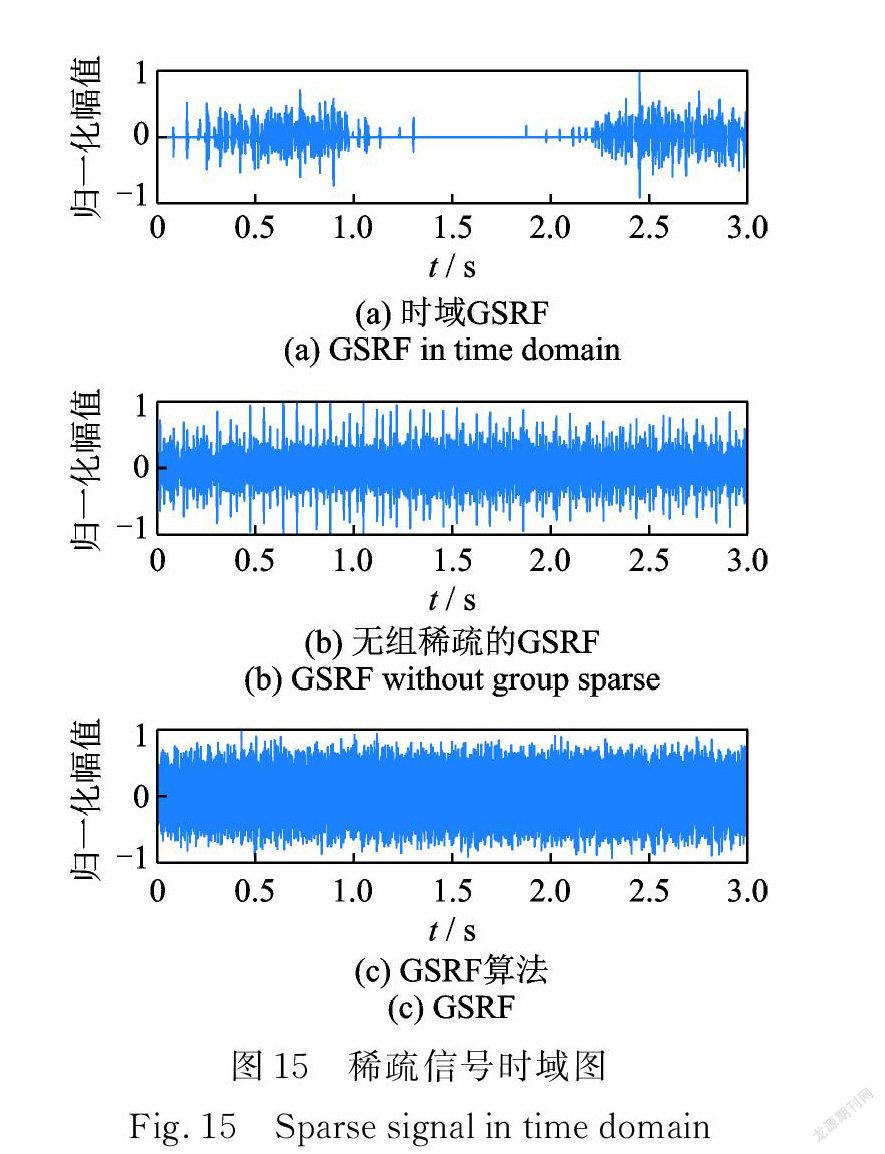
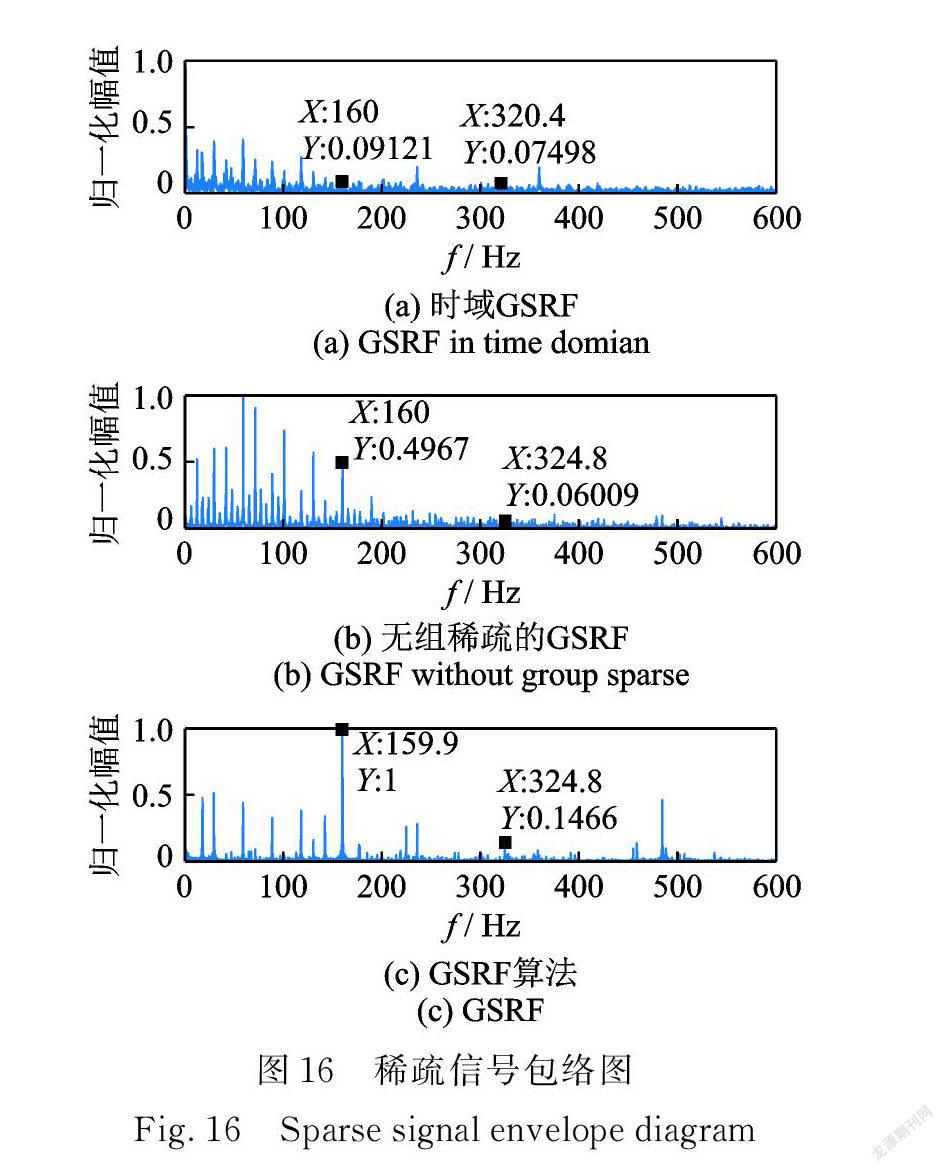
圖15和16討論了域變換和重疊組因素對分解結果的影響。圖 15和16中：（ a ）是時域重疊組橋稀疏算法分解結果；（b）是頻域無重疊組的橋稀疏算法結果，（ c ）是 GSRF 算法處理結果。

圖15（ a ），16（ a ）顯示，時域運算分解結果稀疏性較強，但故障信息丟失較多，對比圖3，15（b）和16（b），無重疊組的橋稀疏算法增強了沖擊特征，但無法實現信號與噪聲的解耦，不能提取故障特征頻率，而 GSRF 在增強故障特征的同時，抑制了故障無關頻率成分，有效提取了故障特征頻率。

4 結論

確定以最小二乘結合 L1范數約束的基礎數學回歸模型，根據故障信號沖擊特點引入組稀疏及群橋約束，提出了基于頻域組稀疏結合群橋約束的故障特征提取方法。實驗分析結果表明：GSRF 將低信噪比信號轉換至頻域進行稀疏表示，可以減弱時域非平穩噪聲擾動帶來的模式混疊影響，提高了特征提取精度。組稀疏和群橋正則化按頻率差別篩選組內、組間變量，在完整保留故障沖擊信息的同時濾除了無關頻率成分，進一步增強了故障特征。通過引入迭代重加權系數優化非凸目標函數，顯著降低運算復雜度，便于使用 ISTA 求解。與傳統非重疊組結合 L21范數約束的 Lasso 方法對比，驗證了所提方法具有較強的特征提取能力和噪聲魯棒性。

參考文獻：

[1] 陳是扦，彭志科，周鵬.信號分解及其在機械故障診斷中的應用研究綜述[ J ].機械工程學報，2020，56（17）：91-107.

Chen Shiqian，Peng Zhike，Zhou Peng . Review of sig? nal decomposition theory and its applications in machine fault diagnosis [ J ]. Journal of Mechanical Engineering，2020，56（17）：91-107.

[2] 魏永合，聶晨，李宏林. LMD 與優化 OMP 算法的滾動軸承故障診斷方法研究[ J ].沈陽理工大學學報，2020，39（3）：61-66.

Wei Yonghe，Nie Chen，Li Honglin . Study on fault di? agnosis method of rolling bearing based on LMD and op? timized? OMP? algorithm [ J ]. Journal? of? Shenyang? Li? gong University，2020，39（3）：61-66.

[3] 李華，劉韜，伍星，等. EEMD 和優化的頻帶熵應用于軸承故障特征提取[ J ].振動工程學報，2020，33（2）：414-423.

Li? Hua ，Liu? Tao ，Wu? Xing ，et? al . EEMD? andopti? mized frequency band entropy for fault feature extraction on? bearings [ J ]. Journal? of? Vibration? Engineering，2020，33（2）：414-423.

[4] 李清泉，王歡.基于稀疏表示理論的優化算法綜述[ J ].測繪地理信息，2019，44（4）：1-9.

Li Qingquan，Wang Huan . Sparse representation-based optimization：a? survey [ J ]. Journal? of? Geomatics，2019，44（4）：1-9.

[5]? Hou F，Selesnick I，Chen J，et al . Fault diagnosis forrolling bearings under unknown time-varying speed con? ditions with sparse representation[ J ]. Journal of Sound and Vibration，2021，494：115854.

[6]? Zheng? K ，Bai? Y ，Xiong? J ，et? al . Simultaneously? lowrank and group sparse decomposition for rolling bearing fault diagnosis[ J ]. Sensors，2020，20（19）：1-27.

[7]? Liang K，Zhao M，Lin J，et al . An? information-basedK-singular-value? decomposition? method? for? rolling? ele? ment? bearing? diagnosis [ J ]. ISA? Transactions ，2020，96：444-456.

[8]? Zhang X，Liu Z，Wang L，et al . Bearing fault diagnosisbased? on? sparse? representations? using? an? improved OMP? with? adaptive? Gabor? sub-dictionaries [ J ]. ISA Transactions，2020，106：355-366.

[9]? Wang B，Liao Y，Ding C，et al . Periodical sparse low-rank? matrix? estimation? algorithm? for? fault? detection? of rolling? bearings [ J ]. ISA? Transactions ， 2020， 101：366-378.

[10] Zheng? Kai ，Yang? Dewei，Zhang? Bin ，et? al . A? groupsparse representation method in? frequency domain with adaptive? parameters? optimization? of&nbsp; detecting? incipient rolling? bearing? fault [ J ]. Journal? of? Sound? and? Vibra ? tion，2019，462：114931.

[11] Zhang W，Yu D，Yan X，et al . Weak multiple fault de?tection? based? on? weighted? morlet? wavelet-overlapping group sparse for rolling bearing fault diagnosis[ J ]. Ap? plied Sciences，2020，10（6）：2057.

[12] DiwuZhenkun，Cao Hongrui，Wang Lei，et al . Collab ?orative? double? sparse? period-group? Lasso? for? bearing fault diagnosis[ J ]. IEEE? Transactions on Instrumenta ? tion and Measurement，2021，70：1-10.

[13] An B，Zhao Z，Wang S，et al . Sparsity-assisted bearingfault diagnosis using multiscale period group Lasso[ J ]. ISA Transactions，2019，98：338-348.

[14] Zhao? Z ，Wang? S ，Sun? C ，et? al . Sparse? multiperiodgroup? Lasso? for bearing multifault diagnosis[ J ]. IEEE Transactions? on? Instrumentation? and? Measurement，2019，69（2）：419-431.

[15] Zhao Z，Wu S，Qiao B，et al . Enhanced sparse period-group Lasso for bearing fault diagnosis[ J ]. IEEE Trans ?actions on Industrial Electronics ，2019，66（3）：2143-2153.

[16]王華慶，任幫月，宋瀏陽，等.基于終止準則改進 K-SVD 字典學習的稀疏表示特征增強方法[ J ].機械工程學報，2019，55（7）：35-43.

Wang? Huaqing，Ren? Bangyue，Song? Liuyang，et? al .Sparse representation method based on termination crite? ria improved K-SVD dictionary learning? for feature en? hancement [ J ]. Journal? of? Mechanical? Engineering，2019，55（7）：35-43.

[17] Yuan M，Lin Y . Model selection? and? estimation in re ?gression with grouped variables[ J ]. Journal of the Royal Statistical Society：Series B，2006，68（1）：49-67.

[18] Huang J，Ma S，Xie H，et al . A group bridge approachfor? variable? selection [ J ]. Biometrika，2009，96（2）：339-355.

[19] Wang? X ，Wang? M . Adaptive? group? bridge? estimationfor high-dimensional partially linear models[ J ]. Journal of Inequalities and Applications，2017，2017（1）：1-18.

[20] Li? G ，Liu? X ，Chen? K . Integrative? multi-view? regres?sion：bridging? group-sparse? and? low-rank? models [ J ]. Biometrics，2019，75（2）：593-602.

[21] Park? C ，Yoon? Y? J . Bridge? regression ：adaptivity? andgroup selection[ J ]. Journal of Statistical Planning & In? ference，2011，141（11）：3506-3519.

[22] Burrus C? S，Barreto J A，Selesnick I W . Iterative re ?weighted? least-squares? design? of FIR? filters [ J ]. IEEE Transaction on Signal Processing，1994，42（11）：2926-2936.

[23]劉建偉，崔立鵬，羅雄麟.組稀疏模型及其算法綜述[ J ].電子學報，2015，43（4）：776-782.

Liu? Jianwei， Cui? Lipeng， Luo? Xionglin . Survey? on group sparse models and algorithms[ J ]. Acta Electroni? ca Sinica，2015，43（4）：776-782.

Fault feature extraction using group sparse representation in frequency domain

WANG Hua-qing1，LIU Ze-yuan1，LU Wei2，SONG Liu-yang1，HAN Chang-kun1????????????????? （1.College of Mechanical and Electrical Engineering，Beijing University of Chemical Technology，Beijing 100029，China；

2.Institute of Engineering Technology，Sinopec Catalyst Company Limited，Beijing 101100，China）

Abstract： A fault feature extraction method based on group sparsity and improved iterative shrinkage threshold optimization in fre ? quency domain （GSRF） is proposed to solve the issues in rolling bearing diagnosis about difficulty in mathematical model determi? nation，sparse constraints and optimization algorithm selection . The vibration signals are converted into the frequency domain and the variables? are divided by? overlapping rules . The? least square regression model with? group bridge? constraint is? constructed to screen impact related variables accurately . The iterative reweighting coefficient is introduced to simplify the equation，so that the sparse signal in frequency domain can be solved by iterative shrinkage-thresholding algorithm . The envelope spectrum analysis of reconstructed sparse signal in time domain is carried out to extract the fault features . The experimental results show that the pro? posed algorithm is superior to the traditional group sparse LASSO combined with L21 norm constraint . GSRF can effectively ex? tract weak fault features and achieve bearing fault diagnosis in the sparse domain .

Key words ： fault diagnosis；rolling bearing；weak fault；sparse representation；feature extraction

作者簡介：王華慶（1973—），男，教授。電話：13801023830；E-mail：hqwang@mail .buct .edu .cn。

通訊作者：宋瀏陽（1988—），女，副教授。E-mail：xq _0703@163.com。