聚焦思維支點 凸顯意義本質
胡鳳仙






[摘 要]要在單元復習課上讓學生打開思路,就要對單元核心概念進行分析,從而幫助學生突破數學學習中的難點,促使學生深度理解,讓單元復習課真實有效。以“分數的意義和性質”單元復習課為例,聚焦多個思維支點,巧用思維導圖,引用學生作品,借用學習材料,運用生活情境,活用個性檔案,優化練習內容。
[關鍵詞]分數的意義和性質;單元復習課;練習設計
[中圖分類號] G623.5 [文獻標識碼] A [文章編號] 1007-9068(2022)23-0069-03
單元復習課是小學數學中的一種重要課型。筆者在“分數的意義和性質”單元復習課中,首先對單元核心概念進行分析,再聚焦多個思維支點,設計針對性練習來幫助學生突破學習中的難點,讓單元復習課真實有效。
“分數的意義”是“分數的意義和性質”單元的核心概念。三年級學生已經對分數有初步認識。“分數的意義”是用分數表征數量和數量之間的關系,但只注重表征部分和整體的關系,忽視了用分數表征量的屬性,使得學生在后續學習時有不少困擾,學生不理解分數的意義,當同時出現用分數表征“量”和“率”時,學生就不能準確區分,嚴重影響了后續學習。
橫向重構單元復習課的練習,可以把練習重構為生活型、問題型、概念型、反思型、綜合型、生活型。基于此,可在縱向上將練習設計成課前的前置練習、課中有驅動性的練習及課后作業。聚焦思維支點,縱橫交織,多維度定位單元復習課的練習內容。
一、巧用思維導圖,形成系統找困惑
在教學單元知識后,教師整合教學內容,巧用思維導圖,設計具有開放性、針對性的問題,詳略得當,突出知識重難點和思想方法。學生借用思維導圖厘清知識,并找出困惑之處。
課前,學生先完成前置性練習,對知識進行回顧、整理,在復習課上才能突破難點,解決問題。
【前置性練習——綜合型】
練習內容:整理“分數的意義和性質”單元的知識。
【反饋分析】
有些學生對分數的意義理解不到位。而通過思維導圖,學生可以自主找出困惑點,教師針對學生的困惑點找出本節課的重難點,繼續通過不同的思維支點來幫助學生深入理解分數的意義。
二、引用作品呈現,凸顯分層找差異
針對學生對分數意義不同層次上的理解,教師選擇學生的典型作品,幫助學生進一步理解分數的意義。
【驅動性練習——概念型】
練習內容:這些作品都表示3/4(如圖2),它們的意義一樣嗎?
【反饋分析】
在學生根據作品說分數的意義時,教師引導學生看前三幅作品的相同之處。學生意識到:前三幅作品都是把單位“1”平均分成4份,取其中的3份,是把一個“大”整體看作單位“1”;第四幅作品是把“小”整體看作單位“1”。
在練習中,不同的學生能通過畫圖來表征分數的“率”。教師引導學生再次表征分數的具體意義,成功喚醒了學生的已學知識。學生在比較中再次明確單位“1”的不同含義:“大”整體或“小”整體。
三、借用學習材料,發散思維探深度
借用立方體組合設計出進階式練習題組,可幫助學生深入理解用分數表征“率”這一知識點。
【驅動性練習——生活型】
練習內容:如何表示3/4??
2.在圖中,你還能找到3/4嗎? (請用文字表述)
3.在立體圖形的左邊加1列小正方體,你還能找到3/4嗎?你覺得怎樣繼續加才能又得到3/4?
(請記錄自己的想法)
【反饋分析】
1.你會怎樣表示[34]呢?
學生發現可以在這16個正方體中隨意選12個涂顏色,就可以得到3/4。
學生解釋:涂色部分是整體的12/16,通過化簡得到3/4。
學生能悟到分數與除法的關系,這其實是個思維深入的過程,即從部分與整體的關系中找出3/4。
2.在圖中,你還能找到3/4嗎?
學生得出:往上、下加一層或多層小立方體也能得到3/4。
這題讓學生領悟到“萬變不離其宗”的思想。
3.在立體圖形的左邊加1列小正方體,你還能找到3/4嗎?你覺得怎樣繼續加才能得到3/4?
學生表示只找到了“4/5”:把單位“1”平均分成5份,涂色部分占了4份。教師追問:“如果繼續在左邊加1層、2層……那分別可以得到哪些分數?”學生寫出了5/6,6/7,7/8?…… 教師追問:“這些分數有什么特點呢?”學生觀察得出:它們的分子總比分母少1,越往后,分數越大,越接近1。
“如果在它的右邊加1層、2層、3層,再往下加呢?”學生表示:得到分數3/5,3/6,3/7……分子一直是3,分母逐漸增大,不可能出現3/4的。
教師用課件出示右邊加3層的圖形(如圖4),引導學生找其中的[34]:涂色部分是白色部分的3/4。學生對比前后得到的3/4的不同之處:單位“1”不同,前面的單位“1”是指整個圖形,而現在的單位“1”是指白色部分。
分數不僅可以表示部分與整體的關系,還可以表示一部分與另一部分的關系,但表示的這兩種關系都是用分數表示“率”。
可見,第3題更具挑戰性,因為它蘊含了極限思想。借用直觀圖形設計的進階式練習題組把分數的意義引向了深處,培養了學生的數學思維。
四、運用生活情境,巧設題組解困惑
針對學生未能正確區分用分數表征“量”和“率”的現象,可依托學校科普園種地情境,通過改變土地面積的大小來設計針對性練習題組,以幫助學生解開困惑。
【驅動性練習——問題型】
練習內容:究竟哪個小隊種植番茄的面積大?(如圖5)
【反饋分析】
學生結合圖示厘清第1題的思路:陽光小隊和雛鷹小隊都認領了1平方米,就是把1平方米平均分成4份,其中3份就是3/4平方米,因此,兩小隊種植番茄的面積一樣大。
教師引導學生結合圖示(如圖6)厘清第2題的思路:陽光小隊菜地的3平方米的3/4,可以先把3平方米先平均分成3份,再把其中1份,也就是1平方米平均分成4份,這樣的3份就是3/4平方米,有3個這樣的3/4平方米。雛鷹小隊用菜地的3/4平方米,也就是1平方米的3/4。
第3題中哪個小隊種植番茄的面積更大呢?
學生有了以上經驗,能從單位“1”入手,找到陽光小隊用來種番茄的菜地面積是以[34]平方米為單位“1”,把它平均分成4份,其中的3份種植番茄。而雛鷹小隊用了[34]平方米種番茄,也就是用了全部土地來種植番茄,那當然是雛鷹小隊種植番茄的面積大。
教師點撥:“這三題的區別在哪里?”學生得出:“兩個小隊認領的菜地分別是1平方米、3平方米和3/4平方米。”師生共悟:因為單位“1”的變化得到的陽光小隊種植番茄的菜地面積不一,但雛鷹小隊的一直是3/4平方米。
“究竟哪個小隊種植番茄的面積大?”練習題組是整節課中的“重頭戲”,也是難點。當用分數表征“量”和“率”同時出現時,大部分學生不能正確區分,而結合學校科普園種地的情境,用圖示法來突破這一難點,恰到好處。
五、活用個性檔案,整理思路致通透
收集典型易錯題也是單元整理與復習的一部分,強調對典型易錯題的分析與應用。引導學生從四個方面整理典型易錯題,把解題思路弄清楚,進而建立每個單元的個性檔案資源。
【學后性練習——反思型】
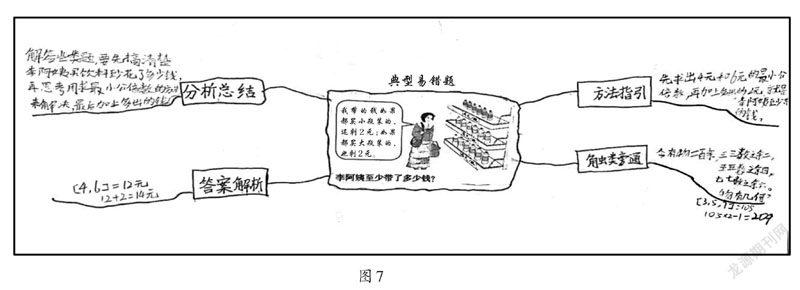
練習內容:用思維導圖來整理本單元的典型易錯題(如圖7)。
【反饋分析】
學生從答案解析、分析總結、方法指引、觸類旁通四個方面來分析典型易錯題,學生用思維導圖收集典型易錯題,可自行完成,也可同伴互助。通過平時不斷地積累,學生建立個性檔案,教師也能夠利用這些個性化檔案進行備課。
在單元復習課中,教師可在核心概念的基礎上,聚焦思維支點,設計出有針對性的練習。學生在“小貼士”引導下完成有指向性、有主題,以及承載著解惑任務的練習,突破數學學習中的重難點,做到深度理解,讓單元復習課真實有效。

