雙向全橋LLC諧振變換器的數字控制設計與仿真

高 林，陳 瑛

（南昌大學信息工程學院，江西 南昌 330000）

0 引 言

隨著電力電子技術的發展，電力電子器件組成的變換器正向著高效率、高頻率、高功率密度方面發展，但是功率開關器件的損耗嚴重阻礙了這一發展趨勢。功率開關器件開關頻率越高損耗就越大，轉換效率就會越低，而且給變換器的散熱帶來了巨大挑戰。要提高變換器的開關頻率就必須要減小功率開關器件的開關損耗，因此，零電壓零電流軟開關技術應運而生，LLC諧振變換器具有能夠在全負載范圍實現變壓器原邊功率開關管的零電壓開通（Zero Voltage Switch，ZVS）與變壓器副邊功率開關管近似零電流關斷（Zero Current Switch，ZCS），極大地降低開關管高頻化帶來的開關損耗。本文利用基波近似法（Fundamental Harmonic Approximation，FHA）分析了LLC變換器拓撲諧振網絡的基波等效電路模型，并得出全橋LLC諧振變換器的電壓增益特性，提出了雙向全橋LLC諧振變換器的電壓環電流環雙環控制技術，通過對LLC諧振網絡的電流進行整流濾波采樣，得到內環電流環的反饋信號，以便于DSP數字控制，數字控制技術將會是電源控制技術的發展趨勢。通過PSIM軟件進行仿真，仿真結果驗證了其可行性和正確性。

1 全橋LLC諧振變換器結構與工作原理

1.1 全橋LLC諧振變換器結構分析

全橋LLC諧振變換器的結構拓撲如圖1所示，V1為原邊側直流電源，V2為副邊側直流電源，S1～S4組成全橋原邊側的開關管，S5～S8組成全橋副邊側的開關管，Cr、Lr和Lm為組成LLC諧振的諧振電容與諧振電感。

圖1 雙向LLC諧振變換器

LLC諧振變換器有2個諧振頻率，其中一個是Lr與Cr形成的諧振頻率fr，由于勵磁電感Lm被變壓器副邊輸出電壓箝位，因此勵磁電感Lm不參與諧振。當勵磁電流Im諧振與電流Ir相等時，此時勵磁電感Lm參與諧振，而諧振頻率為fm、fr與fm的表達式為

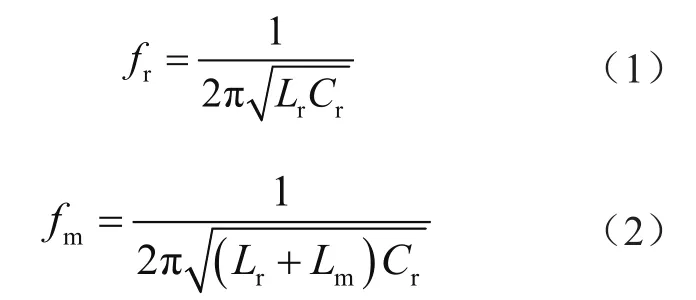
1.2 全橋LLC諧振變換器工作模式分析

全橋LLC諧振變換器根據開關頻率fs的范圍具有3種工種模式，即fs＞fr、fs=fr和fm＜fs＜fr。由于最后一種工作模式包含了各種模態，因此在此只分析最后一種工作模式，其主要工作波形如圖2所示。

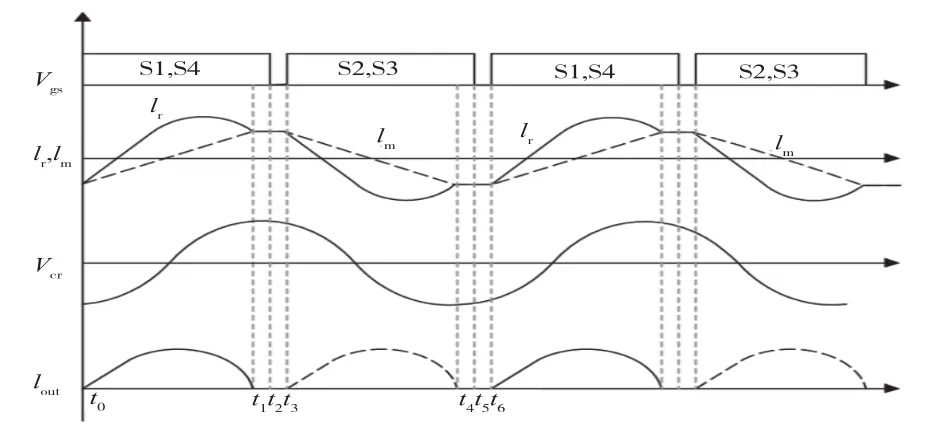
圖 2 fm＜fs＜fr時工作波形

開關階段1[t0～t1], 在t0時刻，開關管S2與S3關斷，諧振電感電流Ir給功率開關管S2與S3漏源極之間的寄生電容Coss 充電，同時給開關管S1與S4漏源極之間的寄生電容Coss進行放電。開關管S1與S4的漏源電壓Vds開始下降，當降到0時其體二極管開始導通，為S1與S4的零電壓開通提供了條件。勵磁電感Lm上的端電壓被鉗位在nVo，是由于變壓器副邊功率開關管的體二極管導通引起，其中n為變換器匝比，此時只有Cr和Lr參與諧振，Lm不參與諧振過程，諧振頻率為fr。

開關階段2[t1～t2], 在t1時刻，諧振電流與勵磁電流相等，此時流入變壓器原邊電流減小到零，副邊開關管的體二極管也相應的減小到零，實現了副邊體二極管的零電流軟關斷。勵磁電感Lm開始與Cr和Lr諧振，由于副邊電壓對勵磁電感Lm的箝位作用消失，此時諧振頻率為fm。由于Lm很大而且諧振頻率小，此時可近似Ir=Im。

開關階段3[t2～t3], 在t2時刻，開關管S1和S4關斷，S2和S3的體二極管續流導通。變壓器繞組原邊電壓極性為上負極下正極，變壓器副邊開關管的體二極管開始導通。由于此前變壓器副邊開關管的體二極管的電流已經為0，故在換流期間變壓器繞組副邊沒有存在反并聯體二極管的反向恢復過程問題。此時變壓器的副邊開關管的體二極管恢復導通，勵磁電感Lm上的電壓再被箝位到-nVo，Lm不參與諧振過程，此時勵磁電流Im是線性下降的，諧振頻率為fm。

下半個周期和上面的工作過程相似，只是方向相反，這里不再詳細說明。從上面的分析可看出原邊功率開關管S1和S4實現零電壓軟開通，變壓器副邊功率開關管反并聯體二極管實現零電流軟關斷，減小損耗，提高了效率[1]。

2 基于FHA的諧振網絡等效電路模型建立與分析

FHA僅考慮分析LLC諧振變換器在基波下的分量,去掉幅值較小的高次諧波分量,使用經典的線性交流分析法建立了穩態下的FHA等效電路模型，因此本文利用FHA的建模方式，可準確地對諧振變換器進行小信號建模及分析，全橋LLC諧振變換器的諧振網絡部分可以等效為如圖3所示的等效電路。

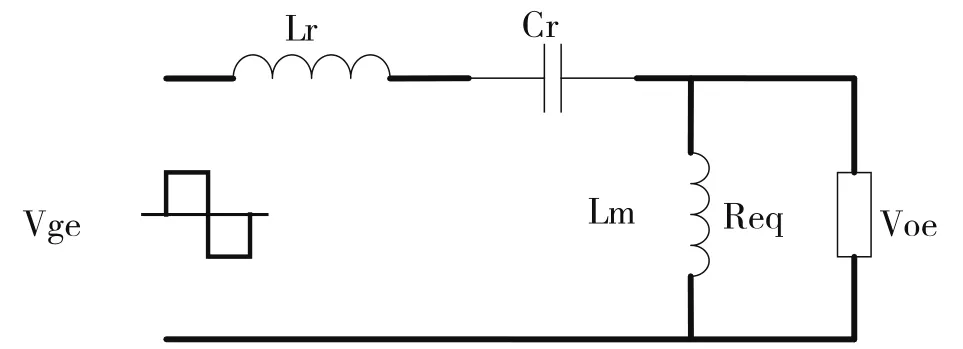
圖3 LLC變換器的諧振網絡等效電路

負載電阻折算到原邊等效電阻Req為

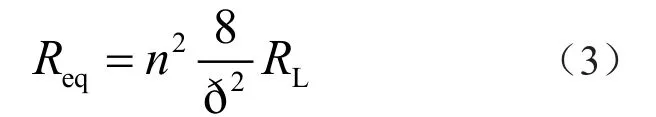
由圖3諧振網絡等效電路得到交流基波的電壓增益為

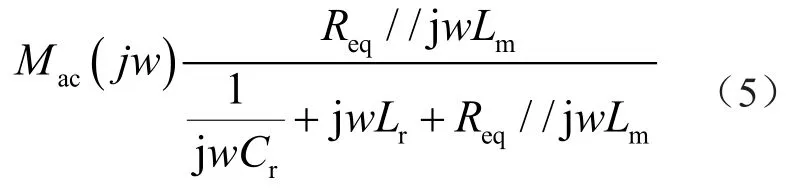
3 全橋LLC諧振變換器特性分析

根據全橋LLC的直流增益傳遞函數Mdc(fn,k,Q)，可以畫出其在不同的取值下的直流增益曲線圖。對固定k或固定Q兩種情況下的特性分析如下。

（1）當k固定時，增益在不同Q值下的頻率特性如圖4所示。

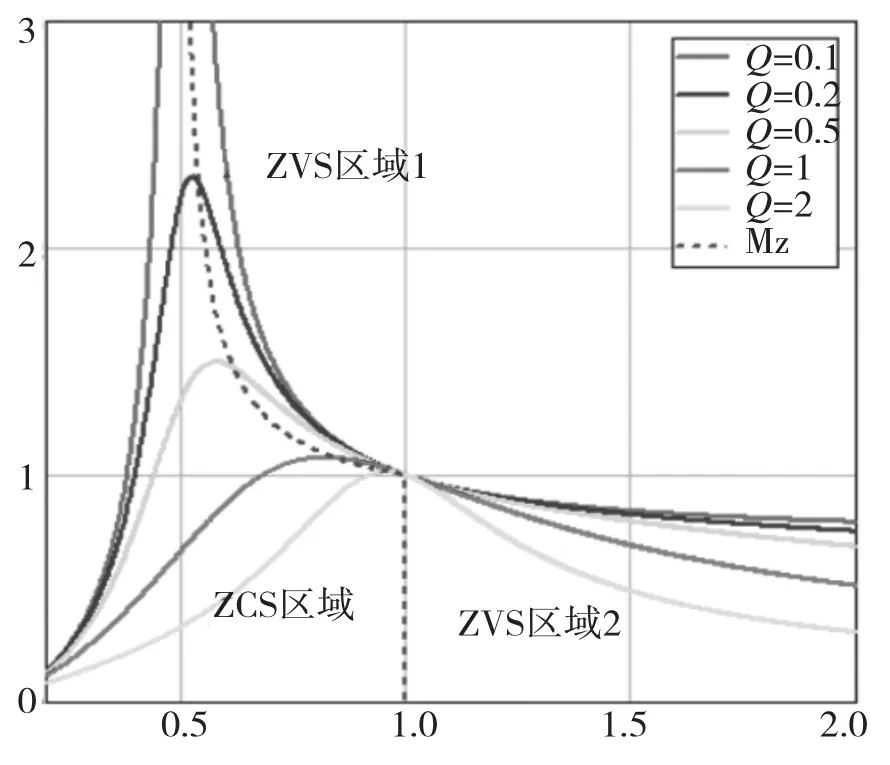
圖 4 全橋 LLC 的頻率特性

由圖4可以看出，電壓增益的頻率特性圖可以分為3個工作區域，即ZVS區域1、ZVS區域2和ZCS區域。ZVS區域1與ZVS區域2為開關管零電壓開通區域，ZVS區域為零電流關斷區域。隨著Q值增大，電壓直流增益的最大值也相應減小，Q取不同值對應著不同的最大直流增益。當fn=1時對應的電壓增益不隨負載的變化而改變，不會再受到負載的影響，因此，通常將額定頻率工作點設計在諧振頻率附近。Q值的選取原則在滿足滿載下且最低輸入電壓的直流電壓增益時，選取盡可能大的Q值。

（2）當Q固定時，不同k取值對頻率特性的影響如圖5所示。

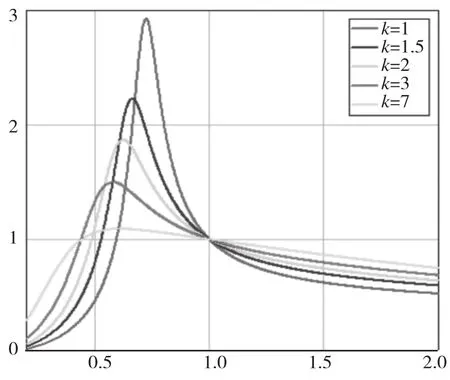
圖5 參數k對頻率特性的影響

由圖5可以看出，當Q值一定時，隨著k的增大，最大增益逐漸減小。如果k取值較大，當輸入電壓較低時，可能無法達到需要保持的輸出電壓,除了將增大諧振變換器的工作頻率變化范圍外，還降低直流電壓增益造成不滿足輸出設計要求。但是k取值較小時，勵磁電感Lm也較小，導致流過勵磁電感電流過大而使損耗增加，使變換器的效率降低。因此在選擇k值時常常折中選擇，一般取3～7比較合適[2,3]。

4 全橋LLC諧振變換器參數選取和小信號建模

為驗證前面提出雙向全橋LLC諧振變換器的電壓環和電流環雙環控制技術方案的可行性和電壓增益模型的正確性，表1列出了全橋LLC諧振變換器仿真模型的主要規格參數。

表1 全橋LLC諧振變換器仿真模型的主要規格參數

使用擴展描述函數法（Extended Describing Function，EDF）來獲得 全橋LLC諧振的小信號模型，EDF法是在諧波平衡理論的基礎上被提出的[4,5]。

使用EDF分別得到設計參數如表1所示的輸出電壓對開關頻率的傳遞函數，諧振電感電流對開關頻率的傳遞函數Gvw(S),Giw(S)波特圖如圖6所示。

圖6 Gvw(S),Giw(S)波特圖

5 雙向全橋LLC變換器仿真分析

本文以5 kW的變換器為例，電路參數取值如表1所示，使用PSIM仿真軟件對雙向全橋LLC諧振變換器進行仿真(正向功率傳輸)，仿真電路如圖7所示，瞬間加滿載的仿真波形如圖8所示。

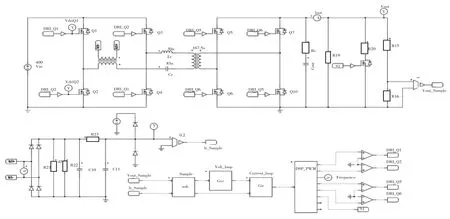
圖7 全橋LLC諧振變換器全橋的仿真電路

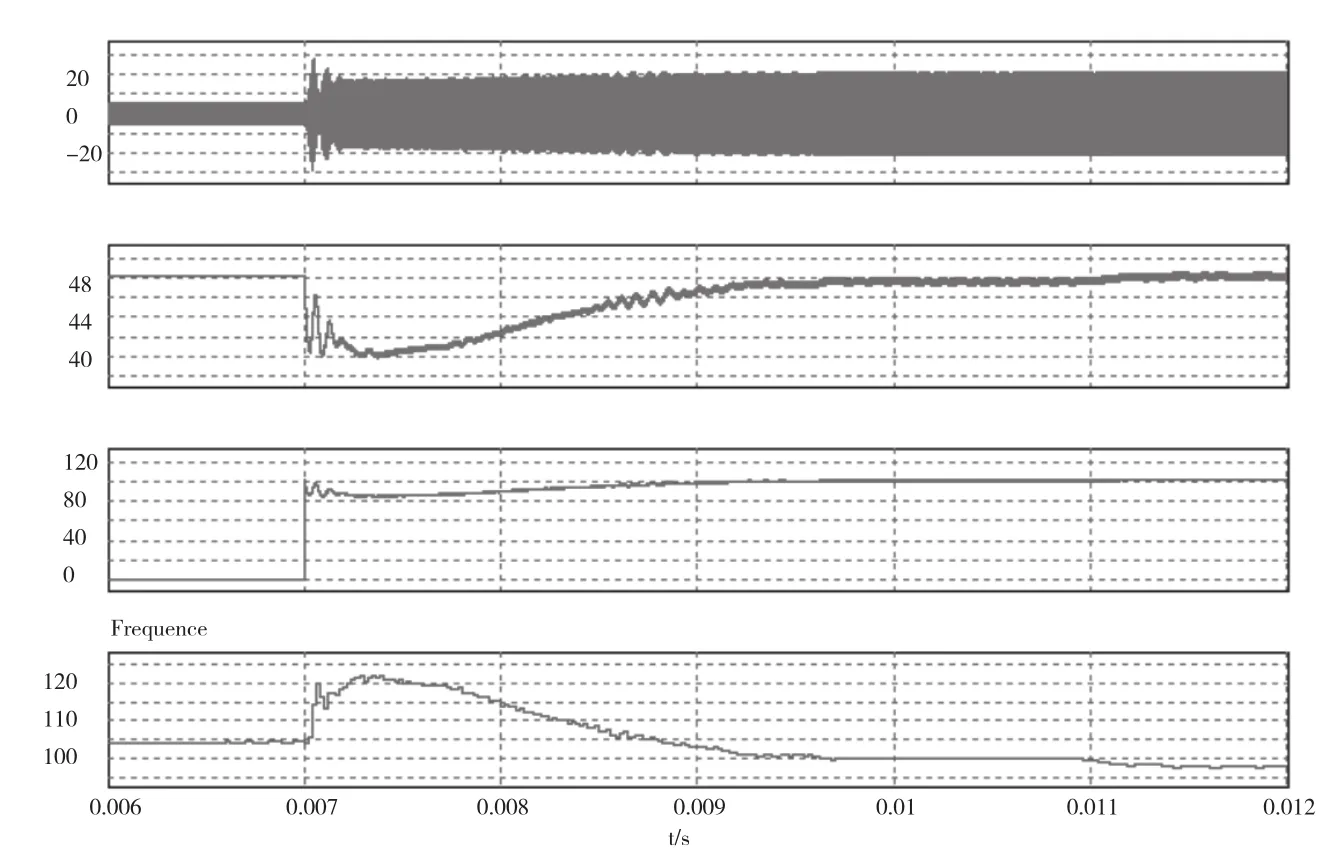
圖8 瞬間加滿載的仿真波形

6 結 論

本文對全橋LLC諧振變換器的工作原理進行了分析，利用FHA分析了LLC變換器拓撲諧振網絡的基波等效電路模型，并得出全橋LLC諧振變換器的電壓增益特性，提出了雙向全橋LLC諧振變換器的電壓環電流環雙環控制技術方案，通過對LLC諧振網絡的電流進行整流濾波采樣，得到內環電流環的反饋信號，數字控制技術將會是電源控制技術的發展趨勢。通過PSIM軟件進行仿真，仿真結果驗證了其可行性和正確性。