激光三角法測距傳感器結構設計與參數優化的研究*

樊鵬輝 楊光永 晏 婷 戈一航 徐天奇

（云南民族大學電氣信息工程學院 昆明 650000）

1 引言

目前常用于測距的方法有激光三角法、機械法、光電法和電學法等。其中，激光三角法作為一種非接觸式測量方法，具有測量速度快、可適用范圍廣、不易損傷表面、操作簡單、測量范圍大、抗干擾能力強、精度高等優點，因此在測量中得到較廣泛的使用［1～6］。由于在使用此傳感器的過程中，人們更多的關注測量精度，而對激光三角測距傳感器的光學系統、數學模型的建立、物體位移與像點位移線性輸出的設計研究較少［7～8］，本文對此問題進行了研究并提出了反射式激光三角法測量模型，推導出了測距方程、進行了參數優化、通過線性誤差補償使物體位移與像點位移線性輸出。

2 反射式激光三角測距傳感器數學模型

圖1中，在原來的三角法測量模型中加入兩個反射鏡，準直聚焦透鏡到被測面的距離為S，反射鏡（M1）與半導體激光器、反射鏡（M2）的距離分別是A1、A2，線陣CCD傳感器與反射鏡（M2）的距離是A3，激光束光軸與成像透鏡光軸之間的夾角為θ1，反射鏡（M2）、線陣CCD傳感器與水平面的夾角分別為θ2、θ3；反射鏡（M1）與（M2）的成像位移分別為Δ1、Δ2，線陣CCD傳感器上的成像位移為x；OE=y GO=L1GO′=L2。

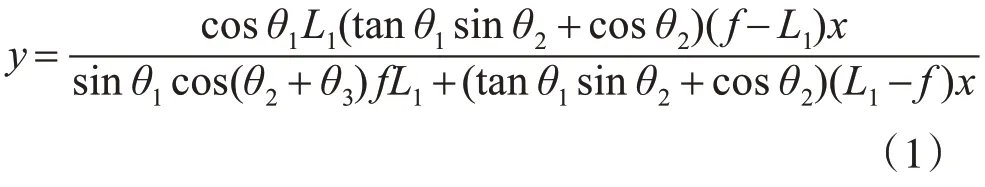
3 結構參數選取與優化

由于模型結構的參數很多，其中每個參數對系統的約束不同，因此在對模型結構設計的過程中，應能充分考慮每個結構參數對系統的影響［9］。結構參數的優化應考慮下面的兩個問題：一是要保證測量模型有足夠的分辨率和測量范圍；各參數的優化通過以下幾種情況，分別用Matlab軟件進行分析，確保成像的可靠性，夾角θ1不應取太大，不然影響成像的光強［10］，取

3.1 物距L1與放大率k和物體位移y的關系

從圖1可以看出光路設計滿足Scheimpflug條件，透鏡焦距f、反射鏡（M2）、線陣CCD傳感器與水平面的夾角分別為θ2、θ3在值不變的情況下，取、線陣CCD傳感器像元數目3648，像元間隔8μm，有效長度為29.184mm，如圖2所示；放大率k、物體位移y隨物距L1的增大而增大。

圖2 物距L1與放大率k、物體位移y、像點位移x的關系

3.2 焦距f與放大率k和物體位移y的關系

激光器的光軸與成像透鏡光軸的夾角θ1、反射鏡（M2）與水平面的夾角θ2、線陣CCD傳感器與水平面的夾角θ3不變的情況下，取L1=4000mm，如圖3所示為各參數的關系；放大率k、物體位移y隨著焦距f的增大而減小。

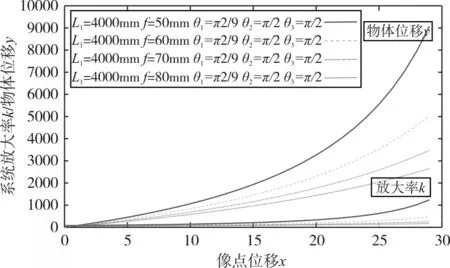
圖3 焦距f與放大率k、物體位移y、像點位移x的關系

3.3 夾角θ2與放大率k、物體位移y的關系

線陣CCD傳感器與水平面的夾角θ3不變的情況下；取L1=4000mm、f=70mm、θ1=如圖4所示；放大率k、物體位移y隨反射鏡（M2）與水平面的夾角為θ2的增大而減小。

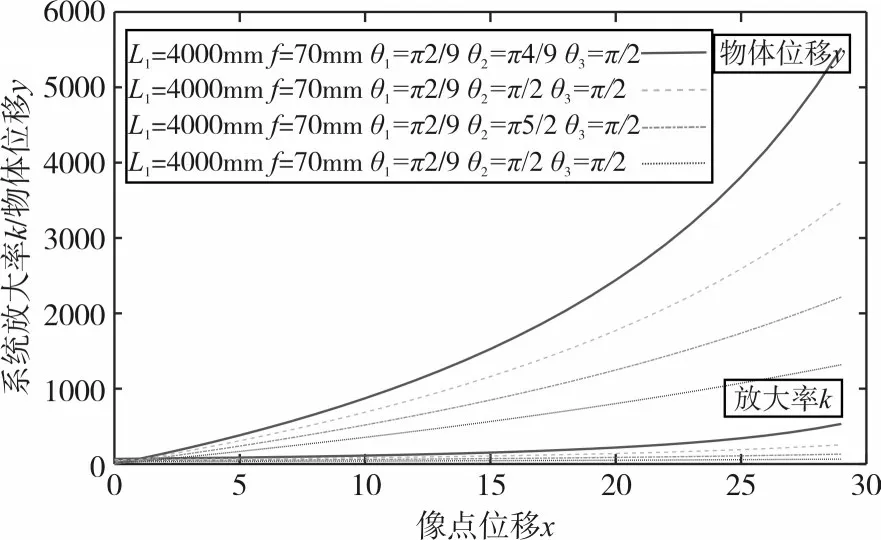
圖4 夾角θ2與放大率k、物體位移y、像點位移x的關系

3.4 夾角θ2與放大率k和物體位移y的關系

取L1=4000mm、f=70mm、如圖5所示；放大率k、物體位移y隨著線陣CCD傳感器與水平面的夾角θ3增大而增大。

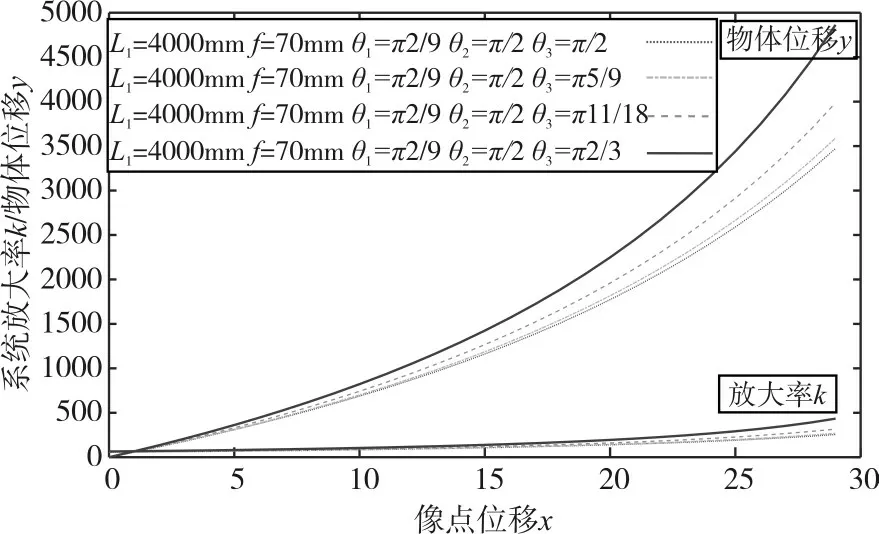
圖5 夾角θ3與放大率k和物體位移y、像點位移x的關系

以上分析了物體位移y、放大率k與入射夾角θ1、反射鏡（M2）、線陣CCD與水平面的夾角分別為θ2、θ3、透鏡物距L1、透鏡焦距f、的關系，經過對物體位移、放大率的綜合考慮，確定的最終結構參數是：激光光束與透鏡光軸的夾角；透鏡的物距L1=4000mm；透鏡焦距f=70mm；反射鏡（M2）與水平面的夾角；線陣CCD與水平面的夾角

4 曲線擬合多項式

4.1 測量數學模型建立的依據和方法

反射式激光三角法測距公式雖然在實際中不能用多項式表達出來，但根據三角法測量原理，在線陣CCD傳感器成像范圍中y（物體位移）與x（像點位移）有著一一對應的關系，沒有尖點（極限處處存在）、沒有間斷點，所以一定存在一個光滑、連續的函數y=f(x)，由泰勒定理可知，函數y=f(x)可展開為

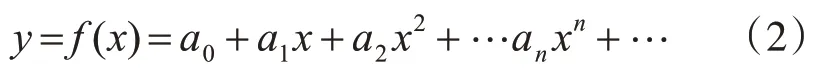
所以測量數學模型可以通過物像點的數據（xi，yi)(i=1，2，3，…，m)，擬 合 一 個n次 多 項 式pn(x)來逼近f(x)，求得一個近似解析：

4.2 最小二乘法擬合多項式

人們經常從科學的實驗數據［11～12］（xi，yi)(i=1，2，3，…，m)中，用多項式函數y=f(x)近似表達函數y=p(x)。而實驗數據中帶有一定的誤差，所以常用曲線擬合的方法對數據進行處理，其中文獻［13～14］對數據擬合進行了詳盡的分析。

在曲線擬合的方法中常采用最小二乘法擬合實驗數據，通過給定的數據集（xi，yi)(i=1，2，3，…，m)，確定系數aj使得在各個點上的偏差δi平方和達到最小。

擬合的效果越好，多項式的階數就越高，由于高階多項式的正規方程傾向于病態，計算過程易受到舍入誤差的影響，求解的系數可能不準確［15］，所以在滿足系統誤差的前提下確定多項式的最高階數。則用表1、2中的數據擬合的多項式為

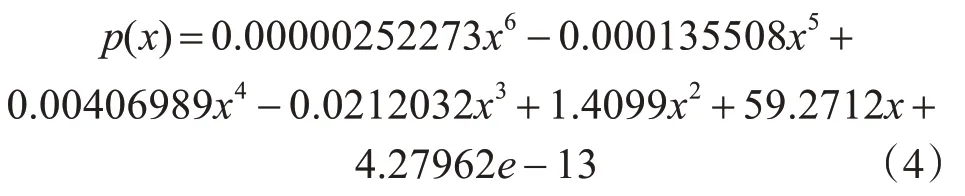
式中的4.27962e-13=4.27962×10-13。

表2中數據(xi，yi)與擬合函數p(x)的最大誤差EW=0.0032mm平均誤差E1=0.0007mm和均方根誤差E2=0.0014mm，其中6、8兩列數據沒有參與擬合多項式模型，為驗證擬合多項式的可靠性，把6、8兩列數據代入擬合后的多項式模型，則最大誤差為0.2541mm，該數值小于表1中系統誤差0.8mm，所以擬合的多項式模型滿足系統誤差的要求

表1 光學結構數據

表2 系統原始數據

5 線性誤差分析與補償

5.1 線性誤差分析

造成物體位移非線性輸出的原因是激光三角測量法相似三角形結構決定的［16～17］，是式（4）中像點位移二、三、四、五、六次項疊加的結果；經過數值分析為保證測量模型在線陣CCD傳感器上的始末兩點線性輸出，必須消掉式（4）中像點位移二、三、四、五、六次項，用線性插值法求得始末兩點的函數關系；y1=138.633261x，則線性誤差為

5.2 線性誤差補償

線性化處理是傳感器研制中重要的一環，線性化處理是提高傳感器精度、線性度、完成傳感器加工、適應計算機物體集體控制必須解決的重要問題，所以須制定相應的線性補償，則聯立式（1）、（5）和優化后的參數代入，如圖6所示。

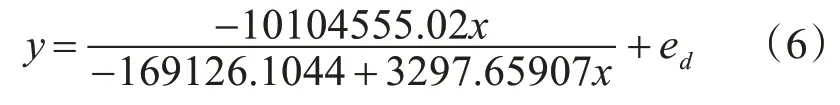
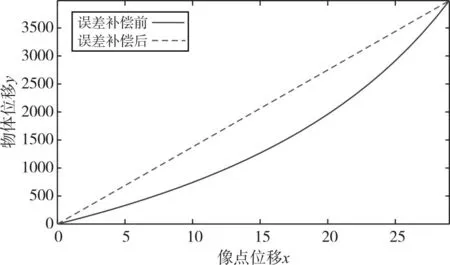
圖6 線性補償前后物體位移y和像點位移x的關系

6 結語

本文設計了反射式激光三角法測量模型并推導出原理公式，使用Matlab軟件對測量范圍、系統放大率及結構參數進行設計與優化，簡化了系統參數的設計與優化的流程，更能適應不同的待測器件和測量范圍，從而使靈活性進一步提高，進而使設計初期費用降低，最后分析了物體位移與像點位移非線性輸出的原因，并通過線性補償的方法使物體與像點位移成線性，從而提高了測量模型的線性度與精度。