耦合腔系統中Bose-Hubbard模型與穩態制備的理論研究

平一凡，楊 青，劉忠菊

（沈陽工業大學 理學院，沈陽 110870）

量子信息是量子力學與信息學相結合的交叉性學科，充當著擴展與完善經典信息的角色[1]。近年來，國內外學者以“量子編碼”為切入點，逐步擴展到對量子隱形傳態[2]、量子計算、量子度量學和量子模擬等熱點分支的研究中。從“激光冷卻和捕獲原子”到“墨子號-星地雙向糾纏”[2-3]與“遠距離量子隱形傳送”，再到2021年的九章量子模擬原型機，量子信息在實現信息傳輸更安全、計算模擬更快速和微弱測量更精密等方面已展現出廣闊的應用前景，正引領著全球的科技革命。當然，該領域飛速發展離不開量子力學和量子光學等理論體系的支撐[4-5]，如在量子信息背景下，進行量子隱形傳態實驗的前提正是建立在利用量子光學中參量下轉換非線性光學過程這一基礎之上。

量子光學與原子分子物理領域碰撞衍生出腔量子電動力學（即腔QED系統），其工作原理是將束縛在高品質腔中的原子或離子與腔中光場相互作用，從而實現量子信息處理的過程[6]。實驗中，因受較小的格點距離和較短的相干時間等因素的限制，致使很多微觀的量子現象難以觀測，腔QED系統因其優越的量子相干性，恰能有效解決這一問題，因此被用作量子模擬現象的有效平臺。另一方面，為了實現分布式量子計算[7]，以及在強關聯多體系統的研究中對多個量子比特的操控模擬，1997年Pellizzari T首次建立了耦合腔模型（即將多個分離的腔系統耦合起來）。研究發現，以玻色為媒介耦合兩光腔系統[8]可分別使被囚禁在2個腔中的原子產生糾纏及實現量子態的轉移，因此，耦合腔系統可為模擬強關聯多體系統提供有效的資源平臺。Ye等[9]提出了利用光纖耦合腔系統產生兩原子糾纏態的方案；Zheng等[10]提出了產生雙模壓縮態的方案；Zhong等[11]提出了利用兩維耦合腔系統實現多原子相干耦合的理論方案等。作為量子計算和量子模擬最具前景的物理系統之一，耦合腔系統已經成功應用于多量子體系等信息傳輸及處理中，實現了量子信息網絡化。

近年來，腔QED系統中Bose-Hubbard模型表現出空前的實用性。如耦合腔列系統的Bose-Hubbard模型展現出絕緣相到超流相的量子過程，顯示出獨特的量子特性。本文也將運用Bose-Hubbard模型，通過絕熱剔除方法得到光子的有效哈密頓，研究在兩腔耦合系統中的量子性質及穩態制備過程。

1 模型

本文選取單模光腔系統。如圖1所示，在腔內放置一個四能級原子，原子與光場發生相互作用，系統存在2種耗散情況，即原子能級躍遷可能產生自發輻射耗散，以及腔內光子也會發生泄露耗散。圖中κ為腔模的泄露率，γ為原子處于激發態的衰減率，本文后面在處理有效哈密頓時，絕熱剔除掉原子的自由度，因此，對于原子能級的衰減不予考慮了，只討論了腔模泄露對穩態輸出的影響。四能級原子具有電磁誘導透明效應，原子與腔場之間的耦合及原子的躍遷行為如下：|a>表示原子的基態，|c>為亞穩態，|b>和|d>表示原子的激發態；腔模分別與|b>?|a>與|d>?|c>之間的躍遷產生耦合，耦合系數分別為g1、g2，|c>?|b>的躍遷為經典泵浦場驅動原子的躍遷，Ω表示泵浦場的Rabi頻率，Δ和δ表示失諧量。

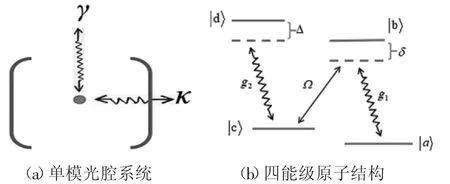
圖1 單模光腔系統示意圖與四能級原子結構圖

系統的哈密頓由自由哈密頓和相互作用哈密頓組成，在旋波近似的條件下，可以寫出該模型中系統的自由哈密頓量為

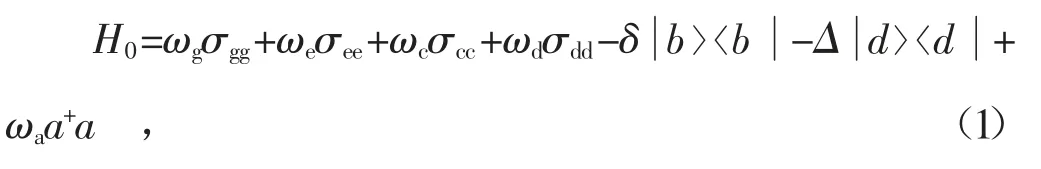
此時腔中相互作用哈密頓量可以寫作HI＝H1+H2，

其中

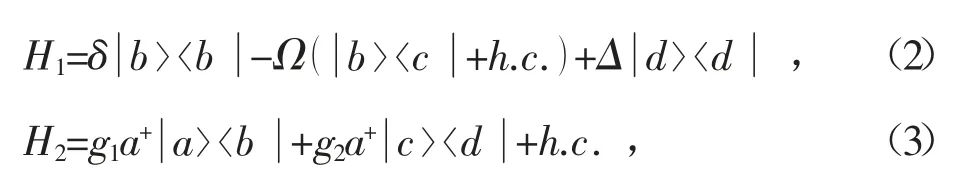
式中：a+、a表示腔場的產生、湮滅算符，在強場驅動的情況下，也就是當兩態被外場以較大的強度耦合在一起，組成了綴飾態，利用H1作用在|b>和|c>兩態上，得到綴飾態哈密頓的矩陣形式，很容易得出綴飾態H1的本征態和本征值

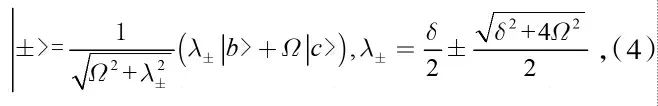
將式（4）代入到式（2）中可得

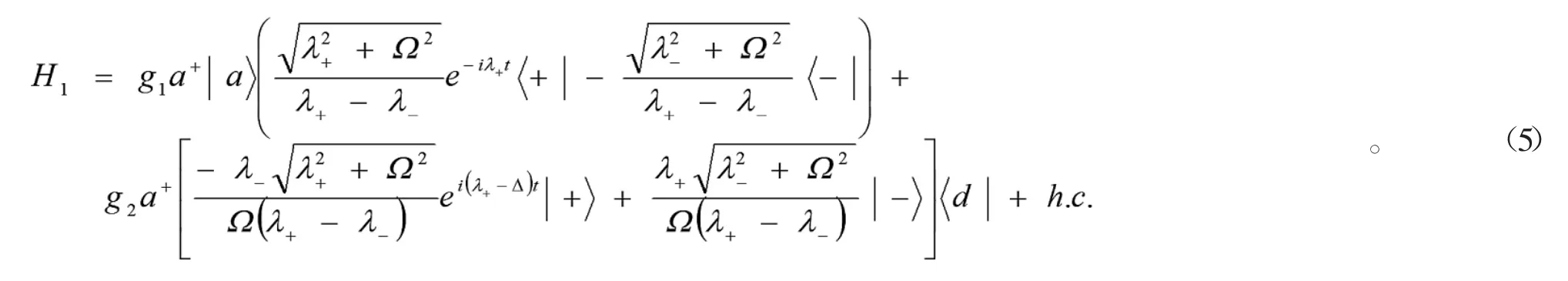
接下來，把變換后的哈密頓作幺正變換到綴飾態繪景下，即H3＝eiH1tH2e-iH1t，同時考慮＞＞g2的情況，可以利用絕熱剔除方法，將上式中的綴飾態剔除掉，得到

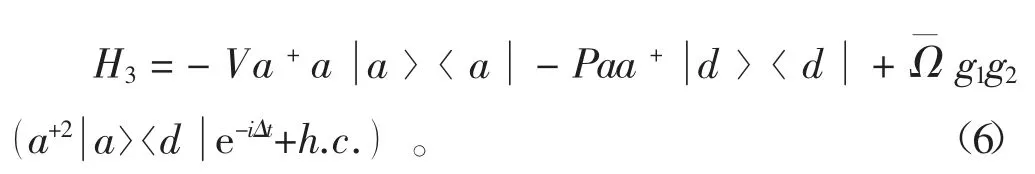
令原子的初態不處于綴飾態中的2個態上，同時觀察到式（6）中的前2項是基態和激發態的斯塔克位移，后2項則表示原子在基態和激發態之間的躍遷。因為則可以令原子的初態處于基態上，再次利用有效哈密頓的方法進行絕熱剔除掉激發態，得到最終有效哈密頓量的表達形式為

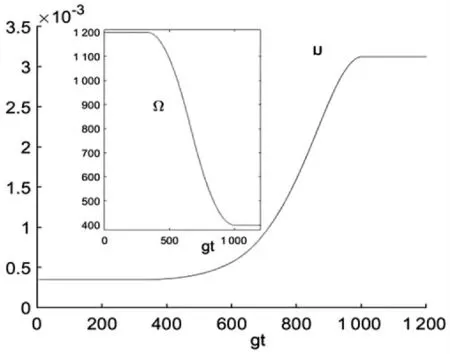
圖2 在位勢U關于經典場的變化

2 數值模擬

為了研究系統的穩態的制備，考慮兩腔耦合系統模型如圖3所示，兩腔之間的耦合通過光子的跳變來實現，J為相鄰兩腔耦合的跳變強度，同時唯象地加入2個光腔中A模光場的泄露項根據已經得出的單腔中的有效哈密頓，耦合腔系統的哈密頓可以寫為

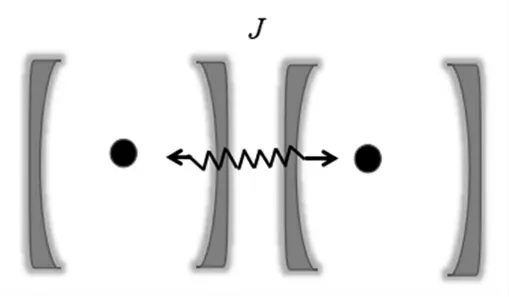
圖3 耦合腔系統。因相鄰腔光模重疊而發生光子跳變

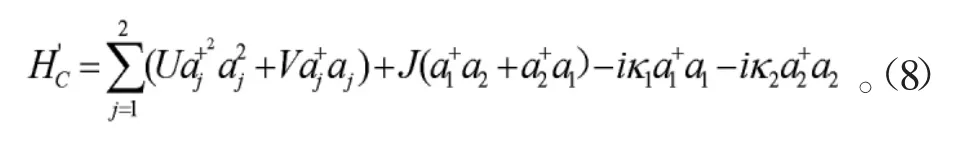
接下來，通過數值模擬來考察系統的穩態制備過程，同樣控制隨時間的變化時，系統參數Rabi頻率發生變化，通過Rabi頻率的變化，系統的平均光子數N＝。由圖4可知，實線顯示的是無耗散的情況下，平均光子數隨時間的演化，可以看出，當經典場Rabi頻率較大時，原子處于綴飾態上，光子與原子的耦合較弱，光子的行為體現再腔與腔之間的跳變。隨著Rabi頻率的減下，光子則更多參與到再單個腔內，與原子躍遷相耦合的工作中去，這正與之前討論的在位勢隨經典場Rabi頻率變化的物理過程和意義相吻合。同時，隨著時間演化，平均光子數還體現出系統從真空態項穩態的制備過程，因此，再腔經典場的驅動下，Rabi頻率越小，越能夠獲得穩態。再考慮腔場存在泄露的情況下，令κ1=κ2=κ=0.3g/0.4g/0.5g，很明顯，光腔泄露情況的存在，不但減慢了系統穩態的制備過程，同時也減小了穩態制備的保真度。

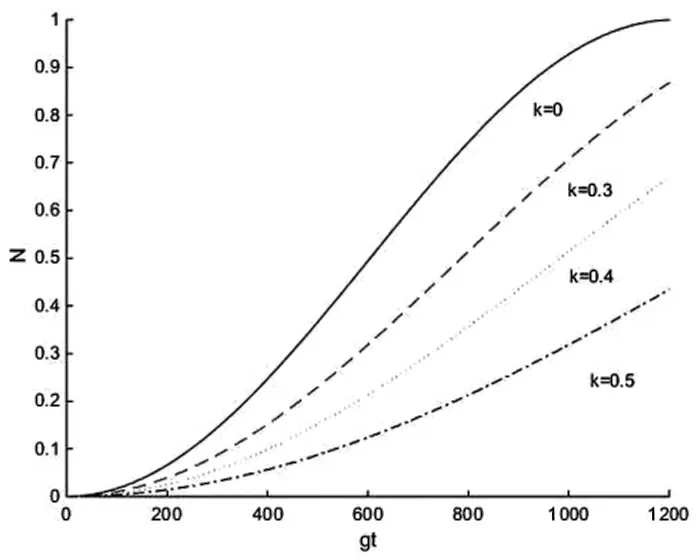
圖4 平均光子數N隨時間的變化

為了討論兩腔之間的非局域特性，接下來討論兩腔之間的量子糾纏，在耦合腔哈密頓的基態下，選用Von Neumann熵作為量子糾纏的度量，兩體之間的熵的定義式為

式中：ρA=TrB（ρAB）為系統的約化密度矩陣。

繪制了兩腔之間的基態糾纏熵關于失諧量Δ的變化圖像，如圖5所示，可以看出，當失諧量較小時，熵隨著Δ的增大而陡增，在Δ=2g附近達到最大值，然后隨著Δ的增大開始減小；同時，又改變經典場Rabi頻率為Ω，顯然，在相同失諧量Δ的狀態下，Ω越大，糾纏越大。這是由于當Ω增大時，單個光腔中的在位勢減小，光子在單個光腔中體現出較弱的非線性，也就是說單個光腔中局域性變得越來越弱，同時，光子在兩腔之間非局域行為越來越明顯，即基態糾纏熵增大。

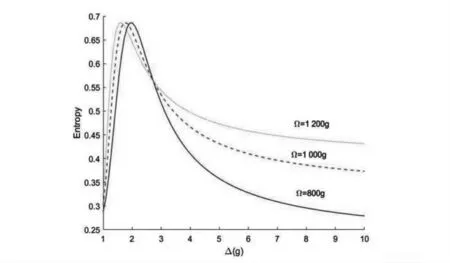
圖5 兩腔之間的糾纏熵隨失諧量Δ的變化

3 結論

本文對耦合腔QED系統進行了理論研究，在大失諧的情況下，利用絕熱剔除法，在單腔中得到關于光子的非線性有效Bose-Hubbard哈密頓量，通過對在位勢隨拉比頻率變化的研究，分析了所得哈密頓的有效性。

通過改變經典場拉比頻率進行量子操控，結果發現，令系統的初態是真空態，在拉比頻率由小變大的過程中，系統經歷了由真空態向穩態的制備過程，并分析了拉比頻率和在位勢在穩態輸出過程中扮演的角色，同時，還唯象地加入系統的耗散，觀察到腔場泄露率是影響穩態輸出的不利因素，目前高Q腔可以解決這一問題；同時又研究了兩腔之間的非局域特性，數值解析結果給出了兩腔之間基態量子糾纏何時達到最大值，并分析了經典場Rabi頻率在控制糾纏輸出中起到的作用，以上結論可以為量子信息過程提供有效的模擬平臺。