質子交換膜燃料電池活化性能快速分析方法

汪殿龍，王梓鑒*，楊代軍，程旭峰

(1.河北科技大學材料科學與工程學院，河北 石家莊 050018； 2.同濟大學汽車學院，上海 201804；3.河北科技大學機械學院，河北 石家莊 050018)

實際應用時，剛組裝的質子交換膜燃料電池(PEMFC)性能較差，為提高性能，需要使用一系列的方法來活化[1]。要確定更優的活化工藝，快速獲得電池內部關鍵位置(膜和催化劑)的電化學行為很重要。目前，此工作主要通過電化學測試方法完成，如電化學阻抗譜(EIS)、循環伏安(CV)和線性伏安掃描(LSV)法等。這些方法雖能直接反映PEMFC活化性能的變化，但存在步驟繁瑣、耗時較長等缺點，限制了PEMFC活化工藝的研究和探索。

目前，本文作者還未見到使用智能算法進行活化分析的文獻報道，但該方法在原理上與PEMFC模型優化或性能預測類似。目前使用較多的智能算法可大致分為群體智能算法、進化算法和人工神經網絡算法等3類。M.Y.Ye等[2]使用慣性權重線性下降的粒子群優化算法(PSO)優化PEMFC模型參數，并進行抗噪聲測試，認為該方法是有效的燃料電池參數識別技術，且在一定的測量噪聲下，依然表現良好。Y.Cao等[3]在海鷗優化算法(SOA)中加入萊維飛行(個體移動步長較大概率出現大跨度步長)機制，以加快算法的收斂速度。在同一種電池系統上，優化后的算法經22次迭代后的誤差平方和(SSE)為2.18，而標準SOA經80次迭代后的SSE為2.21，優化后的算法在求解質量和收斂速度方面有明顯提升。U.K.Chakraborty等[4]使用改進的差分進化(DE)算法優化PEMFC參數，在高低噪音下的結果顯示，相比幾種標準DE變體和遺傳(GA)算法，改進DE算法在500 000次迭代后的適應度值、達到目標適應度的迭代次數和運行時間等3個方面至少有一個優于其他幾種算法。T.Wilberforce等[5]使用改進的人工神經網絡(ANN)算法擬合PEMFC的極化曲線，并預測性能，使用的兩種神經網絡模型雖然有差異，但都能取得相對滿意的結果。上述算法中，群體智能算法的收斂速度較快，但存在解精度低、容易陷入局部最優的缺點，解的一致性較差[6]；人工神經網絡通常需要大量的數據和高成本的計算。這些缺點在一定程度上限制了群體智能算法和人工神經網絡在PEMFC活化分析中的應用。綜上所述，DE算法更符合分析方法的要求。

為減少PEMFC關鍵位置電化學行為的獲取時間，快速獲得有關PEMFC活化狀態及有效性的信息，本文作者提出一種基于智能算法的快速分析方法，利用DE算法進行PEMFC活化的快速性能分析。首先進行PEMFC的活化實驗，再分析相關的實驗結果，最后驗證該方法的可行性。

1 快速分析方法

活化性能快速分析方法的結構見圖1。

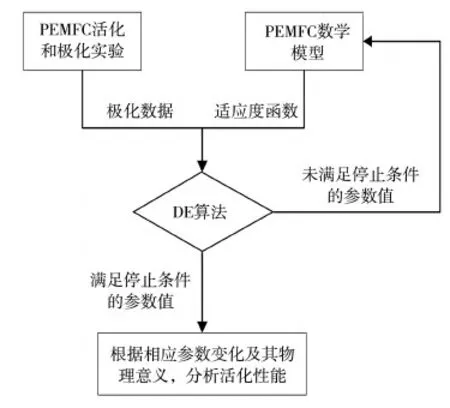
圖1 快速分析方法的結構圖

該方法需要一個PEMFC模型、DE算法和不同活化時間節點的極化數據。通過PEMFC的活化和極化實驗，得到極化數據，再利用DE算法和PEMFC模型分析不同活化時間節點的極化數據，最終得到活化性能。

1.1 PEMFC模型

PEMFC常用的數學模型見式(1)。

Ucell=E0-ηohm-ηact-ηconc

(1)

式(1)中：Ucell為電池電壓；ηohm、ηact和ηconc為當電池有負載時的3個電壓損失，即歐姆損失、活化損失和濃差損失；E0為開路電壓。

1.1.1 歐姆損失ηohm

PEMFC的歐姆損失ηohm包括電流穿過雙極板及外部總線的電子電阻和膜對離子流的離子電阻。

由于活化過程中電子電阻幾乎不發生變化，可將ηohm的等效電阻用面積比電阻r表示，以反映膜的變化。ηohm與電流密度J的關系見式(2)。

ηohm=J·r

(2)

1.1.2 活化損失ηact

電極上發生反應所需要的能量體現為部分電壓損失，即活化損失，主要集中在低電流區域。

活化極化損失方程通常由塔菲爾方程推導出，見式(3)。

(3)

式(3)中：A為塔菲爾斜率；J0為交換電流密度，可作為判斷電化學反應催化劑活性的指標。

1.1.3 濃差損失ηconc

電池電流較大時，電極附近的反應物濃度低于入口濃度，會造成部分電壓損失，即濃差損失。通過能斯特方程和菲克擴散定律，可得到濃差極化的電壓損耗關系，見式(4)。

(4)

式(4)中：B為濃差損失常數；JL為當燃料以最大速度供應時，燃料電池所能達到的極限電流密度。

1.1.4 目標函數

PEMFC的極化曲線是常用的穩態性能指標，通常由即時測量隨電流變化的電池電壓得到。

通過DE算法來最優搜索PEMFC數學模型的參數，目標函數見式(5)。

(5)

式(5)中：N為數據數量；Up(m)為PEMFC模型所得到的第m個模型的電壓；Udata(m)為每次活化循環后極化實驗的第m個實驗數據。Up由式(1)計算，使用6個差分進化參數(A、J0、JL、E0、B和r)。

1.2 差分進化(DE)算法

DE算法的原理，是從設定邊界中隨機產生種群開始，在優勝劣汰的規則下，通過不斷地迭代進化，引導搜索過程向全局最優值逼近。對于PEMFC的參數最優搜索問題，適應度函數即為目標函數式(5)，目標函數的值越小，個體的適應度越好。用于本策略的DE算法可描述為以下步驟。

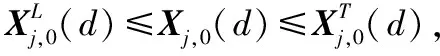
(6)

步驟②：變異。變異操作有多個版本，實驗調用的特定版本是DE/rand/1/bin，即隨機選擇3個不同的個體(用p1≠p2≠p3表示不同)，將其中任意兩個向量的差值進行縮放并與另一向量求和，產生變異個體Hj,G+1，見式(7)。

Hj,G+1=Vj,0(p1)+F·[Vj,0(p2)-Vj,0(p3)]

(7)

式(7)中：F為縮放因子；G為當前進化代數。

變異過程中要判斷變異后的個體是否滿足邊界條件，若不滿足，需要再次隨機生成(同步驟①)。F的取值會影響結果，當取值較小時，種群之間的差異度小，容易出現“早熟”現象(早期某一個體適應值大幅超過平均個體適應值)。為避免“早熟”現象，加入具有自適應特性的變異算子[7]，自適應算法見式(8)、(9)。

(8)

F=F0·2λ

(9)

式(8)-(9)中：λ為中間變量；F0為變異算子；Gm代表最大進化代數；e為自然常數。自適應算法使F在進化初期值較大，可避免過早收斂，保持種群多樣性；隨著進化進行，F逐漸變小，在后期接近F0，保留最優信息，增加全局最優收斂的概率。

步驟③：交叉。在變異后的個體Hj,G+1和初始個體Vj,G中，任意選擇“染色體”中的“基因”(個體向量中的某一解)組合成新的個體Kj,G+1，如式(10)所示，其中Cr表示交叉概率。為確保變異個體向量至少有一個“基因”能傳給下一代，交叉操作的初始是在變異個體中隨機選取第drand位“基因”，作為交叉后新個體的第drand位“基因”。

(10)

步驟④：選擇。DE算法的選擇操作使用貪婪算法，將當前向量與初始向量的適應度進行比較，總是選適應度最優的那個向量個體，見式(11)。此處選擇結果取決于適應度函數式(5)。

(11)

步驟⑤：轉到步驟②，重復迭代，直到滿足停止條件。

DE算法的停止條件，通常是設置最大迭代次數或適應度小于設定值。

2 實驗

實驗裝置包括G20實驗平臺(Greenlight公司)和自制0.1 V/300 A可控電子負載。膜電極組件(MEA)G1.0-35B(河南產)由M735.18質子交換膜、催化劑層(CL)和氣體擴散層(GDL)組成，詳細參數見表1。MEA放置在兩個有蜿蜒氣體通道的石墨板中間，然后壓在兩塊鍍金銅板之間，GDL由碳紙制成。G20實驗平臺設有反應物氣體的加熱加濕系統和電池的溫控器。采用一系列的脈沖電流進行活化，設定脈沖電流周期為10 s，占空比為20%，電流形式見圖2。活化實驗條件如下：陰、陽極壓力分別為120 kPa、140 kPa，電池溫度為85 ℃，陰陽極相對濕度均為80%。

表1 MEA的詳細參數

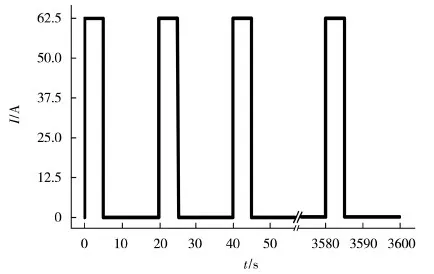
圖2 PEMFC活化脈沖電流波形

實驗只考慮脈沖電流活化對燃料電池性能的影響。活化后，燃料電池停止工作并冷卻。隨后進行極化測試，測試條件如下：電池溫度為75 ℃，露點溫度為60 ℃，陰、陽極壓力分別為80 kPa、100 kPa，氣體相對濕度為50%，氫/空氣的化學計量比為1.7/3.0。在不同的活化時間點，連續測量PEMFC的電流和電壓，得到一系列極化曲線。

EIS測試在Reference 3000電化學工作站(美國產)上進行，交流信號振幅為工作電流的5%。EIS測試在每次極化測試之后進行，電池操作條件與極化測試一致。基于EIS結果，由等效電路模型擬合可獲得歐姆阻抗Rohm、電荷轉移阻抗Rct和傳質阻抗Rmt，恒相位元件CPE主要描述雙層電容的行為，電荷傳輸和質量傳輸分別對應一個雙層電容，即CPEct和CPEmt。CPE包括兩個參數，CPE-P表示原件特性偏離純電容的程度，當取值為1時，恒相位原件等效為電容；CPE-T可表示等效電容的大小。EIS的測試數據通過Zview軟件進行等效電路模型分析，等效電路模型如圖3所示。

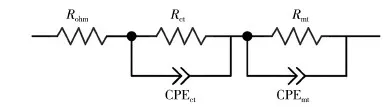
圖3 EIS分析的等效電路模型

3 結果與討論

采用活化過程中不同時間點的極化實驗數據，評價DE算法的識別能力。比較活化初始、活化后1 h和活化后2 h電池的優化參數值，來分析活化的機理，并從擬合后J-U曲線的形狀、適應度值和EIS測試，評價所提方法的有效性。

DE算法中的控制變量設置為種群大小Np=70，交叉概率Cr=0.8和最大進化次數5 000次。縮放因子F由自適應的變異算子得到，設定變異算子F0=0.5。算法參數的設定與文獻[4]的推薦值相同，參數的大小與實際問題無關。每個DE種群表示一組燃料電池參數，模型參數的搜索范圍根據物理意義來設置。DE算法通過MATLAB軟件實現。

活化初始、活化1 h及活化2 h后PEMFC的極化曲線和功率密度曲線如圖4所示。

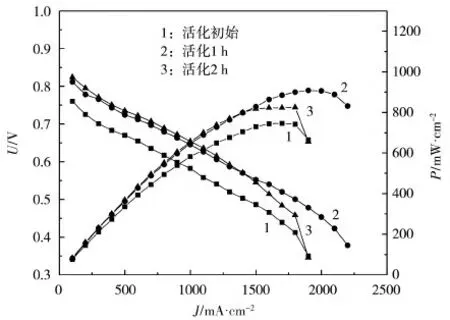
圖4 極化曲線和功率密度曲線

從圖4可知，當電流密度大于1 700 mA/cm2時，PEMFC的性能相對不穩定，主要原因是陰極側產生大量的水。活化1 h后，PEMFC的最大功率密度提升了21.7%。

不同活化時間節點DE算法的收斂過程見圖5，DE算法識別結果見表2。從表2可知，活化1 h后，與活化初始相比，E0、J0、B和JL增加，r、A減小。當在不同的活化時間點下達到最大進化次數時，DE算法可得到一個較小的目標函數值Ffit，且均小于5.5×10-3，說明使用DE算法對實驗數據進行參數搜索是可行的。從這些參數的物理意義可判斷，脈沖電流能通過提高催化劑的活性和膜的滲透率，降低膜的離子阻抗，減少3個極化區域的電壓損失。比較活化1 h和2 h的參數變化可知，r繼續減小，原因是膜的離子阻抗通常是膜中含水量的函數，表明膜的水化程度隨活化而增加。實驗發現A增加、J0減小，表明活化損失增加，與傳統觀點不同，且在文獻[8]中已有報道。可變電流的活化被認為可在催化劑層上形成孔隙，特別是隨著電流的增加，孔隙將逐漸滲透到內部。氫分子很容易通過孔隙，不容易被Pt/C粒子捕獲，暗示了電化學活性面積減小，即活化損失增加[8]。此外，實驗還發現B增加、JL減小，表明過度活化可能使濃差損失增加。

圖5 不同活化時間節點DE算法的收斂過程

表2 DE算法識別結果 Table 2 Recognition results of DE algorithm

實驗數據與從DE優化模型中得到的J-U特性之間的比較如圖6所示。

從圖6可知，雖然實驗數據與DE算法優化模型存在一定的誤差，但擬合效果可以接受。

圖6 DE算法優化模型與實驗數據的比較

實驗主要通過EIS測試驗證DE算法最優搜索結果的有效性。由于是在不同條件下得到的結果，EIS和算法分析數據不能直接進行定量比較，但可通過相關參數的變化定性驗證。利用DE算法進行基于實驗數據的參數搜索的任何進展都非常重要，原因是有利于識別結果更加接近實際值。

圖7為800 mA/cm2下不同活化時間點的奈奎斯特圖。

圖7中的曲線都由高頻區域和低頻區域的兩個弧組成。高頻區域(靠近虛軸)的弧通常與MEA中的電荷動力學有關，低頻區域(遠離虛軸)的弧通常與氧傳質阻抗有關。活化在1 h后基本完成，因為此時高低頻圓弧半徑均最小，即電荷轉移阻抗和氧傳質阻抗均最小。

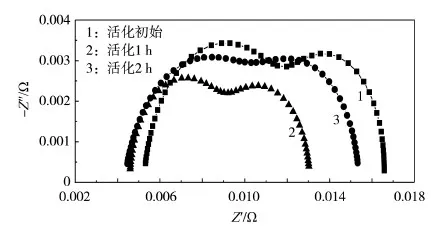
圖7 800 mA/cm2下不同活化時間點的奈奎斯特圖

等效電路的擬合結果詳見表3。

從表3可知，PEMFC的Rohm、Rct和Rmt在活化1 h后達到一個較小值，表明脈沖電流活化方法可從3個極化區降低PEMFC的電壓損失。在活化2 h后，Rohm繼續下降，但Rmt和Rct增加。這表明，一方面電池的活化時間越長，膜的水化程度越高；另一方面，挖掘效應阻礙了Pt/C粒子捕獲氫分子，且長期高溫高壓活化使電池內部壓力加大，阻礙了氧的傳質，導致較高的活化損失和濃差損失[9]。在耗時方面，極化測試在活化研究中幾乎是必要的，因此不予考慮。

表3 不同活化時間點等效電路的擬合結果 Table 3 Fitting results of equivalent circuits at different activation time points

EIS與基于DE算法的快速方法的結果比較見表4。

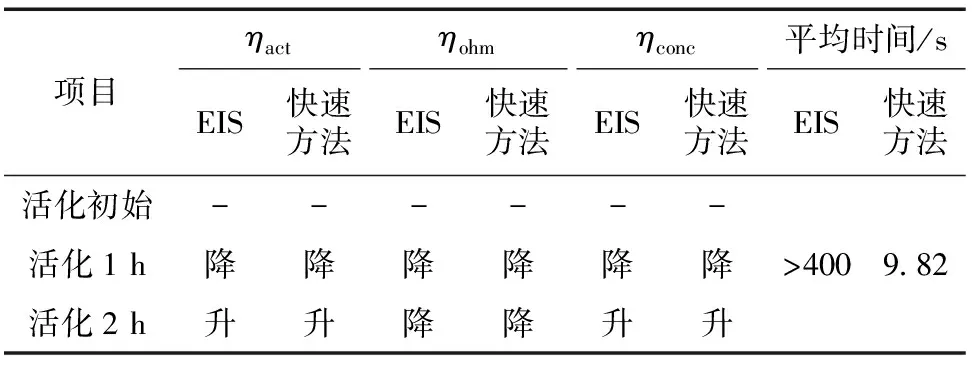
表4 EIS與基于DE算法的快速方法的結果比較

從表4可知，基于DE算法的快速方法比EIS測試約快40倍。另外，EIS分析結果與算法分析得到的結果一致，驗證了所提出的基于DE算法的PEMFC快速活化性能分析方法具有一定的可行性。

4 結論

本文作者提出一種PEMFC活化性能快速分析方法，并通過實際活化實驗及EIS測試，驗證該方法的可行性。

實驗結果表明，活化1 h后，MEA在活化損失、歐姆損失和濃差損失等方面降低了相應的電壓損失。長時間的活化對燃料電池有負面影響，雖然很難在極化曲線中體現，但算法結果和EIS分析均說明，長時間活化后，盡管歐姆損失仍減少，但濃差損失和活化損失增加。此外，常用的燃料電池測試方法繁瑣且耗時較長，而該方法僅在10 s內通過J-U曲線快速分析燃料電池，結果質量較高，很適合活化性能的初步評估，有利于快速確定更好的活化工藝及參數。