基于改進FA算法的河流突發水污染事件溯源①

趙棟梁,周曉磊,竇志強,武 暕

1(中國科學院大學,北京 100049)

2(中國科學院 沈陽計算技術研究所,沈陽 110168)

3(遼寧省生態環境監測中心,沈陽 110161)

河流突發水污染事件會對河流下游區域的生態系統造成破壞,并且隨污染排放時間增加,污染擴散面積逐漸擴大,對人民群眾以及生態環境的影響逐漸加大,因此河流突發水污染事件的第一要素是確定污染源位置[1].本文主要通過研究污染物在河流中的擴散規律,并通過監測站所觀測到的污染物濃度變化對污染物排放的位置、時間、質量進行溯源[2],從而還原污染物排放的變化過程,研究的難點在于污染源溯源求解過程中的求解不唯一、污染源溯源相關的水文參數測量階段存在誤差,污染物回溯模型參數設置存在誤差,并且污染物的傳播過程不能通過實驗來重復[3].

水污染溯源的方法最初來自于空氣污染的溯源,最開始被應用于地下水污染的研究[4],Alapati 等[5]通過最小二乘法結合一維地下水擴散模型研究了的地下水污染源參數,國內的白玉堃等[6]通過卡爾曼濾波方法溯源地下水的污染源個數和位置,張雙圣等[7]采用貝葉斯公式結合二維水質的對流模型研究了地下水的污染源瞬時排放模式.在河流污染中也采用了和學者研究地下水污染中類似的方法[8],國內外學者在對河流污染的污染源排放相關參數的求解做了大量的工作,大致可以把研究分為3 大類,分別為數學分析法、模擬優化法、概率分析法,其中,前2 個稱為確定性方法,最后1 個稱為不確定性方法.

在數學分析法的研究上,辛小康等[9]通過遺傳算法和數學分析方法相結合,通過一維水質模型研究了單點源和多點源的瞬時污染源參數識別問題; 饒清華等[10]通過有限元法研究了閩江下游不同地點的污染物濃度情況.在模擬優化法上,劉潔等[11]通過遺傳算法在一維對流擴散方程求解目標函數; 吳一亞等[12]通過微分進化算法求解寬淺河道瞬時污染排放遷移問題.確定性方法通過污染物濃度數據反推污染源參數,但是當數據出現一點偏差時通過確定性方法求解結果偏差較大.

在概率分析法的研究上,陳海洋等[13]通過貝葉斯推理和二維水體擴散規律構建模型,并通過馬爾科夫鏈蒙特卡羅法求解污染源相關參數; 程偉平等[2]通過逆向概率密度法求解了一維水質的污染源參數識別問題; 王家彪等[14]通過結合正向位置概率密度和逆向位置概率密度之間的耦合關系建立求解模型,并通過微分進化算法求解模型,能夠實現求解參數之間的解耦,降低時間復雜度,并且結合了確定性和不確定性分析方法,一定程度上降低了參數誤差造成的影響.概率分析方法在一定程度上能夠避免參數誤差造成的誤差較大,但是受觀測誤差影響比較大,具有一定的隨機性.

上述研究中,污染物濃度監測數據使用所有監測站點不同時刻的數據,不同監測站間數據沒有做區分,但實際河流中,污染物濃度也存在水流和污染物混合不均勻導致監測濃度不準確現象,監測站的數據可以分為不準確、相對準確兩種數據類型.基于大部分監測站點的數據都是相對準確的事實,本文提出一種基于多螢火蟲種群的求解方法,通過在算法初期隔離不同監測站間的數據來避免不準確數據使相對準確數據失真,在算法后期通過不同種群間相互作用通過多數效應來淘汰不準確數據類型的種群,從而避免某個監測站數據不準確對求解造成的系統誤差.

本文采用耦合概率密度方法對所需求解的參數進行建模[14],并考慮到觀測誤差和一維水質模型需要污染物混合均勻條件,代入實時的水文特征,采用改進的螢火蟲算法(firefly algorithm,FA)算法,引入多種群機制將多個污染物監測站數據同時代入求解,改進后的算法具有更強的全局搜索能力和跳出局部極值能力,對建模后的目標函數進行求解,尋找污染源排放相關的排放位置、排放時間、排放強度.

1 水動力模型構建

河流水污染問題主要是通過已知的水文參數、監測站監測數據信息對污染物的溯源需要根據具體河道的水文特征進行水動力學模型構建,利用污染物在水流中的正向質量概率密度和逆向質量概率密度之間的耦合概率密度關系,使污染物排放強度與排放位置和排放時間之間解耦.

1.1 污染源擴散關系

對于污染物的排放問題,污染物進入河流后的擴散規律滿足質量守恒定律[15],可表示為:

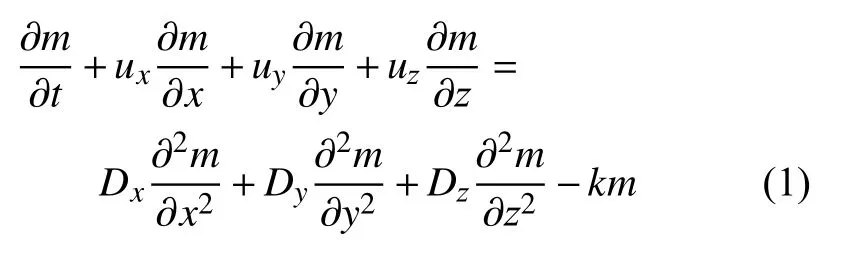
其中,m為河道內點(x,y,z)在t時刻污染物的濃度,單位mg/L;t為污染物排放后的時間,單位s;Dx、Dy、Dz分別為河流長度方向、寬度方向、深度方向的彌散系數,單位m2/s;ux、uy、uz分別為河流長度方向、寬度方向、深度方向的水流的平均流速,單位m/s;k為污染物的降解系數,單位s-1.

對于內陸河流,污染物擴散主要受河流兩岸和河流底部的約束,因此污染物在水流中會產生邊界反射,水中對流、擴散、吸附等現象.考慮到河流寬度和河流深度遠小于河流長度,在非洪訊期,水流速度基本不變,污染物在被投放到河流內后,能在投放點斷面附近迅速擴散,擴散后斷面附近污染物濃度基本相同.因此可以把污染源在內河擴散問題簡化為一維水體擴散模型,排入河流后的污染物濃度隨時間和位置的變化情況可忽略y,z方向上的變化[16],將式(1)簡化為:

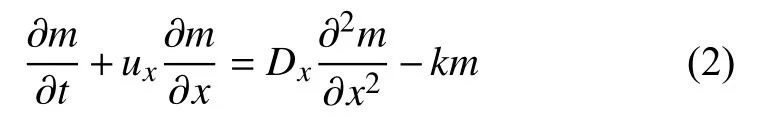
若污染物為瞬時排放模式,則可對式(2)進行傅里葉變換[17],可以得到t時刻在x斷面處的污染物濃度關系式:

其中,m(x,t)表示污染物在河道x位置時間為t時刻斷面的污染物濃度,單位g /L;M為污染物排放處的強度,單位g/m2;t0表示污染物的排放時間;x0表示污染物的排放位置.

由式(3)可知,對于河流突發水污染事件溯源問題,需要確定污染物排放處強度M,污染物排放位置x0,污染物排放時間t0.溯源問題相對于模擬過程具有不能直接求解的特點,但是可以通過監測站的斷面信息確定污染源3 個參數的約束范圍,然后通過迭代試算尋找最優的參數組合.但是3 個未知數的組合復雜度較高,尋優過程具有運算量大,求解偏差大,求解時間長的特點,因此需要引入降維方法,降低模型的維度.

本文利用正向位置濃度概率密度(從污染源排放斷面判斷污染源出現在下游的濃度分布情況)和逆向位置濃度概率密度(從監測斷面判斷污染源在不同斷面處的可能性大小)的關系[14],將求解污染源的濃度分布問題轉化為求解污染源的逆向位置濃度概率問題,從而將x0、t0的求解和M分開.

1.2 逆向位置關系

設m(xs,xob,t)表示的監測濃度對應的正向位置濃度概率密度為m1(xs,xob,t),逆向位置濃度概率密度為m2(xs,xob,ts),根據文獻[2]可知,它們之間存在以下關系:

其中,xs為污染源位置,xob為觀測斷面位置,t為污染物正向移動的時間點,ts為通過觀測斷面溯源計算的污染源排放時間點;m(xs,xob,t)表示時間為t時,污染源從排放斷面xs擴散到xob觀測斷面的濃度;m1(xs,xob,t)為污染源從排放斷面xs擴散到xob觀測斷面t時刻觀測斷面的正向位置濃度概率密度,量綱為m-1;m2(xs,xob,ts)為從觀測斷面xob推測出污染源在ts時刻處在xs處的逆向位置濃度概率密度,量綱為m-1.

由式(4)、式(5)可知,正向位置濃度概率密度和逆向位置濃度概率密度兩者在計算中具有高度耦合性,在同一位置,計算方向不同,計算結果概率密度相同[18].因此可以得出:

由于m2(xs,xob,ts)具有m-1的量綱,因此也滿足式(2),對其也進行傅里葉變換得到逆向位置濃度概率密度為[19]:

由式(7)可知,污染源的逆向位置濃度概率與污染物排放強度無關,可以通過求解m2(xs,xob,ts)來計算排放位置x0,排放時間t0.

2 溯源優化模型構建

2.1 位置時間模型

由式(4)可知,m2(xs,xob,ts)和m(xs,xob,t)之間具有線性相關性,相關系數為污染物排放濃度的倒數.設mi(i=1,2,3,…,n)為一系列觀測斷面濃度數據,mi2(i=1,2,3,…,n)為一系列與mi相對于的通過觀測斷面xob確定的逆向位置濃度概率密度[20].兩者相關系數為R(R≤1),R值越接近1 代表此時逆向位置濃度概率密度越接近真實值,可知其有以下相關性:

其中,n為觀測斷面濃度數據和對應的逆向位置濃度概率密度數據的個數,表示觀測斷面濃度數據的平均值,表示逆向位置濃度概率密度數據的平均值.

設x0,t0為真實的污染源排放位置和排放時間,優化求解的目標是尋找最接近真實值的組合.因此將溯源問題轉化求解最優的x′,t′組合使當前的相關系數R最接近1,可通過求解以下目標函數完成求解[20].

目標函數的約束條件是通過已有的監測站斷面數據確定的排放位置的范圍和排放時間的范圍:

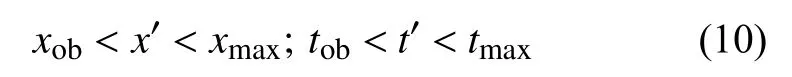
通過求解式(9),尋找其最小值即可得到最近接近x0,t0的x′,t′組合.

2.2 污染物排放強度模型

通過位置時間模型求得的x′,t′組合,可以作為污染源排放量模型的已知條件,因此污染源排放量模型只需要求解污染物排放處的強度M這一個未知參數,根據文獻[20]可知,污染物的正向位置濃度概率密度和逆向位置濃度概率密度具有線性相關性,可得式(11):

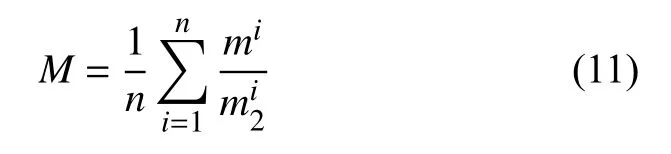
可以通過式(11)估算污染物排放處的強度M的大小范圍作為約束范圍.

為了進一步確定M的大小,可以通過正向位置濃度概率密度構建目標函數:

目標函數中M的約束范圍由式(11)確定的范圍確定:

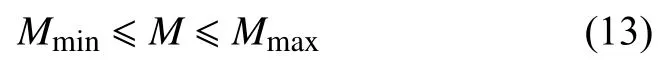
通過求解式(12),尋找其最小值即可得到最接近真實值的污染物排放處的強度M.

3 溯源優化模型求解

在第2 節將污染物溯源需要求解的污染物排放位置x0,污染物排放時間t0,污染物排放強度M三個參數轉化為對式(9)、式(12)兩個目標函數求最小值問題,本文選用改進的螢火蟲算法[21]求解目標函數,為了使算法更適合河流污染溯源的求解,做了以下改進.

3.1 改進參數控制策略和約束條件

在原始的螢火蟲算法中,控制隨機擾動的步長 α是一個固定值,主要目的是作為隨機擾動項增加算法的搜索能力和一定程度上保持種群多樣性.α越大,全局搜索能力越強,但是算法后期可能存在跳過最優解,發生在最優解附近震蕩的現象; α越小,局部搜索能力越強.

對應到本問題,在求解目標函數式(7)時,污染物排放位置x的范圍相對于污染物排放時間范圍較大,因此需要提供一個縮放系數k,來調整不同維度的步長相對值,可表示為:

其中,ki(i=1,…,d),分別表示在1 到d維的縮放因子,大小由不同維度之間的搜索范圍比例確定,α0為控制隨機擾動的步長初始值,大小為[0,1].

由于污染物溯源問題在初期搜索范圍較大需要更大的步長來加快搜索速度和全局搜索能力,在后期需要較小的步長來提升搜索精度,因此針對本問題參考文獻[21]提出一種自適應步長改進策略,可表示為:

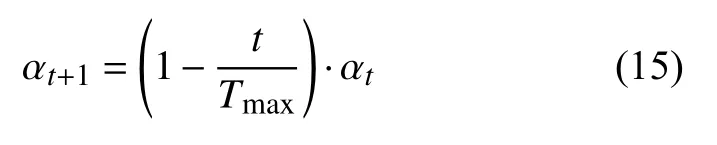
其中,t(t=1,…,n)表示當前的迭代次數,αt表示第t次迭代時隨機擾動的步長大小,Tmax表示迭代次數的最大值.

原始的螢火蟲算法在移動位置時沒有考慮在該維度的搜索范圍,對應到污染物溯源問題上,x0,t0,M三個參數都可以通過監測站的參數和河道信息確定其大致范圍,因此需要對螢火蟲的移動范圍做出限制[16],可表示為:

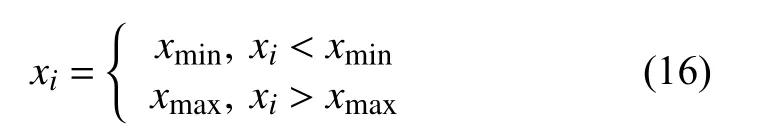
其中,xmin表示在該維度搜索范圍的最小值.xmax表示在該維度搜索范圍的最大值,xi表示第i只螢火蟲的位置.

3.2 改進種群策略

原始的螢火蟲算法中,螢火蟲亮度較高的個體只會對其附近的亮度相對較低的個體有吸引力,但是對距離較遠的螢火蟲個體沒有吸引力,因此原始算法容易陷入局部極值過早收斂導致求解誤差較大.針對上述問題本文參考文獻[22]提出的多螢火蟲種群的優化策略改進算法,具體內容見第3.3 節算法流程中步驟3-11.

3.3 算法流程

對于污染物溯源問題,早期的學者采用耦合概率密度分析方法建模求解時,沒有區分不同監測站的污染物濃度數據,某個監測站的監測值可能因為污染物和河流混合不均勻或者某個設備本身存在系統誤差,從而導致通過該監測站數據求解誤差較大.

針對本問題提出如下改進: 首先監測站間數據相互獨立,使用單個監測站數據依次使用多種群螢火蟲算法求解,最后分析各個監測站的求解結果,采用標準差分析法,若通過某一個監測站求解的結果相對于其他使用其他監測站數據求解結果偏差較大,證明該監測站數據為不準確數據,淘汰該結果[23].整體算法結構如圖1 所示,具體算法流程如下.

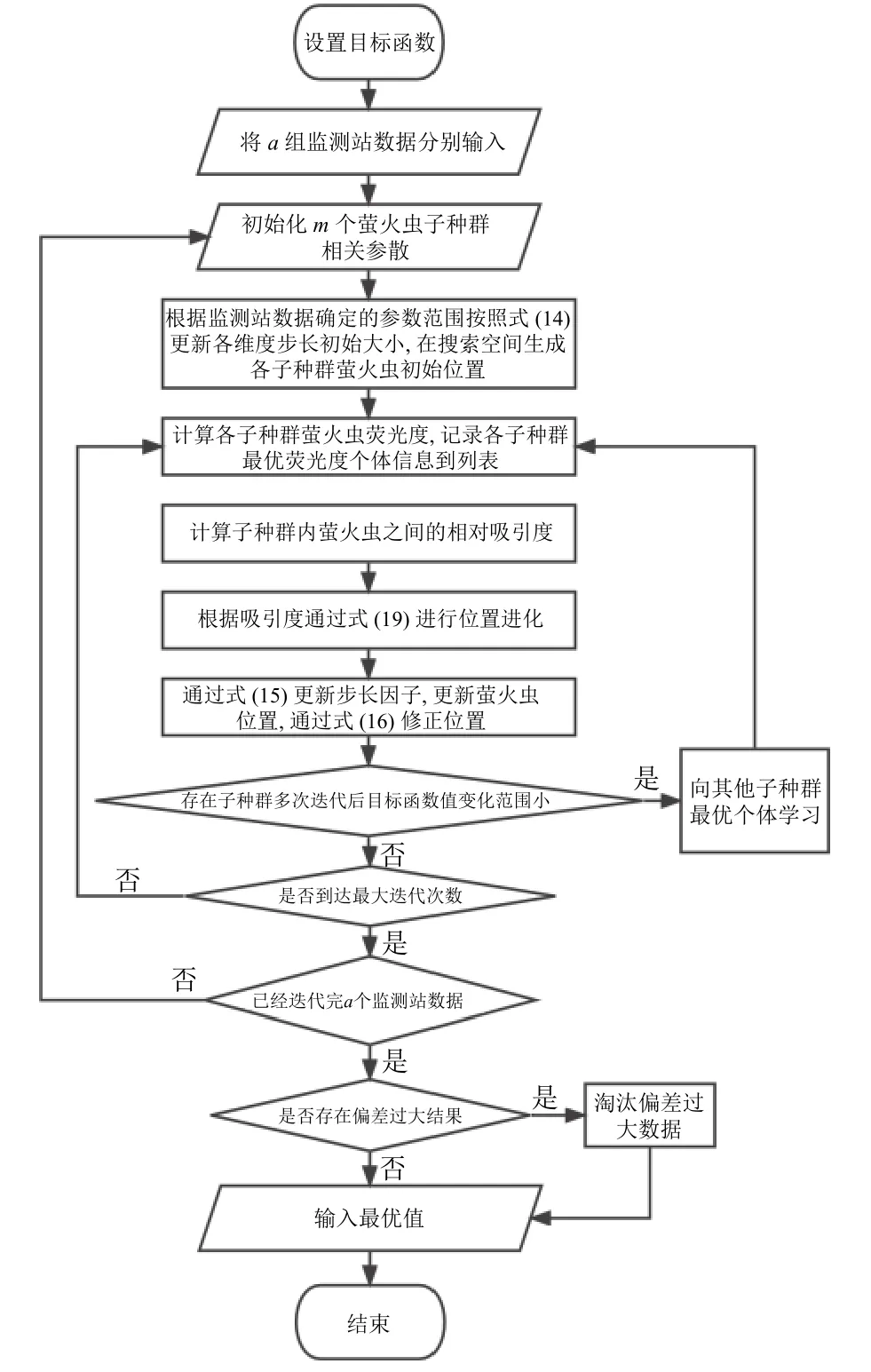
圖1 改進的FA 算法流程圖

步驟1.確定溯源優化模型求解需要求解的內容,式(9)、式(12).

步驟2.設總共有a個監測站的監測數據,每個監測站的污染物濃度系列為mi(i=1,2,…,n),分別將這a個監測站的數據作為初始條件各執行一次步驟3-12的算法內容.

步驟3.假設所有子種群的螢火蟲數目之和為m,子種群數目為n,分別為子種群初始化不同的光強吸收系數 γ、最大吸引度因子 β0,步長因子 α,使各個子種群具有不同的迭代過程.

步驟4.根據監測站數據和河道信息通過式(16)確定需要求解的參數x0,t0,M的上下限.

步驟5.根據參數x0,t0,M的上下限間的大小比例通過式(14)更新各子種群不同維度的步長因子α的初始值.

步驟6.根據步驟4 結果設定不同維度的搜索空間范圍,根據該范圍在不同維度隨機生成螢火蟲的初始位置:

其中,j=1,2···,n;i=1,2,···,m/n,Xij表示在子種群j中第i只螢火蟲的位置,d表示參數的維度.

步驟7.將生成的Xij代入式(9),將式(9)計算結果設置為子種群j中第i只螢火蟲的熒光度I0ij,分別記錄各個子種群中螢火蟲個體熒光度的最大值,將各個子種群和位置Xij記錄在全局信息List列表內.

步驟8.計算子種群內螢火蟲之間的相對吸引度:

其中,rii′表示子種群j中第i和第i′只螢火蟲之間的空間距離,定義為rii′ =||Xij-Xi′j||,Xi′j表示子種群j中第i′只螢火蟲的位置.

各子種群中螢火蟲個體開始位置進化,根據式(19)更新空間位置:

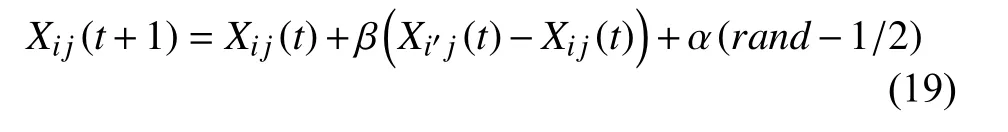
其中,α通過式(15)在每一次迭代前更新大小,rand為在[0,1]內服從均勻分布的隨機因子,t表示當前為第幾次迭代.

根據式(16)修改Xij(t+1)的值,使其不超過步驟4結果中的上下限.

步驟9.查詢List列表數據,若存在某個子種群值在最近10 次迭代變化范圍小于10-3,在List列表中尋找其他子種群中最優秀的螢火蟲個體.

步驟10.如果步驟9 結果存在則向其學習,如果不存在則通過遺傳算法中的變異操作來調整該種群最優螢火蟲個體的位置,從而增加該子種群的種群多樣性,如式(20)、式(21)所示:

其中,η為根據迭代次數t不斷調整的值;N(0,1)為滿足高斯分布均值為0,方差為1 的隨機值.

步驟11.判斷是否達到最大迭代次數,若達到轉步驟12,沒有達到轉步驟7 繼續迭代過程.

步驟12.收集步驟2 中的a個監測站分別迭代后獲取的a組污染物位置x,污染物排放時間t污染物排放濃度M的數據[24].由式(2)可知,在一維模型情況下,給定x時,t也唯一確定,并且M是由確定的x0,t0作為前提條件求得,因此污染物位置x對其他參數有直接影響,求a組數據中污染物位置x的標準差,若標準差過大,代表某個監測站存在不準確濃度數據,將其溯源結果排除,輸出排除后的結果.

4 案例分析

為了驗證提出的改進FA 算法的可行性,本文采用文獻[25]美國地質勘探局公布的2006年在特拉基河做的染料示蹤實驗數據.為了研究混合不均勻情況下監測值對溯源結果的影響[24],采用文獻中低流量(4.05-18.04 m3/s)情景,在監測點1 處投放rhodamine WT 染料0.82 kg、在監測點2-6 處設置監測斷面,監測點1-12 位置如圖2 所示,在監測斷面2 處染料與河流混合不均勻,不同斷面不同時刻的染料濃度系列為文獻[25]中數據,監測點2-6 距染料投放點1 處的位置關系如表1 所示.

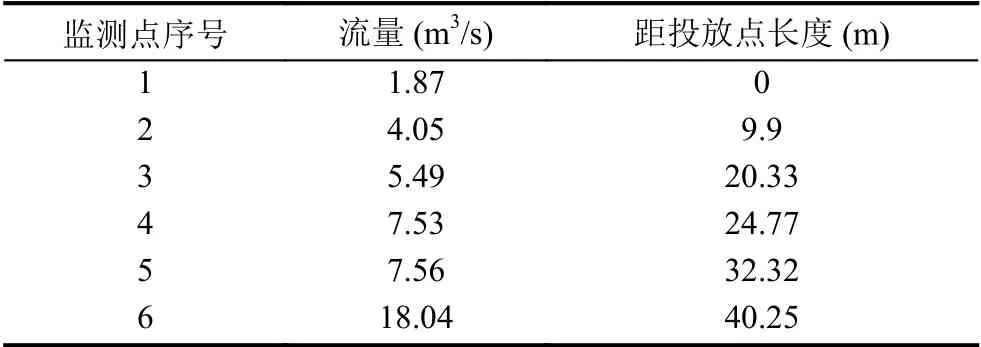
表1 示蹤劑投放監測斷面分布情況

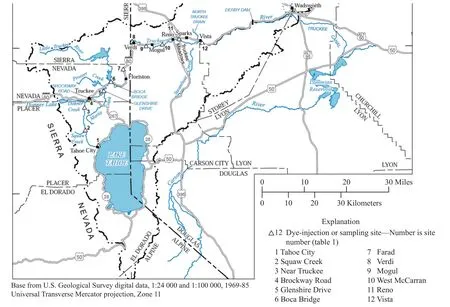
圖2 特拉基河監測站點圖

4.1 溯源參數優化調整

本文使用特拉基河監測斷面的數據,采用改進的FA 的算法對污染物的排放相關的x0,t0,M進行求解.由于算法設置螢火蟲子種群個數n,每個子種群螢火蟲的個數m/n,光強吸收系數 γ、最大吸引度因子 β0,步長因子 α和最大迭代次數Tmax等參數對目標函數,求解時間等有較大影響.因此本文通過多次運行實驗程序,代入不同的螢火蟲算法相關參數,進行對比實驗,最終選取的相關參數如表2 所示.

表2 中FA 算法為單種群算法,只需要輸入一組參數;而本文采用的改進FA 算法在案例分析中子種群數量設置為3,3 個子種群各代入一組參數,由于每組參數中 γ 、 β0,α值不相同,因此各個子種群具有不同的迭代過程,從而避免各子種群同時陷入局部極值的情況,當某個子種群陷入局部極值時可向其他子種群的較優個體學習,跳出局部極值,增加了整個算法的種群多樣性,增強了改進的FA 算法跳出局部極值能力,提高了通過改進FA 算法溯源的準確性.

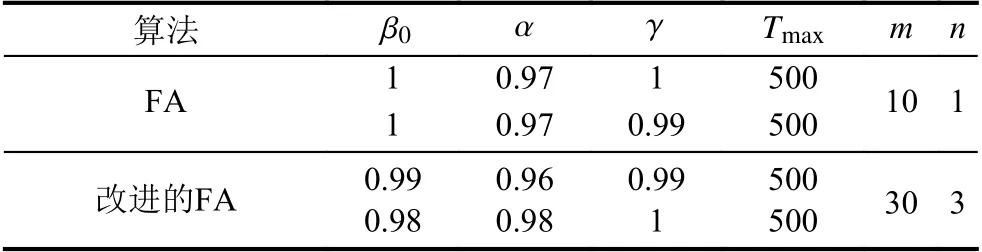
表2 算法參數表

針對河流的水文參數,由文獻[22]可大致估計,污染物的降解系數k為1.7×10-10s-1,監測點2-6 號處河流平均流速u為15 m/s,河流長度方向擴散系數Dx為40 m2/s.Dx為估計值,實際河流中存在Dx、Dy、Dz三種擴散方向,因此需要對參數進行調整.為保證結論正確性,將監測數據分為兩組: 監測斷面2-監測斷面5 號數據設置為實驗集,用來驗證改進FA 算法溯源的準確性; 監測斷面6 號數據設置為訓練集[25],用來調整河流的水文參數.計算方式采用式(9),將Dx設為待求參數,污染源相關參數設為已知,通過改進的FA 算法通過Matlab 軟件進行100 次迭代試算,選取可以使目標函數相對最優的Dx數據為 15.63 m2/s.

4.2 改進FA 算法結果分析

將修正后的水文參數應用到實驗集監測斷面2-監測斷面6 號數據中,分別采用改進的FA 算法和FA 算法對目標函數式(9)、式(12)進行求解,從而對污染源參數排放位置x0、排放時間t0、排放強度M進行求解,改進的FA 算法和FA 算法的迭代過程圖如圖3、圖4所示,其中圖3 為求解目標函數式(9)即求解參數排放位置x0、排放時間t0的迭代過程圖,圖4 為目標函數式(12)即求解參數排放強度M的迭代過程圖.表3 為通過Matlab 軟件運行100 次,去掉偏差過大數據后對剩余數據求平均值得到的數據.

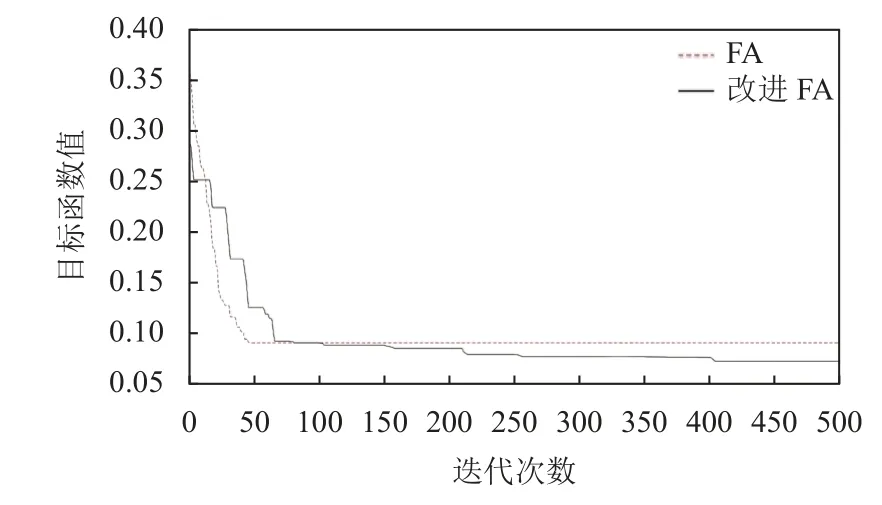
圖3 目標函數1 迭代過程圖

通過圖3、圖4 和表3 可知,FA 算法在迭代到50 代左右時,開始快速收斂,但與真實值相比求解結果偏差較大,問題為陷入局部極值,種群多樣性較低,沒辦法跳出局部極值.改進的FA 算法在300 代左右開始收斂,并且圖像呈現階梯下降趨勢,雖然迭代速度相對于FA 慢,但求解精度高,具有以下優點: 由于引入了自適應步長策略,使算法前期全局搜索能力較強,后期局部搜索精度更高所以具有更好的種群多樣性,全局搜索能力更強; 引入了多種群互相學習策略,當某個種群陷入局部極值時會向其他種群學習或者自身進行高斯擾動,所以具有更好的跳出局部極值能力.

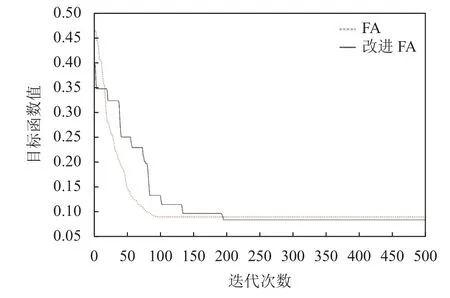
圖4 目標函數2 迭代過程圖

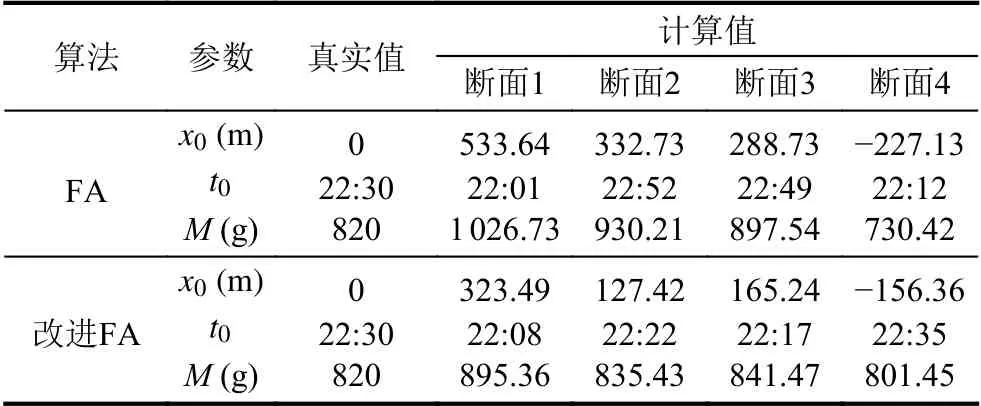
表3 多斷面溯源結果

由表3 可知,斷面2 計算值明顯偏大,根據本文第3.2 節算法步驟,對斷面2-5 溯源得到的污染源位置x0的標準差和去掉斷面2 數據溯源結果對比如表4 所示,排除斷面2 的數據后,標準差明顯降低.

表4 多斷面溯源位置標準差

通過上述溯源結果分析,改進的FA 算法溯源結果污染源位置范圍[-156.36,165.24] m、污染源排放時間范圍[22:17,22:35]、污染源排放強度范圍[801.45,895.36] g 相對于污染源真實值排放位置0 m、排放時間22:30、排放強度820 g 偏差不大.本文方法在實際的河流污染物溯源分析中具有相對的準確性,并且在通過標注差排除異常監測斷面溯源結果后,不同斷面溯源結果相對真實值偏差范圍在可接受范圍內.

5 結論與展望

本研究采用耦合概率密度法和一維水質擴散模型進行建模,通過改進的FA 算法對模型進行求解,為了檢驗算法可靠性采用特拉基河的示蹤劑實驗真實場景數據.在實驗求解過程中通過多次試算的形式對改進FA 算法的最大迭代次數、子種群個數等參數進行合理選取,在確定河流水文參數時,結合資料給定的水文參數(水流速度、降解系數、擴散系數)和通過算法分析對河流長度方向擴散系數進行修正,進一步提高在對河流突發水污染事件溯源的可靠性.最后通過多監測斷面分別進行溯源求解,采用標準差分析法,排除了因為污染物混合不均勻導致的監測數據偏差.通過特拉基河染料示蹤實驗表明,該方法在單污染源識別問題上,其精度高于原始的FA 算法,具有一定的可靠性.