基于三維彎曲激波的寬域變馬赫數乘波體設計分析

尤延鋮，鄭曉剛，丁曉婷，湯祎麒，朱呈祥

（廈門大學航空航天學院，廈門 361005）

人類對于速度的追求是永無止境的。高超聲速飛行器（飛行速度大于5 倍聲速）具備全球實時偵察、快速部署和遠程精確打擊能力，是臨近空間力量部署的重要載體，對國家戰略安全產生重要影響，受到各國的廣泛關注［1-5］。目前，高超聲速飛行器的氣動布局主要包括升力體、軸對稱旋成體、翼身融合體和乘波體等幾種方案［6］。這其中，乘波體布局巧妙利用前緣附體激波防止高壓氣體向上翻洗，被認為是高升阻比飛行器的最佳選擇之一。而美國X-51A 乘波體飛行器的試飛成功更是將乘波原理及其應用研究迅速提升為高超聲速業界密切關注的熱點學術問題［7］。

乘波體又名“導波體”，因其下表面完全“騎乘”在前緣附體激波之上而得名。在設計狀態下，乘波體就像是在水面上打水漂，其形成的前緣附體激波便是乘波體在空中“沖浪”的載體。這一概念最早由Nonweiler 提出，其以斜激波流動為基本流場提出 了“Λ”形 乘 波 體 的 設 計 方 案［8］。Jones 等［9］和Rasmussen 等［10］將基準流場由斜激波流動推廣至軸對稱圓錐流動，提出了錐導乘波理論，有效提高了乘波體的容積率。進一步地，Sobieczky 等［11-12］和Rodi［13］為加強對激波形狀的控制，考慮展向激波曲率的可控設計，發展了吻切錐、吻切軸對稱和吻切流場3 類吻切乘波理論。國內外學者以此為基礎，獲得了構型更為復雜，具有特定目的的一系列新型吻切類乘波構型［14-18］。隨著激波求解技術的發展，一些學者開始嘗試基于全三維非軸對稱激波的乘波設計［19-21］。例如，廈門大學Zheng 等在吻切錐理論的基礎上進一步發展了局部偏轉吻切（Local-turning osculating cones， LTOCs） 方法［22-23］，實現了基于單/多道非軸對稱激波的快速逆向求解［24］，極大拓寬了乘波體的設計空間。

然而，上述方法仍主要集中在特定來流馬赫數條件下進行設計，無法兼顧寬速域、泛空域條件下的氣動特性。為改善乘波體在亞聲速時的氣動性能，Rodi 在吻切理論基礎上推導了激波與乘波體特征曲線之間的幾何關系，首次提出了渦升力乘波體的概念［25-26］。核心是利用特定后掠角度的前緣型線在大迎角下產生上表面分離渦，進而提升乘波體在低速時的升阻特性。國內學者段焰輝等［27］、Liu等［16，28］、Zhao 等［29］對渦升力乘波體的優化設計及其在高/低速時的氣動特性開展了大量研究，加深了對渦升力乘波體的認知。而為改善乘波體在高速范圍內的寬域性能，Wang 等［30］提出將高馬赫乘波體與低馬赫數乘波“前后串聯”組合的設計概念。借鑒該組合設計概念，Li 等［31］提出了“左右并聯”組合的乘波體設計概念，其本質是將多個不同設計馬赫數的乘波體沿展向按照一定的規律進行組合。但是，上述組合乘波體構型在設計選型時更多依賴于設計人員的經驗，在對應設計馬赫數下難以保障優良的“乘波”特性。為此，Zhang 等［32］在“并聯式”組合乘波體的基礎之上，首次提出了錐導變馬赫數乘波體的設計概念。核心是基于錐導乘波理論，改變各吻切平面內的設計馬赫數。Li 等［33］進一步對錐導變馬赫數乘波體設計方法進行拓展，提出了等錐角變馬赫數乘波體設計方法。隨后，Zhao 等［34］將變馬赫數乘波概念與吻切錐理論相結合，提出了吻切錐變馬赫數乘波體設計方法，并探討了不同馬赫數離散方式對此類乘波體性能的影響［35］。類似地，Liu 等［36］進一步利用吻切流場理論對變馬赫數乘波概念進行了相關的研究。上述變馬赫數乘波設計方法的研究，在不同程度上提高了乘波體飛行器在非設計條件下的氣動性能，使其能更好地適應從起飛爬升到高空高速巡航的寬域飛行環境［37］。

不難發現，現階段有關變馬赫數乘波體的設計方法都是基于錐導或吻切乘波理論開展的，其對應激波面仍局限于圓錐激波或圓錐激波的掃掠面，形狀相對單一，難以同日益復雜的進氣道唇口相匹配，極大地限制了此類乘波體的設計自由度。針對這一問題，本文將變馬赫數乘波概念與LTOCs 方法相結合，提出了一種基于三維彎曲激波的寬域變馬赫數乘波體設計方法。該方法采用Bezier 曲面形式來指定預設計激波以加強對三維激波面的控制。在接下去的研究內容中，將首先詳細介紹基于三維彎曲激波的寬域變馬赫數乘波體設計方法；隨后，通過數值仿真研究驗證該方法的有效性，并探討不同馬赫數離散單調性對此類乘波體構型和氣動性能的影響；最后，在相同約束條件下，將基于三維彎曲激波設計的變馬赫數乘波體與常規吻切錐變馬赫數乘波體進行對比，以證明本文所提出設計方法的優越性。

1 寬域變馬赫數乘波體設計方法

1.1 局部偏轉吻切方法概述

為了更好地介紹本文所提出的基于三維彎曲激波面的變馬赫數乘波體設計方法，下面將首先對LTOCs 方法的原理進行簡單的回顧。受吻切錐導理論離散流場的啟發，LTOCs 方法首先將三維曲面激波在橫向上進行離散，隨后結合當地激波曲率沿流向進一步離散，在各微元吻切平面內進行二維求解以此實現三維流動的簡化。由于以當地激波曲率的方式引入了橫向流動所帶來的影響，各微元吻切平面會隨著流向不斷發生偏轉，這一方法也因此特點而得名。可見，LTOCs 方法同樣采用了降維求解思路，將復雜的三維流動降階為一系列切片內的二維流動進行求解。不同之處在于，LTOCs方法中的切片不再是單一的平面，而是由一系列微元吻切平面組成的曲面，其完整包含了當地流線，本質上是一張流面。有關LTOCs 方法求解復雜三維彎曲激波的步驟在文獻［23］中已詳細介紹，在此不再贅述。

通過上述離散降維方式，LTOCs 方法能夠實現基于復雜三維彎曲激波面的逆向乘波設計。圖1給出了基于LTOCs 方法設計外流乘波體的原理圖，圖中FCT 代表設計平面的流量捕獲曲線（Flow capture tube）。進一步地，在利用LTOCs 方法進行逆向設計時，乘波體上下表面上各點處的壓力均是可求的，這便為計算乘波體的升阻力特性提供了可能。如圖2 所示，乘波體下表面各網格點的壓力值均可通過LTOCs 法方法求得，通過積分下表面上每個四邊形微元所受到的壓力便可求得該表面的受力情況。上表面通常被指定為平行來流的自由流面，其上壓力實際上便是自由來流的壓力。由此，在不考慮底阻的情況下，整個乘波體所受到的升力和阻力便是上下表面的受力之和，具體求解過程詳見文獻［23］。

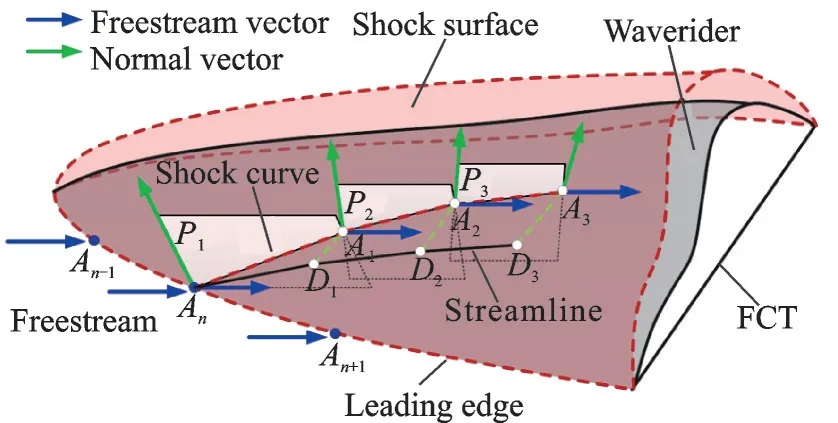
圖1 基于LTOCs 方法的乘波體設計示意圖[23]Fig.1 Schematic of waverider design based on the LTOCs method[23]

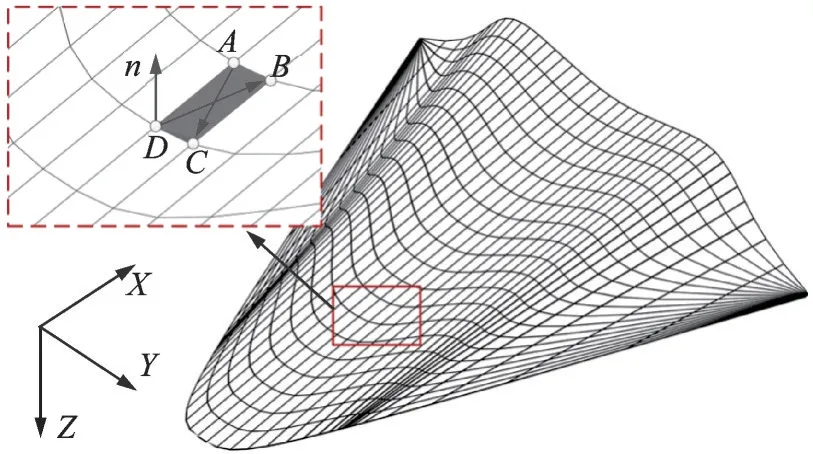
圖2 乘波體下表面升阻力求解示意圖[23]Fig.2 Schematic of lifting resistance solution on lower surface of waverider[23]

1.2 基于三維彎曲激波的變馬赫數乘波體設計步驟

如前所述，本文提出的基于三維彎曲激波的變馬赫數乘波體設計方法的核心是將變馬赫數乘波概念與LTOCs 方法相結合，在前緣離散點對應的流面內按需指定不同的設計馬赫數。圖3 給出了基于三維彎曲激波的變馬赫數乘波體設計原理圖，圖中SWPC 為設計平面內的激波輪廓線（Shock wave profile curve），其本質是三維激波面與設計平面的交線。基于三維彎曲激波的變馬赫數乘波體設計大致可分為3 步。

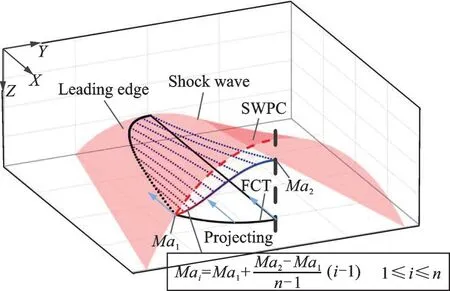
圖3 基于三維彎曲激波的變馬赫數乘波體設計原理圖Fig.3 Design schematic diagram of variable Mach number waverider based on 3D curved shock wave

（1）指定變馬赫數乘波體所“騎乘”的三維彎曲激波面。不同于現有吻切錐變馬赫數乘波體，本文對于激波的設計不再僅限于設計平面內SWPC 曲線的調節，而是對全流場所具有的三維激波形狀進行設計（即圖3 中紅色曲面Shock wave），理論上任意滿足設計的三維曲面方程均可作為預設計三維彎曲激波面。為加強對激波形狀的控制，本文采用Bezier 曲面形式來指定三維彎曲激波面，相關概念及設計參數在下文給出。

（2）設計生成乘波體前緣型線的三維構型及相應上表面。為保證乘波體邊緣不產生溢流以提供較高的升阻比，在前緣型線的設計中需保證前緣型線與三維激波曲面相交。因此，本文采用在設計平面內指定FCT 曲線、水平向前投影至三維彎曲激波面的形式來生成所需乘波體前緣型線。由于FCT 曲線對乘波體性能的影響并不是本文的研究重點，指定變馬赫數乘波體的FCT 曲線方程為二次曲線

式中A和R為無量綱常數。變馬赫數乘波體的上表面則是將FCT 曲線水平向前投影所形成的自由流面。

（3）引入變馬赫數概念，利用LTOCs 方法求得各流面內的流線以組合形成變馬赫數乘波體下表面。將前述得到的前緣型線離散成n個點，基于LTOCs 方法沿流面追蹤這些離散點發出的流線，并對其進行三維組合形成變馬赫數乘波體的下表面。本文的創新之處在于，利用LTOCs 方法進行流線追蹤時，各流面內的設計馬赫數不再固定，可適當調整以滿足寬域飛行需求。文獻［29］詳細對比了線性函數、正弦函數和余弦函數等不同設計馬赫數離散方式對吻切錐變馬赫數乘波體構型與氣動性能的影響，并指出設計馬赫的離散單調性影響最大。參照該文獻，本文選取線性函數來定義各流面內的馬赫數離散方式。

具體而言，如圖3 所示，根據所給定的設計馬赫數區間［Ma1，Ma2］，以等差數列的分布規律為每一前緣離散點所對應的流面配置相應的設計馬赫數，圖中彩色虛線代表不同流面內的乘波體下表面流線，不同顏色對應不同的設計馬赫數。具體為：定義變馬赫數乘波體最外緣流面內的設計馬赫數為Ma1，對稱面內的設計馬赫數為Ma2，則前緣型線第i個離散點對應流面內的設計馬赫數為

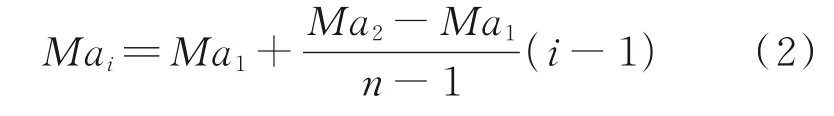
需要特別說明的是，變馬赫數乘波體最外緣處的坐標由三維彎曲激波面與FCT 曲線唯一確定，此流面內設計馬赫數的變化并不會對其坐標產生影響。

1.3 基于Bezier 曲面的三維彎曲激波面定義

激波作為高超聲速流動中最為顯著的物理特征，其在很大程度上影響著乘波飛行器的氣動性能。得益于LTOCs 方法求解三維激波的便捷性，本文提出的寬域變馬赫數乘波體設計方法能夠實現針對復雜三維彎曲激波的變馬赫數乘波設計。為加強對激波的控制，本文采用Bezier 曲面來定義預設計激波。在介紹Bezier 曲面之前，首先對Bezier 曲線的基本原理進行簡單介紹。常規的曲線表示方式存在諸多不足，例如無法精確表示所有曲線、不易求法向量和對舍入誤差較為敏感等。Bezier 曲線的概念由此而生，幾何學中Bezier 曲線是多個控制點決定的光滑矢量曲線，由可移動節點與可伸縮線段共同組成，其具體表達式為

而Bezier 曲面本質上是通過張量積分法將一元Bernstein 多項式基推廣至二元Bernstein 多項式基，以此實現Bezier 曲線向Bezier 曲面的推廣。換言之，Berzier 曲面可看作是兩條不同方向上Bezier曲線的張量積。考慮到矩陣計算的簡潔性，Bezier曲面對應的參數化方程可以用如下矩陣形式進行表達

式中：h、t分別表 示m、n兩個方 向上Bezier 曲線的控制點數目，Pij為控制點坐標矩陣，M1和N1分別為向量M和N對應的系數矩陣。在實際應用中，兩個方向上Bezier 曲線的控制點數目h、t值均應不大于4。因此在后續內容中，考慮可操縱性，本文選用3×4 個點控制的Bezier 曲面作為變馬赫數乘波體所“騎乘”的預設計三維激波面，其表達式為

圖4 進一步給出了上述3×4 個點控制的Bezier 曲面示意圖，藍色空心節點代表控制節點，用線段逐次連接相鄰控制點所形成的空間網格被稱作控制網格，即圖中藍色虛線網。控制網格中邊緣控制點用于定義Bezier 曲面邊緣曲線的形狀，而控制網格內部點則主要用于控制該曲面內部的形狀。如 圖4 所 示，P20至P23四 點 控 制 的Bezier 曲 線實際上便是設計截面內的激波曲線SWPC。利用方程（5）只需指定曲面控制點的坐標矩陣Pij，便可實現對三維激波面的調控。需要注意的是，激波曲面的曲率方向決定著氣流的壓縮方式（向內壓縮或向外壓縮），不同壓縮方式的求解過程顯然是不同的。考慮到求解的復雜性，在指定控制點坐標時應避免出現激波曲率方向變化的情況且應確保該激波面在物理上是正確的。

圖4 3×4 階Bezier 曲面及其控制網格示意圖Fig.4 Schematic of 3×4-order Bezier surface and its control grid

2 寬域變馬赫數方案與計算條件

2.1 寬域變馬赫數乘波體方案

為驗證上述基于三維彎曲激波的變馬赫數乘波體設計方法的有效性，同時研究設計馬赫數的離散單調性對此類乘波體性能的影響，本文共設計了4 個不同馬赫數分布的變馬赫數乘波體構型，分別命名為Case 1 至Case 4。基于控制變量的思想，乘波體對應的預設計激波形狀以及FCT 曲線均完全相同。同時，為兼顧容積特性與氣動特性，取FCT曲線方程為

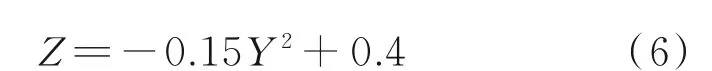
表1 給出了4 個乘波體對應的設計馬赫數離散分布特征，表中Ma1和Ma2分別對應乘波體最外緣流面與對稱面內設計馬赫數（見圖3）。Case 1 和Case 4 分別為設計馬赫數為7 和12 的定馬赫數乘波體，而Case 2 和Case 3 則對應不同馬赫數離散單調性的變馬赫數乘波體。

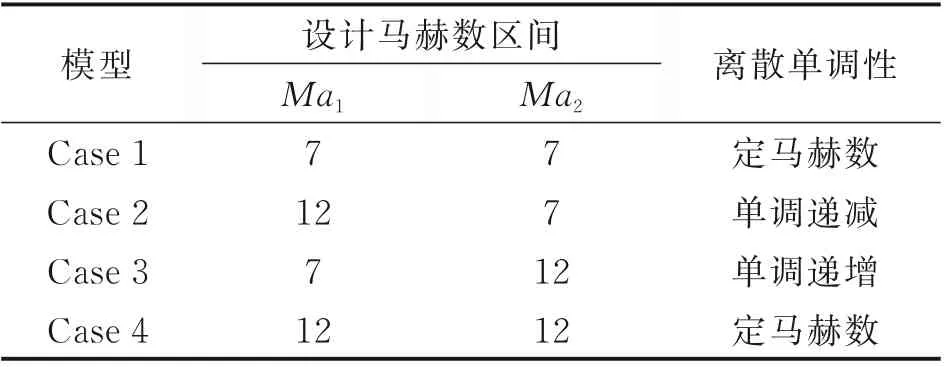
表1 乘波體設計馬赫數分布特性對比Table 1 Comparion of Mach number distribution characteristics for waverider design

由于4 個乘波體對應的預設計激波形狀與FCT 曲線相同，其三維前緣型線完全一致，四者在構型上的差異主要體現在橫向截面內。圖5 給出了上述4 個乘波體尾緣形狀（Trailing edge，TE）的對比圖。如前所述，LTOCs 方法中各流面內的基本流場實際上是多個局部圓錐流動的耦合。參照圓錐流動特性可合理預測，在相同激波下，基于LTOCs 方法求得的壓縮型線尾緣點至SWPC 線的距離會隨著馬赫數增加而逐漸減小。換言之，設計馬赫數越高，對應的乘波體越厚。因此，如圖5所示，4 個乘波體中Case 4 的尾緣線最厚，Case 1 最薄，而兩變馬赫數乘波體Case 2 與Case 3 的尾緣線介于兩定馬赫數之間。在對稱面上，Case 1 與Case 2 的尾緣線重合，Case 3 與Case 4 的尾緣線重合，這主要是因為它們在對稱面內的設計馬赫數相同。除此之外，從圖中可以看到兩變馬赫數乘波體Case 2 和Case 4 的尾緣線在靠近邊緣的D點相交，Case 3 的尾緣形狀在大部分區域內均要厚于Case 2。這表明在D點所對應的流面內，兩者的設計馬赫數相同，且Case 3 的容積整體要大于Case 2。

圖5 基于三維彎曲激波設計的變馬赫數乘波體后緣形狀對比Fig.5 Comparison of trailing edges for four variable Ma number waveriders based on 3D shock waves

圖6 進一步給出了上述乘波體詳細的幾何參數對比，圖中Lw、W和H分別表示乘波體的長度、寬度以及高度，Sw為迎風面積，Sp為乘波體在水平面上的投影面積，Sb為設計截面投影面積，而V則表示乘波體的容積。如前所述，4 個乘波體具有完全相同的三維前緣型線，其在長度、寬度以及水平投影面積方面是一致的。Case 1 與Case 2 的迎風面積差異不大，Case 3 與Case 4 也幾乎相同，而高馬赫數設計的Case 4 的迎風面積則相較于低馬赫數設計的Case 1 提升約1.25%。四者幾何參數的差異主要體現在垂直投影面積與容積上。在垂直投影面積方面，Case 4 面積最大，Case 1 最小，而變馬赫數乘波體Case 2 和Case 3 介于兩者之間，且Case 3 的垂直投影面積要大于Case 2。相較于Case 1，Case 2、Case 3 和Case 4 的垂直投影面積分別增加約13.42%、22.79%和27.92%。4 個乘波體在容積方面也表現出了相同的規律。Case 2、Case 3 和Case 4 的容積相較于Case 1 分別增長了約12.22%、23.79% 和28.75%。此外，在容積率方面，相較于Case 1，Case 2、Case 3 和Case 4 的容積率分別增長約8.25%、15.53%和18.45%。

圖6 基于三維彎曲激波設計的變馬赫數乘波體幾何參數對比Fig.6 Comparison of geometric parameters for four variable Ma number waveriders based on 3D shock waves

2.2 數值方法概述及網格無關性驗證

參照文獻［27］，本文采用商用軟件Fluent 對上述4 個基于三維彎曲激波面的定/變馬赫數乘波體在設計馬赫數區間內的7、8、9、10、11、12 等6 個馬赫數，高度27 km，不考慮迎角與側滑角的條件下開展無黏數值模擬。選用密度基求解器，對流通量采取二階AUSM 迎風差分格式，來流假定為理想氣體。計算時監測殘差變化、計算域進出口質量流量差以及乘波體表面的平均靜壓。當殘差曲線至少下降3 個數量級、進出口流量差值與進口流量之比小于0.01 且乘波體表面的平均靜壓保持不變時即判定計算收斂。上述數值方法設置在文獻［22-24］中已得到驗證，便不再贅述。

本文以Case 2 為例進行了網格無關性驗證。為保證激波的精確模擬，采用分區結構化網格，同時考慮模型的對稱性，僅對半模進行劃分。在乘波體表面布置有C 形網格，并對壁面附近及乘波體前緣進行了加密處理。本文共劃分了3 種疏密程度的結構網格，即粗網格（網格量3 780 740 個）、中網格（網格量5 880 630 個）和細網格（網格量7 621 030個），并利用上述數值方法對3 種網格在馬赫8，高度27 km 的條件下進行無黏數值模擬。圖7 給出了中等尺度網格結構的示意圖，其他尺度網格與之類似。3 種尺度網格在X/Lw=0.75 截面內的上下壁面壓力對比結果如圖8 所示。可以看到，3 種尺度網格求得的上下壁面壓力具有良好的吻合度，特別是中等尺度與細尺度網格，其最大誤差僅為0.213%左右。這種誤差在實際的數值模擬過程中是完全可以接受的。因此，在后續的數值計算中均采用中等尺度網格進行數值計算以節約計算資源。

圖7 Case 2 中等尺度結構網格示意圖Fig.7 Schematic of the medium structured grid for Case 2

圖8 Case 2 中X/Lw=0.75 截面上下壁面壓力對比Fig.8 Pressure distribution on X/Lw=0.75 plane of Case 2 in grid independence analysis

3 變馬赫數乘波體性能驗證分析

3.1 波系結構驗證分析

為驗證基于三維彎曲激波的變馬赫數乘波體概念的可靠性，本節將首先對上述4 個乘波體的波系結構進行分析。圖9 給出了定馬赫數乘波體（Case 1 和Case 4）在各自設計點時的波系結構對比圖。圖中淡紅色透明曲面表示預設計的三維彎曲激波面，紅色實線為不同橫截面內的預設計激波曲線。從圖中可以看到，在各自設計馬赫數下，兩個乘波體均表現出極佳的乘波特性。各橫截面內，乘波體前緣線處均未出現明顯的高壓溢流，且無黏CFD 計算求得的激波形狀與預設計激波形狀基本重合。由此可見，基于LTOCs 方法設計的定馬赫數乘波體在設計條件下能夠較為精確地復現預先指定的全三維彎曲激波，這一方法在設計定馬赫數乘波體的精度是令人滿意的。

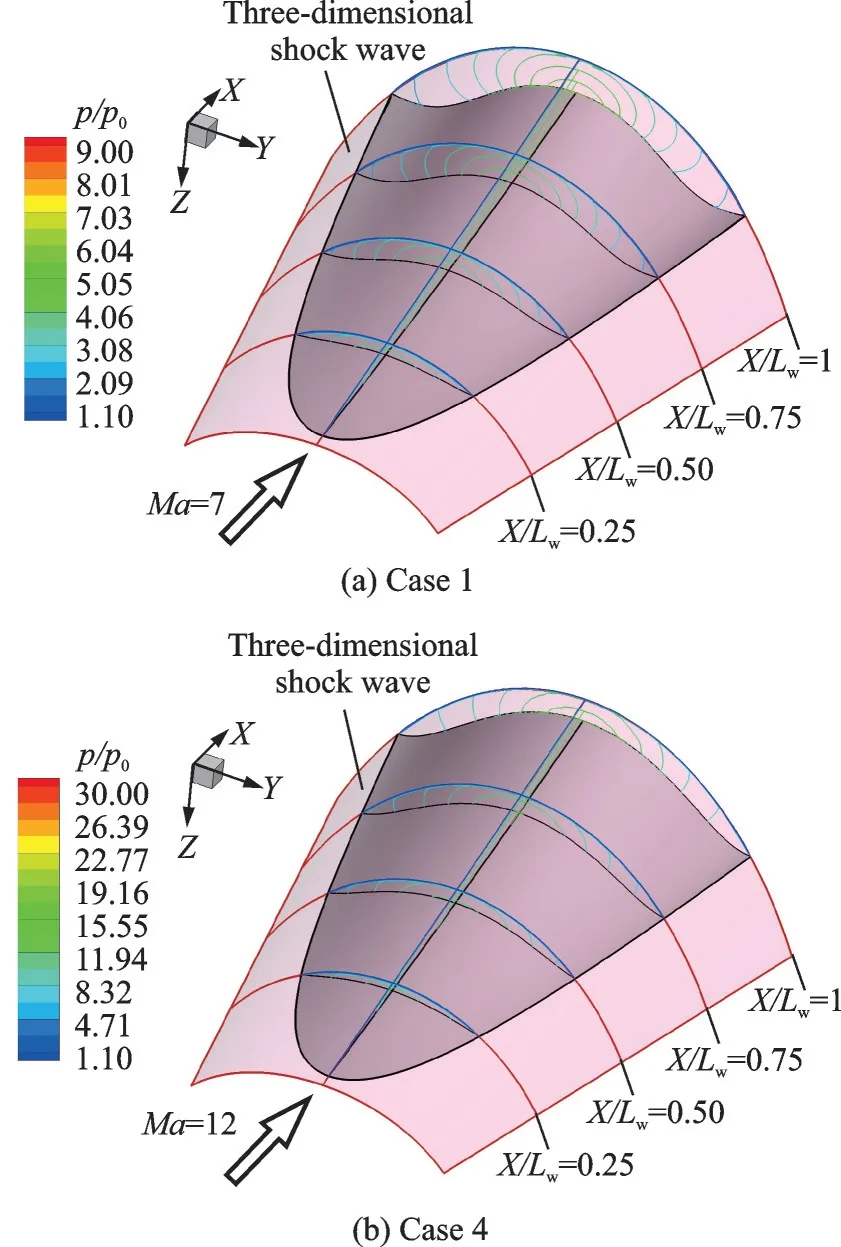
圖9 定馬赫數乘波體設計馬赫數下三維激波形狀對比Fig.9 Comparison of 3D shock waves for constant Mach number waveriders under design conditions

圖10 則給出了不同馬赫數下，兩變馬赫數乘波體在設計截面內的波系結構對比圖，圖中紅色虛線代表設計平面內的預設計激波形狀。可以看到，對于變馬赫數乘波體而言，各馬赫數下無黏CFD計算求得的激波形狀同設計激波之間的差異較大。這主要是因為變馬赫數乘波體的下表面實際上是由一系列不同設計馬赫數的流線“并聯”組合而成，特定條件下必然存在部分流線位于非設計狀態。馬赫7 時，無黏計算求得的Case 2 的激波與預設計激波在對稱面處基本重合，而Case 3 對稱面處的激波則要明顯高于預設計激波。在乘波體邊緣，兩乘波體均出現了脫體激波，且Case 2 的溢流現象要明顯大于Case 3。隨著馬赫數的增加，二者的激波脫體現象均有所改善。馬赫9 時，Case 3 邊緣處的脫體激波已基本消失，而Case 2 邊緣處仍存在部分溢流，但溢流程度相較于馬赫7 時下降明顯。馬赫12 時，Case 3 對稱面處的激波形狀與預設計激波形狀基本重合，而Case 2 對稱面處的激波則要明顯低于預設計激波。對比邊緣處的激波形狀可以看到，此時Case 2 的激波形狀與預設計激波大致重合，而Case 3 邊緣處的激波則與下表面較為貼近，且存在一定的激波系間的相互干擾現象。綜合來看，即便變馬赫數乘波體在三維激波形狀的復現上存在一定的差異，其整體的乘波特性仍是令人滿意的，尤其是高馬赫數下。這也表明本文提出的基于三維彎曲激波的變馬赫數乘波體概念是可行的。

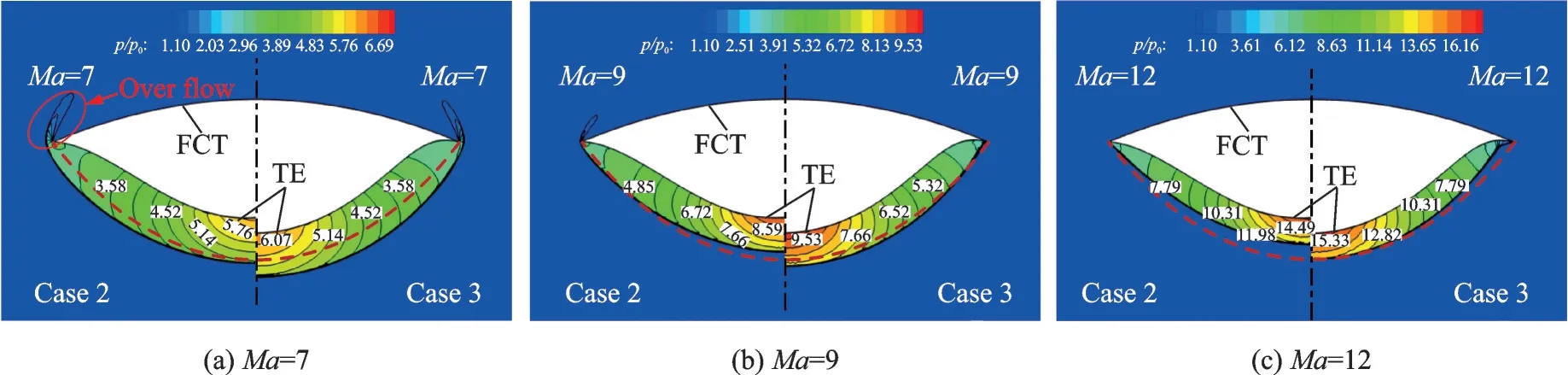
圖10 變馬赫數乘波體變馬赫數下設計截面波系結構對比Fig.10 Comparison of shock structures on the base plane for variable Mach number waveriders under different conditions

3.2 壁面壓力驗證分析

對于乘波體而言，其表面的壓力分布是衡量乘波體性能的又一重要參數。因此，本文將參照文獻［30］，對上述乘波體在不同橫截面內的上下壁面壓力進行對比分析。圖11 給出了馬赫9 時，前述乘波體在4 個不同橫截面內（橫截面相對位置如圖9 所示）的壁面壓力對比結果。各圖片上半部分為上壁面壓力分布，而下部分則為下壁面壓力分布，且均只給出了Y軸負半軸上的結果。當乘波體的上下壁面之間未出現溢流時，上壁面的壓比應為1。而出現脫體激波時，上壁面的壓力則會出現一定的壓力波動。因此，上壁面的壓力分布可用于判斷此時是否有脫體激波的產生。由圖可知，低馬赫數設計的定馬赫數乘波體Case 1 在各橫截面內，上壁面壓力均未出現明顯的壓力波動，并未產生脫體激波。這主要是因為Case 1 的設計馬赫數為7，在馬赫9時其產生的激波會變得更為貼體。變馬赫數乘波體Case 3 的上壁面同樣也未觀察到明顯的壓力波動，而變馬赫數乘波體Case 2 則在X/Lw=0.75 和X/Lw=1 兩截面內出現了壓力波動，這一結果與圖10（b）是一致的。高馬赫數設計的定馬赫數乘波體Case 4 上下壁面間的溢流現象最為明顯，在3 個橫截面內均出現了壓力波動。總的來看，上述乘波體上壁面的壓力脈動僅占上壁面的極小部分，這表明基于三維彎曲激波面的變馬赫數乘波體在非設計狀態下仍具有良好的乘波特性。

圖11 Ma=9 時4 種乘波體不同橫截面內上下壁面壓力對比Fig.11 Comparison of static pressure distributions at different cross sections under Ma=9 condition for four waveriders

對于下壁面而言，4個乘波體的壁面壓力均表現出了由外向內逐漸遞增的趨勢。各橫截面內，變馬赫數乘波體Case 2的壁面壓力在邊緣處與Case 4的壁面壓力基本相同，而在對稱面處則同Case 1 的壁面壓力基本重合。與之相反，Case 3 在對稱面處與Case 4 的壓力基本重合，在邊緣處與Case 1 的壁面壓力基本相同。這一壓力分布特性再次證明了本文所提出設計方法的正確性。4 個乘波體下壁面的平均壁面壓力大致關系為：Case 4＞Case 3＞Case 2＞Case 1，這說明4 個乘波體中，Case 4 對應壓縮效率最高，Case 1 最低，而Case 2 和Case 3 的壓縮效率介于兩者之間。可見，設計馬赫數的離散分布規律對此類乘波體的壓縮效率有著顯著的影響，可通過調節馬赫數離散分布特性實現所需的壓縮特性。

3.3 氣動性能驗證分析

如前所述，利用LTOCs 方法設計定馬赫數乘波體時可快速預估其升阻特性。表2 給出了定馬赫數乘波體（Case 1 和Case 4）在各自設計點時的無黏氣動力參數對比結果。其中，氣動力參數的相對變化量均是相對于無黏CFD 結果。由表中數據可知，LTOCs 方法求得的氣動力參數與CFD 結果基本一致，兩乘波體對應的氣動力誤差均小于0.6%。這一結果再次證明了LTOCs 方法在特定馬赫數下進行外流乘波體設計的高精確性。

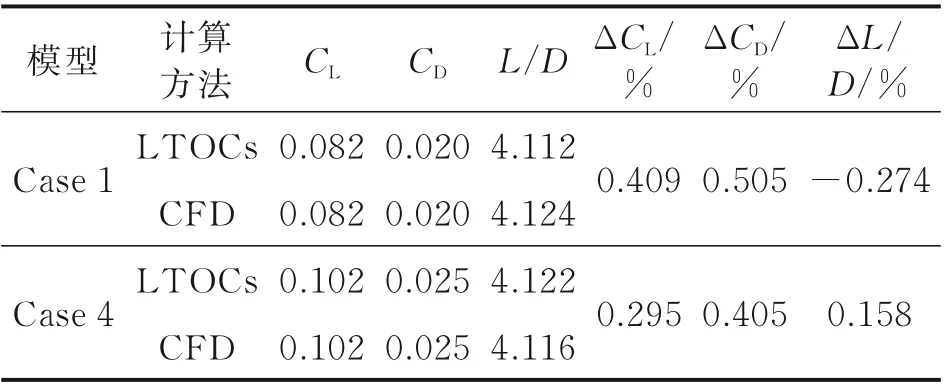
表2 定馬赫數乘波體設計馬赫數下氣動力參數對比驗證Table 2 Comparison of aerodynamic parameters for constant Mach number waveriders

為進一步分析變馬赫數概念對乘波體升阻特性的影響，圖12 給出了4 個乘波體在不同馬赫數下的升阻特性對比結果，其中Xcp表示乘波體壓心的相對位置。從圖12（a）中可以看到，4 個乘波體的升阻比均隨著馬赫數的增加而增大。其中，低馬赫數設計的定馬赫數乘波體Case 1 升阻比最大，高馬赫數設計的定馬赫數乘波體Case 4 升阻比最小，而變馬赫數乘波體Case 2 和Case 3 的升阻比則介于兩者之間。在不同馬赫數下，Case 3 與Case 4 的升阻比較為接近，隨著速度的增加，兩者之間的差距進一步縮小。結合4 個乘波體間的幾何關系（見圖6），不難發現基于三維彎曲激波的變馬赫數乘波體的升阻比與容積之間同樣存在矛盾關系，在設計過程中需要綜合考慮這些參數之間的折中處理。如圖12（b）所示，4 個乘波體的壓心相對位置隨著馬赫數的增加而后移，但后移幅度相對較小，滿足操穩特性的需求。4 個乘波體中，Case 3 的壓心最靠前，Case 2 的壓心最靠后，而定馬赫數乘波體Case 1 和Case 4 的壓心位置介于兩者之間。總體而言，基于三維彎曲激波面的變馬赫數乘波體相對于定馬赫數乘波體而言擁有更為均衡的氣動性能與幾何特性，更適于寬速域飛行，這一結果與現有錐導/吻切變馬赫數乘波體基本一致。變馬赫數概念的引入使得乘波體性能邊界擴大，進一步拓寬了乘波體的設計自由度。

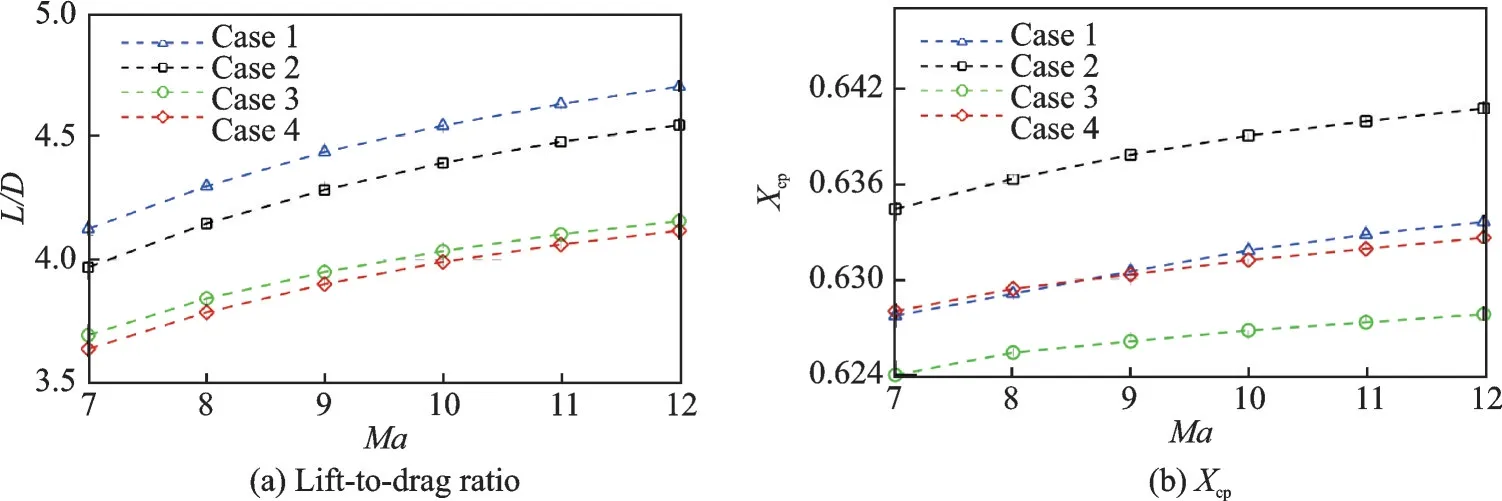
圖12 不同馬赫數氣動力參數對比Fig.12 Comparison of aerdynamic perfomances at different Mach numbers

4 與吻切變馬赫數乘波體對比分析

為進一步揭示基于三維彎曲激波的變馬赫數乘波體設計方法的優勢，本節利用現有吻切錐變馬赫數乘波體設計方法設計了變馬赫數乘波體Case 5。設計時，令Case 5 對應設計截面內FCT曲線、SWPC 曲線以及馬赫數離散分布方式與Case 2 完全相同。設計激波角度的選取則是為了保證Case 2 與Case 5 的長度基本一致。兩乘波的幾何構型及相應幾何參數對比如圖13 所示，圖中的各參數相對關系是相對于Case 5 而言的。從圖中可以看到，兩個乘波體的長度與寬度基本相同，差異主要體現在前緣型線及各橫截面內的輪廓線上。Case 2 的前緣型線相較于Case 5 更寬，而設計平面內Case 5 的輪廓線整體要厚于Case 2。盡管兩乘波體設計截面內的SWPC 曲線是一致的，但對應的三維激波形狀是完全不同的。Case 2 對應三維激波形狀為Bezier 曲面（見圖4），而Case 5 的三維激波形狀則是圓錐激波母線沿SWPC 曲線的掃掠曲面。以對稱面為例，Case 5 在對稱面內的激波為一條直線，而Case 2 則為一條曲線，這也就導致了兩者在對稱面內構型的差異。如圖13（b）所示，兩個乘波體的高度與容積差異較小，Case 2 相較于Case 5 分別增長了約0.87%與1.03%。在關鍵面積參數方面，兩者的差別則較為明顯，Case 2的迎風面積與水平投影面積分別增長約12.43%與14.47%，而垂直投影面積則減小約5.06%。由于Case 2 的容積增長幅度要遠小于水平投影面的增長幅度，Case 2 的容積率要小于Case 5，相對減小約11.86%。

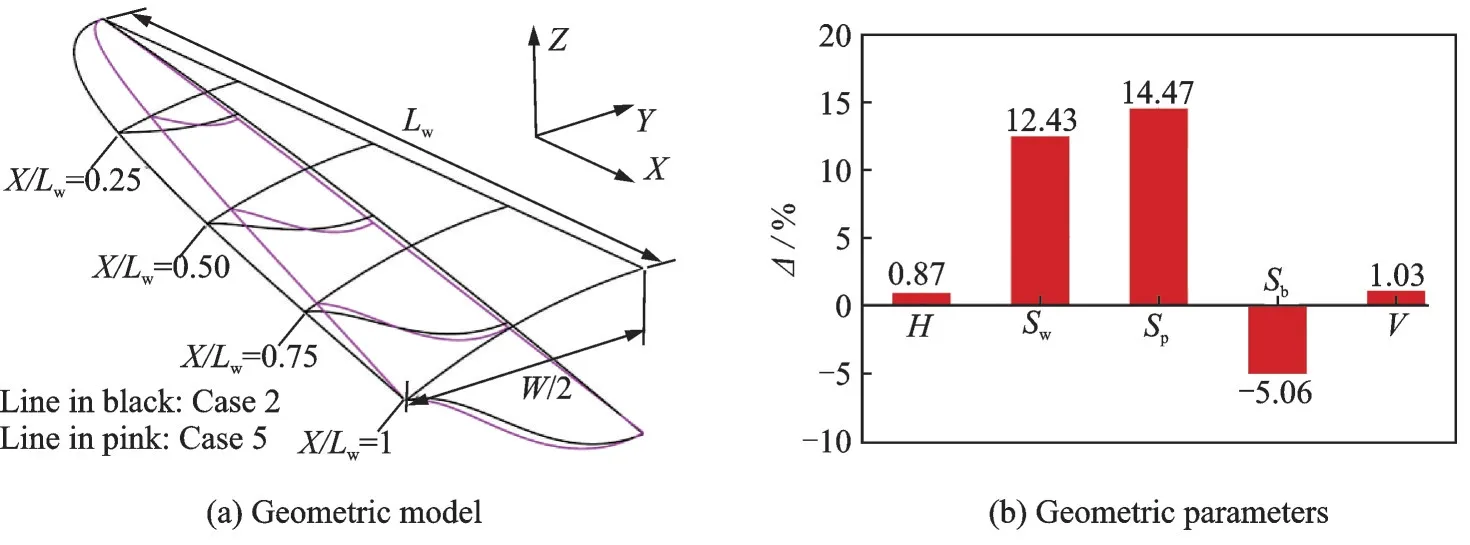
圖13 Case 2 與Case 5 幾何構型對比Fig.13 Comparison of geometric characteristics for Case 2 and Case 5

兩乘波體在非設計狀態馬赫9 時的波系結構與壁面壓力分布對比結果如圖14 所示。如圖14（a）所示，兩乘波體在對稱面處的激波形狀基本差別不大，且略低于預設計激波，這主要是因為兩乘波體在對稱面處的高度大致相同。在乘波體的外緣處，兩乘波體均出現了高壓溢流，且Case 5 的溢流程度要明顯強于Case 2，這表明Case 2 的乘波特性要優于Case 5。圖14（b）則給出了該馬赫數下，兩乘波體在設計截面內上下壁面的壓力分布對比結果。可以看到，兩乘波體在上表面均出現了壓力波動，并且Case 5 上壁面壓力波動所占的比例要明顯大于Case 2。這也說明馬赫9 時Case 2 展示出了更佳的乘波特性，這與圖14（a）是一致的。對于乘波體下壁面壓力而言，Case 2 表面的壓力沿外緣向對稱面逐漸增加，而Case 5 的壁面壓力則呈現遞減的趨勢，但下降幅度較小。比較而言，Case 5 下壁面的平均壓力要大于Case 2，這是由Case 5 下壁面總體厚度更大，相應激波強度更強導致的。圖15 進一步給出了兩乘波體在不同馬赫數下的升阻比對比結果，圖中升阻比相對大小關系是相較于Case 5 的。如 圖15 所 示，各 馬 赫 數 下，Case 2 的 升阻比均要大于Case 5，且兩者間的差距隨著馬赫數的增加而略有增加，但增長幅度略有減緩。馬赫12 時，兩者升阻比差距最大，Case 2 的升阻比提升約13.36%。

圖14 馬赫9 時Case 2 與Case 5 流場分布對比Fig.14 Comparison of flowfields under Ma=9 condition for Case 2 and Case 5

圖15 各馬赫數下Case 2 與Case 5 升阻比對比Fig.15 Comparison of lift-to-drag ratio under differnt conditions for Case 2 and Case 5

綜上，基于吻切錐理論設計的變馬赫數乘波體不可避免地存在著與常規定馬赫數吻切錐導乘波體一樣的問題，其對應的三維激波面僅由設計激波角度與設計截面內SWPC 曲線決定，這也導致了吻切錐變馬赫數乘波體在設計中受到了較大的約束。相比之下，本文提出的設計方法可借助Bezier曲面直接指定激波面的全三維形狀，變馬赫數乘波體的設計空間進一步擴大。上述對比結果說明，在相同SWPC 曲線及幾何約束下，通過合理指定激波的三維形狀可使得此類變馬赫數乘波體較現有吻切錐變馬赫數乘波體擁有更大的升阻比，進一步證明了本文提出的基于三維彎曲激波面的變馬赫數乘波體設計方法的靈活性與有效性。

5 結 論

針對常規乘波體氣動布局難以滿足寬域飛行需求的問題，本文將LTOCs 方法與變馬赫數乘波概念相結合，提出了基于三維彎曲激波的變馬赫數乘波體設計方法，借助Bezier 曲面進一步提高了變馬赫數乘波體所“騎乘”激波的選擇自由度。在相同約束條件下，設計了4 個基于三維彎曲激波的變馬赫數乘波體和一個吻切錐變馬赫數乘波體，分析對比了它們在寬域條件下的氣動特性，得到如下結論：

（1）利用LTOCs 方法設計的定馬赫數乘波體可在設計狀態下精準地復現預設計三維激波形狀，波后高壓氣體被成功限制在乘波體下表面，展現出了極佳的乘波特性。同時，LTOCs 方法求得的無黏氣動力參數與CFD 計算結果也基本一致，誤差均小于0.6%，證明了LTOCs 方法在設計基于三維彎曲激波面的定馬赫數乘波體時的高精確性。

（2）利用LTOCs 方法設計的變馬赫數乘波體在設計馬赫數范圍內同樣表現出良好的乘波特性。變馬赫數乘波體Case 2 和Case 3 的綜合性能介于定馬赫數乘波體Case 1 和Case 4 之間，整體更為均衡，更適合寬速域飛行。這與現有錐導/吻切變馬赫數乘波體基本一致，變馬赫數概念的引入使得乘波體設計性能邊界擴大，拓寬了現有乘波體的設計自由度。

（3）各流面內設計馬赫數的離散單調性對此類變馬赫數體的綜合性能有顯著影響，可通過改變設計馬赫數離散分布進行按需設計。單調線性遞減的變馬赫數乘波體Case 2 擁有更小的容積、更弱的壓縮效率、更大的升阻比以及更靠后的壓心位置。此外，變馬赫數乘波體的升阻比與容積之間同樣存在矛盾，設計時需要折中考慮。

（4）吻切錐變馬赫數乘波體對應的三維激波面同樣也屬于掃掠曲面，極大限制了變馬赫數乘波體的設計自由度。相比之下，基于三維彎曲激波的變馬赫數乘波體設計方法借助于Bezier 曲面直接指定三維激波形狀，使得激波的選取更為靈活。相同約束下，Case 2 相較于Case 5 擁有更大的容積與更高的升阻比，但容積率有所下降，馬赫12 時升阻比增加約13.36%。