多胞局域共振型超材料的減振實驗研究

吳 昆，高玉強，王立峰，金棟平，胡海巖

（南京航空航天大學機械結構力學及控制國家重點實驗室, 南京 210016）

彈性波/聲波超材料［1-5］是通過微結構設計實現波動調控并滿足相應波動功能的人工材料和復合結構，其研究涉及波動與振動控制［3，6-7］、智能結構設計［8］和先進成型制造［9］等諸多方向，已受到廣泛關注。在振動控制領域，傳統的隔振裝置和減振技術對中頻振動展現出良好的控制效果，但在低頻區間往往需要較大的安裝空間或較復雜的結構設計才能達到所需振動抑制效果［10］。近年來，人們將基于局域共振機理的彈性波超材料設計為一種減振裝置［11-13］，通過彈性波的調控和傳播衰減，實現對振動能量的抑制隔離。

21 世紀初，Liu 等將局域共振機制［14-15］引入到聲子晶體設計中。該研究相比于傳統的Bragg 散射機制，可在同等幾何尺寸下實現更低頻波動帶隙。Milton 和Wills［16］提 出 了 一 種 簡 潔 的、可 實 現負等效動態質量的物理模型。彈性波在元胞之間傳遞時會將振動能量轉移到內、外質量上，而當元胞的內質量塊發生共振時，外質量振動幅值較小，傳遞到相鄰元胞的機械能降低，波動傳遞一定空間距離后很快衰減，彈性波被阻斷。文獻［17］對Milton 等提出的物理模型開展實驗研究，直觀地演示了超材料在低頻帶隙區間對彈性波的阻斷效應。肖勇等［18-19］在桿、梁和板等固體結構中引入局域共振模塊，基于多帶隙耦合對彈性波帶隙和減振頻帶進行拓寬。文獻［20-21］設計準零剛度超材料構型，通過結構參數的變化來實現和調節低頻帶隙區間。Zhu 等［22］設計含多個局域共振模塊的手性超材料梁模型，通過實驗構型設計和測試研究了寬頻帶隙區間內的振動衰減。Pai 等［23-24］建立了含局域共振子系統的超材料梁、板模型，通過頻散分析和有限元模擬研究了超材料波動帶隙區間的振動抑制效果。Inman 等［25-26］通過參數優化方法對超材料模型進行參數調節，達到增強彈性波阻斷性能和提高振動抑制效果的目標。Matlack 等［27］利用3D 打印技術設計加工了一種立方體晶格超材料模型，在實驗上實現彈性波低頻寬帶頻率區間的波動衰減；Hu 等［28］通過引入梯度構型設計，在超材料梁結構中實現比周期構型更寬頻的振動抑制性能。

然而，將超材料應用到工程振動控制的工作仍然有待進一步研究。本文基于大型可展開空間結構的動力學應用背景［29］，以經典多胞周期超材料為例，設計基于局域共振超材料的減振裝置，實驗測試其對空間桁架構的振動抑制效果。

1 多胞周期超材料的波動分析

本節基于頻散分析給出波動頻率與波矢的關系，研究彈性波在周期結構中傳播特性。圖1 為多胞周期超材料模型，在波傳播方向上將元胞周期性排列。紅色虛框內為一個元胞，元胞的外部質量為M，內部質量為m。在元胞內，連接內、外質量的彈簧和阻尼器的系數分別為k1和c1。同時，連接相鄰元胞的彈簧和阻尼器的系數分別為k0和c0。

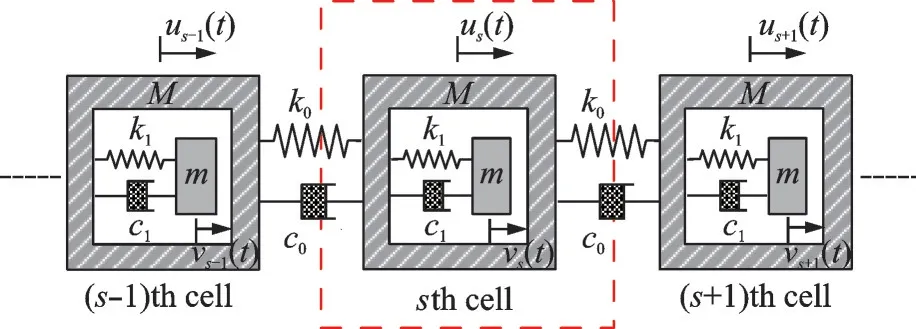
圖1 一維多胞周期超材料模型Fig.1 Model of one-dimensional periodic multi-cell metamaterial

1.1 局域共振元胞的頻散分析

當簡諧形式的彈性波在超材料中傳播時，將第s個元胞的外部質量和內質量的振動位移分別記為us(t)和vs(t)，可得多胞周期超材料的動力學方程組

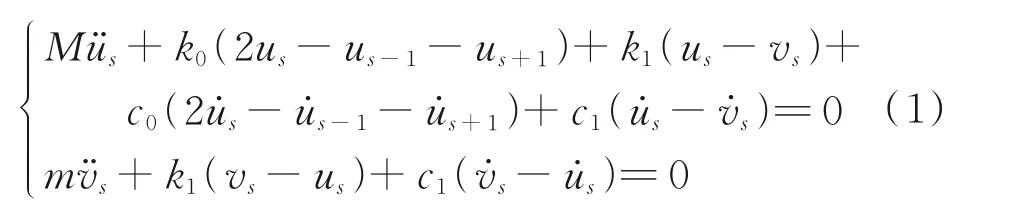
根據Bloch 定理，可假設式（1）的復數形式波動解為

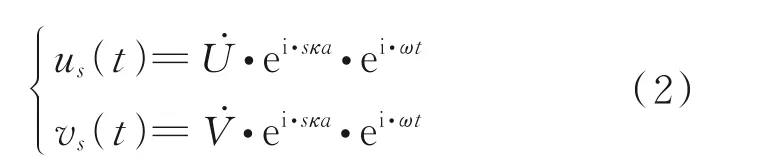
式中：0為零向量；矩陣A和向量Y的具體形式分別為

對式（3）求非零解向量Y，可得如下特征值方程

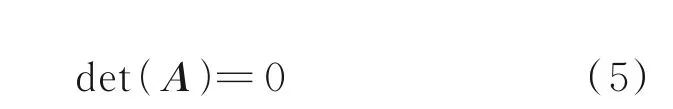
求解式（5）的特征值，即可得到相應的頻散關系。

圖2 給出了量綱為一波動頻率ω˙關于復波數κ的頻散曲線，其中ω˙是將波動頻率ω關于元胞內質量m的無阻尼共振頻率進行了歸一化，即

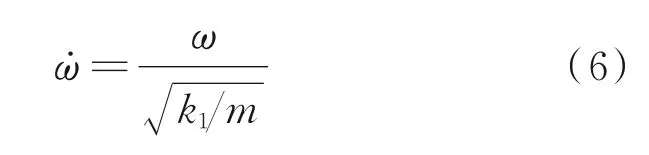
基于表1 給出的超材料結構參數，圖2 陰影區間為頻散分析所得的波動帶隙區。該帶隙分布與局域共振頻率直接相關，并且在共振頻率附近波數虛部更大，反映此頻率段對彈性波有更好的阻斷效果。值得注意的是，對含阻尼耗散的超材料元胞進行頻散分析，代表波動衰減程度的波數虛部大小不僅與所處頻率區間相關，還與超材料模型的阻尼系數相關。

表1 含阻尼超材料分析模型的結構參數Table 1 Structural parameters of damped metamaterials analysis model

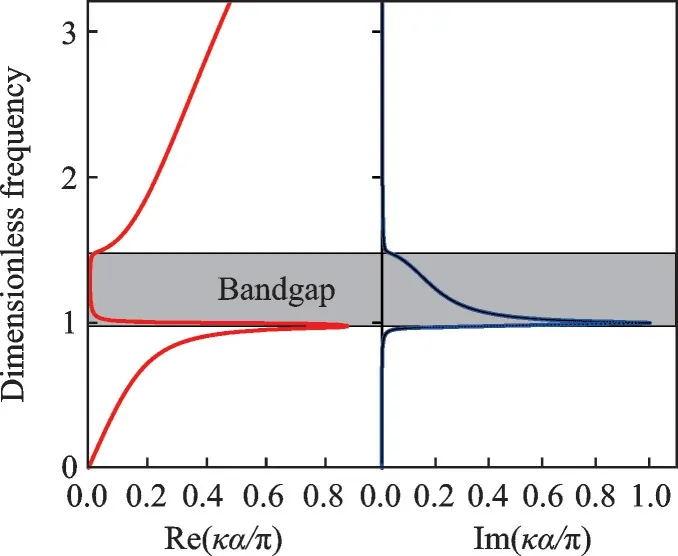
圖2 含阻尼超材料元胞的復頻散曲線Fig.2 Complex dispersion curves of metamaterial unit cell with damping

1.2 多胞周期超材料的波動傳遞率分析

當簡諧行波在周期超材料中傳播時，若不考慮波的反射，則通過計算相鄰元胞的幅值傳遞率可以評估波動傳播情況。對式（1）所示的時域函數進行傅里葉變換，可得頻域方程組

式中頻域復函數Us(ω)和Vs(ω)分別為時域函數us(t)和vs(t)的傅里葉變換。根據超材料的空間周期性和Bloch 波動解形式，可假設

式中：復函數R(ω)與波動頻率相關，而與元胞序號無關。R(ω)的模即為相鄰元胞外質量的振動幅值傳遞率，定義為

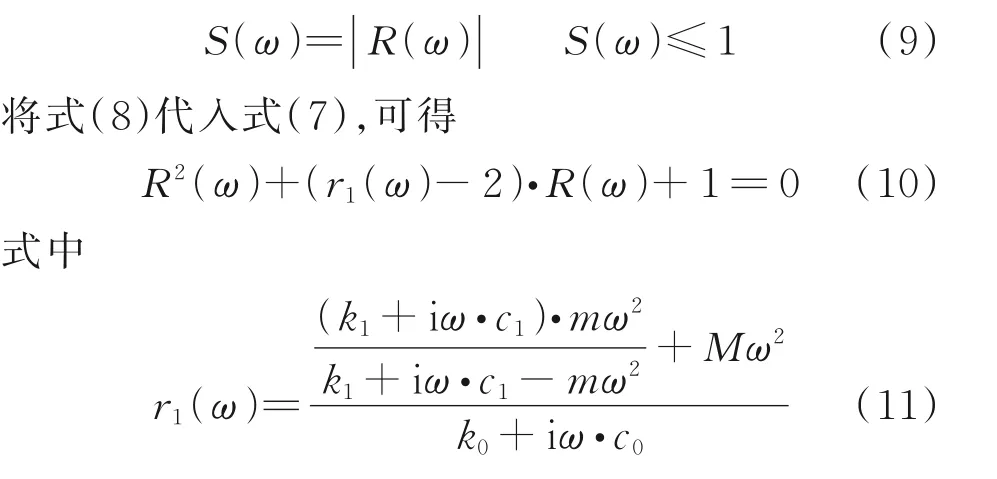
求解式（10），并代入式（9），可得相鄰元胞外質量的波動幅值傳遞率為

基于表1 給出的結構參數，圖3 為單向行波在周期超材料傳播時，相鄰元胞的波動傳遞率頻譜。由圖3 可見，波動傳遞率在陰影區間頻率段大幅降低，反映了彈性波傳播的阻斷效應。此外，該陰影區間頻段與圖2 頻散分析所得的帶隙區間相互吻合。當波動頻率處于帶隙區時，隨著波動傳播距離的增加，周期性超材料元胞的振動幅值呈指數形式迅速衰減。然而，由于傳播介質空間尺寸的限制，彈性波通常會發生反射，因此有必要計算彈性波在有限尺寸的周期超材料中傳播時，超材料各個元胞的振動響應。

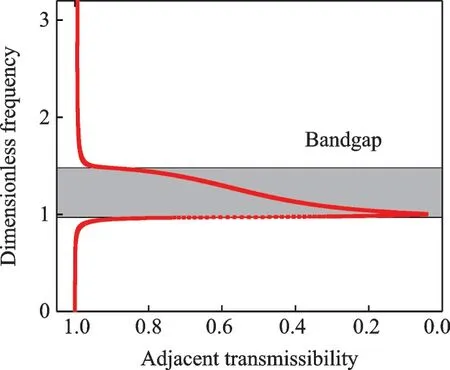
圖3 周期超材料的相鄰元胞波動傳遞率Fig.3 Wave transmissibility of adjacent unit cell in the periodic metamaterial

1.3 有限尺寸多胞超材料的振動響應數值計算

選取一定周期數的有限尺寸局域共振超材料模型，采用數值計算方法研究彈性波在結構中的傳播情況。如圖4 所示，模型左側為位移激勵，時域函數記為u0(t)，連接激勵處為含N個元胞的超材料模型，在遠離激勵方向上依次編號為1，2，…，N，右側連接輸出端，時域響應記為uN+1(t)。

圖4 含有限個單元的一維周期超材料Fig.4 Model of one-dimensional periodic metamaterial with a finite number of unit cells

在 位 移 激 勵u0(t)=u˙0·sinωt下，該 多 自 由 度系統的動力學方程組為

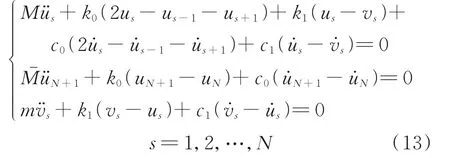
基于表1 的結構參數，選取超材料的元胞個數為N=10，設定兩種輸出端質量分別為M˙=10M和M˙=0.1M，通 過4 階Runge-Kutta 數 值 計 算 方法，可得到不同激勵頻率下輸出端M˙的振動響應，其結果如圖5 所示。定義輸出頻響為質量M˙的位移幅值與激勵位移幅值u˙0之比的對數比例關系，單位為dB，即

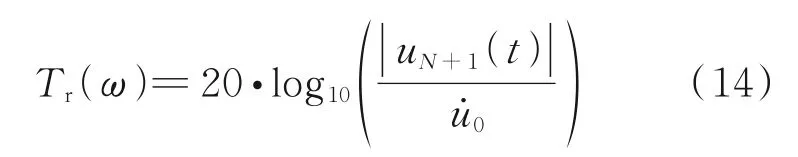
由圖5 可見，在共振頻率附近的帶隙區內，輸出端位移傳遞率遠小于0 dB，反映了該頻段彈性波傳播的阻斷衰減。對比兩種輸出端質量M˙=10M和M˙=0.1M，可發現輸出端質量較大時，高頻段的波動響應傳遞率更小，其原因是此時末端質量M˙的振動響應更不容易被激發。

圖5 有限尺寸的周期超材料輸出端波動傳遞率Fig.5 Wave transmissibility of response in a finite periodic metamaterial

2 空間桁架結構的振動抑制應用

2.1 多胞周期超材料的實驗構型設計

參照圖4 的有限個周期多胞超材料模型，圖6給出對應的結構構型設計和3D 打印成型實驗件。由于空間尺寸限制，多胞超材料實驗件的元胞個數取為N=5。元胞外部質量和結構框架由光敏樹脂一體成型，元胞中間嵌入圓柱體金屬塊充當振子，彈簧和阻尼器的連接模塊通過薄梁的彎曲變形來等效對應的剛度和阻尼系數。表2 給出了多胞超材料實驗裝置的設計結構參數。

圖6 多胞超材料的實驗構型Fig.6 Experimental configuration of a multi-cell metamaterial

表2 減振實驗裝置的設計參數Table 2 Design parameters of experimental facility for vibration attenuation

圖7 給出空間桁架結構減振的實驗裝置，它由帶關節非線性約束的立方體桁架結構、超材料隔振裝置和振動測試設備等組成，主要包括激振器1臺、數據采集系統1 套、功率放大器1 臺、加速度傳感器4 個、桁架懸掛裝置和超材料懸掛裝置各1 個，超材料隔振裝置兩端分別連接激振器和立方體桁架。其中空間桁架單元由12 根桿件、8 個端點3 向連接關節和4 根面對角扭簧拉索構成，具有輕質高強、結構靈活、宜于展開和收攏等優點。工程中常常將桁架單元沿一個方向或兩個方向周期性延伸或者進行環形分布，結構尺度可達101～102m 量級，所得大型桁架結構的動力學特性十分復雜，具有撓性、低剛度、弱阻尼、頻率低和模態密集等特性［29］。一旦遇到外界擾動，擾動產生的彈性波在整個空間桁架的桿和關節中傳播并且衰減緩慢，對航天器定位和結構穩定性帶來嚴重影響。對于沿一個方向延拓的空間周期桁架，多個面外和面內振動頻率分布密集，從1 赫茲到幾十赫茲不等，與選取的桁架周期數以及扭簧調節預緊力有關；對于環形桁架結構［30］，前幾階徑向振動的頻率分布從0.6～30 Hz。值得注意的是，為了在有限空間內實現桁架單元的低頻振動抑制，同時縮小減振裝置的尺寸，將超材料元胞內部的薄梁采用Z 型折疊設計，以降低等效的彈簧剛度和元胞的局域共振頻率。空間桁架單元的質量為3.0 kg，3D 打印的多胞周期超材料框架質量約為0.148 kg，在不明顯增加結構附加質量的前提下，對受擾動的空間桁架結構在5～60 Hz 頻率區間進行減振實驗測試。

圖7 減振應用實驗裝置Fig.7 Experiment setup for vibration attenuation

如圖7 左圖所示，在空間桁架遠端安裝3 個加速度傳感器，用于測量X-Y-Z這3 方向的加速度振動響應。空間桁架和超材料減振裝置分別用柔性繩索和橡皮筋懸掛并保持水平，再將激振器、多胞超材料和空間桁架固定連接并保持在同一水平面。整體實驗裝置在激勵前達到靜態平衡，從而可忽略重力對結構振動的影響。除結構阻尼外，還忽略了其他摩擦阻尼的影響。設置激振器輸入激勵信號為正弦形式，激勵方向為X方向，采用固定激勵頻率和慢速掃頻兩種激發方式，由彈性波通過超材料傳遞到空間桁架，引起其遠端關節的振動響應。在激勵位置和桁架遠端關節3 方向上，采集各自的加速度信號，分別得到輸入激勵和輸出響應的時域歷程，對時域信號處理后獲得加速度傳輸率頻譜。

2.2 空間桁架振動抑制的實驗結果

首先，采用定頻正弦位移激勵，分別選取5 Hz和17.5 Hz 兩個頻率點，記錄立方體桁架的3 向加速度時間響應，其結果如圖8 所示。由圖8 可見，在頻率5 Hz 的正弦激勵下，X方向的振動能量通過彈性波傳遞到柔性空間桁架后，在X、Y、Z這3 個方向上均引起桁架的結構振動，振動能量也因此分配在3 個方向上。作為對比，當激振器施加頻率17.5 Hz 的正弦激勵時，空間桁架遠端關節3 方向的振動幅值幾乎可以忽略。這表明，此時彈性波難以傳播到空間桁架上。

圖8 空間桁架的XYZ 方向加速度時域響應Fig.8 Three-dimensional accelerations of the space truss in time domain under excitations

之后采用掃頻激勵方式，設定頻率區間從5～60 Hz，圖9 展示了桁架結構X、Y、Z這3 個方向上的加速度幅值傳輸率。對比3 個方向的振動響應可發現，在較高頻率區間X方向的振動幅值遠大于另外兩個方向，其原因在于X方向為施加激勵的方向。在15～45 Hz 頻率區間，空間桁架的加速度相比于其他頻率段有明顯降低，表明振動能量傳遞到空間桁架受到較明顯阻斷。綜合3 個方向的加速度幅值，可得全加速度傳遞率頻譜，其結果如圖10所示。從圖10 可見，從5～60 Hz 的整個低頻區間，空間桁架的振動響應均得到一定程度的抑制。特別地，在帶隙區間15～45 Hz 段，桁架的振動響應傳遞率低于-30 dB，并且最大衰減程度可達近-40 dB。這表明，所設計的超材料裝置在低頻區間具備良好的波動阻斷效果，可達到空間桁架振動抑制的應用目標。

圖9 空間桁架XYZ 方向的加速度傳輸率頻譜Fig.9 Transmissibility spectrum of three-dimensional accelerations of the space truss

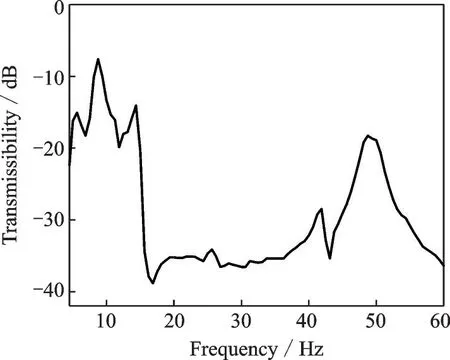
圖10 空間桁架全加速度的傳遞率頻譜Fig.10 Transmissibility spectrum of total accelerations of space truss

3 結 論

本文針對空間桁架結構的減振需求，基于對局域共振型周期超材料的波動分析，設計了一種較為輕質的多胞超材料實驗件構型，可在15～45 Hz 的頻率區間內降低空間桁架的振動幅值達30 dB，部分頻段衰減可達近40 dB。實驗表明，在不明顯增加附加質量和安裝空間的前提下，多胞周期超材料對立方體柔性桁架展現出良好的減振應用效果。