愛爾特希點集

文／于弢整理

數學小故事

匈牙利數學家愛爾特希（P．Erdos，1913-1996）提出過這樣一個問題：在平面內有n個點，任意三個點都能構成等腰三角形，這樣的點集存在嗎？

數學家們的研究成果如下：

當n=3時，是顯然存在的。

當n=4時，有且僅有三種結構：任一等腰三角形的三個頂點及它的外心（注：“外心”是指三角形三邊垂直平分線的交點）；任一菱形（注：“菱形”是四邊相等的四邊形）的四個頂點；正五邊形的任意四個頂點。

我們來簡單解釋一下。第一種結構如圖1，在△ABC中，AB=AC，D為△ABC的外心。因為D為△ABC的外心，所以BD=AD=CD。取A、B、C、D四點中的任意三點可構成4個三角形，分別為△ABC、△ABD、△ACD、△BDC，均為等腰三角形。第二種結構如圖2，易于理解，不再贅述。第三種結構如圖3，A、B、C、D、E是正五邊形的5個頂點，取其中任意4個頂點，如點A、B、C、D，可證明△ABC、△ABD、△ACD、△BDC均為等腰三角形。

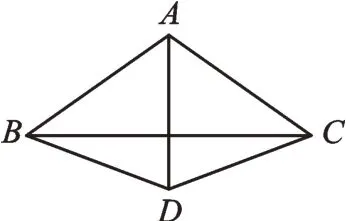
圖1

圖2

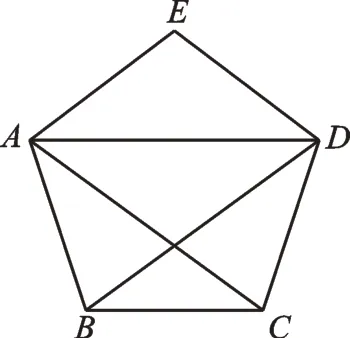
圖3

當n=5和n=6時，也可以找到滿足條件的點集。但當n≥7時，這樣的點集便不存在了。人們將具有這樣性質的n個點構成的點集稱為愛爾特希點集。

同學們，你能畫出n=5時的愛爾特希點集嗎？試一試吧。