鴨翼位置對二元機翼靜氣彈特性的影響

王 振,蘇新兵,王 寧,馬斌麟

(1.空軍工程大學 航空工程學院， 西安 710038； 2.空軍工程大學 航空機務士官學校，河南 信陽 464000)

1 引言

現代飛行器結構柔性越來越大，在對機翼氣動參數優化過程中，就必須要考慮到彈性變形影響。近年來隨著復合材料的應用，柔性機翼的設計理念越來越受重視。目前已有許多對鴨式布局的研究，鴨翼面產生的渦系能對主翼渦產生有利干擾，控制主機翼表面附面層分離，使主機翼的失速迎角和最大升力系數明顯增大。空軍工程大學的張冬等通過對比單獨鴨翼渦以及前、后掠翼布局中鴨翼渦與機翼前緣渦的干擾分析了鴨翼渦流動機理，文獻[4]中通過數值模擬研究了鴨翼對翼身融合布局飛機低速縱向氣動特性的影響，北京航空航天大學的陳慶民等也對非定常運動中鴨翼高度對戰機縱向氣動特性的影響進行了揭示。這些研究基本集中于剛性機翼方面，關于鴨翼對柔性機翼靜氣彈特性影響的研究十分有限。

對機翼性能的研究必須先從翼型氣動特性和彈性變形特性開始進而延伸到三維有限翼展的研究，因此本文中以NACA64A010翼型為基準，采用CFD/CSD松耦合數值仿真計算方法，研究亞音速條件下鴨翼位置對二元翼型氣動特性和彈性變形特性的影響，為進一步研究鴨翼對前掠機翼靜氣動彈性發散特性的影響提供參考。

2 計算方法及驗證

本研究在處理二維翼型計算問題中采用基于CFD/CSD松耦合的靜氣動彈性計算方法。松耦合方法即分離解法，其不需要耦合流、固控制方程，而是按設定順序在同一求解器或不同求解器中分別求解流體控制方程和固體控制方程，通過流固交界面(FS Interface)把流體域和固體域的計算結果互相交換傳遞,待此時刻收斂達到要求，進行下一時刻的計算，依次而行求得最終結果。在每一次迭代過程中，采用常體積轉換(constant volume transformation，CVT)方法進行氣動力與結構位移插值傳遞。流體域將氣動力傳遞給固體域完成相應靜力學計算后，產生的結構位移導致流體域網格質量變差，再采用徑向基函數方法對流體域網格進行更新優化，以滿足下一次迭代求解的要求。

流場計算是耦合計算的重點，CFD求解器采用Navier-Stokes(N-S)方程作為描述流體運動控制方程，根據Einstein求和約定，在笛卡爾坐標系中，不考慮熱源的N-S方程積分守恒形式可表達為：

(1)

式中：為狀態矢量項；和分別為無粘和粘性通矢量項；為控制體；表示控制體表面；為表面微元外法向向量。

因為平均N-S方程的不封閉性，需要引入湍流模型來封閉方程組，本文采用穩定、收斂性良好且適用于低雷諾數條件的Spalart-Allmaras(S-A)模型。流體控制方程的離散采用有限體積法，在結構域計算中，針對本文所研究的二元翼型靜氣彈特性問題只關心響應結果而不關心響應過程的特點，借助結構靜力學便可滿足本文靜氣彈特性分析需求。固體控制方程的離散則采用有限元方法。

為了驗證二元翼型計算方法的準確性，本文使用NACA0012翼型的二維靜氣動彈性特性算例對所采用數值計算方法的有效性和精度進行驗證,分別對流體域與結構域進行網格劃分，流體域多邊形網格單元數為18 527，結構域三角形網格單元數為4 163，劃分后的網格如圖1。

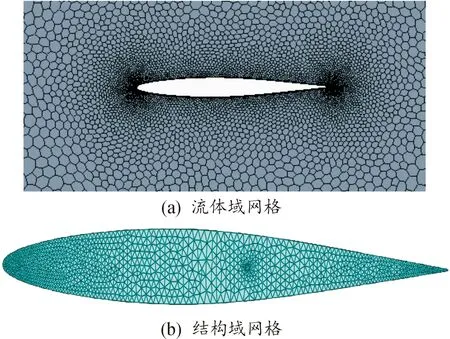
圖1 NACA64A010翼型靜氣彈模型網格示意圖Fig.1 The mesh used in static aeroelastic computation of NACA64A010 airfoil

在仿真計算中，流場計算條件為：=015，=6×10，=293.15 K。其中鴨翼為剛性，主翼為彈性，主翼機翼屬性為=108 GPa，=0.33，=4 500 kg/m。其中：為彈性模量；為泊松比；為密度。

通過仿真計算得到NACA0012翼型在0～20°內多個攻角下的升力系數，如圖2所示。對比實驗值與仿真值發現，相同攻角下翼型的升力系數相近，最大誤差小于5%。

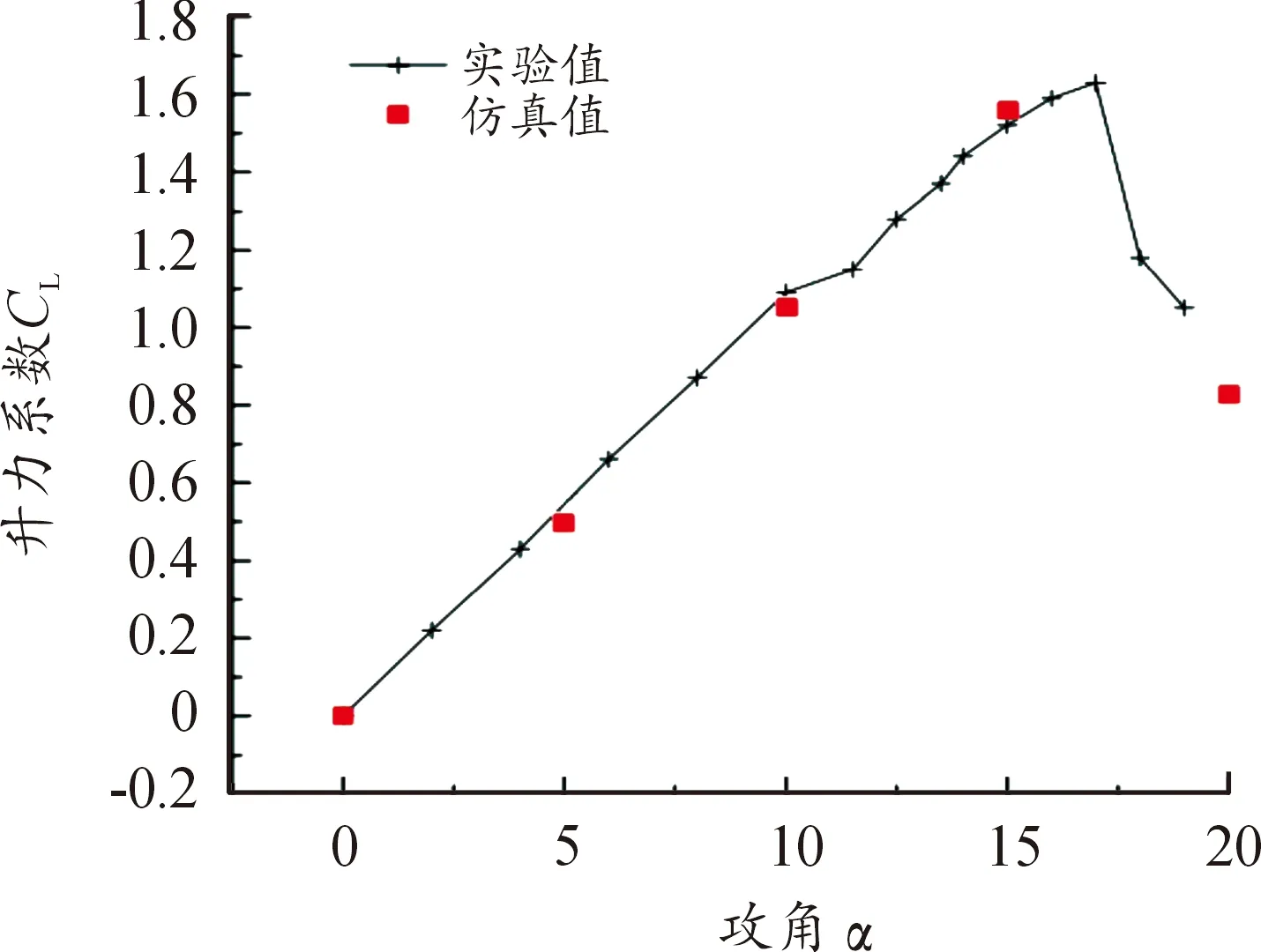
圖2 NACA64A010翼型不同攻角下的升力系數曲線Fig.2 The lift coefficient of NACA64A010 airfoil under different angle of attack

通過多次流固耦合迭代計算，可得到=5°時翼型前緣點和后緣點的位移，將本次數值計算的結果與文獻[10]中二維靜氣彈特性算例得到的翼型前、后緣點位移結果，如表1所示。本次仿真計算的收斂曲線如圖2。

表1 計算結果與算例結果Table 1 The results of calculation compared with those of examples

由圖3可知，迭代超過13000次后，殘差穩定低于收斂精度10，計算收斂。在仿真計算中，計算平臺、湍流模型以及網格劃分的不同都會帶來誤差，但誤差在5%以內，說明選取的仿真方法滿足準確性要求。

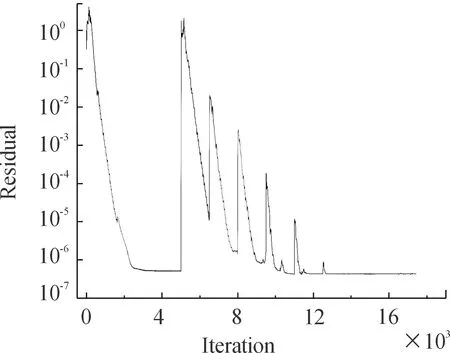
圖3 收斂曲線Fig.3 Residual curve

3 計算模型

本文計算模型選取NACA64A010翼型，模型如圖4所示。

圖4 二元機翼模型示意圖Fig.4 The model of two-demensional wing

模型主翼弦長=10mm，鴨翼弦長=500 mm，主翼剛心取至=055，鴨翼為固支狀態。以主翼前緣點為坐標原點，建立二維坐標系，模型具體計算位置如表2所示。

表2 模型簡況Table 2 Models abbreviation

在計算過程中，固定主翼為彈性狀態，鴨翼為剛性狀態。對流體域進行六邊形網格劃分，對結構域進行三角形網格劃分。選取合適的近壁面第一層網格高度，使值為1左右，遠場邊界到模型的距離為10倍主翼弦長。劃分后網格如圖5所示。

圖5 C-FSW01模型網格示意圖Fig.5 The mesh of C-FSW01 model

4 鴨翼高度影響

在=02,=4.11×10的條件下，對不同鴨翼高度模型的氣動特性和彈性變形特性參數進行仿真計算，如圖6所示。

4.1 氣動特性

由圖6(a)可知，無論是剛性狀態還是彈性狀態，3種模型的失速迎角均為=10°，3種模型升力系數隨迎角的變化趨勢類似，但彈性狀態下升力線斜率要比剛性狀態下的大。鴨翼高度不同，升力系數呈現顯著差異，C-FSW02模型升力系數最高，彈性狀態下max≈1.42，比C-FSW01模型高45.4%。這是由鴨翼擾流作用引起的，當鴨翼位于主機翼正前方時，其擾流作用最明顯，破壞了主機翼的渦系，導致升力系數下降；當鴨翼位于主機翼上方時，鴨翼產生的旋渦對主機翼氣流分離起到有利干擾，使升力系數增加。

由圖6(b)可知，阻力系數隨迎角不斷增加，當<10°時，阻力系數隨迎角增加而緩慢增加，因為此時機翼表面氣流未分離，渦系結構未被破壞，阻力較小。當>10°時，阻力系數隨迎角急劇增加，此時機翼表面氣流分離嚴重；其中彈性機翼阻力系數比剛性機翼的大，且隨迎角增大，彈性機翼阻力系數增量略有增加；鴨翼高度不同，阻力系數表現出明顯差異，C-FSW02模型阻力系數較C-FSW03模型的小，說明高位鴨翼與主機翼相互耦合對氣動性能起到了改善作用。

由圖6(c)可知，不同鴨翼高度對最大升阻比影響顯著，其中，高位鴨翼升阻特性最好，C-FSW02模型和C-FSW03模型均在=6°時獲得最大升阻比，且最大升阻比均較C-FSW01模型高出125%。不同模型小迎角狀態下，彈性條件下升阻特性均比剛性條件下的好，當>6°時，剛性條件下升阻特性更好，說明在>6°條件下，機翼的彈性變形已經破壞了機翼表面渦流。在α<12°范圍內，高位鴨翼升阻特性最好，而大迎角時提升作用很小。

圖6 不同鴨翼高度模型氣動特性參數曲線Fig.6 Aerodynamic characteristics of models with different canard position in vertical direction

4.2 彈性變形特性

不同鴨翼高度對翼型氣動特性產生明顯影響，翼型表面氣動力變化會引起其彈性變形的變化。本節對比了3種鴨翼模型的彈性變形情況，定義為前緣向撓度，彎曲變形量為前、后緣向的位移之和。

由圖7可知，C-FSW01模型彈性變形近似為0，這是由其較小的氣動力決定的，對于C-FSW02模型，前緣向撓度和彎度的變化趨勢均為先增大后減小，當=10°時，和均達到最大值，此時max=14.134 23，max=2.857 95。對于C-FSW03模型，其前緣撓度和彎度變化趨勢與C-FSW02模型相近，其和均略低于C-FSW03模型，且分別減少了約4.71%和4.56%。

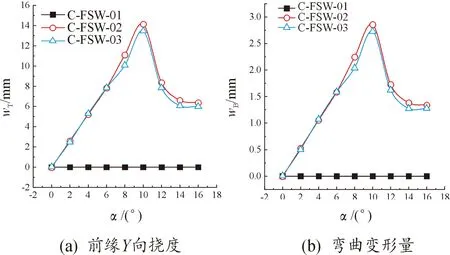
圖7 主翼面彈性變形量曲線Fig.7 The elastic deformation characteristics of wing

4.3 流動機理分析

分別比較不同迎角狀態下C-FSW01模型彈性狀態機翼表面流線圖，如圖8。

圖8 C-FSW01模型不同迎角時的流線圖Fig.8 The streamline of C-FSW01 model with different angle of attack

小迎角條件下，鴨翼和主翼翼面流動表現為附著流態，未出現明顯漩渦，因此升力系數曲線為線性變化，彈性變形量和線性增加，由于鴨翼失速迎角較小，同時主翼對鴨翼的上洗作用加快了鴨翼表面氣流分離，鴨翼上表面附著渦首先發生破裂，漩渦卷積但未破裂，主翼表面仍為附著流態，這就導致中等迎角情況下，升力系數非線性增加，當=10°時，主翼仍保持為附著流態，此時升力系數和彈性變形量均達到最大；隨著迎角增加，主翼上表面旋渦破裂，流速變慢，導致主翼升力系數下降，彈性變形量也下降。

當=6°時，彈性條件下C-FSW01、C-FSW02和C-FSW03模型的流線圖如圖9。

圖9 α = 6°時模型的流線圖Fig.9 The streamline of different models when α = 6°

由圖9可知，在低馬赫數、小迎角條件下，3種翼型均未出現明顯氣流分離，未出現明顯旋渦，所以鴨翼對主翼的影響主要表現為擾流作用。鴨翼后緣流速出現明顯下降，其中C-FSW01模型受到的影響最大，導致主翼上表面氣流流速降低。C-FSW02模型中鴨翼對主翼產生的影響最小。

C-FSW01、C-FSW02和C-FSW03模型的壓力云圖如圖10。由此可知，3種模型表面壓力狀況沒有顯著差異，主要因為低亞音速，小迎角條件下翼型表面氣流處于附著流態。主翼上表面壓力差距不大。但下表面略有差異，C-FSW02和C-FSW03模型相比，下表面壓力較大，主要是因為C-FSW03模型鴨翼上表面高速氣流繞過主翼下表面，使得主翼下表面壓力降低，使得高位鴨翼模型升力特性優于低位鴨翼模型。

圖10 α = 6°時模型的壓力云圖Fig.10 The pressure contour of different models when α = 6°

當=12°時，彈性條件下C-FSW01、C-FSW02和C-FSW03模型的流線圖和壓力云圖如圖11和圖12。

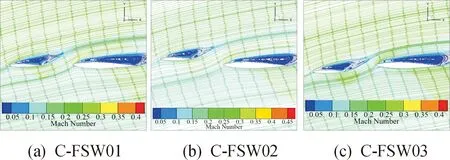
圖11 α = 12°時模型的流線圖Fig.11 The streamline of different models when α = 12°

由圖11可知，當=12°時，3種模型翼型表面均出現明顯渦流，相比C-FSW01和C-FSW03模型，C-FSW02模型主翼渦與鴨翼渦產生有利干擾，鴨翼渦對主翼下洗作用明顯，加快了主翼表面流速，同時，鴨翼渦對主翼渦產生一定的后推作用。

由圖12可以看出，鴨翼渦的作用主要體現在了主翼上表面前端，C-FSW02模型主翼上表面壓力系數明顯較低，同時高位鴨翼上表面壓力系數也較低，從而提供了一部分升力。

圖12 α = 12°時模型的壓力云圖Fig.12 The pressure contour of different models when α = 12°

5 鴨翼距離影響

5.1 氣動特性

為了進一步研究鴨翼位置對主翼靜氣彈特性的影響，在=02,=4.11×10的條件下，分別計算了不同鴨翼距離的升、阻力系數、升阻比以及俯仰力矩系數，如圖13所示。

由圖13(a)可知，相比較于近距鴨翼，遠距鴨翼對升力系數有明顯的改善作用。彈性狀態下，C-FSW04模型和C-FSW05模型升力系數分別比C-FSW01模型的增大約42.89%和45.13%，且遠距鴨翼達到升力系數最大值時，有一個較為明顯的升力系數平臺，提升了機翼的失速特性，且距離越大，平臺越大，對于C-FSW04模型，平臺范圍為8°～10°，對于C-FSW05模型，平臺范圍為8°～12°。這是因為，鴨翼與主機翼位于同一水平高度，鴨翼位置越近，鴨翼渦對主機翼擾流作用越明顯，導致大迎角時主機翼表面渦流結構完全破壞，升力系數下降。

由圖13(c)可知，相較于近距鴨翼，遠距鴨翼升阻特性更好，其中C-FSW04模型和C-FSW05模型最大升阻比分別比C-FSW01模型的高出約126.40%和127.76%。其中，彈性狀態下升阻特性相較于剛性狀態下更優。

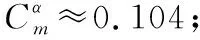
圖13 不同鴨翼距離模型氣動特性參數曲線Fig.13 Aerodynamic characteristics of models with different canard position in horizontal direction

5.2 彈性變形特性

由圖14可知，不同鴨翼距離情況下，當迎角變化時，主翼變形情況略有不同。當<10°時，C-FSW04模型和C-FSW05模型和均線性增加。當>10°時，C-FSW04模型和非線性逐漸減小；C-FSW05模型和先增大后減小。當=10°時，C-FSW04模型max=14.886 32，max=3008 86；當=12°時，C-FSW04模型彈性變形量達到最大，分別提高約3.25%和4.13%。

圖14 主翼面彈性變形量曲線Fig.14 The elastic deformation characteristics of wing

5.3 流動機理分析

當=6°時，彈性條件下C-FSW01、C-FSW04和C-FSW05模型的流線圖和壓力云圖如圖15和圖16所示。

圖15 α = 6°時模型的流線圖Fig.15 The streamline of different models when α = 6°

圖16 α=6°時模型的壓力云圖Fig.16 The pressure contour of different models when α = 6°

由圖15可知，在低馬赫數、小迎角狀態下，3種翼型均未出現明顯氣流分離，所以鴨翼對主翼的影響主要表現為擾流作用。由圖16看出，3種模型表面壓力差異不大。鴨翼與主翼距離增大，兩者相互影響變小。遠距鴨翼對主翼面的擾流作用減小，使遠距鴨翼前緣上翼面流速更大，相較于其他模型氣動特性更好。

當=12°時，彈性條件下C-FSW01、C-FSW04和C-FSW05模型的流線圖和壓力云圖如圖17和圖18所示。

圖17 α = 12°時模型的流線圖Fig.17 The streamline of different models when α = 12°

圖18 α = 12°時模型的壓力云圖Fig.18 The pressure contour of different models when α = 12°

由圖17和圖18可知，當=12°時，3種模型翼型表面均出現明顯的氣流分離，上表面卷繞形成渦流，相比較于近距鴨翼模型，遠距模型渦流明顯減小。近距鴨翼主翼渦流與鴨翼渦的干擾作用明顯，鴨翼渦對主翼渦的下洗作用導致主翼上表面氣流提前分離，渦核破裂，上表面吸力減小主翼升力貢獻減小，而主翼渦對鴨翼的上洗作用也減少了鴨翼有效迎角，延緩了鴨翼氣流的過早分離，鴨翼上表面吸力增大，鴨翼升力貢獻增大，但由于主翼是升力主要產生部件，所以遠距鴨翼氣動特性較好。

對于近距鴨翼模型，由于主翼渦形成較早，主翼渦翻卷較為嚴重，導致主翼上表面渦流不斷向機翼前源擴散，旋渦區域氣流流速下降，吸力減小，主要升力部件向前緣靠攏，由于主機翼剛心=055，所以氣動中心與剛心距離逐漸變大，導致近距鴨翼升力分布變差，在上表面旋渦未覆蓋整個上表面區域前(α<10°)，近距鴨翼模型彈性變形反而變大，同樣壓力貢獻下比遠距鴨翼模型變形量大。

6 結論

1) 不同鴨翼高度模型中，高位鴨翼氣動性能最好，彈性條件下，C-FSW02模型升力系數比C-FSW01模型高45.4%，最大升阻比比C-FSW01模型高125%，彈性變形特性3種模型近似；

2) 不同鴨翼距離模型中，遠距鴨翼氣動特性和彈性變形特性更好，C-FSW04模型和C-FSW05模型分別比C-FSW01模型升力系數增大約42.89%和45.13%。遠距鴨翼達到升力系數最大值時，有一個較為明顯的升力系數平臺，且高升力系數帶來的彈性變形增量較小。

本文中的仿真結果表明，當=02,=411×10時，高位、遠距鴨翼會改善主翼面氣動特性，延緩彈性變形。仿真結果可為后續研究三維鴨翼對前掠翼靜氣動彈性發散特性的影響提供參考。